五年级下册数学课件-6.3 方程与代数 沪教版 12张PPT
文档属性
| 名称 | 五年级下册数学课件-6.3 方程与代数 沪教版 12张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 112.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 12:26:34 | ||
图片预览





文档简介
简易方程复习
教学目标:
1、知识目标:会解学过的方程和列方程解决问题。
3、情感目标:养成检查和验算的习惯。
2、能力目标:能正确解方程及相关的文字题和应用题。
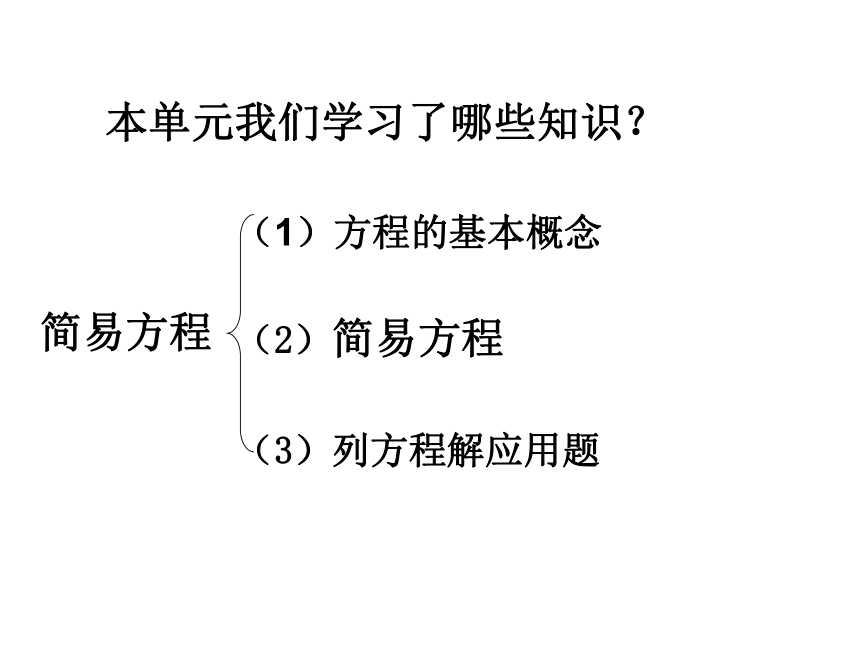
本单元我们学习了哪些知识?
简易方程
(1)方程的基本概念
(2)简易方程
(3)列方程解应用题
例1:下列式子中,属于方程的有( )
A)10+8=6×3 B)8X+0.4×5=10
C)t-6>s+7 D)ma÷b
练习1:解方程并验算:8X+0.4×5=10
(1)含有 的 叫做方程。
(2)使方程左右两边 的未知数的值,叫做方程的解。
(3)求 过程叫做解方程。
练习2:填空:
练习3:思考题:
已知方程 8X+0.4×5=10 与方程 7-4X = M
的解相等,求: M = ?
例2:列方程解应用题
学校合唱队、舞蹈队共有84人,已知合唱队比
舞蹈队的3倍多4人。求:舞蹈队、合唱队人数。
等量关系:
合唱队人数+舞蹈队人数=84人
(4)检验:写出答案。
(1)审题:弄清题意,找出未知数,并用x表示;
(2)分析:找出题中数量之间的等量关系,列方程;
列方程解解决问题的基本步骤:
(3)计算:解方程;
练习4:说出下面各题中数量之间的相等关系。
(1)养禽场一共养鸡鸭600只。
(2)红花比黄花少25朵。
(3)参加航模组的人数是参加美术组的3倍。
(4)小胖体重比小巧的1.2倍还多8千克。
鸡的只数+鸭的只数=600只
黄花的数量-红花的数量=25朵
参加美术组的人数×3=参加航母组的人数
小胖体重 - 小巧体重×1.2 = 8
(1)一块梯形草坪的面积是30平方米,高6米,已知下底是上底的1.5倍。求梯形下底长多少米?
练习5
列方程解应用题
(2)两个城市相距255千米,甲乙两车同时从两个城市出发相向而行,甲车速度为48千米/时。2.5小时后两车相遇,乙车的速度是多少?
练习5
列方程解应用题
(3)发糖,如果每个同学发8颗,则少了32颗;若如果每个同学发6颗,则多了16颗,问:班级中一共有几个学生?一共准备了几颗糖?
练习6
列方程解应用题
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
每人发糖
班级人数
糖的总数
方案一
方案二
本课小结
通过今天的复习,你有什么收获?
简易方程
含有的未知数的等式叫做方程;
使方程左右两边相等的未知数的值;
求方程解的过程叫做解方程;
1、弄清题意,用X表示未知量;
2、分析关键句,找等量关系,列方程;
3、解方程并检验作答。
教学目标:
1、知识目标:会解学过的方程和列方程解决问题。
3、情感目标:养成检查和验算的习惯。
2、能力目标:能正确解方程及相关的文字题和应用题。
本单元我们学习了哪些知识?
简易方程
(1)方程的基本概念
(2)简易方程
(3)列方程解应用题
例1:下列式子中,属于方程的有( )
A)10+8=6×3 B)8X+0.4×5=10
C)t-6>s+7 D)ma÷b
练习1:解方程并验算:8X+0.4×5=10
(1)含有 的 叫做方程。
(2)使方程左右两边 的未知数的值,叫做方程的解。
(3)求 过程叫做解方程。
练习2:填空:
练习3:思考题:
已知方程 8X+0.4×5=10 与方程 7-4X = M
的解相等,求: M = ?
例2:列方程解应用题
学校合唱队、舞蹈队共有84人,已知合唱队比
舞蹈队的3倍多4人。求:舞蹈队、合唱队人数。
等量关系:
合唱队人数+舞蹈队人数=84人
(4)检验:写出答案。
(1)审题:弄清题意,找出未知数,并用x表示;
(2)分析:找出题中数量之间的等量关系,列方程;
列方程解解决问题的基本步骤:
(3)计算:解方程;
练习4:说出下面各题中数量之间的相等关系。
(1)养禽场一共养鸡鸭600只。
(2)红花比黄花少25朵。
(3)参加航模组的人数是参加美术组的3倍。
(4)小胖体重比小巧的1.2倍还多8千克。
鸡的只数+鸭的只数=600只
黄花的数量-红花的数量=25朵
参加美术组的人数×3=参加航母组的人数
小胖体重 - 小巧体重×1.2 = 8
(1)一块梯形草坪的面积是30平方米,高6米,已知下底是上底的1.5倍。求梯形下底长多少米?
练习5
列方程解应用题
(2)两个城市相距255千米,甲乙两车同时从两个城市出发相向而行,甲车速度为48千米/时。2.5小时后两车相遇,乙车的速度是多少?
练习5
列方程解应用题
(3)发糖,如果每个同学发8颗,则少了32颗;若如果每个同学发6颗,则多了16颗,问:班级中一共有几个学生?一共准备了几颗糖?
练习6
列方程解应用题
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
每人发糖
班级人数
糖的总数
方案一
方案二
本课小结
通过今天的复习,你有什么收获?
简易方程
含有的未知数的等式叫做方程;
使方程左右两边相等的未知数的值;
求方程解的过程叫做解方程;
1、弄清题意,用X表示未知量;
2、分析关键句,找等量关系,列方程;
3、解方程并检验作答。
