四年级下册数学课件 第八单元“智慧广场” 青岛版(五四学制)(21页PPT)
文档属性
| 名称 | 四年级下册数学课件 第八单元“智慧广场” 青岛版(五四学制)(21页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 00:00:00 | ||
图片预览




文档简介
青岛版五四制小学数学 四年级下册
智慧广场——排列问题
学习准备:
1.准备好笔和练习本。
3.学习过程中,根据老师的提示,及时按下暂停键,进行问题思考、动手操作和练习等活动。
请按下暂停键
2.准备好写有小冬、小华、小平的学具卡片若干张。
小冬
小华
小平
学习目标
1.在解决问题的过程中,初步发现简单排列现象中的规律,能运用规律解决一些简单的实际问题。
2.在学习中能感知解决问题策略的多样性。
3.感受数学在现实生活中的广泛应用,感受数学的价值。
情境导入
从图中,你知道了哪些数学信息?
小冬、小华、小平3个同学排成一行照相。
有多少种不同的排法?
小冬
小华
小平
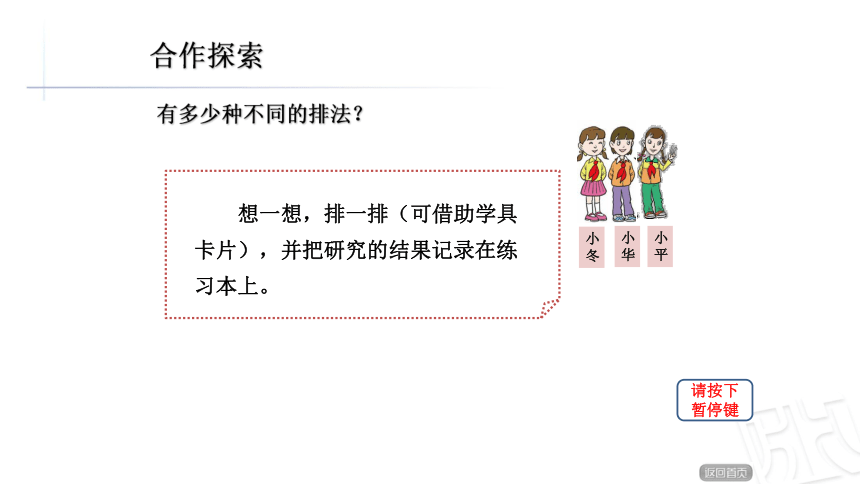
合作探索
有多少种不同的排法?
小冬
想一想,排一排(可借助学具卡片),并把研究的结果记录在练习本上。
小华
小平
请按下暂停键
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小冬
小平
小华
①
②
③
④
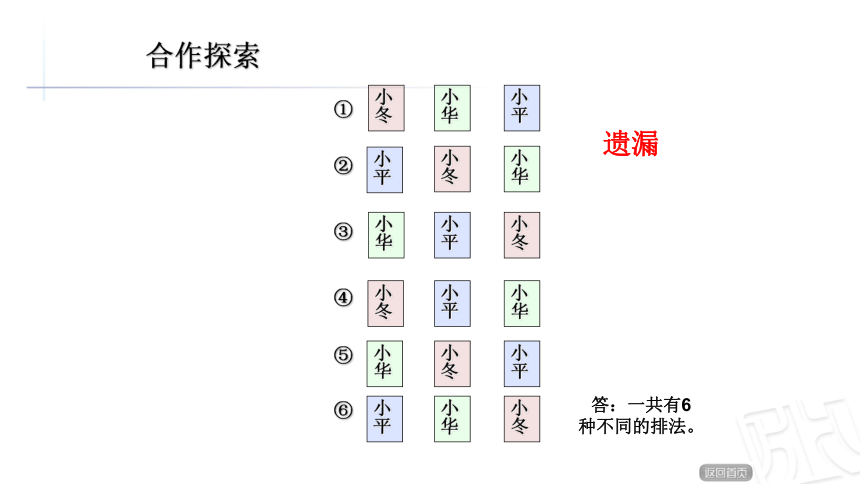
合作探索
遗漏
答:有5种不同的排法。
⑤
小华
小平
小冬
⑥
小平
小华
小冬
答:一共有6种不同的排法。
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小冬
小平
小华
①
②
③
④
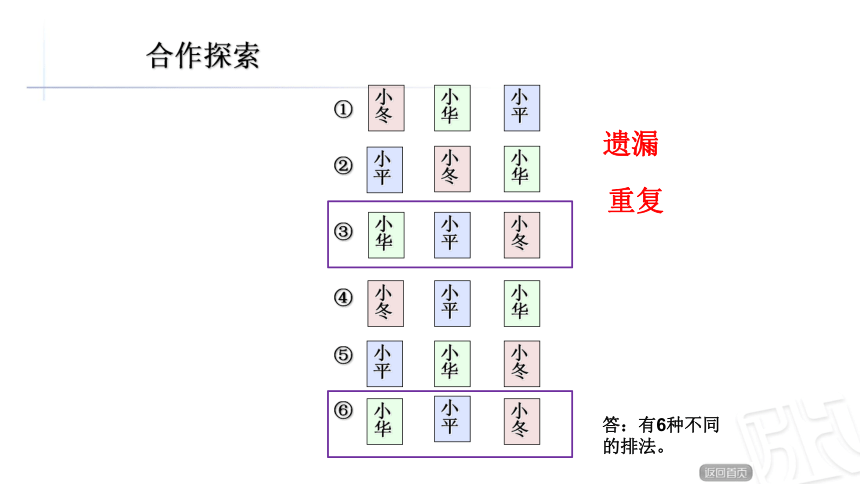
合作探索
⑤
小平
小华
小冬
⑥
小华
小平
小冬
遗漏
重复
答:有6种不同的排法。
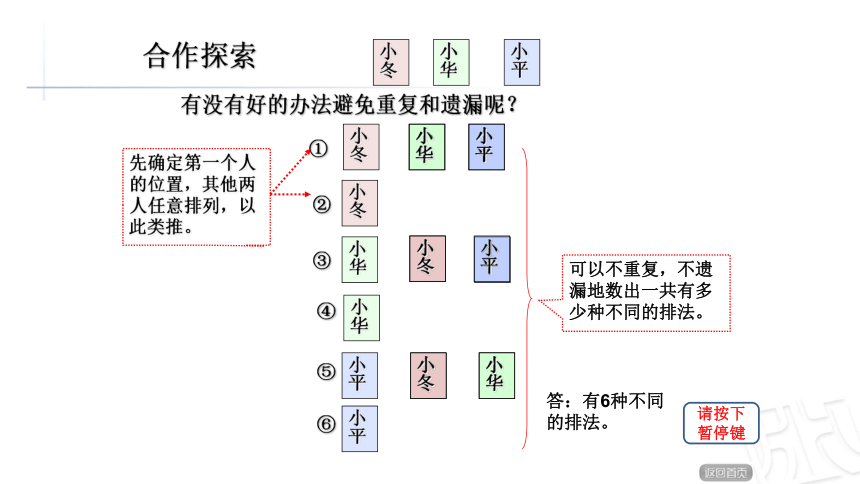
有没有好的办法避免重复和遗漏呢?
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小平
小华
小冬
小华
小平
小冬
小平
小冬
小华
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
合作探索
请按下暂停键
答:有6种不同的排法。
小冬
小华
小平
冬
华
平
冬
华
平
华
平
冬
平
华
冬
华
平
冬
平
冬
华
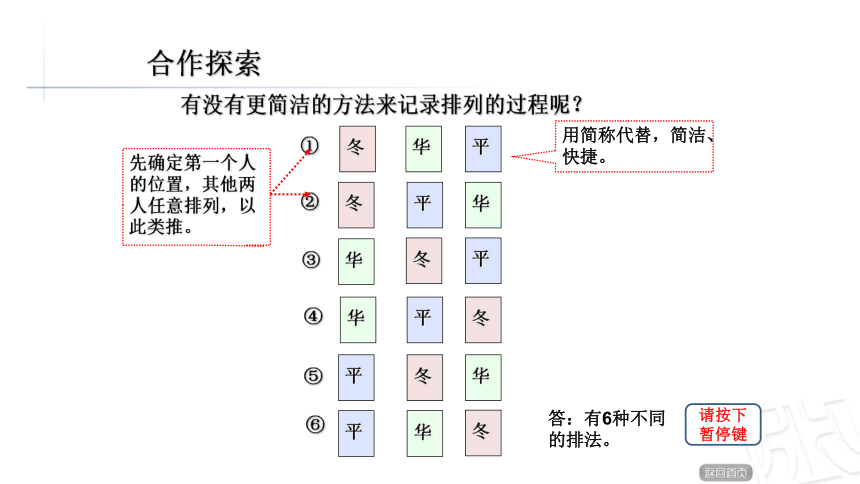
用简称代替,简洁、快捷。
①
②
③
④
⑤
⑥
合作探索
有没有更简洁的方法来记录排列的过程呢?
请按下暂停键
答:有6种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
小冬
小华
小平
①
②
③
④
⑤
⑥
用不同的图形代替不同的人,既直观,又简洁。
合作探索
答:有6种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
A
B
C
A
B
C
B
C
A
C
B
A
B
C
A
C
A
B
①
②
③
④
⑤
⑥
用不同的字母代替不同的人,既简洁,又可以表示任意3种物体的直线排列方法。
小冬
A
小华
B
小平
C
合作探索
答:有6种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
合作探索
其他两人自由排列,数出有
几种排列方法,依次类推,这样可以不重复、不遗漏地数
出一共有多少种排法。
说一说怎样做到不遗漏、不重复呢?
请按下暂停键
先确定第一个人的位置,
合作探索
你能用一道数学算式把以上的排法表示出来吗?
请按下暂停键
3
×
2
=6(种)
表示第一位有3种可能
表示除去第一位后第二位还有2种可能
×
1
表示第三位只剩下1种可能
用下面的数字卡片,你能摆出多少种不同的三位数?分别是多少?
答:有6种不同的排法。
试一试
3
2
4
2
3
4
2
4
3
3
2
4
3
4
2
4
2
3
4
3
2
①
②
③
④
⑤
⑥
请按下暂停键
3
×
2
=6(种)
×
1
用下面的数字卡片,你能摆出多少种不同的三位数?分别是多少?
答:有4种不同的排法。
试一试
3
2
4
0
3
4
0
4
3
3
0
4
3
4
0
4
0
3
4
3
0
0
0不能在
最高位
请按下暂停键
2
×
2
=4(种)
×
1
合作探索
如果4人排列照相呢,一共有多少种不同的排法?
请按下暂停键
B
C
A
D
A
B
C
D
B
B
C
C
C
D
D
B
B
C
D
D
4
×
3
=24(种)
×
2
×
1
自主练习
1.要在酒店大门的上方挂6只大灯笼(如图),如果把形状相同的灯笼挨在一起,可以有多少种不同的挂法?(课本125页自主练习第3题)
答:可以有6种不同的挂法。
A
B
C
AABBCC
AACCBB
BBAACC
BBCCAA
CCAABB
CCBBAA
3
×
2
=6(种)
×
1
请按下暂停键
甲
丁
丙
乙
甲
乙
丙
丁
丙
乙
甲
丁
甲
乙
丁
丙
丙
乙
丁
甲
丁
乙
甲
丙
丁
乙
丙
甲
2.四位同学排一行表演小合唱,丁刚同学担任领唱。固定在左起第二个位置上,其余同学任意排。有多少种不同的排法?(课本125页自主练习第4题)
自主练习
答:有6种不同的排法。
3
×
2
=6(种)
×
1
请按下暂停键
自主练习
0
3.用0—3四个数字可以组成多少个不同的四位数?(每个数字只用一次)(课本125页自主练习第6题)
1023 1032 1203 1230 1302 1320
2013 2031 2103 2130 2301 2310
3012 3021 3102 3120 3201 3210
6个
6个
6个
1
2
3
答:可以组成18个不同的四位数。
请按下暂停键
3
×
3
=18(个)
×
2
×
1
密码的设置
寻找生活中的排列问题
自主练习
彩票中的排列
电话号码的排列
银行卡号的设置
请按下暂停键
排列问题
按一定的顺序进行有序地思考,可以做到不重复、不遗漏。
有序排列的方法:
先确定第一个位置,再确定第二个、第三个位置……看分别有几种可能的情况,就得到了一共有多少种排列的方法,用乘法计算。
列举时用图形或字母来表示会更简洁。
3人排队照相:3×2×1=6(种)
4人排队照相:4×3×2×1=24(种)
智慧广场——排列问题
学习准备:
1.准备好笔和练习本。
3.学习过程中,根据老师的提示,及时按下暂停键,进行问题思考、动手操作和练习等活动。
请按下暂停键
2.准备好写有小冬、小华、小平的学具卡片若干张。
小冬
小华
小平
学习目标
1.在解决问题的过程中,初步发现简单排列现象中的规律,能运用规律解决一些简单的实际问题。
2.在学习中能感知解决问题策略的多样性。
3.感受数学在现实生活中的广泛应用,感受数学的价值。
情境导入
从图中,你知道了哪些数学信息?
小冬、小华、小平3个同学排成一行照相。
有多少种不同的排法?
小冬
小华
小平
合作探索
有多少种不同的排法?
小冬
想一想,排一排(可借助学具卡片),并把研究的结果记录在练习本上。
小华
小平
请按下暂停键
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小冬
小平
小华
①
②
③
④
合作探索
遗漏
答:有5种不同的排法。
⑤
小华
小平
小冬
⑥
小平
小华
小冬
答:一共有6种不同的排法。
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小冬
小平
小华
①
②
③
④
合作探索
⑤
小平
小华
小冬
⑥
小华
小平
小冬
遗漏
重复
答:有6种不同的排法。
有没有好的办法避免重复和遗漏呢?
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小平
小华
小冬
小华
小平
小冬
小平
小冬
小华
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
合作探索
请按下暂停键
答:有6种不同的排法。
小冬
小华
小平
冬
华
平
冬
华
平
华
平
冬
平
华
冬
华
平
冬
平
冬
华
用简称代替,简洁、快捷。
①
②
③
④
⑤
⑥
合作探索
有没有更简洁的方法来记录排列的过程呢?
请按下暂停键
答:有6种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
小冬
小华
小平
①
②
③
④
⑤
⑥
用不同的图形代替不同的人,既直观,又简洁。
合作探索
答:有6种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
A
B
C
A
B
C
B
C
A
C
B
A
B
C
A
C
A
B
①
②
③
④
⑤
⑥
用不同的字母代替不同的人,既简洁,又可以表示任意3种物体的直线排列方法。
小冬
A
小华
B
小平
C
合作探索
答:有6种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
合作探索
其他两人自由排列,数出有
几种排列方法,依次类推,这样可以不重复、不遗漏地数
出一共有多少种排法。
说一说怎样做到不遗漏、不重复呢?
请按下暂停键
先确定第一个人的位置,
合作探索
你能用一道数学算式把以上的排法表示出来吗?
请按下暂停键
3
×
2
=6(种)
表示第一位有3种可能
表示除去第一位后第二位还有2种可能
×
1
表示第三位只剩下1种可能
用下面的数字卡片,你能摆出多少种不同的三位数?分别是多少?
答:有6种不同的排法。
试一试
3
2
4
2
3
4
2
4
3
3
2
4
3
4
2
4
2
3
4
3
2
①
②
③
④
⑤
⑥
请按下暂停键
3
×
2
=6(种)
×
1
用下面的数字卡片,你能摆出多少种不同的三位数?分别是多少?
答:有4种不同的排法。
试一试
3
2
4
0
3
4
0
4
3
3
0
4
3
4
0
4
0
3
4
3
0
0
0不能在
最高位
请按下暂停键
2
×
2
=4(种)
×
1
合作探索
如果4人排列照相呢,一共有多少种不同的排法?
请按下暂停键
B
C
A
D
A
B
C
D
B
B
C
C
C
D
D
B
B
C
D
D
4
×
3
=24(种)
×
2
×
1
自主练习
1.要在酒店大门的上方挂6只大灯笼(如图),如果把形状相同的灯笼挨在一起,可以有多少种不同的挂法?(课本125页自主练习第3题)
答:可以有6种不同的挂法。
A
B
C
AABBCC
AACCBB
BBAACC
BBCCAA
CCAABB
CCBBAA
3
×
2
=6(种)
×
1
请按下暂停键
甲
丁
丙
乙
甲
乙
丙
丁
丙
乙
甲
丁
甲
乙
丁
丙
丙
乙
丁
甲
丁
乙
甲
丙
丁
乙
丙
甲
2.四位同学排一行表演小合唱,丁刚同学担任领唱。固定在左起第二个位置上,其余同学任意排。有多少种不同的排法?(课本125页自主练习第4题)
自主练习
答:有6种不同的排法。
3
×
2
=6(种)
×
1
请按下暂停键
自主练习
0
3.用0—3四个数字可以组成多少个不同的四位数?(每个数字只用一次)(课本125页自主练习第6题)
1023 1032 1203 1230 1302 1320
2013 2031 2103 2130 2301 2310
3012 3021 3102 3120 3201 3210
6个
6个
6个
1
2
3
答:可以组成18个不同的四位数。
请按下暂停键
3
×
3
=18(个)
×
2
×
1
密码的设置
寻找生活中的排列问题
自主练习
彩票中的排列
电话号码的排列
银行卡号的设置
请按下暂停键
排列问题
按一定的顺序进行有序地思考,可以做到不重复、不遗漏。
有序排列的方法:
先确定第一个位置,再确定第二个、第三个位置……看分别有几种可能的情况,就得到了一共有多少种排列的方法,用乘法计算。
列举时用图形或字母来表示会更简洁。
3人排队照相:3×2×1=6(种)
4人排队照相:4×3×2×1=24(种)
