四年级下册数学课件 第5课时组合图形的面积整理与复习 青岛版(五四学制)18张
文档属性
| 名称 | 四年级下册数学课件 第5课时组合图形的面积整理与复习 青岛版(五四学制)18张 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 13:53:16 | ||
图片预览




文档简介
(共18张PPT)
小学数学
四年级下册
多边形的面积整理与复习
学前准备:
1、课本、练习本、剪刀
2、一个平行四边形、两个完全相同的三角形、两个完全相同的梯形纸片
请按暂停键,准备好相关材料
学习目标:
1、通过整理与复习,进一步理解和掌握平行四边形、三角形、梯形面积的计算公式,能灵活运用公式计算图形的面积,解决实际问题。
2、经历回顾、梳理、类比、归纳等过程,沟通图形间的内在联系,构建知识网络,体会转化方法,培养空间观念。
3、感受数学与生活的联系,体验数学的应用价值,享受思维的乐趣。
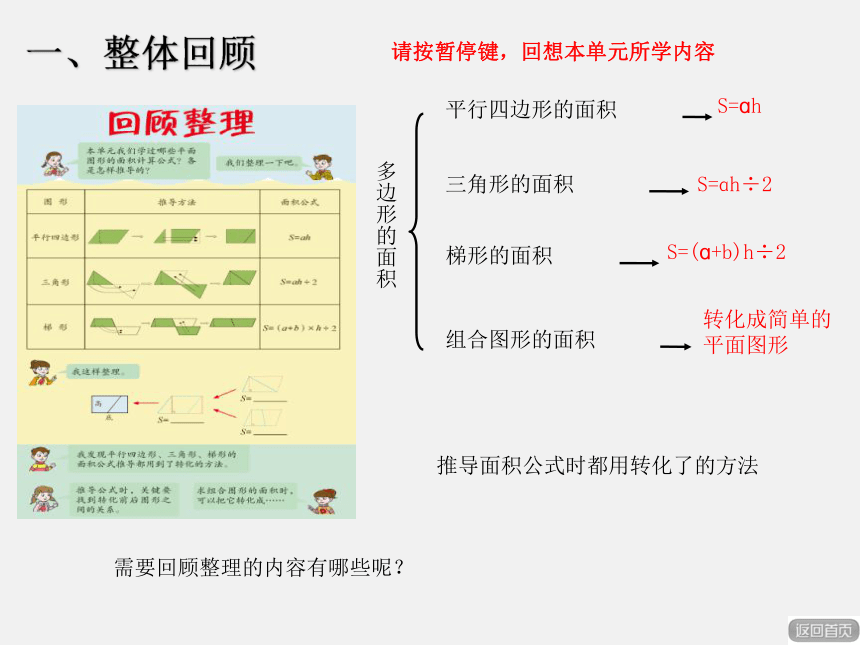
平行四边形的面积
三角形的面积
组合图形的面积
S=ɑh
S=ɑh÷2
梯形的面积
S=(ɑ+b)h÷2
转化成简单的平面图形
多边形的面积
一、整体回顾
需要回顾整理的内容有哪些呢?
推导面积公式时都用转化了的方法
请按暂停键,回想本单元所学内容
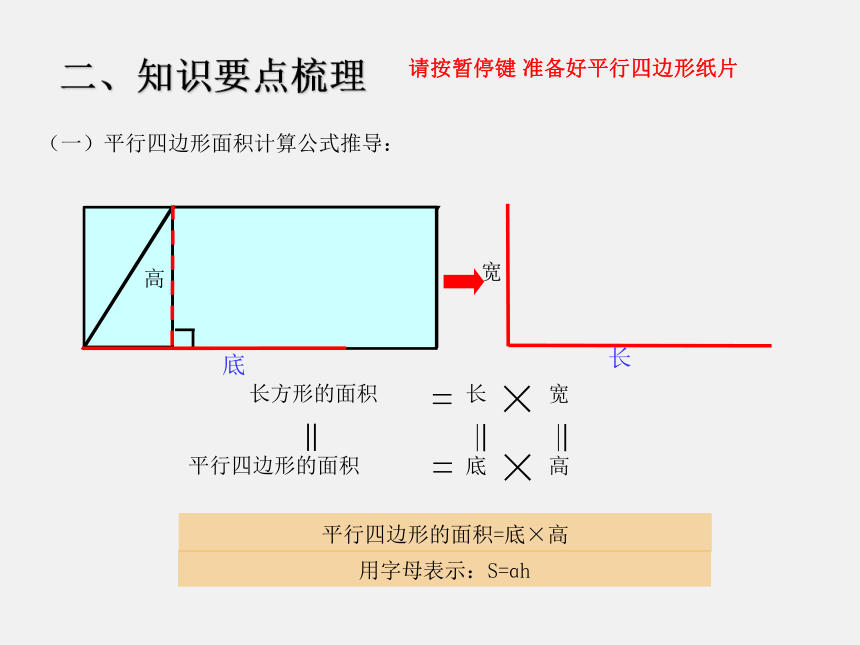
二、知识要点梳理
平行四边形的面积=底×高
长方形的面积
平行四边形的面积
底
长
高
宽
长
底
宽
高
=
×
用字母表示:S=ɑh
=
×
(一)平行四边形面积计算公式推导:
请按暂停键
准备好平行四边形纸片
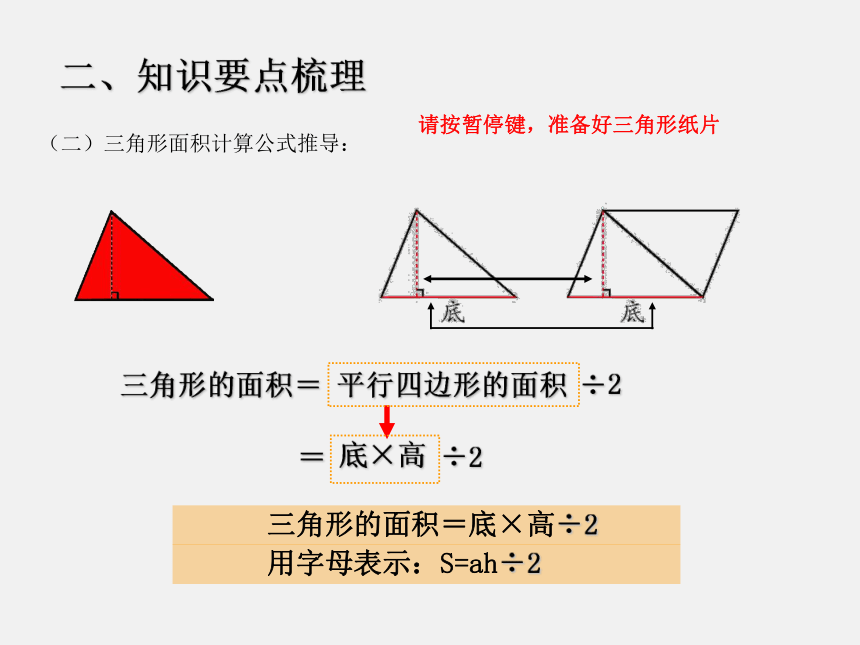
二、知识要点梳理
三角形的面积=
用字母表示:S=ah÷2
÷2
平行四边形的面积
÷2
底×高
=
(二)三角形面积计算公式推导:
三角形的面积=底×高÷2
请按暂停键,准备好三角形纸片
二、知识要点梳理
梯形的面积
÷
2
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
=
梯形的面积
=
×
高
÷
2
用字母表示:
S
(上底+下底)
=
(a+b)
h
÷
2
下底
上底
高
下底
上底
(三)梯形面积计算公式推导:
请按暂停键,准备好梯形纸片
10cm
8cm
12cm
4cm
分割法:画辅助线将组合图形分割转化为两个或两个以上的基本图形的方法。
添补法:通过添加辅助线,将组合图形转化成基本图形的方法。
(四)组合图形的面积
二、知识要点梳理
S组合=
S三角形
+
S长方形
(10-4)×(12-8)÷2
+10×8
=
92(cm2)
S组合=
S大长方形
–
S梯形
10×12-(10+4)×(12-8)÷2
=
92(cm2)
10cm
8cm
12cm
4
请按暂停键,想一想组合图形的面积是如何计算的?
a
a
a
b
a
b
h
h
a
h
S=ah
S=ah÷2
S=(a+b)h÷2
转化
转化
转化
a
b
S=ab
二、知识要点梳理
(五)图形之间的联系:
二、知识要点梳理
(六)转化
转化:是一种重要的数学思想方法,所谓转化,就是把所要解决的问题转化为另一个较容易解决的问题或已经解决的问题,具体地说,就是说把“新知”转化为“旧知”,把“未知”转化为“已知”,把“复杂”转化为“简单”。
三、综合应用
1、课本第38页——我学会了吗
绿色小麦小麦区
每平方米每年产优质小麦0.75千克
蔬菜区(一)
每平方米每年辣椒产值约25元
(1)绿色小麦区的面积是多少平方米?每年可以产多少千克优质小麦?
(2)蔬菜区辣椒的产值每年约为多少元?
请按暂停键,完成解答
(1)绿色小麦区的面积是多少平方米?每年可以产多少千克优质小麦?
360×300=108000(平方米)
108000×0.75=81000(千克)
答:绿色小麦区的面积是108000平方米,每年可以产81000千克优质小麦。
(2)蔬菜区辣椒的产值每年约为多少元?
(360+240)×300÷2
=600×300÷2
=180000÷2
=90000(平方米)
90000×25=2250000(元)
答:蔬菜区辣椒的产值每年约为2250000元。
三、综合应用
20米
20米
2、求下图中阴影部分的面积。
10米
10米
(20-10)×20÷2=100(平方米)
10
×10÷2=50(平方米)
100+50=150(平方米)
把阴影部分分割成两个三角形。
答:阴影部分的面积是150(平方米)
请按暂停键,完成解答
三、综合应用
3、思维挑战
工厂有一堆木材(如右图)。
求一共有多少根木材?
可以用下面的方法求总根数:
(顶层根数+底层根数)×层数÷2
思考:为什么这样计算呢?你知道吗?
请按暂停键,仔细观察后想一想
(2+6)×5÷2
=8×5÷2
=20(根)
四、课堂小结
按暂停键,用自己喜欢的方式把这节课复习的内容整理一下
四、课堂小结
圆的面积——化圆为方(转化)
小学数学
四年级下册
多边形的面积整理与复习
学前准备:
1、课本、练习本、剪刀
2、一个平行四边形、两个完全相同的三角形、两个完全相同的梯形纸片
请按暂停键,准备好相关材料
学习目标:
1、通过整理与复习,进一步理解和掌握平行四边形、三角形、梯形面积的计算公式,能灵活运用公式计算图形的面积,解决实际问题。
2、经历回顾、梳理、类比、归纳等过程,沟通图形间的内在联系,构建知识网络,体会转化方法,培养空间观念。
3、感受数学与生活的联系,体验数学的应用价值,享受思维的乐趣。
平行四边形的面积
三角形的面积
组合图形的面积
S=ɑh
S=ɑh÷2
梯形的面积
S=(ɑ+b)h÷2
转化成简单的平面图形
多边形的面积
一、整体回顾
需要回顾整理的内容有哪些呢?
推导面积公式时都用转化了的方法
请按暂停键,回想本单元所学内容
二、知识要点梳理
平行四边形的面积=底×高
长方形的面积
平行四边形的面积
底
长
高
宽
长
底
宽
高
=
×
用字母表示:S=ɑh
=
×
(一)平行四边形面积计算公式推导:
请按暂停键
准备好平行四边形纸片
二、知识要点梳理
三角形的面积=
用字母表示:S=ah÷2
÷2
平行四边形的面积
÷2
底×高
=
(二)三角形面积计算公式推导:
三角形的面积=底×高÷2
请按暂停键,准备好三角形纸片
二、知识要点梳理
梯形的面积
÷
2
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
=
梯形的面积
=
×
高
÷
2
用字母表示:
S
(上底+下底)
=
(a+b)
h
÷
2
下底
上底
高
下底
上底
(三)梯形面积计算公式推导:
请按暂停键,准备好梯形纸片
10cm
8cm
12cm
4cm
分割法:画辅助线将组合图形分割转化为两个或两个以上的基本图形的方法。
添补法:通过添加辅助线,将组合图形转化成基本图形的方法。
(四)组合图形的面积
二、知识要点梳理
S组合=
S三角形
+
S长方形
(10-4)×(12-8)÷2
+10×8
=
92(cm2)
S组合=
S大长方形
–
S梯形
10×12-(10+4)×(12-8)÷2
=
92(cm2)
10cm
8cm
12cm
4
请按暂停键,想一想组合图形的面积是如何计算的?
a
a
a
b
a
b
h
h
a
h
S=ah
S=ah÷2
S=(a+b)h÷2
转化
转化
转化
a
b
S=ab
二、知识要点梳理
(五)图形之间的联系:
二、知识要点梳理
(六)转化
转化:是一种重要的数学思想方法,所谓转化,就是把所要解决的问题转化为另一个较容易解决的问题或已经解决的问题,具体地说,就是说把“新知”转化为“旧知”,把“未知”转化为“已知”,把“复杂”转化为“简单”。
三、综合应用
1、课本第38页——我学会了吗
绿色小麦小麦区
每平方米每年产优质小麦0.75千克
蔬菜区(一)
每平方米每年辣椒产值约25元
(1)绿色小麦区的面积是多少平方米?每年可以产多少千克优质小麦?
(2)蔬菜区辣椒的产值每年约为多少元?
请按暂停键,完成解答
(1)绿色小麦区的面积是多少平方米?每年可以产多少千克优质小麦?
360×300=108000(平方米)
108000×0.75=81000(千克)
答:绿色小麦区的面积是108000平方米,每年可以产81000千克优质小麦。
(2)蔬菜区辣椒的产值每年约为多少元?
(360+240)×300÷2
=600×300÷2
=180000÷2
=90000(平方米)
90000×25=2250000(元)
答:蔬菜区辣椒的产值每年约为2250000元。
三、综合应用
20米
20米
2、求下图中阴影部分的面积。
10米
10米
(20-10)×20÷2=100(平方米)
10
×10÷2=50(平方米)
100+50=150(平方米)
把阴影部分分割成两个三角形。
答:阴影部分的面积是150(平方米)
请按暂停键,完成解答
三、综合应用
3、思维挑战
工厂有一堆木材(如右图)。
求一共有多少根木材?
可以用下面的方法求总根数:
(顶层根数+底层根数)×层数÷2
思考:为什么这样计算呢?你知道吗?
请按暂停键,仔细观察后想一想
(2+6)×5÷2
=8×5÷2
=20(根)
四、课堂小结
按暂停键,用自己喜欢的方式把这节课复习的内容整理一下
四、课堂小结
圆的面积——化圆为方(转化)
