2020-2021学年人教五四新版六年级下册数学期末冲刺试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年人教五四新版六年级下册数学期末冲刺试题(Word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 00:00:00 | ||
图片预览




文档简介
2020-2021学年人教五四新版六年级下册数学期末冲刺试题
一.选择题(共10小题,满分30分,每小题3分)
1.的相反数是( )
A.3
B.
C.﹣3
D.
2.在下列数π,+1,6.7,﹣15,0,,﹣1,25%中,属于整数的有( )
A.2个
B.3个
C.4个
D.5个
3.计算:|﹣6|+1的结果是( )
A.﹣5
B.2
C.7
D.9
4.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
5.能清楚的看出每个项目的具体数量的统计图是( )
A.扇形统计图
B.折线统计图
C.条形统计图
D.以上三种均可
6.下列说法正确的是( )
A.多项式x2+2x2y+1是二次三项式
B.单项式2x2y的次数是2
C.0是单项式
D.单项式﹣3πx2y的系数是﹣3
7.下列变形正确的是( )
A.x﹣y+z=x﹣(y﹣z)
B.x﹣y﹣z=x+(y﹣z)
C.x+y﹣z=x+(y+z)
D.x+y+z=x﹣(﹣y+z)
8.下列说法:①经过三点中的两点画直线一定可以画三条直线:
②两点之间,线段最短;
③若点M是AB的中点,则MA=MB;
④同角的余角相等
其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
9.下列说法中正确的是( )
A.最小的整数是0
B.有理数分为正数和负数
C.如果两个数的绝对值相等,那么这两个数相等
D.互为相反数的两个数的绝对值相等
10.如图,点O在直线AE上,OC平分∠AOE,∠BOD是直角.若∠1=25°,那么∠BOE的度数是( )
A.90°
B.145°
C.155°
D.165°
二.填空题(共10小题,满分30分,每小题3分)
11.人的血管首尾相连的长度大约可达96000千米,96000千米用科学记数法表示为
米.
12.已知单项式﹣x2y3的系数是m,次数是n,则mn=
.
13.﹣的倒数是
.
14.已知7xay2和﹣9x5yb是同类项,则=
.
15.观察下面的一列单项式:﹣2x、4x3、﹣8x5、16x7、…根据你发现的规律,第n个单项式为
.
16.如图,数轴上的点A所表示的数为a,化简|a|﹣|a﹣2|的结果为
.
17.现将某校七年一班女生按照身高共分成三组,下表是这个班级女生的身高分组情况统计表,则在统计表中b的值是
.
第一组
第二组
第三组
每个小组女生的人数
9
8
a
每个小组女生人数占班级女生人数的百分比
b
c
15%
18.如图,已知线段AB=8cm,M是AB的中点,P是线段MB上一点,N为PB的中点,NB=1.5cm,则线段MP=
cm.
19.我市某天上午的气温为﹣2℃,中午上升了6℃,下午受冷空气的影响,到夜间温度下降了9℃,则这天夜间的气温为
.
20.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN.若∠NEC=36°,则∠FMN=
°.
三.解答题(共7小题,满分60分)
21.(6分)某同学做一道数学题:两个多项式A、B,B=2x2﹣4x﹣6,试求A﹣2B.这位同学把“A﹣2B”看成“A+2B”,结果求出的答案是7x2﹣8x﹣11,那么,A﹣2B的正确答案是多少?
22.(6分)一个几何体由大小相同的立方块搭成,从上面看到的形状如图所示,其中小正方形中的数字表示在该位置的立方块个数.
①在所给的方框中分别画出该几何体从正面,从左面看到的形状图;
②若允许从该几何体中拿掉部分立方块,使剩下的几何体从正面看到的形状图和原几何体从上面看到的形状图相同,则最多可拿掉
个立方块.
23.(12分)计算:()×12
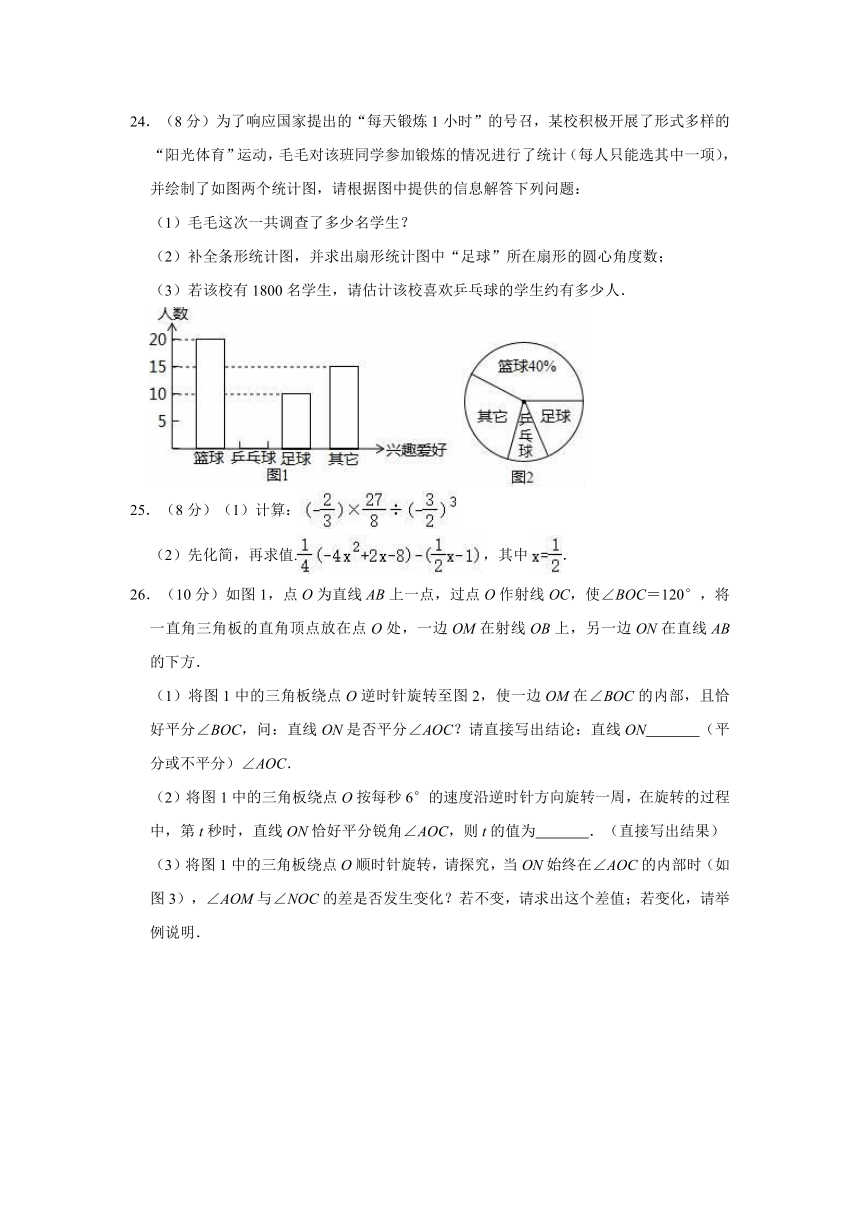
24.(8分)为了响应国家提出的“每天锻炼1小时”的号召,某校积极开展了形式多样的“阳光体育”运动,毛毛对该班同学参加锻炼的情况进行了统计(每人只能选其中一项),并绘制了如图两个统计图,请根据图中提供的信息解答下列问题:
(1)毛毛这次一共调查了多少名学生?
(2)补全条形统计图,并求出扇形统计图中“足球”所在扇形的圆心角度数;
(3)若该校有1800名学生,请估计该校喜欢乒乓球的学生约有多少人.
25.(8分)(1)计算:
(2)先化简,再求值.,其中.
26.(10分)如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请直接写出结论:直线ON
(平分或不平分)∠AOC.
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为
.(直接写出结果)
(3)将图1中的三角板绕点O顺时针旋转,请探究,当ON始终在∠AOC的内部时(如图3),∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
27.(10分)已知数轴上两点A,B对应的数分别为a,b,点M为数轴上一动点,其中a,b满足(a+2)2+|b﹣7|=0.
(1)写出点A表示的数是
;点B表示的数是
.
(2)若点M到A的距离是点M到B的距离的两倍,我们就称点M是[A,B]的好点.
①若点M到运动到原点O时,此时点M
[A,B]的好点(填是或者不是)
②若点M以每秒1个单位的速度从原点O开始运动,当M是[A,B]的好点时,求点M所表示的数.
(3)试探究线段BM和AM的差即BM﹣AM的值是否一定发生变化?若变化,请说明理由:若不变,请求其值.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:依据只有符号不同的两个数互为相反数得:的相反数是.
故选:D.
2.解:在数π,+1,6.7,﹣15,0,,﹣1,25%中,属于整数的有+1,﹣15,0,﹣1,一共4个.
故选:C.
3.解:原式=6+1=7,
故选:C.
4.解:A、B、D中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.C围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故C不能围成三棱柱.
故选:C.
5.解:条形统计图能清楚地表示出每个项目的具体数目,故C符合题意.
故选:C.
6.解:A.多项式x2+2x2y+1是三次三项式,此选项错误;
B.单项式2x2y的次数是3,此选项错误;
C.0是单项式,此选项正确;
D.单项式﹣3πx2y的系数是﹣3π,此选项错误;
故选:C.
7.解:(B)原式=x﹣(y+z),故B错误;
(C)原式=x+(y﹣z),故C错误;
(D)原式=x+(y+z),故D错误;
故选:A.
8.解:A.过同一平面上的不共线的三点中的任意两点画直线,可以画三条直线,故选项A错误;
B.两点之间,线段最短,故选项正确;
C.若点M是AB的中点,则MA=MB,故选项正确;
D.同角的余角相等,故选项正确;
所以正确的说法有②③④共3个.
故选:B.
9.解:A、因为整数包括正整数和负整数,0大于负数,所以最小的整数是0错误;
B、因为0既不是正数也不是负数,但是有理数,所以有理数分为正数和负数错误;
C、因为:如+1和﹣1的绝对值相等,但+1不等于﹣1,所以如果两个数的绝对值相等,那么这两个数相等错误;
D、由相反数的意义和数轴,互为相反数的两个数的绝对值相等,如|+1|=|﹣1|=1,所以正确;
故选:D.
10.解:∵点O在直线AE上,OC平分∠AOE,
∴∠AOC=∠COE=90°,
∵∠DOB是直角,∠1=25°,
∴∠BOC=∠DOB﹣∠1=90°﹣25°=65°,
∴∠BOE=∠COE+∠BOC=90°+65°=155°.
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:96000千米=96000000=9.6×107(米).
故答案为:9.6×107.
12.解:∵单项式﹣x2y3的系数为m=﹣,次数为n=5,
∴mn的值为:﹣×5=﹣2.
故答案为:﹣2.
13.解:﹣的倒数是﹣8,
故答案为:﹣8.
14.解:由题意可知:a=5,b=2,
∴原式=.
故答案为:.
15.解:∵﹣2x=(﹣1)1?21?x1;
4x3=(﹣1)2?22?x3;
8x5=(﹣1)3?23?x5;
﹣16x7=(﹣1)4?24?x7.
第n个单项式为(﹣1)n?2n?x2n﹣1.
故答案为:(﹣1)n2nx2n﹣1.
16.解:由数轴知:1<a<2,
∴a﹣2<0,
∴|a|﹣|a﹣2|=a+(a﹣2)=a+a﹣2=2a﹣2.
故答案为:2a﹣2.
17.解:由表知被调查的总人数为(9+8)÷(1﹣15%)=20,
∴b=9÷20×100%=45%,
故答案为:45%.
18.解:∵M是AB的中点,AB=8cm,
∴AM=BM=4cm,
∵N为PB的中点,NB=1.5cm,
∴PB=2NB=3cm,
∴MP=BM﹣PB=4﹣3=1cm.
故答案为1.
19.解:﹣2+6﹣9
=4﹣9
=﹣5(℃)
答:这天夜间的气温为﹣5℃.
故答案为:﹣5℃.
20.解:∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∵将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,
∴∠F=∠A=90°,∠FEN=∠C=90°,∠DNM=∠ENM,
∵∠NEC=36°,
∴∠ENC=54°,
∴∠ENM=(180°﹣∠ENC)=(180°﹣54°)=63°,
∴∠FMN=360°﹣90°﹣90°﹣63°=117°,
故答案为:117.
三.解答题(共7小题,满分60分)
21.解:∵A+2B=7x2﹣8x﹣11,
∴A=7x2﹣8x﹣11﹣2B
=7x2﹣8x﹣11﹣2(2x2﹣4x﹣6)
=7x2﹣8x﹣11﹣4x2+8x+12
=3x2+1
∴A﹣2B=3x2+1﹣2(2x2﹣4x﹣6)
=3x2+1﹣4x2+8x+12
=﹣x2+8x+13.
答:A﹣2B的正确答案是﹣x2+8x+13.
22.解:①该几何体从正面,从左面看到的图形如图所示:
②拿掉后,剩下的几何体从正面看到的形状图和原几何体从上面看到的形状图相同,则最多可拿掉5个,
故答案为:5.
23.解:原式=(10﹣9)÷(﹣4)+1=﹣+1=.
24.解:(1)20÷40%=50(名),
答:毛毛一共调查了50名学生;
(2)50﹣20﹣10﹣15=5(名),360°×=72°,
答:扇形统计图中“足球”所在扇形的圆心角为72°,补全条形统计图如图所示:
(3)1800×=180(名),
答:该校1800名学生中喜欢乒乓球的约有180名.
25.解:(1)原式=××=;
(2)原式=﹣x2+x﹣2﹣x+1=﹣x2﹣1,
当x=时,原式=﹣1.
26.解:(1)直线ON平分∠AOC.
理由如下:
设ON的反向延长线为OD,
∵OM平分∠BOC,∠BOC=120°,
∴∠MOC=∠MOB=∠BOC=60°,
又∠MOD=∠MON=90°,
∴∠COD=90°﹣∠MOC=30°,
∵∠AOC=180°﹣∠BOC=60°,
∴∠COD=∠AOC,
∴OD平分∠AOC,
即直线ON平分∠AOC,
故答案为:平分;
(2)∵∠BOC=120°,
∴∠AOC=60°.
∴∠BON=∠COD=30°.
即旋转60°或240°时直线ON平分∠AOC.
由题意得,6t=60或240.
解得:t=10或40,
故答案为:10或40;
(3)∠AOM﹣∠NOC的差不变.
∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON.
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.
∴∠AOM与∠NOC的差不变,这个差值是30°.
27.解:(1)∵(a+2)2+|b﹣7|=0,
∴a+2=0,b﹣7=0,
∴a=﹣2,b=7;
(2)①AM=2,BM=7,
2×2=4≠7,
故点M不是【A,B】的好点;
②当点M在点B的右侧时,
t+2=2(t﹣7),
解得t=16;
当点M在点A与B之间时,
t+2=2(7﹣t),
解得t=4;
当点M在点A的左侧时,
﹣2+t=2(7+t),
解得t=﹣16(不合题意舍去).
故点M的运动方向是向右,运动时间是4或16秒;
(3)线段BM与AM的差即BM﹣AM的值发生变化,理由是:
设点M对应的数为c,
由BM=|c﹣7|,AM=|c+2|,
则分三种情况:当点M在点B的右侧时,
BM﹣AM=c﹣7﹣c22=﹣9;
当点M在点A与B之间时,BM﹣AM=7﹣c﹣c﹣2=5﹣2c,
当点M在点A的左侧时,BM﹣AM=7﹣c+c+2=9.
故答案为:﹣2,7,不是.
一.选择题(共10小题,满分30分,每小题3分)
1.的相反数是( )
A.3
B.
C.﹣3
D.
2.在下列数π,+1,6.7,﹣15,0,,﹣1,25%中,属于整数的有( )
A.2个
B.3个
C.4个
D.5个
3.计算:|﹣6|+1的结果是( )
A.﹣5
B.2
C.7
D.9
4.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
5.能清楚的看出每个项目的具体数量的统计图是( )
A.扇形统计图
B.折线统计图
C.条形统计图
D.以上三种均可
6.下列说法正确的是( )
A.多项式x2+2x2y+1是二次三项式
B.单项式2x2y的次数是2
C.0是单项式
D.单项式﹣3πx2y的系数是﹣3
7.下列变形正确的是( )
A.x﹣y+z=x﹣(y﹣z)
B.x﹣y﹣z=x+(y﹣z)
C.x+y﹣z=x+(y+z)
D.x+y+z=x﹣(﹣y+z)
8.下列说法:①经过三点中的两点画直线一定可以画三条直线:
②两点之间,线段最短;
③若点M是AB的中点,则MA=MB;
④同角的余角相等
其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
9.下列说法中正确的是( )
A.最小的整数是0
B.有理数分为正数和负数
C.如果两个数的绝对值相等,那么这两个数相等
D.互为相反数的两个数的绝对值相等
10.如图,点O在直线AE上,OC平分∠AOE,∠BOD是直角.若∠1=25°,那么∠BOE的度数是( )
A.90°
B.145°
C.155°
D.165°
二.填空题(共10小题,满分30分,每小题3分)
11.人的血管首尾相连的长度大约可达96000千米,96000千米用科学记数法表示为
米.
12.已知单项式﹣x2y3的系数是m,次数是n,则mn=
.
13.﹣的倒数是
.
14.已知7xay2和﹣9x5yb是同类项,则=
.
15.观察下面的一列单项式:﹣2x、4x3、﹣8x5、16x7、…根据你发现的规律,第n个单项式为
.
16.如图,数轴上的点A所表示的数为a,化简|a|﹣|a﹣2|的结果为
.
17.现将某校七年一班女生按照身高共分成三组,下表是这个班级女生的身高分组情况统计表,则在统计表中b的值是
.
第一组
第二组
第三组
每个小组女生的人数
9
8
a
每个小组女生人数占班级女生人数的百分比
b
c
15%
18.如图,已知线段AB=8cm,M是AB的中点,P是线段MB上一点,N为PB的中点,NB=1.5cm,则线段MP=
cm.
19.我市某天上午的气温为﹣2℃,中午上升了6℃,下午受冷空气的影响,到夜间温度下降了9℃,则这天夜间的气温为
.
20.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN.若∠NEC=36°,则∠FMN=
°.
三.解答题(共7小题,满分60分)
21.(6分)某同学做一道数学题:两个多项式A、B,B=2x2﹣4x﹣6,试求A﹣2B.这位同学把“A﹣2B”看成“A+2B”,结果求出的答案是7x2﹣8x﹣11,那么,A﹣2B的正确答案是多少?
22.(6分)一个几何体由大小相同的立方块搭成,从上面看到的形状如图所示,其中小正方形中的数字表示在该位置的立方块个数.
①在所给的方框中分别画出该几何体从正面,从左面看到的形状图;
②若允许从该几何体中拿掉部分立方块,使剩下的几何体从正面看到的形状图和原几何体从上面看到的形状图相同,则最多可拿掉
个立方块.
23.(12分)计算:()×12
24.(8分)为了响应国家提出的“每天锻炼1小时”的号召,某校积极开展了形式多样的“阳光体育”运动,毛毛对该班同学参加锻炼的情况进行了统计(每人只能选其中一项),并绘制了如图两个统计图,请根据图中提供的信息解答下列问题:
(1)毛毛这次一共调查了多少名学生?
(2)补全条形统计图,并求出扇形统计图中“足球”所在扇形的圆心角度数;
(3)若该校有1800名学生,请估计该校喜欢乒乓球的学生约有多少人.
25.(8分)(1)计算:
(2)先化简,再求值.,其中.
26.(10分)如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请直接写出结论:直线ON
(平分或不平分)∠AOC.
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为
.(直接写出结果)
(3)将图1中的三角板绕点O顺时针旋转,请探究,当ON始终在∠AOC的内部时(如图3),∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
27.(10分)已知数轴上两点A,B对应的数分别为a,b,点M为数轴上一动点,其中a,b满足(a+2)2+|b﹣7|=0.
(1)写出点A表示的数是
;点B表示的数是
.
(2)若点M到A的距离是点M到B的距离的两倍,我们就称点M是[A,B]的好点.
①若点M到运动到原点O时,此时点M
[A,B]的好点(填是或者不是)
②若点M以每秒1个单位的速度从原点O开始运动,当M是[A,B]的好点时,求点M所表示的数.
(3)试探究线段BM和AM的差即BM﹣AM的值是否一定发生变化?若变化,请说明理由:若不变,请求其值.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:依据只有符号不同的两个数互为相反数得:的相反数是.
故选:D.
2.解:在数π,+1,6.7,﹣15,0,,﹣1,25%中,属于整数的有+1,﹣15,0,﹣1,一共4个.
故选:C.
3.解:原式=6+1=7,
故选:C.
4.解:A、B、D中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.C围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故C不能围成三棱柱.
故选:C.
5.解:条形统计图能清楚地表示出每个项目的具体数目,故C符合题意.
故选:C.
6.解:A.多项式x2+2x2y+1是三次三项式,此选项错误;
B.单项式2x2y的次数是3,此选项错误;
C.0是单项式,此选项正确;
D.单项式﹣3πx2y的系数是﹣3π,此选项错误;
故选:C.
7.解:(B)原式=x﹣(y+z),故B错误;
(C)原式=x+(y﹣z),故C错误;
(D)原式=x+(y+z),故D错误;
故选:A.
8.解:A.过同一平面上的不共线的三点中的任意两点画直线,可以画三条直线,故选项A错误;
B.两点之间,线段最短,故选项正确;
C.若点M是AB的中点,则MA=MB,故选项正确;
D.同角的余角相等,故选项正确;
所以正确的说法有②③④共3个.
故选:B.
9.解:A、因为整数包括正整数和负整数,0大于负数,所以最小的整数是0错误;
B、因为0既不是正数也不是负数,但是有理数,所以有理数分为正数和负数错误;
C、因为:如+1和﹣1的绝对值相等,但+1不等于﹣1,所以如果两个数的绝对值相等,那么这两个数相等错误;
D、由相反数的意义和数轴,互为相反数的两个数的绝对值相等,如|+1|=|﹣1|=1,所以正确;
故选:D.
10.解:∵点O在直线AE上,OC平分∠AOE,
∴∠AOC=∠COE=90°,
∵∠DOB是直角,∠1=25°,
∴∠BOC=∠DOB﹣∠1=90°﹣25°=65°,
∴∠BOE=∠COE+∠BOC=90°+65°=155°.
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:96000千米=96000000=9.6×107(米).
故答案为:9.6×107.
12.解:∵单项式﹣x2y3的系数为m=﹣,次数为n=5,
∴mn的值为:﹣×5=﹣2.
故答案为:﹣2.
13.解:﹣的倒数是﹣8,
故答案为:﹣8.
14.解:由题意可知:a=5,b=2,
∴原式=.
故答案为:.
15.解:∵﹣2x=(﹣1)1?21?x1;
4x3=(﹣1)2?22?x3;
8x5=(﹣1)3?23?x5;
﹣16x7=(﹣1)4?24?x7.
第n个单项式为(﹣1)n?2n?x2n﹣1.
故答案为:(﹣1)n2nx2n﹣1.
16.解:由数轴知:1<a<2,
∴a﹣2<0,
∴|a|﹣|a﹣2|=a+(a﹣2)=a+a﹣2=2a﹣2.
故答案为:2a﹣2.
17.解:由表知被调查的总人数为(9+8)÷(1﹣15%)=20,
∴b=9÷20×100%=45%,
故答案为:45%.
18.解:∵M是AB的中点,AB=8cm,
∴AM=BM=4cm,
∵N为PB的中点,NB=1.5cm,
∴PB=2NB=3cm,
∴MP=BM﹣PB=4﹣3=1cm.
故答案为1.
19.解:﹣2+6﹣9
=4﹣9
=﹣5(℃)
答:这天夜间的气温为﹣5℃.
故答案为:﹣5℃.
20.解:∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∵将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,
∴∠F=∠A=90°,∠FEN=∠C=90°,∠DNM=∠ENM,
∵∠NEC=36°,
∴∠ENC=54°,
∴∠ENM=(180°﹣∠ENC)=(180°﹣54°)=63°,
∴∠FMN=360°﹣90°﹣90°﹣63°=117°,
故答案为:117.
三.解答题(共7小题,满分60分)
21.解:∵A+2B=7x2﹣8x﹣11,
∴A=7x2﹣8x﹣11﹣2B
=7x2﹣8x﹣11﹣2(2x2﹣4x﹣6)
=7x2﹣8x﹣11﹣4x2+8x+12
=3x2+1
∴A﹣2B=3x2+1﹣2(2x2﹣4x﹣6)
=3x2+1﹣4x2+8x+12
=﹣x2+8x+13.
答:A﹣2B的正确答案是﹣x2+8x+13.
22.解:①该几何体从正面,从左面看到的图形如图所示:
②拿掉后,剩下的几何体从正面看到的形状图和原几何体从上面看到的形状图相同,则最多可拿掉5个,
故答案为:5.
23.解:原式=(10﹣9)÷(﹣4)+1=﹣+1=.
24.解:(1)20÷40%=50(名),
答:毛毛一共调查了50名学生;
(2)50﹣20﹣10﹣15=5(名),360°×=72°,
答:扇形统计图中“足球”所在扇形的圆心角为72°,补全条形统计图如图所示:
(3)1800×=180(名),
答:该校1800名学生中喜欢乒乓球的约有180名.
25.解:(1)原式=××=;
(2)原式=﹣x2+x﹣2﹣x+1=﹣x2﹣1,
当x=时,原式=﹣1.
26.解:(1)直线ON平分∠AOC.
理由如下:
设ON的反向延长线为OD,
∵OM平分∠BOC,∠BOC=120°,
∴∠MOC=∠MOB=∠BOC=60°,
又∠MOD=∠MON=90°,
∴∠COD=90°﹣∠MOC=30°,
∵∠AOC=180°﹣∠BOC=60°,
∴∠COD=∠AOC,
∴OD平分∠AOC,
即直线ON平分∠AOC,
故答案为:平分;
(2)∵∠BOC=120°,
∴∠AOC=60°.
∴∠BON=∠COD=30°.
即旋转60°或240°时直线ON平分∠AOC.
由题意得,6t=60或240.
解得:t=10或40,
故答案为:10或40;
(3)∠AOM﹣∠NOC的差不变.
∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON.
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.
∴∠AOM与∠NOC的差不变,这个差值是30°.
27.解:(1)∵(a+2)2+|b﹣7|=0,
∴a+2=0,b﹣7=0,
∴a=﹣2,b=7;
(2)①AM=2,BM=7,
2×2=4≠7,
故点M不是【A,B】的好点;
②当点M在点B的右侧时,
t+2=2(t﹣7),
解得t=16;
当点M在点A与B之间时,
t+2=2(7﹣t),
解得t=4;
当点M在点A的左侧时,
﹣2+t=2(7+t),
解得t=﹣16(不合题意舍去).
故点M的运动方向是向右,运动时间是4或16秒;
(3)线段BM与AM的差即BM﹣AM的值发生变化,理由是:
设点M对应的数为c,
由BM=|c﹣7|,AM=|c+2|,
则分三种情况:当点M在点B的右侧时,
BM﹣AM=c﹣7﹣c22=﹣9;
当点M在点A与B之间时,BM﹣AM=7﹣c﹣c﹣2=5﹣2c,
当点M在点A的左侧时,BM﹣AM=7﹣c+c+2=9.
故答案为:﹣2,7,不是.
同课章节目录
