七年级下册数学第七章三角形导学案(无答案)
文档属性
| 名称 | 七年级下册数学第七章三角形导学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 126.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-14 00:00:00 | ||
图片预览



文档简介
第七章三角形导学案
课题:7.1.1三角形的边(1)
一、教材分析:
(一)学习目标:
1.知道什么是三角形及其边、顶点、角,会用符号表示三角形.
2.知道什么是锐角三角形、直角三角形、钝角三角形,会按角将三角形分类.
3.知道什么是等腰三角形、等边三角形,会按边将三角形分类.
(二)学习重点和难点:
1.重点:三角形及其有关的概念、三角形的分类.
2.难点:按边将三角形分类.
二、教学过程:
1.任务导读单:阅读P62—64页回答下列问题:
1.三角形是最简单的______图形,也是认识许多其他图形的________.本章将学习与三角形有关的_____和_____,并借助三角形中三个角的和等于____探究________________.学习本章后,不仅可以进一步认识_________,而且还可以了解一些几何中研究问题的____________________.
2. 三角形:由不在同一条直线的三条线段_______________所组成的图形
叫做三角形.如图,线段_______________________是三角形的边,点____________是三角形的____点.∠A、∠B、∠C(在图中画弧)是三角形的______.三角形的内角简称三角形的角. 顶点是A、B、C的三角形,记作 _______.读作三角形ABC.△ABC的边有时也用小写字母a. b. c来表示.要求:顶点A所对的边BC用小写字母a表示,顶点B所对的边AC用小写字母b表示,顶点C所对的边AB用小写字母c表示.(在上图中标出a b c)
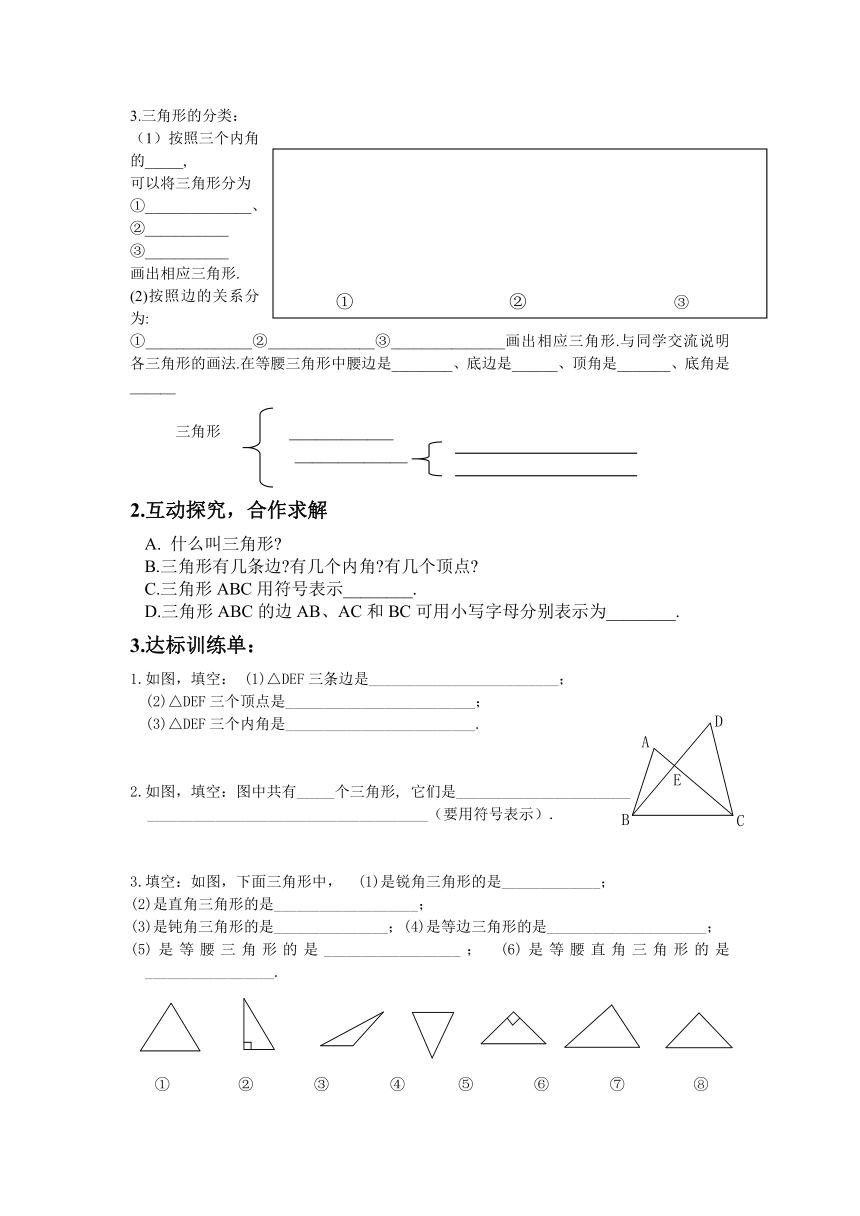
3.三角形的分类:
(1)按照三个内角的_____,
可以将三角形分为
①______________、
②___________
③___________
画出相应三角形.
(2)按照边的关系分为:
①______________②______________③_______________画出相应三角形.与同学交流说明各三角形的画法.在等腰三角形中腰边是________、底边是______、顶角是_______、底角是______
三角形 ____________
_____________
2.互动探究,合作求解
A. 什么叫三角形
B.三角形有几条边 有几个内角 有几个顶点
C.三角形ABC用符号表示________.
D.三角形ABC的边AB、AC和BC可用小写字母分别表示为________.
3.达标训练单:
1.如图,填空: (1)△DEF三条边是_________________________;
(2)△DEF三个顶点是_________________________;
(3)△DEF三个内角是_________________________.
2.如图,填空:图中共有_____个三角形, 它们是_______________________
_____________________________________(要用符号表示).
3.填空:如图,下面三角形中, (1)是锐角三角形的是_____________;
(2)是直角三角形的是___________________;
(3)是钝角三角形的是_______________;(4)是等边三角形的是_____________________;
(5)是等腰三角形的是__________________; (6)是等腰直角三角形的是_________________.
① ② ③ ④ ⑤ ⑥ ⑦ ⑧
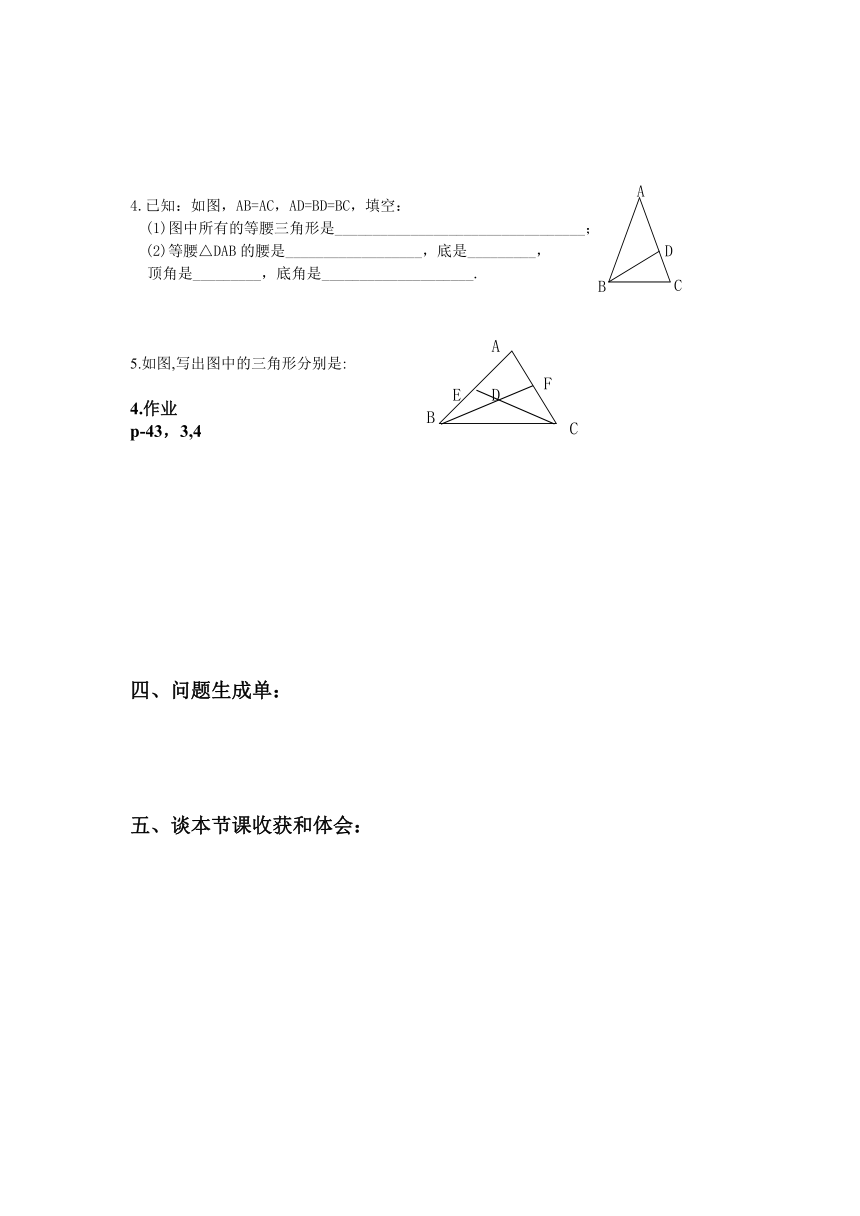
4.已知:如图,AB=AC,AD=BD=BC,填空:
(1)图中所有的等腰三角形是_________________________________;
(2)等腰△DAB的腰是__________________,底是_________,
顶角是_________,底角是____________________.
5.如图,写出图中的三角形分别是:
4.作业
p-43,3,4
四、问题生成单:
五、谈本节课收获和体会:
课题:7.1.1三角形的边(2)
一、教材分析:
(一)学习目标:
1.经历结论“三角形两边之和大于第三边”的探究过程,给出三条线段,会判断它们能否构成三角形.
2.根据三角形三边的关系,会求等腰三角形的周长.
(二)学习重点和难点:
1.重点:结论的探究与运用.
2.难点:利用三角形三边的关系,求等腰三角形的周长.
二、教学过程:
1.任务导读单:(阅读P64—65页回答下列问题)
1.P64探究,你的答案是:_______________________________________________.你有几种理论(别忘记书中有一理论)可以说明其中原因(与同组同学交流说明,讲清你的理论,说服你的同学.)
2.由P64探究,我们得出新的道理:____________________________________.
3.研读例题,(1)题若:设腰边长为ycm,则底边长为____cm.所列方程为:__________
(2)说明小(2)题中有几种可能 为什么 _________________________________
4.两条线段的和统统要________第三条线段,这样的三条段线段就能组成三角形.而只要有这么两条线段的和小于或者等于第三条线段,那么这三条线段就组______(填成或不成)三角形.
2.互动探究,合作求解:
A.在用一个三角形中,任意两边之和与第三边有什么关系
B.在同一个三角形中,任意两边之差与第三边有什么关系
C.三角形三边有怎样的不等关系
通过动手实验同学们可以得到哪些结论
三角形的任意两边之和大于第三边;任意两边之差小于第三边.
3、达标训练单:
1.有下列长度的三条线段能否组成三角形?为什么?
(1)3,5,8; (2)5,6,10; (3)5,6,7. (4)5,6,12
2.有下列长度的三条线段能不能组成三角形?(填“能”或“不能”)
(1)5,6,7; ( )(2)9,6,2; ( ) (3)3,6,3. ( )
3.辨析题:有三条线段a、b、c,a+b>c,扎西认为:这三条线段能组成三角形.你同意扎西的看法吗?为什么?(给同学说理)
4. (1)已知等腰三角形的一边等于7,一边等于9,它的周长等于_____________;
(2)已知等腰三角形的一边等于3,一边等于6,它的周长等于_____________.
5.填空:(1)若等腰三角形的一边长为6,一边长为10,则另一边长为_____________;
(2)若等腰三角形的一边长为6,一边长为13,则另一边长为______________;
(3)若等腰三角形的周长为29,一边长为7,则另两边长为________________.
6.一个三角形的三个内角中 ( )
A .至少有一个钝角 B.至少有一个直角 C.至多有一个锐角 D. 至少有两个锐角
7.下列长度的三条线段能组成三角形的是 ( )
A、 3,4,8 B、 5,6,11 C、 1,2,3 D、 5,6,10
8.关于三角形的边的叙述正确的是 ( )
A、 三边互不相等 B、任意两边之和一定大于第三边
C、 至少有两边相等 D、 最多有两边相等
9.图中有三角形的个数为 ( )
A、 4个 B、 6个 C、 8个 D、 10个
10.下列每组数分别是三根小木棒的长度,
用它们能摆成三角形的是()
A 、3㎝,4㎝,8㎝ B、 8㎝,7㎝,15㎝
C、 13㎝,12㎝,20㎝ D、5㎝, 5㎝,11㎝
4.作业
p-43,3,
三、问题生成单:
课题7.1.2三角形的高.中线与角平分线
7.1.3三角形的稳定性
一、教材分析:
(一)学习目标:
1.能说出什么是三角形的高、中线、角平分线,
2.会画出任意三角形的高、中线、角平分线.
3.知道三角形具有稳定性,四边形没有稳定性,会判断一些简单图形的稳定性.
(二)学习重点和难点:
1.重点:三角形的高、中线、角平分线的概念、三角形的稳定性.
2.难点:画钝角三角形的高、判断图形的稳定性.
二、教学过程:
1.任务导读单:阅读P65—68页回答下列问题:
1.阅读相关内容与同学交流什么是高、中线、角平分线,并说明如何画出各注意什么
2.完成P66页练习题。
3.说明三角形的________性和四边形的____________性,实际生活中有哪些应用
4.完成P68页练习题.
2.互动探究,合作求解
A.什么叫三角形的高 三角形的高与垂线有何区别和联系
B. 什么叫三角形的中线 连结两点的线段与过两点的直线有何区别和联系
C.什么叫三角形的角平分线 三角形的角平分线与角平分线有何区别和联系
3.达标训练单:
1.画出①、②、③三个△ABC各边的高,并说明是哪条边的高.
① ② ③
AB边上的高是线段____ AB边上的高是线段____ AB边上的高是线段____
BC边上的高是_________ BC边上的高是_________ BC边上的高是_________
AC边上的高是_________ AC边上的高是_________ AC边上的高是_________
2. 画出①、②、③三个△ABC各边的中线,并说明是哪条边的中线.
① ② ③
AB边上的中线是线段____ AB边上的中线是线段____ AB边上的中线是线段____
BC边上的中线是_________ BC边上的中线是_________ BC边上的中线是_________
AC边上的中线是________ AC边上的中线是_________ AC边上的中线是_________
写出图中有有相等关系的线段:___________________________________________________
3. 画出△ABC各角的角平分线, 并说明是哪角的角平分线.
∠ABC的角平分线是线段____ ∠ABC的角平分线是线段____
∠BAC的角平分线是__________ ∠BAC的角平分线是__________
∠ACB的角平分线是___________ ∠ACB的角平分线是___________
写出图中所有相等关系的角: _________________________________________________________
__________________________________________________________________________________
4.如图,AD、AE、CF分别是△ABC的中线、角平分线和高,则:
(1)BD=______=________; (2)BC=2_______=2_______;
(3)∠BAE=_______=_______;(4)∠BAC=2_______=2_______;(5)_______=________=90°.
5.如图,画出△ABC的中线AD、角平分线BE、高CF.
6.如图,画出△ABC的三条中线,三条中线相交于一点吗?_______________________
7.如图,画出△ABC的三条角平分线,三条角平分线相交于一点吗?________________
8.下列图形中具有稳定性有 ( )
A、 2个 B、 3个
C、 4个 D、 5个
四、问题生成单:
课题:7.2.1三角形的内角(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.经历用拼角的方法得到结论的过程,知道三角形内角和等于180°.
2.会在简单图形中运用结论求内角.
(二)学习重点和难点:
1.重点:三角形内角和及运用.
2.难点:列方程求内角.
二、问题导读单:阅读P72—74页回答下列问题:
1. 按P72页”探究”实验操作,拼合一平角,回答探究问题.
2. 结论:三角形三个内角的和等于_______°(_________定理)
3.如图,填空:(1)∠1=______; (2)∠1=______;(3)∠1=______,∠2=______;
第(1)题图 第(2)题图 第(3)题图 第(4)题图 第(5)题图
(4)∠1=______,∠2=______; (5)∠1=______.
4.判断正误:(1)一个三角形的三个内角中,可能有两个直角; ( )
(2)一个三角形的三个内角中,最多有一个钝角. ( )
三、问题训练单:
5. 已知:在△ABC中,∠B=∠C=2∠A. 求∠A、∠B、∠C的度数.
6.在△ABC中,若∠A=800,∠C=200,则∠B= ___ 0, 若∠A=800,∠B=∠C,则∠C= 0
7.已知:在△ABC中,∠A﹕∠B﹕∠C=4﹕1﹕5.求∠A、∠B、∠C的度数.
解:设∠B为x°,则∠A为______,∠C为_______,
根据题意,列方程得________________________,
解得x=______.
所以,∠A=_______,∠B=________,∠C=________.
8.已知:在△ABC中,∠A=∠B=∠C.求∠A、∠B、∠C的度数.
9.已知△ABC的三个内角的度数之比∠A:∠B:∠C=1:3:5,
则∠B= 0,∠C= 0
10.如图,在△ABC中,∠BAC=600,∠B=450,
AD是△ABC的一条角平分线,则∠DAC= 0,∠ADB= 0
11*.如图,∠1=∠2=300,∠3=∠4,∠A=800,则 ,
12*.求出下列图中的值:
13*.如图,则
∠1= 0,∠2= 0,∠3= 0
14*.在△ABC中,∠A=900,∠B-∠C=240,
那么∠B= 0,∠C= 0
四、问题生成单:
五、谈本节课收获和体会:
课题:7.2.1三角形的内角(2) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.结合三角形内角和定理的证明,初步理解证明的必要性.
2.理解三角形内角和定理的证明过程,会证明三角形内角和定理.
3.会在较简单图形中综合运用三角形内角和定理求角度
二、教学重点和难点
1.重点:三角形内角和定理的证明过程.
2.难点:理解证明的必要性.
(二)学习重点和难点:
二、问题导读单:阅读P72—74页回答下列问题:
1. 证明:三角形三个内角和等于180°
(细读P73页示例按给定图写出已知、求证和证明过程)
已知:__________
求证:_______________________
证明:如图,过点A作________,使________.
因为___________,
所以∠____=∠___,∠___=∠_____(两直线平行,__________相等).
又因为∠___+∠___+∠_____=180°(_______定义),
所以∠____+∠____ +∠_____=180°(等量代换).
即∠A+∠B+∠C=180°.
从以上推导过程要以看出,证明是由_____________出发,经过一步步的_____,最后推出__________正确的过程.
2.完成下面的证明过程:
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证明:如图,过点C作直线l,使l∥AB.
因为l∥AB,
所以∠A=∠____,∠B=∠____( ).
又因为∠1+∠2+∠3=180°(平角定义).
所以∠_____+∠______+∠3=180°(等量代换).
即∠A+∠B+∠C=180°.
3.认真研读P74页例题,说明:一般情况说明方位角时用”___(或 )偏___(或____)多少度.”形式.题中”从C岛看A,B两岛的视角_______“改为”从A岛看C,B两岛的则视角为_______”..在解答本题中应用了哪些数学原理 _________________________________________________________
4.如图,在△ABC中,D是BC边上一点,
∠B=32°,∠C=65°,∠BAD=49°,
求∠CAD、∠CDA的度数.
解:在△ABC中,
∠BAC=__________________=_________________=83°.
∠CAD=____________=______________=______.
在△ACD中,
∠CDA=___________________________________________________.
三、问题训练单:
5.如图,∠CAD=30°,∠CBD=45°,则∠ACB=________°.
6.如图,BD是△ABC的角平分线,∠A=70°,∠C=60°,则∠CBD=___°,∠BDC=___°.
7*.在△ABC中,∠A=∠C=∠ABC, BD是角平分线,求∠A及∠BDC的度数.
8*.如图,已知∠1=∠2,∠3=∠4,∠A=1000,求的值。
四、问题生成单:
课题:7.2.2三角形的外角(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.知道什么是三角形的外角,会在简单图形中识别三角形的外角.
2.经历探究外角与它不相邻的两个内角的关系的过程,会证明和运用结论.
3.知道三角形的一个外角大于与它不相邻的任何一个内角.
(二)学习重点和难点:
1.重点:外角的概念,结论的探究和运用.
2.难点:结论的探究和证明.
二、问题导读单:阅读P74—75页回答下列问题:
1.三角形的外角:如图, ∠______就是△ABC的一个外角,也可以说∠____是∠____的外角. 说明此角是如何形成的 _________________________________________
分析说明: ∠ACD是∠ACB的一个_____角,也是∠ACB的一个_____角.故有两角关系为:_____________________________
2.判断图中∠1是不是△ABC的外角:_______________
3.如图,(1)∠1、∠2都是△ABC的外角吗?________________
(2)△ABC共有多少个外角?___________________
请在图中标出△ABC的其它外角.
4.探究题:如图,△ABC中,∠A=70°,∠B=60°,
∠ACD是△ABC的一个外角,
(1)则∠ACB=_____°, ∠ACD=_____°;
(2)∠ACD与∠A、∠B有什么关系?
由此你发现了什么数学结论?
______________________________________________
______________________________________________________________________
5.细心分析研究“P74页探究”回答有关问题.(与同组同学交流)
由探究得到的结论:结论1______________________________________________
结论2______________________________________________________(外角两性质)
三、问题训练单:
6.填空:求出下列各图中∠1的度数.
(1)如图,∠1=______;(2)如图,∠1=______;(3)如图,∠1=______;
(4)如图,∠1=______;(5)如图,∠1=______;(6)如图,∠1=______.
7.判断正误:对的有______,错的有_________.
(1)三角形的一个外角等于两个内角的和.
(2)三角形的一个外角减去它的一个不相邻的内角,等于它的另一个不相邻的内角. (3)三角形的一个外角大于与它不相邻的一个内角.
8.完成下面的证明过程:
如何证明“三角形的一个外角等于与它不相邻的两个内角的和”?
已知:如图,∠ACD是△ABC的一个外角.
求证:∠ACD=∠A+∠B.
证明:因为∠A+∠B+∠C=180°(三角形内角和定理),
所以∠A+∠B=180°-__________.
又因为∠ACD=180°-__________(平角的定义),
所以__________=____________.
四、问题生成单:
课题:7.2.2三角形的外角(2) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
会综合运用内角和定理、外角性质求角度.
(二)学习重点和难点:
1.重点:综合运用内角和定理、外角性质求角度.
2.难点:综合运用内角和定理、外角性质求角度.
二、问题导读单:阅读P74—75页回答下列问题:
1.写出三角形外角的两条性质: __________________________________________
__________________________________________________________________
2. 已知:如图,∠1=30°,∠2=50°,∠3=45°,
则(1)∠4=______°;(2)∠5=______°.
3.已知:如图∠1=40°,∠2=∠3,则
(1)∠4=______°;(2)∠2=______°.
4.如图,AB∥CD,∠B=55°,∠C=40°,则
(1)∠D=______°;(2)∠1=______°.
5. 例2.如图,∠BAE,∠CBF,
∠ACD是△ABC的三个外角,
它们的和是多少?
解:因为∠BAE=∠__+∠____,
∠CBF=∠__+∠___,
∠ACD=__________,
所以∠BAE+∠CBF+∠ACD
=(∠__+∠___)+(________)+(___________)
=2(∠1+_________)=2×180°=360°.
从例2.我们可以得到一个数学结论: 三角形________________________________.
三、问题训练单:
6 已知:如图,∠B=30°,∠C=65°,∠BAD=50°,
求∠CAD的度数.
解:在△ABC中,∠ADC=∠____+∠___=____°+___°=_______.
在△ADC中,∠CAD=180°-_____________
=180°-_____________=_________.
7.已知:如图,在△ABC中,AD是BC边上的高,
∠BAC=80°,∠C=40°,则∠BAD=________°.
8.已知:如图,BD是△ABC的角平分线,
∠A=100°,∠C=30°,则∠ADB=________°.
9.*如图,AD、BE分别是△ABC的高和
角平分线,∠BAC=100°,∠C=30°,则∠1=________°.
10*.△ABC中,∠B=∠A+100,∠C=∠B+200,
求△ABC各内角的度数
11*已知,如图,AB∥CD,AE平分∠BAC,
CE平分∠ACD,求∠E的度数
四、问题生成单:
五、谈本节课收获和体会:
课题:7.3.1多边形(1) 月 日 班级: 姓名:
一、教材分析:∠①②③
(一)学习目标:
1.能说出什么是多边形、n边形、多边形的内角、多边形的外角、多边形的对角线、正多边形.
2.经历探究从n边形的一个顶点出发,可以画出n-3条对角线,它们把n边形分成n-2个三角形的过程,培养合情推理能力.
(二)学习重点和难点:
1.重点:与多边形有关的概念.
2.难点:探究过程.
二、问题导读单:阅读P79—81页回答下列问题:
1.在平面内,由三条线段___________相接组成的图形叫做三角形.由四条线段首尾顺次相接组成的,这种图形应该叫做_______形,类似地,如果一个多边形由___条线段组成,那么这个多边形就叫做______________.填写下图是几边形.
2. 三角形有内角和外角,同样,多边形也有内角和外角.
如五边形ABCDE中内角有______________________
画出∠BAE的两个外角,
3. 多边形的对角线,画出五边形对角线,并写出对角线:
___________________________________
4.凸多边形与不是凸多边形的区别:________________________________________
_______________________________________________________________________
5.正多边形,_______________________的多边形,叫做正多边形.
6.完成P81页练习.
三、问题训练单:
7.判断正误:对的有_______,错的有___________.
(1)∠1是四边形ABCD的外角 (2)∠2是四边形ABCD的外角;
(3)∠3是四边形ABCD的外角; (4)∠4是四边形ABCD的外角;
(5)∠5是四边形ABCD的外角.
8. 画出五边形中∠BAE的一个外角∠1.
这个内角与这个外角有什么关系?
从中得出结论是:
______________________________________
________________________________________
9*.画出下列多边形的全部对角线,并填空:
三角形共有_______条对角线,四边形共有_______条对角线,
五边形共有_______条对角线,
六边形共有_______条对角线.
10*合做探究题
(1)如图,从五边形的同一个顶点出发,
一共可以画2条对角线,这2条对角线
把五边形分成3个三角形;
(2)如图,从六边形的同一个顶点出发,
一共可以画______条对角线,这些对角
线把六边形分成______个三角形;(3)从十边形的同一个顶点出发,一共可以画______条对角线,这些对角线把十边形分成______个三角形;(4)从一百边形的同一个顶点出发,一共可以画______条对角线,这些对角线把一百边形分成______个三角形;(5)从n边形的同一个顶点出发,一共可以画______条对角线,这些对角线把n边形分成______个三角形.
四、问题生成单:
课题:7.3.2多边形的内角和(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.经历探究多边形内角和公式,体会转化思想,体会从特殊到一般的认识问题的方法.
2.会简单运用多边形内角和公式.
(二)学习重点和难点:
1.重点:探究多边形内角和公式.
2.难点:探究多边形内角和时,如何把多边形转化成三角形.
二、问题导读单:阅读P81—83页回答下列问题:
1.细心研读P81页“探究”,三角形的内角和是_______,
正方形、长方形的内角和等于______度(因为___________
______________________________________________),
那任意四边形ABCD的内角和又等于多少 利用左图,连辅助线进行说明.
2.探究题:
(1)如图,从五边形的同一个顶点出发,一共可以画______条对角线,这些对
角线把五边形分成了______个三角形,所以五边形的内角和等于_____×180°.
(2)如图,从六边形的同一个顶点出发,一共可以画_____条对角线,这些对
角线把六边形分成了_____个三角形,所以六边形的内角和等于____×180°.
(3)从n边形的同一个顶点出发,一共可以画________条对角线,这些对角
线把n边形分成了_______个三角形,所以n边形的内角和等于_____×180°.
我们就得出了多边形内角和公式:n边形内角和 =___________________
3. 根据多边形内角和公式填空: 四边形的内角和=_______°,五边形的内角和=_______°,
六边形的内角和=_______°,七边形的内角和=_______°,八边形的内角和=_______°.
4.研读P82页例1,说明在进行本题目的解答过程中应用了的数学原理:____________
_____________________________________________________.完成P83页练习中1题.
三、问题训练单:
5.一个多边形的内角和为720°,那么它是________边形.
6.一个多边形每一个内角等于144°,则其边数是________.
7.下列角度中,不能成为多边形内角和的是( )
A. 600° B. 420° C. 900° D. 1800°
8.如果五边形的三个内角是直角,另两个内角都为n°,则n的值为 ( )
A.105 B.120 C.125 D.135
9.一个四边形的内角中,钝角最多有( ) A.一个 B.两个 C.三个 D.四个
10. 一个四边形四个内角∠A、∠B、∠C、∠D的度数比是2:3:4:3,求这个四边形的四个内角.
分析与简解:我们从∠A、∠B、∠C、∠D的度数比是2:3:4:3,所以如果我们设∠A的度数为2x则∠B、∠C、∠D的度数为___,____,_____.根据题意,列方程:___________________
解得x=30.所以,∠A=2x°=2×____°=_____°.类似,∠B =_______________________、
∠C =____________________________、∠D= _____________________________________
11.四边形ABCD中若∠A +∠B +180° 且: ∠B:∠C:∠D =1:2:3则∠A=___________
12.一个五边形剪去一个角后,剩下的内角和是多少度:________________________________
13.如果一个多边形除了一个内角外,其余各内角这和为1190°,则这个内角为_________度,是一个__________边形.
14.一个多边形截去一个角(不过顶点)后,所形成的一个多边形的内角和是2520°,那么原多边形的边数是 ( ) A.13 B.15 C.17 D.19
四、问题生成单:
课题:7.3.2多边形的内角和(2) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.经历探究多边形外角和的结论,知道多边形外角和等于360°.
2.会运用多边形内角和公式、多边形外角和结论.
(二)学习重点和难点:
1.重点:外角和及运用.
2.难点:探究多边形外角和结论.
二、问题导读单:阅读P81—83页回答下列问题:
1. (1)十二边形的内角和等于________°;
(2)一个多边形的内角和等于2160°,这个多边形是______边形.
2.如图,∠1是△ABC的_______,∠2、∠3也是△ABC的_____.△ABC的外角和∠1+∠2+∠3等于_____度,△ABC的外角和∠1+∠2+∠3等于______°.
3.细心研读P82页例2,回答分析问题,把答案相应写出:
(1)_________________________________________________________________
(2)__________________________________________________________________
(3)_________________________________________________________________
4.思考回答P83页”探究”.______________________________________________
5.得出关于多边形的外角性质结论: ________________________________________
6.图7.3-12中问题,进行实验体会说明的结论是:_____________________________
三、问题训练单:
7.填表:
多边形的边数 3 4 5 6 7 8 12
内角和
外角和
8.填空:如果一个多边形的内角和与外角和相等,那么这个多边形是______边形.
9.填空:如果一个多边形的各外角都等于60°,那么这个多边形是______边形.
10.填空:如果一个多边形的各内角都等于120°,那么这个多边形是______边形.
11.一个多边形的内角和是外角和的2.5倍,它是几边形?
解:设这个多边形为n边形. - - - - 注意学习解题格式
根据题意,列方程得(_______)·180=_______×360.
解得 n=____.
答:这个多边形是_____边形.
12.求下列图中x值
答案:
(1)X=
(2)X=
13.四边形的内角和是_________,外角和是___________
14.一个多边形的每一个外角为18°,则它是一个______边形.
15.当多边形的边数增加1时,其内角和增加______度,外角和增加___度.
16一个正多边形的每个外角都是72°,则这个多边形是__________边形.
17.每个内角都为144°的多边形为______边形.
18.若多边形的内角和等于外角的3倍,则这个多边形的边是______.
19.四边形中,如果有一组对角都是直角,那么另一组对角可能( )
A.都是钝角 B.都是锐角 C.是一个锐角,一个钝角. D. 是一个锐角,一个直角
20**.若一个多边形的各内角都相等,则一个内角与一个外角的度数之比不可能是( ) A.2:1 B.1:1 C.5:2 D.5:4
21**一个多边形的内角中,锐角的个数最多有 ( )
A.3个 B.4个 C.5个 D.6个
22**若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( ) A.90° B.105° C.130° D.120°
四、问题生成单:
五、谈本节课收获和体会:
① ② ③
① ② ③
A
B
C
D
E
F
11题图
9题图
10题图
10题图
11题图
13题图
7题图
6题图
5题图
第6题(2)
第6题(3)
第6题(1)
第6题(4)
第6题(6)
第6题(5)
第3题图
第2题图
第5题图
第4题图
第2题图
________
________
________
________
________
80 °
120 °
75 ° x°
150 °2x°
120 °
x°
课题:7.1.1三角形的边(1)
一、教材分析:
(一)学习目标:
1.知道什么是三角形及其边、顶点、角,会用符号表示三角形.
2.知道什么是锐角三角形、直角三角形、钝角三角形,会按角将三角形分类.
3.知道什么是等腰三角形、等边三角形,会按边将三角形分类.
(二)学习重点和难点:
1.重点:三角形及其有关的概念、三角形的分类.
2.难点:按边将三角形分类.
二、教学过程:
1.任务导读单:阅读P62—64页回答下列问题:
1.三角形是最简单的______图形,也是认识许多其他图形的________.本章将学习与三角形有关的_____和_____,并借助三角形中三个角的和等于____探究________________.学习本章后,不仅可以进一步认识_________,而且还可以了解一些几何中研究问题的____________________.
2. 三角形:由不在同一条直线的三条线段_______________所组成的图形
叫做三角形.如图,线段_______________________是三角形的边,点____________是三角形的____点.∠A、∠B、∠C(在图中画弧)是三角形的______.三角形的内角简称三角形的角. 顶点是A、B、C的三角形,记作 _______.读作三角形ABC.△ABC的边有时也用小写字母a. b. c来表示.要求:顶点A所对的边BC用小写字母a表示,顶点B所对的边AC用小写字母b表示,顶点C所对的边AB用小写字母c表示.(在上图中标出a b c)
3.三角形的分类:
(1)按照三个内角的_____,
可以将三角形分为
①______________、
②___________
③___________
画出相应三角形.
(2)按照边的关系分为:
①______________②______________③_______________画出相应三角形.与同学交流说明各三角形的画法.在等腰三角形中腰边是________、底边是______、顶角是_______、底角是______
三角形 ____________
_____________
2.互动探究,合作求解
A. 什么叫三角形
B.三角形有几条边 有几个内角 有几个顶点
C.三角形ABC用符号表示________.
D.三角形ABC的边AB、AC和BC可用小写字母分别表示为________.
3.达标训练单:
1.如图,填空: (1)△DEF三条边是_________________________;
(2)△DEF三个顶点是_________________________;
(3)△DEF三个内角是_________________________.
2.如图,填空:图中共有_____个三角形, 它们是_______________________
_____________________________________(要用符号表示).
3.填空:如图,下面三角形中, (1)是锐角三角形的是_____________;
(2)是直角三角形的是___________________;
(3)是钝角三角形的是_______________;(4)是等边三角形的是_____________________;
(5)是等腰三角形的是__________________; (6)是等腰直角三角形的是_________________.
① ② ③ ④ ⑤ ⑥ ⑦ ⑧
4.已知:如图,AB=AC,AD=BD=BC,填空:
(1)图中所有的等腰三角形是_________________________________;
(2)等腰△DAB的腰是__________________,底是_________,
顶角是_________,底角是____________________.
5.如图,写出图中的三角形分别是:
4.作业
p-43,3,4
四、问题生成单:
五、谈本节课收获和体会:
课题:7.1.1三角形的边(2)
一、教材分析:
(一)学习目标:
1.经历结论“三角形两边之和大于第三边”的探究过程,给出三条线段,会判断它们能否构成三角形.
2.根据三角形三边的关系,会求等腰三角形的周长.
(二)学习重点和难点:
1.重点:结论的探究与运用.
2.难点:利用三角形三边的关系,求等腰三角形的周长.
二、教学过程:
1.任务导读单:(阅读P64—65页回答下列问题)
1.P64探究,你的答案是:_______________________________________________.你有几种理论(别忘记书中有一理论)可以说明其中原因(与同组同学交流说明,讲清你的理论,说服你的同学.)
2.由P64探究,我们得出新的道理:____________________________________.
3.研读例题,(1)题若:设腰边长为ycm,则底边长为____cm.所列方程为:__________
(2)说明小(2)题中有几种可能 为什么 _________________________________
4.两条线段的和统统要________第三条线段,这样的三条段线段就能组成三角形.而只要有这么两条线段的和小于或者等于第三条线段,那么这三条线段就组______(填成或不成)三角形.
2.互动探究,合作求解:
A.在用一个三角形中,任意两边之和与第三边有什么关系
B.在同一个三角形中,任意两边之差与第三边有什么关系
C.三角形三边有怎样的不等关系
通过动手实验同学们可以得到哪些结论
三角形的任意两边之和大于第三边;任意两边之差小于第三边.
3、达标训练单:
1.有下列长度的三条线段能否组成三角形?为什么?
(1)3,5,8; (2)5,6,10; (3)5,6,7. (4)5,6,12
2.有下列长度的三条线段能不能组成三角形?(填“能”或“不能”)
(1)5,6,7; ( )(2)9,6,2; ( ) (3)3,6,3. ( )
3.辨析题:有三条线段a、b、c,a+b>c,扎西认为:这三条线段能组成三角形.你同意扎西的看法吗?为什么?(给同学说理)
4. (1)已知等腰三角形的一边等于7,一边等于9,它的周长等于_____________;
(2)已知等腰三角形的一边等于3,一边等于6,它的周长等于_____________.
5.填空:(1)若等腰三角形的一边长为6,一边长为10,则另一边长为_____________;
(2)若等腰三角形的一边长为6,一边长为13,则另一边长为______________;
(3)若等腰三角形的周长为29,一边长为7,则另两边长为________________.
6.一个三角形的三个内角中 ( )
A .至少有一个钝角 B.至少有一个直角 C.至多有一个锐角 D. 至少有两个锐角
7.下列长度的三条线段能组成三角形的是 ( )
A、 3,4,8 B、 5,6,11 C、 1,2,3 D、 5,6,10
8.关于三角形的边的叙述正确的是 ( )
A、 三边互不相等 B、任意两边之和一定大于第三边
C、 至少有两边相等 D、 最多有两边相等
9.图中有三角形的个数为 ( )
A、 4个 B、 6个 C、 8个 D、 10个
10.下列每组数分别是三根小木棒的长度,
用它们能摆成三角形的是()
A 、3㎝,4㎝,8㎝ B、 8㎝,7㎝,15㎝
C、 13㎝,12㎝,20㎝ D、5㎝, 5㎝,11㎝
4.作业
p-43,3,
三、问题生成单:
课题7.1.2三角形的高.中线与角平分线
7.1.3三角形的稳定性
一、教材分析:
(一)学习目标:
1.能说出什么是三角形的高、中线、角平分线,
2.会画出任意三角形的高、中线、角平分线.
3.知道三角形具有稳定性,四边形没有稳定性,会判断一些简单图形的稳定性.
(二)学习重点和难点:
1.重点:三角形的高、中线、角平分线的概念、三角形的稳定性.
2.难点:画钝角三角形的高、判断图形的稳定性.
二、教学过程:
1.任务导读单:阅读P65—68页回答下列问题:
1.阅读相关内容与同学交流什么是高、中线、角平分线,并说明如何画出各注意什么
2.完成P66页练习题。
3.说明三角形的________性和四边形的____________性,实际生活中有哪些应用
4.完成P68页练习题.
2.互动探究,合作求解
A.什么叫三角形的高 三角形的高与垂线有何区别和联系
B. 什么叫三角形的中线 连结两点的线段与过两点的直线有何区别和联系
C.什么叫三角形的角平分线 三角形的角平分线与角平分线有何区别和联系
3.达标训练单:
1.画出①、②、③三个△ABC各边的高,并说明是哪条边的高.
① ② ③
AB边上的高是线段____ AB边上的高是线段____ AB边上的高是线段____
BC边上的高是_________ BC边上的高是_________ BC边上的高是_________
AC边上的高是_________ AC边上的高是_________ AC边上的高是_________
2. 画出①、②、③三个△ABC各边的中线,并说明是哪条边的中线.
① ② ③
AB边上的中线是线段____ AB边上的中线是线段____ AB边上的中线是线段____
BC边上的中线是_________ BC边上的中线是_________ BC边上的中线是_________
AC边上的中线是________ AC边上的中线是_________ AC边上的中线是_________
写出图中有有相等关系的线段:___________________________________________________
3. 画出△ABC各角的角平分线, 并说明是哪角的角平分线.
∠ABC的角平分线是线段____ ∠ABC的角平分线是线段____
∠BAC的角平分线是__________ ∠BAC的角平分线是__________
∠ACB的角平分线是___________ ∠ACB的角平分线是___________
写出图中所有相等关系的角: _________________________________________________________
__________________________________________________________________________________
4.如图,AD、AE、CF分别是△ABC的中线、角平分线和高,则:
(1)BD=______=________; (2)BC=2_______=2_______;
(3)∠BAE=_______=_______;(4)∠BAC=2_______=2_______;(5)_______=________=90°.
5.如图,画出△ABC的中线AD、角平分线BE、高CF.
6.如图,画出△ABC的三条中线,三条中线相交于一点吗?_______________________
7.如图,画出△ABC的三条角平分线,三条角平分线相交于一点吗?________________
8.下列图形中具有稳定性有 ( )
A、 2个 B、 3个
C、 4个 D、 5个
四、问题生成单:
课题:7.2.1三角形的内角(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.经历用拼角的方法得到结论的过程,知道三角形内角和等于180°.
2.会在简单图形中运用结论求内角.
(二)学习重点和难点:
1.重点:三角形内角和及运用.
2.难点:列方程求内角.
二、问题导读单:阅读P72—74页回答下列问题:
1. 按P72页”探究”实验操作,拼合一平角,回答探究问题.
2. 结论:三角形三个内角的和等于_______°(_________定理)
3.如图,填空:(1)∠1=______; (2)∠1=______;(3)∠1=______,∠2=______;
第(1)题图 第(2)题图 第(3)题图 第(4)题图 第(5)题图
(4)∠1=______,∠2=______; (5)∠1=______.
4.判断正误:(1)一个三角形的三个内角中,可能有两个直角; ( )
(2)一个三角形的三个内角中,最多有一个钝角. ( )
三、问题训练单:
5. 已知:在△ABC中,∠B=∠C=2∠A. 求∠A、∠B、∠C的度数.
6.在△ABC中,若∠A=800,∠C=200,则∠B= ___ 0, 若∠A=800,∠B=∠C,则∠C= 0
7.已知:在△ABC中,∠A﹕∠B﹕∠C=4﹕1﹕5.求∠A、∠B、∠C的度数.
解:设∠B为x°,则∠A为______,∠C为_______,
根据题意,列方程得________________________,
解得x=______.
所以,∠A=_______,∠B=________,∠C=________.
8.已知:在△ABC中,∠A=∠B=∠C.求∠A、∠B、∠C的度数.
9.已知△ABC的三个内角的度数之比∠A:∠B:∠C=1:3:5,
则∠B= 0,∠C= 0
10.如图,在△ABC中,∠BAC=600,∠B=450,
AD是△ABC的一条角平分线,则∠DAC= 0,∠ADB= 0
11*.如图,∠1=∠2=300,∠3=∠4,∠A=800,则 ,
12*.求出下列图中的值:
13*.如图,则
∠1= 0,∠2= 0,∠3= 0
14*.在△ABC中,∠A=900,∠B-∠C=240,
那么∠B= 0,∠C= 0
四、问题生成单:
五、谈本节课收获和体会:
课题:7.2.1三角形的内角(2) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.结合三角形内角和定理的证明,初步理解证明的必要性.
2.理解三角形内角和定理的证明过程,会证明三角形内角和定理.
3.会在较简单图形中综合运用三角形内角和定理求角度
二、教学重点和难点
1.重点:三角形内角和定理的证明过程.
2.难点:理解证明的必要性.
(二)学习重点和难点:
二、问题导读单:阅读P72—74页回答下列问题:
1. 证明:三角形三个内角和等于180°
(细读P73页示例按给定图写出已知、求证和证明过程)
已知:__________
求证:_______________________
证明:如图,过点A作________,使________.
因为___________,
所以∠____=∠___,∠___=∠_____(两直线平行,__________相等).
又因为∠___+∠___+∠_____=180°(_______定义),
所以∠____+∠____ +∠_____=180°(等量代换).
即∠A+∠B+∠C=180°.
从以上推导过程要以看出,证明是由_____________出发,经过一步步的_____,最后推出__________正确的过程.
2.完成下面的证明过程:
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证明:如图,过点C作直线l,使l∥AB.
因为l∥AB,
所以∠A=∠____,∠B=∠____( ).
又因为∠1+∠2+∠3=180°(平角定义).
所以∠_____+∠______+∠3=180°(等量代换).
即∠A+∠B+∠C=180°.
3.认真研读P74页例题,说明:一般情况说明方位角时用”___(或 )偏___(或____)多少度.”形式.题中”从C岛看A,B两岛的视角_______“改为”从A岛看C,B两岛的则视角为_______”..在解答本题中应用了哪些数学原理 _________________________________________________________
4.如图,在△ABC中,D是BC边上一点,
∠B=32°,∠C=65°,∠BAD=49°,
求∠CAD、∠CDA的度数.
解:在△ABC中,
∠BAC=__________________=_________________=83°.
∠CAD=____________=______________=______.
在△ACD中,
∠CDA=___________________________________________________.
三、问题训练单:
5.如图,∠CAD=30°,∠CBD=45°,则∠ACB=________°.
6.如图,BD是△ABC的角平分线,∠A=70°,∠C=60°,则∠CBD=___°,∠BDC=___°.
7*.在△ABC中,∠A=∠C=∠ABC, BD是角平分线,求∠A及∠BDC的度数.
8*.如图,已知∠1=∠2,∠3=∠4,∠A=1000,求的值。
四、问题生成单:
课题:7.2.2三角形的外角(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.知道什么是三角形的外角,会在简单图形中识别三角形的外角.
2.经历探究外角与它不相邻的两个内角的关系的过程,会证明和运用结论.
3.知道三角形的一个外角大于与它不相邻的任何一个内角.
(二)学习重点和难点:
1.重点:外角的概念,结论的探究和运用.
2.难点:结论的探究和证明.
二、问题导读单:阅读P74—75页回答下列问题:
1.三角形的外角:如图, ∠______就是△ABC的一个外角,也可以说∠____是∠____的外角. 说明此角是如何形成的 _________________________________________
分析说明: ∠ACD是∠ACB的一个_____角,也是∠ACB的一个_____角.故有两角关系为:_____________________________
2.判断图中∠1是不是△ABC的外角:_______________
3.如图,(1)∠1、∠2都是△ABC的外角吗?________________
(2)△ABC共有多少个外角?___________________
请在图中标出△ABC的其它外角.
4.探究题:如图,△ABC中,∠A=70°,∠B=60°,
∠ACD是△ABC的一个外角,
(1)则∠ACB=_____°, ∠ACD=_____°;
(2)∠ACD与∠A、∠B有什么关系?
由此你发现了什么数学结论?
______________________________________________
______________________________________________________________________
5.细心分析研究“P74页探究”回答有关问题.(与同组同学交流)
由探究得到的结论:结论1______________________________________________
结论2______________________________________________________(外角两性质)
三、问题训练单:
6.填空:求出下列各图中∠1的度数.
(1)如图,∠1=______;(2)如图,∠1=______;(3)如图,∠1=______;
(4)如图,∠1=______;(5)如图,∠1=______;(6)如图,∠1=______.
7.判断正误:对的有______,错的有_________.
(1)三角形的一个外角等于两个内角的和.
(2)三角形的一个外角减去它的一个不相邻的内角,等于它的另一个不相邻的内角. (3)三角形的一个外角大于与它不相邻的一个内角.
8.完成下面的证明过程:
如何证明“三角形的一个外角等于与它不相邻的两个内角的和”?
已知:如图,∠ACD是△ABC的一个外角.
求证:∠ACD=∠A+∠B.
证明:因为∠A+∠B+∠C=180°(三角形内角和定理),
所以∠A+∠B=180°-__________.
又因为∠ACD=180°-__________(平角的定义),
所以__________=____________.
四、问题生成单:
课题:7.2.2三角形的外角(2) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
会综合运用内角和定理、外角性质求角度.
(二)学习重点和难点:
1.重点:综合运用内角和定理、外角性质求角度.
2.难点:综合运用内角和定理、外角性质求角度.
二、问题导读单:阅读P74—75页回答下列问题:
1.写出三角形外角的两条性质: __________________________________________
__________________________________________________________________
2. 已知:如图,∠1=30°,∠2=50°,∠3=45°,
则(1)∠4=______°;(2)∠5=______°.
3.已知:如图∠1=40°,∠2=∠3,则
(1)∠4=______°;(2)∠2=______°.
4.如图,AB∥CD,∠B=55°,∠C=40°,则
(1)∠D=______°;(2)∠1=______°.
5. 例2.如图,∠BAE,∠CBF,
∠ACD是△ABC的三个外角,
它们的和是多少?
解:因为∠BAE=∠__+∠____,
∠CBF=∠__+∠___,
∠ACD=__________,
所以∠BAE+∠CBF+∠ACD
=(∠__+∠___)+(________)+(___________)
=2(∠1+_________)=2×180°=360°.
从例2.我们可以得到一个数学结论: 三角形________________________________.
三、问题训练单:
6 已知:如图,∠B=30°,∠C=65°,∠BAD=50°,
求∠CAD的度数.
解:在△ABC中,∠ADC=∠____+∠___=____°+___°=_______.
在△ADC中,∠CAD=180°-_____________
=180°-_____________=_________.
7.已知:如图,在△ABC中,AD是BC边上的高,
∠BAC=80°,∠C=40°,则∠BAD=________°.
8.已知:如图,BD是△ABC的角平分线,
∠A=100°,∠C=30°,则∠ADB=________°.
9.*如图,AD、BE分别是△ABC的高和
角平分线,∠BAC=100°,∠C=30°,则∠1=________°.
10*.△ABC中,∠B=∠A+100,∠C=∠B+200,
求△ABC各内角的度数
11*已知,如图,AB∥CD,AE平分∠BAC,
CE平分∠ACD,求∠E的度数
四、问题生成单:
五、谈本节课收获和体会:
课题:7.3.1多边形(1) 月 日 班级: 姓名:
一、教材分析:∠①②③
(一)学习目标:
1.能说出什么是多边形、n边形、多边形的内角、多边形的外角、多边形的对角线、正多边形.
2.经历探究从n边形的一个顶点出发,可以画出n-3条对角线,它们把n边形分成n-2个三角形的过程,培养合情推理能力.
(二)学习重点和难点:
1.重点:与多边形有关的概念.
2.难点:探究过程.
二、问题导读单:阅读P79—81页回答下列问题:
1.在平面内,由三条线段___________相接组成的图形叫做三角形.由四条线段首尾顺次相接组成的,这种图形应该叫做_______形,类似地,如果一个多边形由___条线段组成,那么这个多边形就叫做______________.填写下图是几边形.
2. 三角形有内角和外角,同样,多边形也有内角和外角.
如五边形ABCDE中内角有______________________
画出∠BAE的两个外角,
3. 多边形的对角线,画出五边形对角线,并写出对角线:
___________________________________
4.凸多边形与不是凸多边形的区别:________________________________________
_______________________________________________________________________
5.正多边形,_______________________的多边形,叫做正多边形.
6.完成P81页练习.
三、问题训练单:
7.判断正误:对的有_______,错的有___________.
(1)∠1是四边形ABCD的外角 (2)∠2是四边形ABCD的外角;
(3)∠3是四边形ABCD的外角; (4)∠4是四边形ABCD的外角;
(5)∠5是四边形ABCD的外角.
8. 画出五边形中∠BAE的一个外角∠1.
这个内角与这个外角有什么关系?
从中得出结论是:
______________________________________
________________________________________
9*.画出下列多边形的全部对角线,并填空:
三角形共有_______条对角线,四边形共有_______条对角线,
五边形共有_______条对角线,
六边形共有_______条对角线.
10*合做探究题
(1)如图,从五边形的同一个顶点出发,
一共可以画2条对角线,这2条对角线
把五边形分成3个三角形;
(2)如图,从六边形的同一个顶点出发,
一共可以画______条对角线,这些对角
线把六边形分成______个三角形;(3)从十边形的同一个顶点出发,一共可以画______条对角线,这些对角线把十边形分成______个三角形;(4)从一百边形的同一个顶点出发,一共可以画______条对角线,这些对角线把一百边形分成______个三角形;(5)从n边形的同一个顶点出发,一共可以画______条对角线,这些对角线把n边形分成______个三角形.
四、问题生成单:
课题:7.3.2多边形的内角和(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.经历探究多边形内角和公式,体会转化思想,体会从特殊到一般的认识问题的方法.
2.会简单运用多边形内角和公式.
(二)学习重点和难点:
1.重点:探究多边形内角和公式.
2.难点:探究多边形内角和时,如何把多边形转化成三角形.
二、问题导读单:阅读P81—83页回答下列问题:
1.细心研读P81页“探究”,三角形的内角和是_______,
正方形、长方形的内角和等于______度(因为___________
______________________________________________),
那任意四边形ABCD的内角和又等于多少 利用左图,连辅助线进行说明.
2.探究题:
(1)如图,从五边形的同一个顶点出发,一共可以画______条对角线,这些对
角线把五边形分成了______个三角形,所以五边形的内角和等于_____×180°.
(2)如图,从六边形的同一个顶点出发,一共可以画_____条对角线,这些对
角线把六边形分成了_____个三角形,所以六边形的内角和等于____×180°.
(3)从n边形的同一个顶点出发,一共可以画________条对角线,这些对角
线把n边形分成了_______个三角形,所以n边形的内角和等于_____×180°.
我们就得出了多边形内角和公式:n边形内角和 =___________________
3. 根据多边形内角和公式填空: 四边形的内角和=_______°,五边形的内角和=_______°,
六边形的内角和=_______°,七边形的内角和=_______°,八边形的内角和=_______°.
4.研读P82页例1,说明在进行本题目的解答过程中应用了的数学原理:____________
_____________________________________________________.完成P83页练习中1题.
三、问题训练单:
5.一个多边形的内角和为720°,那么它是________边形.
6.一个多边形每一个内角等于144°,则其边数是________.
7.下列角度中,不能成为多边形内角和的是( )
A. 600° B. 420° C. 900° D. 1800°
8.如果五边形的三个内角是直角,另两个内角都为n°,则n的值为 ( )
A.105 B.120 C.125 D.135
9.一个四边形的内角中,钝角最多有( ) A.一个 B.两个 C.三个 D.四个
10. 一个四边形四个内角∠A、∠B、∠C、∠D的度数比是2:3:4:3,求这个四边形的四个内角.
分析与简解:我们从∠A、∠B、∠C、∠D的度数比是2:3:4:3,所以如果我们设∠A的度数为2x则∠B、∠C、∠D的度数为___,____,_____.根据题意,列方程:___________________
解得x=30.所以,∠A=2x°=2×____°=_____°.类似,∠B =_______________________、
∠C =____________________________、∠D= _____________________________________
11.四边形ABCD中若∠A +∠B +180° 且: ∠B:∠C:∠D =1:2:3则∠A=___________
12.一个五边形剪去一个角后,剩下的内角和是多少度:________________________________
13.如果一个多边形除了一个内角外,其余各内角这和为1190°,则这个内角为_________度,是一个__________边形.
14.一个多边形截去一个角(不过顶点)后,所形成的一个多边形的内角和是2520°,那么原多边形的边数是 ( ) A.13 B.15 C.17 D.19
四、问题生成单:
课题:7.3.2多边形的内角和(2) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.经历探究多边形外角和的结论,知道多边形外角和等于360°.
2.会运用多边形内角和公式、多边形外角和结论.
(二)学习重点和难点:
1.重点:外角和及运用.
2.难点:探究多边形外角和结论.
二、问题导读单:阅读P81—83页回答下列问题:
1. (1)十二边形的内角和等于________°;
(2)一个多边形的内角和等于2160°,这个多边形是______边形.
2.如图,∠1是△ABC的_______,∠2、∠3也是△ABC的_____.△ABC的外角和∠1+∠2+∠3等于_____度,△ABC的外角和∠1+∠2+∠3等于______°.
3.细心研读P82页例2,回答分析问题,把答案相应写出:
(1)_________________________________________________________________
(2)__________________________________________________________________
(3)_________________________________________________________________
4.思考回答P83页”探究”.______________________________________________
5.得出关于多边形的外角性质结论: ________________________________________
6.图7.3-12中问题,进行实验体会说明的结论是:_____________________________
三、问题训练单:
7.填表:
多边形的边数 3 4 5 6 7 8 12
内角和
外角和
8.填空:如果一个多边形的内角和与外角和相等,那么这个多边形是______边形.
9.填空:如果一个多边形的各外角都等于60°,那么这个多边形是______边形.
10.填空:如果一个多边形的各内角都等于120°,那么这个多边形是______边形.
11.一个多边形的内角和是外角和的2.5倍,它是几边形?
解:设这个多边形为n边形. - - - - 注意学习解题格式
根据题意,列方程得(_______)·180=_______×360.
解得 n=____.
答:这个多边形是_____边形.
12.求下列图中x值
答案:
(1)X=
(2)X=
13.四边形的内角和是_________,外角和是___________
14.一个多边形的每一个外角为18°,则它是一个______边形.
15.当多边形的边数增加1时,其内角和增加______度,外角和增加___度.
16一个正多边形的每个外角都是72°,则这个多边形是__________边形.
17.每个内角都为144°的多边形为______边形.
18.若多边形的内角和等于外角的3倍,则这个多边形的边是______.
19.四边形中,如果有一组对角都是直角,那么另一组对角可能( )
A.都是钝角 B.都是锐角 C.是一个锐角,一个钝角. D. 是一个锐角,一个直角
20**.若一个多边形的各内角都相等,则一个内角与一个外角的度数之比不可能是( ) A.2:1 B.1:1 C.5:2 D.5:4
21**一个多边形的内角中,锐角的个数最多有 ( )
A.3个 B.4个 C.5个 D.6个
22**若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( ) A.90° B.105° C.130° D.120°
四、问题生成单:
五、谈本节课收获和体会:
① ② ③
① ② ③
A
B
C
D
E
F
11题图
9题图
10题图
10题图
11题图
13题图
7题图
6题图
5题图
第6题(2)
第6题(3)
第6题(1)
第6题(4)
第6题(6)
第6题(5)
第3题图
第2题图
第5题图
第4题图
第2题图
________
________
________
________
________
80 °
120 °
75 ° x°
150 °2x°
120 °
x°
