11.2.1 直角三角形中两锐角的关系 第2课时 课件 -人教版八年级数学上册(17张)
文档属性
| 名称 | 11.2.1 直角三角形中两锐角的关系 第2课时 课件 -人教版八年级数学上册(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 380.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-23 22:48:33 | ||
图片预览



文档简介
(共17张PPT)
11.2.1
第2课时
直角三角形的两锐角互余
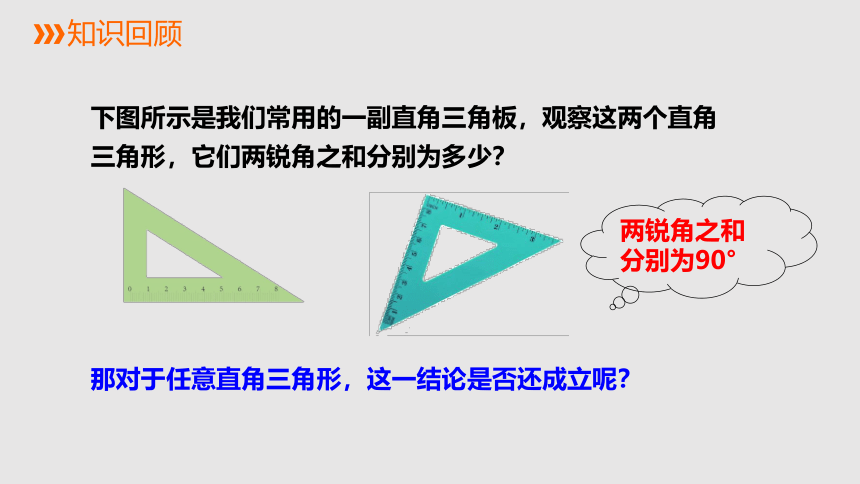
知识回顾
下图所示是我们常用的一副直角三角板,观察这两个直角三角形,它们两锐角之和分别为多少?
那对于任意直角三角形,这一结论是否还成立呢?
两锐角之和分别为90°
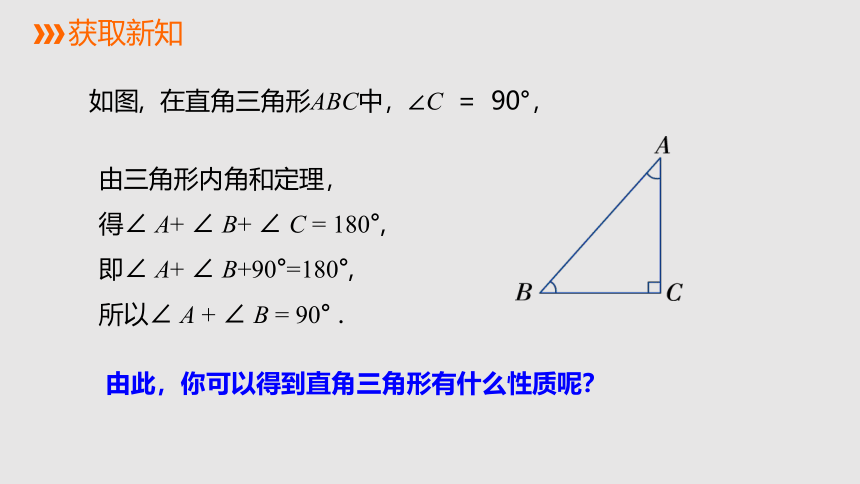
获取新知
由三角形内角和定理,
得∠
A+
∠
B+
∠
C
=
180°,
即∠
A+
∠
B+90°=180°,
所以∠
A
+
∠
B
=
90°
.
由此,你可以得到直角三角形有什么性质呢?
如图,
在直角三角形ABC中,∠C
=
90°,
A
B
C
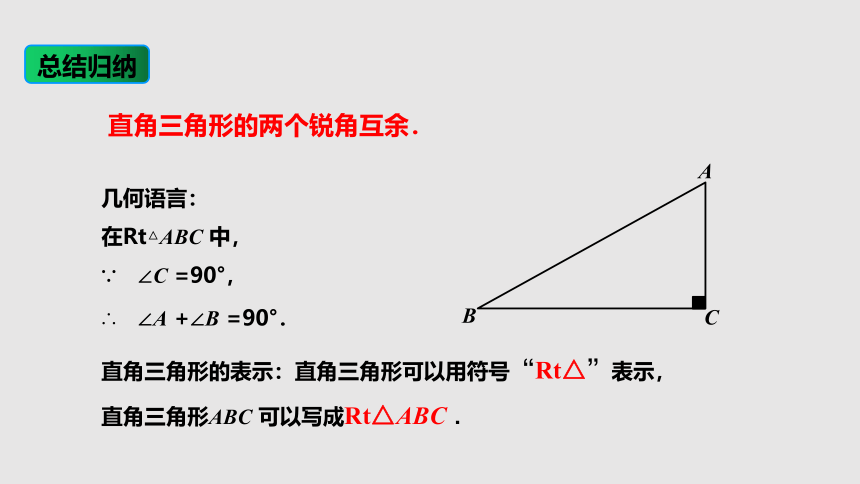
直角三角形的两个锐角互余.
几何语言:
在Rt△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC
可以写成Rt△ABC
.
总结归纳
例题讲解
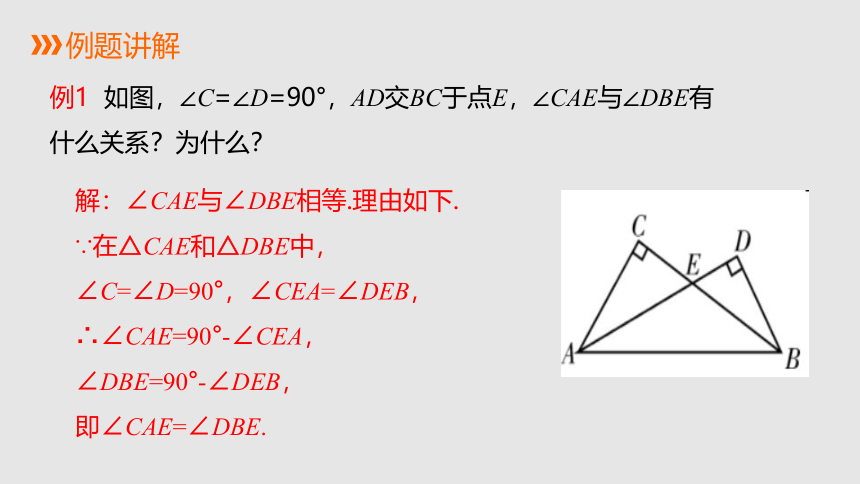
例1
如图,∠C=∠D=90°,AD交BC于点E,∠CAE与∠DBE有什么关系?为什么?
解:∠CAE与∠DBE相等.理由如下.
∵在△CAE和△DBE中,
∠C=∠D=90°,∠CEA=∠DEB,
∴∠CAE=90°-∠CEA,
∠DBE=90°-∠DEB,
即∠CAE=∠DBE.
C
例2
[教材补充例题]如图11-2-5,在△ABC中,CE,BF是两条高.若∠ABF=20°,∠BCE=30°,求∠ACE与∠FBC的度数.
图11-2-5
解:∵在△ABC中,CE,BF是两条高,
∴∠AEC=∠AFB=90°.
∴∠ABF=90°-∠A,∠ACE=90°-∠A.
∴∠ACE=∠ABF=20°.
∵∠BCE=30°,
∴∠BCF=∠BCE+∠ACE=50°.
∵∠BFC=90°,
∴∠FBC=90°-∠BCF=40°.
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,你能得出什么结论?这个结论成立吗?如何验证你的想法?
思考
在△ABC中,
因为
∠A
+∠B
+∠C=180°,
又∠A
+∠B=90°,
所以∠C=90°.
于是△ABC是直角三角形.
证明:
A
B
C
几何语言:
在△ABC
中,
∵ ∠A
+∠B
=90°,
∴ △ABC
是直角三角形.
有两个角互余的三角形是直角三角形.
总结归纳
例题讲解
例3
如图,∠C=90
°,
∠1=
∠2,△ADE是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+
∠A=90
°.
∵
∠1=
∠2,
∴∠1
+
∠A=90
°.
即△ADE是直角三角形.
例4
[教材补充例题]如图11-2-7,AB,ED均垂直于BD,垂足分别是B,D,点C在BD上,且∠ACB=∠CED.求证:△ACE是直角三角形.
图11-2-7
证明:∵AB⊥BD,ED⊥BD,
∴∠ABC=∠CDE=90°.
∴∠CED+∠DCE=90°.
∵∠ACB=∠CED,
∴∠ACB+∠DCE=90°.
又∵∠ACB+∠DCE+∠ACE=180°,
∴∠ACE=90°.
∴△ACE是直角三角形.
判定一个三角形是直角三角形的方法
(1)根据定义:有一个角是直角的三角形是直角三角形;
(2)根据判定方法:有两个角互余的三角形是直角三角形.
总结归纳
随堂演练
1.在Rt△ABC中,∠B是直角,∠C=22°,那么∠A的度数是( )
A.22°
B.58°
C.68°
D.112°
C
2.如图D-5-1,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( )
A.50°
B.60°
C.30°
D.40°
D
图D-5-1
3.在△ABC中,∠A=36°,∠B=54°,那么△ABC是________三角形.
直角
4.
如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是
直角三角形吗?
为什么?
解:△ABD是直角三角形.理由如下:
∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.
课堂小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
谢谢观看!
11.2.1
第2课时
直角三角形的两锐角互余
知识回顾
下图所示是我们常用的一副直角三角板,观察这两个直角三角形,它们两锐角之和分别为多少?
那对于任意直角三角形,这一结论是否还成立呢?
两锐角之和分别为90°
获取新知
由三角形内角和定理,
得∠
A+
∠
B+
∠
C
=
180°,
即∠
A+
∠
B+90°=180°,
所以∠
A
+
∠
B
=
90°
.
由此,你可以得到直角三角形有什么性质呢?
如图,
在直角三角形ABC中,∠C
=
90°,
A
B
C
直角三角形的两个锐角互余.
几何语言:
在Rt△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC
可以写成Rt△ABC
.
总结归纳
例题讲解
例1
如图,∠C=∠D=90°,AD交BC于点E,∠CAE与∠DBE有什么关系?为什么?
解:∠CAE与∠DBE相等.理由如下.
∵在△CAE和△DBE中,
∠C=∠D=90°,∠CEA=∠DEB,
∴∠CAE=90°-∠CEA,
∠DBE=90°-∠DEB,
即∠CAE=∠DBE.
C
例2
[教材补充例题]如图11-2-5,在△ABC中,CE,BF是两条高.若∠ABF=20°,∠BCE=30°,求∠ACE与∠FBC的度数.
图11-2-5
解:∵在△ABC中,CE,BF是两条高,
∴∠AEC=∠AFB=90°.
∴∠ABF=90°-∠A,∠ACE=90°-∠A.
∴∠ACE=∠ABF=20°.
∵∠BCE=30°,
∴∠BCF=∠BCE+∠ACE=50°.
∵∠BFC=90°,
∴∠FBC=90°-∠BCF=40°.
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,你能得出什么结论?这个结论成立吗?如何验证你的想法?
思考
在△ABC中,
因为
∠A
+∠B
+∠C=180°,
又∠A
+∠B=90°,
所以∠C=90°.
于是△ABC是直角三角形.
证明:
A
B
C
几何语言:
在△ABC
中,
∵ ∠A
+∠B
=90°,
∴ △ABC
是直角三角形.
有两个角互余的三角形是直角三角形.
总结归纳
例题讲解
例3
如图,∠C=90
°,
∠1=
∠2,△ADE是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+
∠A=90
°.
∵
∠1=
∠2,
∴∠1
+
∠A=90
°.
即△ADE是直角三角形.
例4
[教材补充例题]如图11-2-7,AB,ED均垂直于BD,垂足分别是B,D,点C在BD上,且∠ACB=∠CED.求证:△ACE是直角三角形.
图11-2-7
证明:∵AB⊥BD,ED⊥BD,
∴∠ABC=∠CDE=90°.
∴∠CED+∠DCE=90°.
∵∠ACB=∠CED,
∴∠ACB+∠DCE=90°.
又∵∠ACB+∠DCE+∠ACE=180°,
∴∠ACE=90°.
∴△ACE是直角三角形.
判定一个三角形是直角三角形的方法
(1)根据定义:有一个角是直角的三角形是直角三角形;
(2)根据判定方法:有两个角互余的三角形是直角三角形.
总结归纳
随堂演练
1.在Rt△ABC中,∠B是直角,∠C=22°,那么∠A的度数是( )
A.22°
B.58°
C.68°
D.112°
C
2.如图D-5-1,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( )
A.50°
B.60°
C.30°
D.40°
D
图D-5-1
3.在△ABC中,∠A=36°,∠B=54°,那么△ABC是________三角形.
直角
4.
如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是
直角三角形吗?
为什么?
解:△ABD是直角三角形.理由如下:
∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.
课堂小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
谢谢观看!
