1.2 展开与折叠 课件(共24张PPT)
文档属性
| 名称 | 1.2 展开与折叠 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-25 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第一章
丰富的图形世界
2
展开与折叠
知识点一
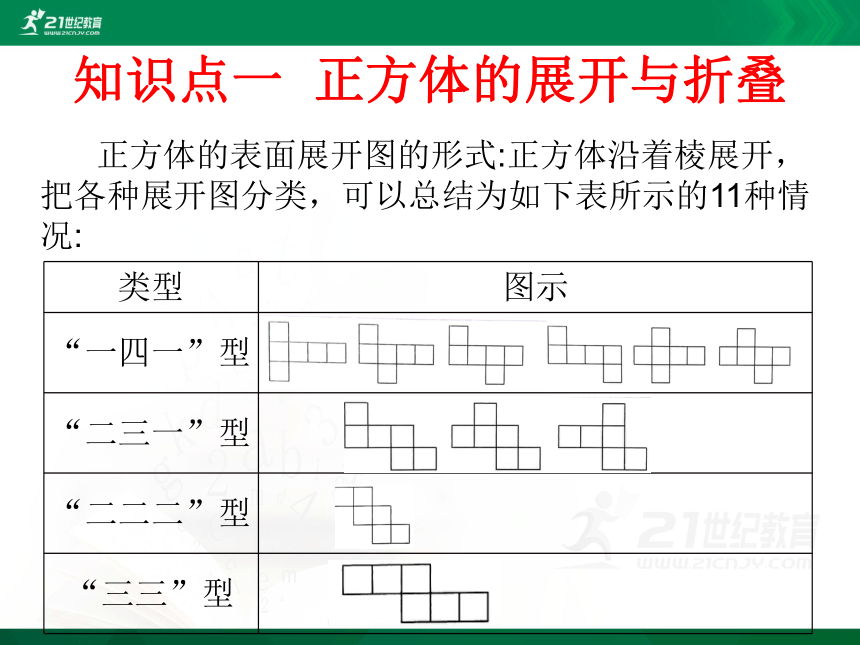
正方体的展开与折叠
正方体的表面展开图的形式:正方体沿着棱展开,把各种展开图分类,可以总结为如下表所示的11种情况:
类型
图示
“一四一”型
“二三一”型
“二二二”型
“三三”型
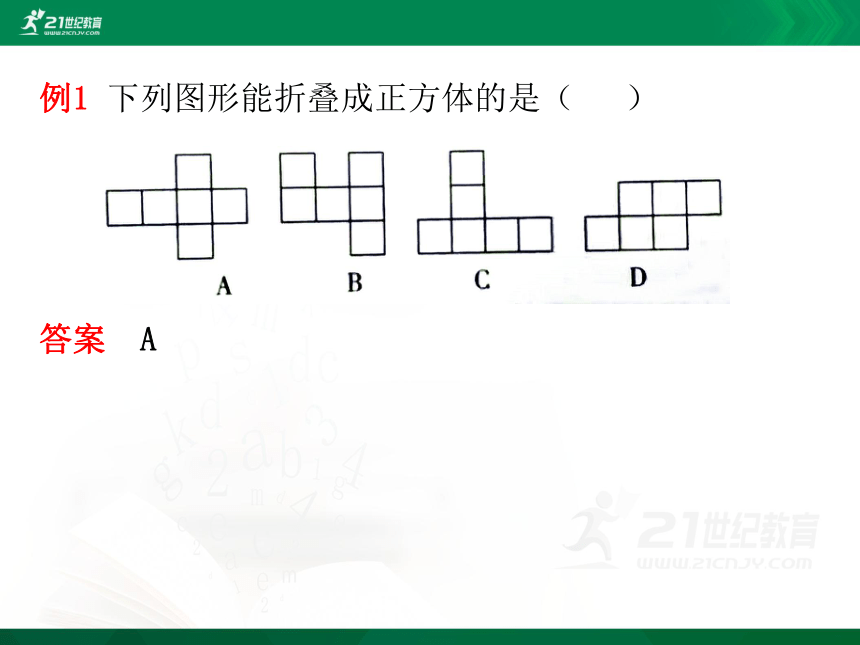
例1
下列图形能折叠成正方体的是(
)
例1
下列图形能折叠成正方体的是(
)
答案
A
例1
下列图形能折叠成正方体的是(
)
答案
A
解析
A.能折叠成正方体,故此选项符合题意;B.出现了“凹”字格,不能折叠成正方体,故此选项不符合题意;C.折叠后有两个面重合,不能折叠成正方体,故此选项不符合题意;D.出现了“田”字格,不能折叠成正方体,故此选项不符合题意故选A.
方法技巧
正方体的表面展开图由六个正方形组成,它的展开图不能是下列两种情况:
(1)一线不过四:在正方体的表面展开图中,一条直线上的小正方形不会超过四个,下图就不是正方体的表面展开图.
(2)“田”“凹”“L”应弃之:在正方体的表面展开图中不会有“田”“凹”“L”字形.如图所示.
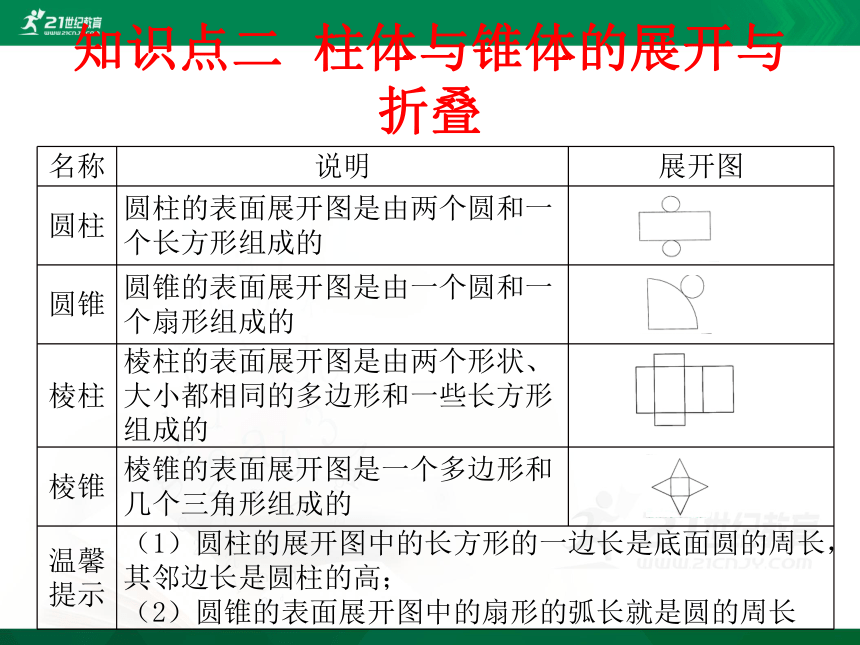
知识点二
柱体与锥体的展开与折叠
名称
说明
展开图
圆柱
圆柱的表面展开图是由两个圆和一个长方形组成的
圆锥
圆锥的表面展开图是由一个圆和一个扇形组成的
棱柱
棱柱的表面展开图是由两个形状、大小都相同的多边形和一些长方形组成的
棱锥
棱锥的表面展开图是一个多边形和几个三角形组成的
温馨提示
(1)圆柱的展开图中的长方形的一边长是底面圆的周长,其邻边长是圆柱的高;
(2)圆锥的表面展开图中的扇形的弧长就是圆的周长
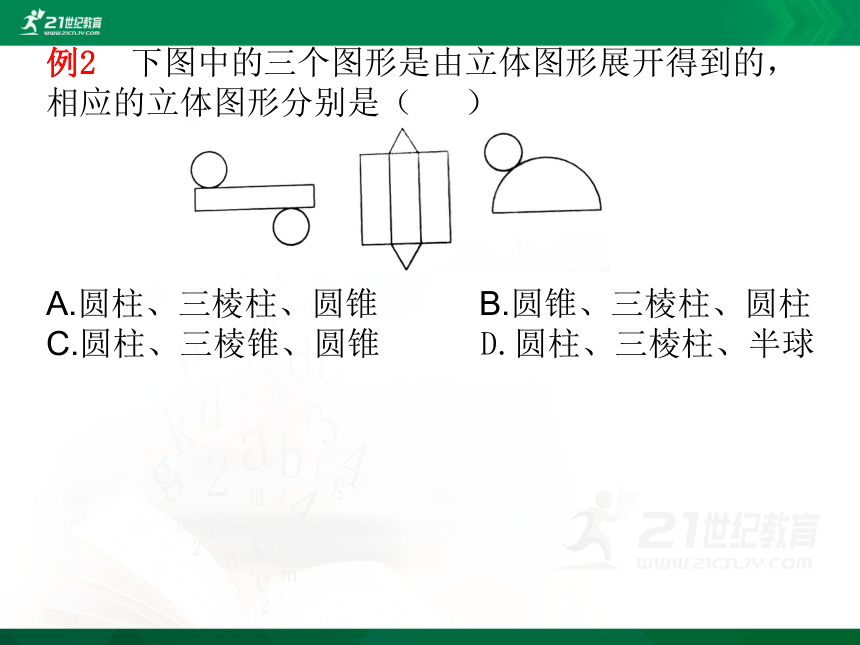
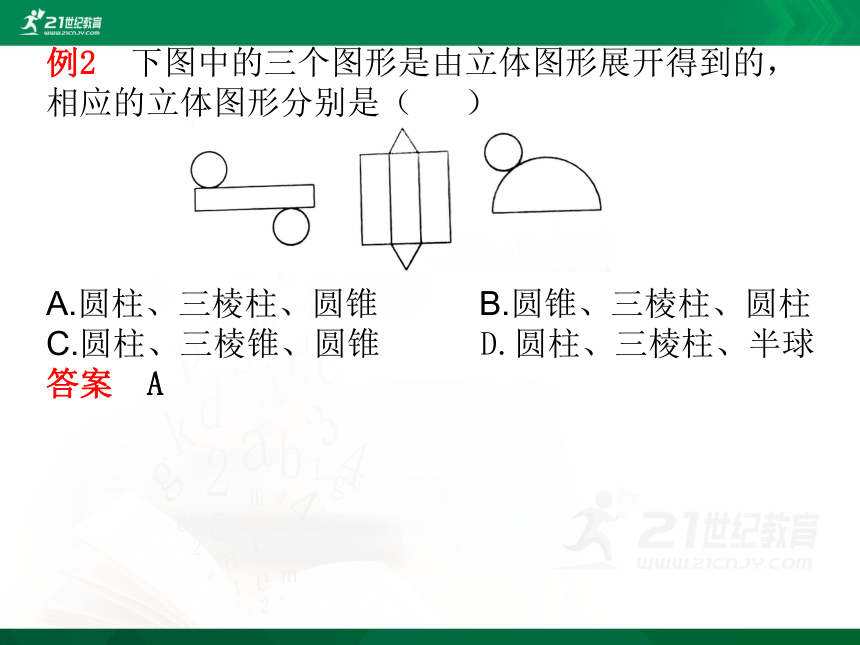
例2
下图中的三个图形是由立体图形展开得到的,相应的立体图形分别是(
)
A.圆柱、三棱柱、圆锥
B.圆锥、三棱柱、圆柱
C.圆柱、三棱锥、圆锥
D.圆柱、三棱柱、半球
例2
下图中的三个图形是由立体图形展开得到的,相应的立体图形分别是(
)
A.圆柱、三棱柱、圆锥
B.圆锥、三棱柱、圆柱
C.圆柱、三棱锥、圆锥
D.圆柱、三棱柱、半球
答案
A
例2
下图中的三个图形是由立体图形展开得到的,相应的立体图形分别是(
)
A.圆柱、三棱柱、圆锥
B.圆锥、三棱柱、圆柱
C.圆柱、三棱锥、圆锥
D.圆柱、三棱柱、半球
答案
A
解析
第一个图形,上、下是两个相同的圆,中间是一个长方形,所以它是圆柱的表面展开图;第二个图形,上、下是两个完全相同的三角形,中间是三个长方形,所以它是三棱柱的表面展开图;第三个图形由一个圆和一个半圆(扇形)组成,所以它是圆锥的表面展开图.
经典例题
题型一
由表面展开图到几何体
例1
下图是一个正方体的展开图,六个面分别标有汉字,那么和“图”字相对的字是__________.
题型一
由表面展开图到几何体
例1
下图是一个正方体的展开图,六个面分别标有汉字,那么和“图”字相对的字是__________.
答案
本
题型一
由表面展开图到几何体
例1
下图是一个正方体的展开图,六个面分别标有汉字,那么和“图”字相对的字是__________.
答案
本
解析
正方体的表面展开图,相对的面之间一定相隔一个正方形,和“基”字相对的字是“何”;和“本”字相对的字是“图”;和“几”字相对的字是“形”.
题型一
由表面展开图到几何体
方法归纳
解决此类问题的方法一般有两种:一是根据相对面的分布规律进行判断,相对面绝对不相邻(无公共边且无公共点);同一层有三个或四个面时,相间的两个面一定是相对面;二是通过动手折叠或展开正方体确定正确结果.
题型二
由几何体到表面展开图
例2
下图是正方体纸盒,展开后可以得到(
)
题型二
由几何体到表面展开图
例2
下图是正方体纸盒,展开后可以得到(
)
答案
A
题型二
由几何体到表面展开图
例2
下图是正方体纸盒,展开后可以得到(
)
答案
A
解析
根据折叠后白色圆与蓝色圆所在面的位置进行判断即可.
题型二
由几何体到表面展开图
例2
下图是正方体纸盒,展开后可以得到(
)
答案
A
解析
根据折叠后白色圆与蓝色圆所在面的位置进行判断即可.
点拨
解决此类问题,要充分考虑带有各种符号的面的特点及位置.
易错易混
易错点
将表面展开图还原成几何体时会漏情况
将一个表面展开图还原成几何体,一般有两种形式向外折和向里折,稍不留心就容易漏掉一种.
例题
下图是一个长方体的表面展开图,每个面都标注了字母,如果F在前面,从左面看到的是B,那么哪一个面会在上面?
例题
下图是一个长方体的表面展开图,每个面都标注了字母,如果F在前面,从左面看到的是B,那么哪一个面会在上面?
解析
面E或面C会在上面.
例题
下图是一个长方体的表面展开图,每个面都标注了字母,如果F在前面,从左面看到的是B,那么哪一个面会在上面?
解析
面E或面C会在上面.
易错警示
解此题时,易忽略向里折和向外折两种折法中的一种.
第一章
丰富的图形世界
2
展开与折叠
知识点一
正方体的展开与折叠
正方体的表面展开图的形式:正方体沿着棱展开,把各种展开图分类,可以总结为如下表所示的11种情况:
类型
图示
“一四一”型
“二三一”型
“二二二”型
“三三”型
例1
下列图形能折叠成正方体的是(
)
例1
下列图形能折叠成正方体的是(
)
答案
A
例1
下列图形能折叠成正方体的是(
)
答案
A
解析
A.能折叠成正方体,故此选项符合题意;B.出现了“凹”字格,不能折叠成正方体,故此选项不符合题意;C.折叠后有两个面重合,不能折叠成正方体,故此选项不符合题意;D.出现了“田”字格,不能折叠成正方体,故此选项不符合题意故选A.
方法技巧
正方体的表面展开图由六个正方形组成,它的展开图不能是下列两种情况:
(1)一线不过四:在正方体的表面展开图中,一条直线上的小正方形不会超过四个,下图就不是正方体的表面展开图.
(2)“田”“凹”“L”应弃之:在正方体的表面展开图中不会有“田”“凹”“L”字形.如图所示.
知识点二
柱体与锥体的展开与折叠
名称
说明
展开图
圆柱
圆柱的表面展开图是由两个圆和一个长方形组成的
圆锥
圆锥的表面展开图是由一个圆和一个扇形组成的
棱柱
棱柱的表面展开图是由两个形状、大小都相同的多边形和一些长方形组成的
棱锥
棱锥的表面展开图是一个多边形和几个三角形组成的
温馨提示
(1)圆柱的展开图中的长方形的一边长是底面圆的周长,其邻边长是圆柱的高;
(2)圆锥的表面展开图中的扇形的弧长就是圆的周长
例2
下图中的三个图形是由立体图形展开得到的,相应的立体图形分别是(
)
A.圆柱、三棱柱、圆锥
B.圆锥、三棱柱、圆柱
C.圆柱、三棱锥、圆锥
D.圆柱、三棱柱、半球
例2
下图中的三个图形是由立体图形展开得到的,相应的立体图形分别是(
)
A.圆柱、三棱柱、圆锥
B.圆锥、三棱柱、圆柱
C.圆柱、三棱锥、圆锥
D.圆柱、三棱柱、半球
答案
A
例2
下图中的三个图形是由立体图形展开得到的,相应的立体图形分别是(
)
A.圆柱、三棱柱、圆锥
B.圆锥、三棱柱、圆柱
C.圆柱、三棱锥、圆锥
D.圆柱、三棱柱、半球
答案
A
解析
第一个图形,上、下是两个相同的圆,中间是一个长方形,所以它是圆柱的表面展开图;第二个图形,上、下是两个完全相同的三角形,中间是三个长方形,所以它是三棱柱的表面展开图;第三个图形由一个圆和一个半圆(扇形)组成,所以它是圆锥的表面展开图.
经典例题
题型一
由表面展开图到几何体
例1
下图是一个正方体的展开图,六个面分别标有汉字,那么和“图”字相对的字是__________.
题型一
由表面展开图到几何体
例1
下图是一个正方体的展开图,六个面分别标有汉字,那么和“图”字相对的字是__________.
答案
本
题型一
由表面展开图到几何体
例1
下图是一个正方体的展开图,六个面分别标有汉字,那么和“图”字相对的字是__________.
答案
本
解析
正方体的表面展开图,相对的面之间一定相隔一个正方形,和“基”字相对的字是“何”;和“本”字相对的字是“图”;和“几”字相对的字是“形”.
题型一
由表面展开图到几何体
方法归纳
解决此类问题的方法一般有两种:一是根据相对面的分布规律进行判断,相对面绝对不相邻(无公共边且无公共点);同一层有三个或四个面时,相间的两个面一定是相对面;二是通过动手折叠或展开正方体确定正确结果.
题型二
由几何体到表面展开图
例2
下图是正方体纸盒,展开后可以得到(
)
题型二
由几何体到表面展开图
例2
下图是正方体纸盒,展开后可以得到(
)
答案
A
题型二
由几何体到表面展开图
例2
下图是正方体纸盒,展开后可以得到(
)
答案
A
解析
根据折叠后白色圆与蓝色圆所在面的位置进行判断即可.
题型二
由几何体到表面展开图
例2
下图是正方体纸盒,展开后可以得到(
)
答案
A
解析
根据折叠后白色圆与蓝色圆所在面的位置进行判断即可.
点拨
解决此类问题,要充分考虑带有各种符号的面的特点及位置.
易错易混
易错点
将表面展开图还原成几何体时会漏情况
将一个表面展开图还原成几何体,一般有两种形式向外折和向里折,稍不留心就容易漏掉一种.
例题
下图是一个长方体的表面展开图,每个面都标注了字母,如果F在前面,从左面看到的是B,那么哪一个面会在上面?
例题
下图是一个长方体的表面展开图,每个面都标注了字母,如果F在前面,从左面看到的是B,那么哪一个面会在上面?
解析
面E或面C会在上面.
例题
下图是一个长方体的表面展开图,每个面都标注了字母,如果F在前面,从左面看到的是B,那么哪一个面会在上面?
解析
面E或面C会在上面.
易错警示
解此题时,易忽略向里折和向外折两种折法中的一种.
