沪粤版九年级上册物理 第14章 探究欧姆定律 达标测试卷(含答案)
文档属性
| 名称 | 沪粤版九年级上册物理 第14章 探究欧姆定律 达标测试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 191.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-24 15:46:18 | ||
图片预览



文档简介
第十四章达标测试卷
一、填空题(每空2分,共20分)
1.有阻值相同的三个电阻,以任意方式连接,得到电阻的最大阻值与最小阻值之比是________。
2.如图所示,电路中电源电压恒定,定值电阻R1=20 Ω,只闭合开关S1,电流表示数为0.3 A;同时闭合开关S1、S2,电流表示数为0.5 A,则R2的阻值为________Ω。
(第2题) (第3题) (第4题) (第5题)
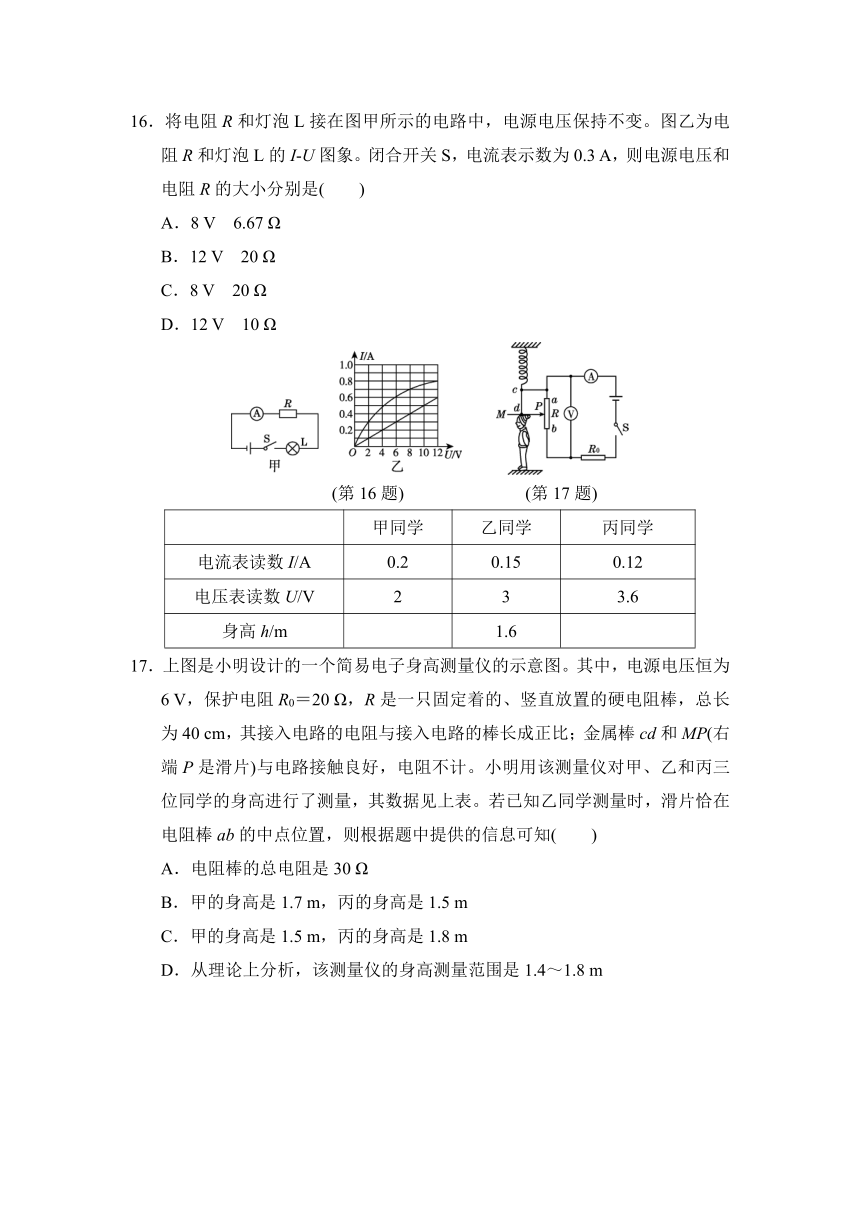
3.如图所示,已知电源电压恒定,且定值电阻R1的阻值大小已知,闭合开关,当将电压表接在a、b时其示数为U1,当将电压表接在b、c时其示数为U2,则可求出未知电阻的阻值Rx=________。
4.如图所示,电源电压保持不变,R1的阻值为15 Ω,当开关S断开时,电流表示数为0.4 A,当开关S闭合时,电流表示数为0.6 A,则R2=________Ω。
5.【新题】在某市中小学生创客比赛中,晓光设计了一个暖箱温度显示器,如图甲所示,其原理是利用电压表的示数表示暖箱内的温度,已知电源电压恒定为4 V,R0的阻值为150 Ω,R1是热敏电阻,图乙是它的阻值—温度的关系图象,电压表的量程为0~3 V,则暖箱内的最高温度是________℃。
6.如图所示,三个阻值均为10 Ω的电阻串联接在电压为U的电路中,用一只电流表接在R2两端时,示数为1.5 A,若改用一只电压表替换电流表,则电压表的示数为________V。
(第6题) (第7题) (第8题) (第9题) (第10题)
7.如图所示,电源电压保持3 V不变,小灯泡L上标有“2.5 V 0.2 A”字样,小灯泡的阻值保持不变,开关S1闭合,S2断开时,灯泡正常发光,则R0的电阻值是________Ω。
8.如图所示,滑动变阻器R2的最大阻值与定值电阻R1相等。闭合开关S,当滑片P在a端时,此时电流表示数为I1;当滑片P在b端时,电流表示数为I2,则I1∶I2=________。
9.如图所示的电路中,电源电压为13.5 V,闭合开关,调节滑动变阻器滑片P从最右端b移动到最左端a,电流表示数由0.18 A变为0.54 A,则滑片位于b点时电压表示数为________V。
10.如图所示,电源电压不变。闭合开关S,移动滑动变阻器的滑片P至某一位置时,电流表的示数为I1;移动滑片P至另一位置时,电流表的示数为I2,电压表示数为1 V。若I1:I2=4:3,前后两次滑动变阻器的阻值之比为2:3,则电源电压为________V。
二、选择题(每题2分,共14分)
11.【新题】小明测量不同型号铅笔在纸上涂画所得线条的电阻,实验步骤如下:
(1)用铅笔在纸上画出两段长为15 cm的线条,在其中一段线条上重复涂画3次,另一段6次;
(2)换用不同型号铅笔重复(1)的操作,得到多组等长等宽的线条(如图);
(3)测出每段线条两端的电阻记录在表中。
根据实验数据,可推测电阻最小的是( )
A.① B.② C.③ D.④
12.如图所示,电源电压保持不变,电阻R1:R2=3:4。S闭合时,甲、乙两处接入电压表;S断开时,甲、乙两处接入电流表。则S闭合时甲、乙两处电压表示数之比U甲:U乙与S断开时甲、乙两处电流表示数之比I甲:I乙分别是( )
A.3:4,1:1 B.3:4,3:4 C.3:4,4:3 D.1:4,4:3
(第12题) (第13题)
13.如图所示的钨丝是将一个白炽灯去除玻璃罩制成的,闭合开关S,小灯泡L发光,钨丝不发光,向钨丝吹气时,小灯泡L变亮,用酒精灯给钨丝加热,小灯泡L逐渐变暗直至熄灭,由实验可知( )
A.钨丝的电阻随温度升高而减小
B.向钨丝吹气时,钨丝电阻变小
C.给钨丝加热时,电路中的电流变大
D.小灯泡L发光而钨丝不发光是因为通过钨丝的电流小于小灯泡L的电流
14.某同学在没有电流表的情况下(电源电压未知但不变),利用电压表和已知阻值的定值电阻R0,测量未知电阻Rx阻值,图中不能实现测量Rx阻值的电路图是( )
A B C D
15.如图甲所示,电源电压不变,R2为电阻箱,调节R2时电流表示数I随之变化。如图乙所示的是电阻箱阻值R2与电流表示数的倒数的图象。则定值电阻R1与电源电压U的大小分别为( )
A.5 Ω 30 V
B.5 Ω 2.5 V
C.10 Ω 20 V
D.10 Ω 10 V
16.将电阻R和灯泡L接在图甲所示的电路中,电源电压保持不变。图乙为电阻R和灯泡L的I?U图象。闭合开关S,电流表示数为0.3 A,则电源电压和电阻R的大小分别是( )
A.8 V 6.67 Ω
B.12 V 20 Ω
C.8 V 20 Ω
D.12 V 10 Ω
(第16题) (第17题)
甲同学 乙同学 丙同学
电流表读数I/A 0.2 0.15 0.12
电压表读数U/V 2 3 3.6
身高h/m
1.6
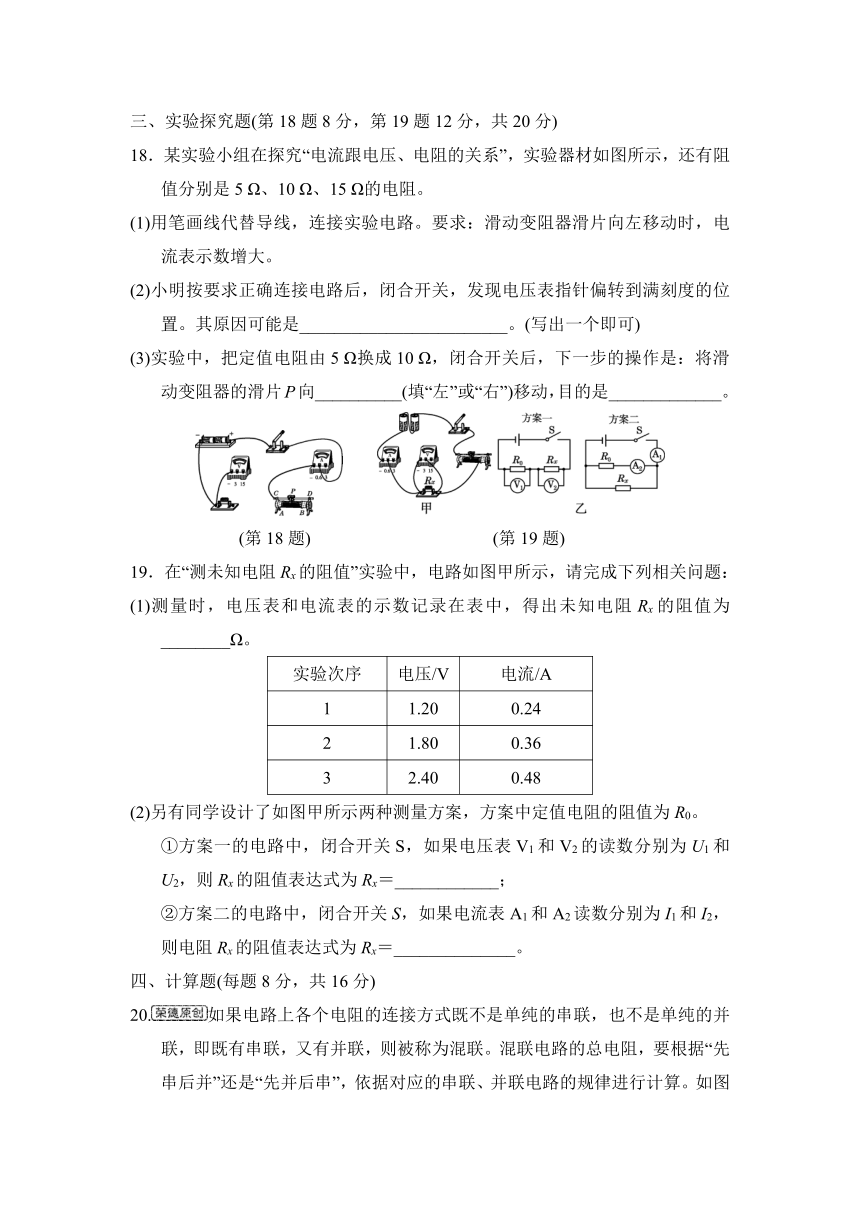
17.上图是小明设计的一个简易电子身高测量仪的示意图。其中,电源电压恒为6 V,保护电阻R0=20 Ω,R是一只固定着的、竖直放置的硬电阻棒,总长为40 cm,其接入电路的电阻与接入电路的棒长成正比;金属棒cd和MP(右端P是滑片)与电路接触良好,电阻不计。小明用该测量仪对甲、乙和丙三位同学的身高进行了测量,其数据见上表。若已知乙同学测量时,滑片恰在电阻棒ab的中点位置,则根据题中提供的信息可知( )
A.电阻棒的总电阻是30 Ω
B.甲的身高是1.7 m,丙的身高是1.5 m
C.甲的身高是1.5 m,丙的身高是1.8 m
D.从理论上分析,该测量仪的身高测量范围是1.4~1.8 m
三、实验探究题(第18题8分,第19题12分,共20分)
18.某实验小组在探究“电流跟电压、电阻的关系”,实验器材如图所示,还有阻值分别是5 Ω、10 Ω、15 Ω的电阻。
(1)用笔画线代替导线,连接实验电路。要求:滑动变阻器滑片向左移动时,电流表示数增大。
(2)小明按要求正确连接电路后,闭合开关,发现电压表指针偏转到满刻度的位置。其原因可能是________________________。(写出一个即可)
(3)实验中,把定值电阻由5 Ω换成10 Ω,闭合开关后,下一步的操作是:将滑动变阻器的滑片P向__________(填“左”或“右”)移动,目的是_____________。
(第18题) (第19题)
19.在“测未知电阻Rx的阻值”实验中,电路如图甲所示,请完成下列相关问题:
(1)测量时,电压表和电流表的示数记录在表中,得出未知电阻Rx的阻值为________Ω。
实验次序 电压/V 电流/A
1 1.20 0.24
2 1.80 0.36
3 2.40 0.48
(2)另有同学设计了如图甲所示两种测量方案,方案中定值电阻的阻值为R0。
①方案一的电路中,闭合开关S,如果电压表V1和V2的读数分别为U1和U2,则Rx的阻值表达式为Rx=____________;
②方案二的电路中,闭合开关S,如果电流表A1和A2读数分别为I1和I2,则电阻Rx的阻值表达式为Rx=______________。
四、计算题(每题8分,共16分)
20.如果电路上各个电阻的连接方式既不是单纯的串联,也不是单纯的并联,即既有串联,又有并联,则被称为混联。混联电路的总电阻,要根据“先串后并”还是“先并后串”,依据对应的串联、并联电路的规律进行计算。如图所示的混联电路中,电源电压等于6 V,R1=10 Ω,R2=20 Ω,R3=30 Ω,则:
(1)电路中的总电阻为多少?
(2)电流表的示数为多少?
(3)电压表的示数为多少?
21.在实际电路中电流表、电压表的内阻不能忽略。某同学用伏安法测量一个未知电阻Rx,他先将电压表、电流表按图甲所示的方法连接在电源电压恒定的电路中,测得电压表、电流表的示数分别为3.0 V、3.0 mA。接着在同一电路中,他又将同一电压表、电流表按图乙所示的方法连接,测得电压表、电流表的示数分别为2.9 V、4.0 mA。
(1)求出电流表的内阻RA。
(2)求出待测电阻Rx的真实值。
(3)如果电流表的内阻忽略不计,且电压表的内阻不是无限大的。请分析说明题中利用哪种接法测量电阻Rx更准确。
答案
一、1.9∶1 2.30 3. 4.7.5 5.100
6.10 点拨:当电流表并联在R2两端时,R2被短路,R1、R3串联,电流表测电路中的电流,根据欧姆定律可得,电压U=I(R1+R3)=1.5 A×(10 Ω+10 Ω)=30 V;当电流表换成了电压表时,三电阻串联,电压表测R2两端的电压,此时电路中的电流:I′===1 A,电压表的示数:U2=I′R2=1 A×10 Ω=10 V。
7.2.5 点拨:开关S1闭合、S2断开时,灯泡与R0串联,电流表测量电路电流,因为灯泡正常发光,所以电路电流为0.2 A,由I=可得,R总===15 Ω,RL===12.5 Ω,又因为串联电路的总电阻等于各部分电阻之和,所以R0的阻值:R0=R总-RL=15 Ω-12.5 Ω=2.5 Ω。
8.1∶1 9.9
10.4 点拨:由图知,R与变阻器串联,电压表测R两端电压,电流表测电路中电流,若前后两次滑动变阻器的阻值分别为R1、R2,则:=,即:R1=R2,根据串联电路特点和欧姆定律有:I1=,I2=,则:===,化简可得:=。当移动滑片P至另一位置时,电流表的示数为I2,电压表示数为1 V,即:UR=1 V,串联电路中电流处处相等,由欧姆定律知:=,所以U2=×UR=3UR=3×1 V=3 V,所以电源电压:U=U2+UR=3 V+1 V=4 V。
二、11.D 12.B 13.B 14.D
15.B 点拨:由电路图可知,R1与R2串联,电流表测电路中的电流,由图乙可知,当R2=0 Ω时,电路中的电流I1=0.5 A,此时只有R1接入电路,则由I=可得,电源电压U=I1R1=0.5 A×R1;当R2=10 Ω时,电路中的电流I2= A,此时电源电压U=I2(R1+R2)= A×(R1+10 Ω);因电源电压不变,所以0.5 A×R1= A×(R1+10 Ω),解得,R1=5 Ω,电源电压U=I1R1=0.5 A×5 Ω=2.5 V。
16.C
17.D 点拨:由电路图可知,滑动变阻器R与定值电阻R0串联,电流表测电路中的电流,电压表测R两端的电压。乙同学测量时,滑片恰在电阻棒ab的中点位置,由I=可得,此时电阻棒的电阻为R===20 Ω,则电阻棒的总电阻R=40 Ω,故A错误;已知总长为40 cm,所以1 cm的电阻为1 Ω,甲同学量身高时接入电路的电阻为R1===10 Ω,接入电路的长度为h1==10 cm=0.1 m,所以甲同学的身高是1.6 m-0.2 m+0.1 m=1.5 m,丙同学量身高时接入电路的电阻为R2===30 Ω,接入电路的长度为h2==30 cm=0.3 m,所以丙同学的身高是1.6 m-0.2 m+0.3 m=1.7 m,故B、C错误;当滑片在a点时,滑动变阻器全部接入电路,所以测量范围最大是1.6 m-0.2 m+0.4 m=1.8 m,当滑片在b点时,滑动变阻器接入电路电阻为0,所以测量范围最小是1.6 m-0.2 m=1.4 m,则从理论上分析,该测量仪的身高测量范围是1.4~1.8 m,故D正确。
三、18.解:(1)如图所示。
(2)定值电阻断路(合理即可)
(3)右;控制定值电阻两端的电压不变
19.(1)5 (2)①R0 ②
点拨:(1)由表中数据,根据欧姆定律得,R1===5 Ω,同理,R2=5 Ω,R3=5 Ω,故三次测量电阻值的平均值为5 Ω,未知电阻Rx的阻值为5 Ω。
(2)①方案一的电路中,闭合开关S,两电阻串联,电压表V1测R0的电压,电压表V2测未知电阻的电压,如果电压表V1和V2的读数分别为U1和U2,则有=,故Rx的阻值表达式为Rx=R0。
②方案二的电路中,闭合开关S,两电阻并联,A2测定值电阻的电流,A1测干路电流:
由欧姆定律得,电源电压:U=I2R0,
根据并联电路电流的规律,通过待测电阻的电流为Ix=I1-I2,
由欧姆定律得,未知电阻Rx的阻值表达式为Rx==。
四、20.解:(1)R1和R2串联后总电阻R′=R1+R2=10 Ω+20 Ω=30 Ω,R′与R3并联,电路中总电阻为R,=+=+=,得R=15 Ω。
(2)电流表测干路电流,示数为I===0.4 A。
(3)R1和R2串联,该支路两端电压等于电源电压,该支路电流I′===0.2 A,电压表测量R2两端电压;示数为U2=I′R2=0.2 A×20 Ω=4 V。
21.解:(1)图甲中,电压表测量电源电压,电流表测通过电阻Rx的电流,因为图甲中电压表的示数为3.0 V,所以电源电压U=3.0 V,即UA+Ux=3.0 V,图乙中,电压表测量电阻Rx两端的电压,电流表测量通过电阻Rx和电压表的总电流,图乙中电压表的示数为2.9 V,即Ux=2.9 V,所以电流表分得的电压:UA=U-Ux=3.0 V-2.9 V=0.1 V,而IA=4.0 mA,电流表的内阻:RA===25 Ω。
(2)电源电压U=3.0 V,图甲中电流I=3.0 mA,电流表与Rx的总电阻:R===1 000 Ω,即RA+Rx=1 000 Ω,则待测电阻Rx的真实值:Rx=1 000 Ω-RA=1 000 Ω-25 Ω=975 Ω。
(3)在图甲中,如果电流表的内阻忽略不计(即电流表的内阻为零),根据串联电路的分压规律可知,电流表分得的电压为零,电压表测量Rx两端的电压,电流表测量通过Rx的电流,则测得的电阻值准确。
在图乙中,如果电压表的内阻不是无限大的,根据并联电路的分流规律可知,电压表要分得一部分电流,则电流表测得的电流偏大,电压表测量Rx两端的电压,根据R=知,测得的电阻值偏小。
综上所述,如果电流表的内阻忽略不计,且电压表的内阻不是无限大的,利用图甲的测量方法更准确。
一、填空题(每空2分,共20分)
1.有阻值相同的三个电阻,以任意方式连接,得到电阻的最大阻值与最小阻值之比是________。
2.如图所示,电路中电源电压恒定,定值电阻R1=20 Ω,只闭合开关S1,电流表示数为0.3 A;同时闭合开关S1、S2,电流表示数为0.5 A,则R2的阻值为________Ω。
(第2题) (第3题) (第4题) (第5题)
3.如图所示,已知电源电压恒定,且定值电阻R1的阻值大小已知,闭合开关,当将电压表接在a、b时其示数为U1,当将电压表接在b、c时其示数为U2,则可求出未知电阻的阻值Rx=________。
4.如图所示,电源电压保持不变,R1的阻值为15 Ω,当开关S断开时,电流表示数为0.4 A,当开关S闭合时,电流表示数为0.6 A,则R2=________Ω。
5.【新题】在某市中小学生创客比赛中,晓光设计了一个暖箱温度显示器,如图甲所示,其原理是利用电压表的示数表示暖箱内的温度,已知电源电压恒定为4 V,R0的阻值为150 Ω,R1是热敏电阻,图乙是它的阻值—温度的关系图象,电压表的量程为0~3 V,则暖箱内的最高温度是________℃。
6.如图所示,三个阻值均为10 Ω的电阻串联接在电压为U的电路中,用一只电流表接在R2两端时,示数为1.5 A,若改用一只电压表替换电流表,则电压表的示数为________V。
(第6题) (第7题) (第8题) (第9题) (第10题)
7.如图所示,电源电压保持3 V不变,小灯泡L上标有“2.5 V 0.2 A”字样,小灯泡的阻值保持不变,开关S1闭合,S2断开时,灯泡正常发光,则R0的电阻值是________Ω。
8.如图所示,滑动变阻器R2的最大阻值与定值电阻R1相等。闭合开关S,当滑片P在a端时,此时电流表示数为I1;当滑片P在b端时,电流表示数为I2,则I1∶I2=________。
9.如图所示的电路中,电源电压为13.5 V,闭合开关,调节滑动变阻器滑片P从最右端b移动到最左端a,电流表示数由0.18 A变为0.54 A,则滑片位于b点时电压表示数为________V。
10.如图所示,电源电压不变。闭合开关S,移动滑动变阻器的滑片P至某一位置时,电流表的示数为I1;移动滑片P至另一位置时,电流表的示数为I2,电压表示数为1 V。若I1:I2=4:3,前后两次滑动变阻器的阻值之比为2:3,则电源电压为________V。
二、选择题(每题2分,共14分)
11.【新题】小明测量不同型号铅笔在纸上涂画所得线条的电阻,实验步骤如下:
(1)用铅笔在纸上画出两段长为15 cm的线条,在其中一段线条上重复涂画3次,另一段6次;
(2)换用不同型号铅笔重复(1)的操作,得到多组等长等宽的线条(如图);
(3)测出每段线条两端的电阻记录在表中。
根据实验数据,可推测电阻最小的是( )
A.① B.② C.③ D.④
12.如图所示,电源电压保持不变,电阻R1:R2=3:4。S闭合时,甲、乙两处接入电压表;S断开时,甲、乙两处接入电流表。则S闭合时甲、乙两处电压表示数之比U甲:U乙与S断开时甲、乙两处电流表示数之比I甲:I乙分别是( )
A.3:4,1:1 B.3:4,3:4 C.3:4,4:3 D.1:4,4:3
(第12题) (第13题)
13.如图所示的钨丝是将一个白炽灯去除玻璃罩制成的,闭合开关S,小灯泡L发光,钨丝不发光,向钨丝吹气时,小灯泡L变亮,用酒精灯给钨丝加热,小灯泡L逐渐变暗直至熄灭,由实验可知( )
A.钨丝的电阻随温度升高而减小
B.向钨丝吹气时,钨丝电阻变小
C.给钨丝加热时,电路中的电流变大
D.小灯泡L发光而钨丝不发光是因为通过钨丝的电流小于小灯泡L的电流
14.某同学在没有电流表的情况下(电源电压未知但不变),利用电压表和已知阻值的定值电阻R0,测量未知电阻Rx阻值,图中不能实现测量Rx阻值的电路图是( )
A B C D
15.如图甲所示,电源电压不变,R2为电阻箱,调节R2时电流表示数I随之变化。如图乙所示的是电阻箱阻值R2与电流表示数的倒数的图象。则定值电阻R1与电源电压U的大小分别为( )
A.5 Ω 30 V
B.5 Ω 2.5 V
C.10 Ω 20 V
D.10 Ω 10 V
16.将电阻R和灯泡L接在图甲所示的电路中,电源电压保持不变。图乙为电阻R和灯泡L的I?U图象。闭合开关S,电流表示数为0.3 A,则电源电压和电阻R的大小分别是( )
A.8 V 6.67 Ω
B.12 V 20 Ω
C.8 V 20 Ω
D.12 V 10 Ω
(第16题) (第17题)
甲同学 乙同学 丙同学
电流表读数I/A 0.2 0.15 0.12
电压表读数U/V 2 3 3.6
身高h/m
1.6
17.上图是小明设计的一个简易电子身高测量仪的示意图。其中,电源电压恒为6 V,保护电阻R0=20 Ω,R是一只固定着的、竖直放置的硬电阻棒,总长为40 cm,其接入电路的电阻与接入电路的棒长成正比;金属棒cd和MP(右端P是滑片)与电路接触良好,电阻不计。小明用该测量仪对甲、乙和丙三位同学的身高进行了测量,其数据见上表。若已知乙同学测量时,滑片恰在电阻棒ab的中点位置,则根据题中提供的信息可知( )
A.电阻棒的总电阻是30 Ω
B.甲的身高是1.7 m,丙的身高是1.5 m
C.甲的身高是1.5 m,丙的身高是1.8 m
D.从理论上分析,该测量仪的身高测量范围是1.4~1.8 m
三、实验探究题(第18题8分,第19题12分,共20分)
18.某实验小组在探究“电流跟电压、电阻的关系”,实验器材如图所示,还有阻值分别是5 Ω、10 Ω、15 Ω的电阻。
(1)用笔画线代替导线,连接实验电路。要求:滑动变阻器滑片向左移动时,电流表示数增大。
(2)小明按要求正确连接电路后,闭合开关,发现电压表指针偏转到满刻度的位置。其原因可能是________________________。(写出一个即可)
(3)实验中,把定值电阻由5 Ω换成10 Ω,闭合开关后,下一步的操作是:将滑动变阻器的滑片P向__________(填“左”或“右”)移动,目的是_____________。
(第18题) (第19题)
19.在“测未知电阻Rx的阻值”实验中,电路如图甲所示,请完成下列相关问题:
(1)测量时,电压表和电流表的示数记录在表中,得出未知电阻Rx的阻值为________Ω。
实验次序 电压/V 电流/A
1 1.20 0.24
2 1.80 0.36
3 2.40 0.48
(2)另有同学设计了如图甲所示两种测量方案,方案中定值电阻的阻值为R0。
①方案一的电路中,闭合开关S,如果电压表V1和V2的读数分别为U1和U2,则Rx的阻值表达式为Rx=____________;
②方案二的电路中,闭合开关S,如果电流表A1和A2读数分别为I1和I2,则电阻Rx的阻值表达式为Rx=______________。
四、计算题(每题8分,共16分)
20.如果电路上各个电阻的连接方式既不是单纯的串联,也不是单纯的并联,即既有串联,又有并联,则被称为混联。混联电路的总电阻,要根据“先串后并”还是“先并后串”,依据对应的串联、并联电路的规律进行计算。如图所示的混联电路中,电源电压等于6 V,R1=10 Ω,R2=20 Ω,R3=30 Ω,则:
(1)电路中的总电阻为多少?
(2)电流表的示数为多少?
(3)电压表的示数为多少?
21.在实际电路中电流表、电压表的内阻不能忽略。某同学用伏安法测量一个未知电阻Rx,他先将电压表、电流表按图甲所示的方法连接在电源电压恒定的电路中,测得电压表、电流表的示数分别为3.0 V、3.0 mA。接着在同一电路中,他又将同一电压表、电流表按图乙所示的方法连接,测得电压表、电流表的示数分别为2.9 V、4.0 mA。
(1)求出电流表的内阻RA。
(2)求出待测电阻Rx的真实值。
(3)如果电流表的内阻忽略不计,且电压表的内阻不是无限大的。请分析说明题中利用哪种接法测量电阻Rx更准确。
答案
一、1.9∶1 2.30 3. 4.7.5 5.100
6.10 点拨:当电流表并联在R2两端时,R2被短路,R1、R3串联,电流表测电路中的电流,根据欧姆定律可得,电压U=I(R1+R3)=1.5 A×(10 Ω+10 Ω)=30 V;当电流表换成了电压表时,三电阻串联,电压表测R2两端的电压,此时电路中的电流:I′===1 A,电压表的示数:U2=I′R2=1 A×10 Ω=10 V。
7.2.5 点拨:开关S1闭合、S2断开时,灯泡与R0串联,电流表测量电路电流,因为灯泡正常发光,所以电路电流为0.2 A,由I=可得,R总===15 Ω,RL===12.5 Ω,又因为串联电路的总电阻等于各部分电阻之和,所以R0的阻值:R0=R总-RL=15 Ω-12.5 Ω=2.5 Ω。
8.1∶1 9.9
10.4 点拨:由图知,R与变阻器串联,电压表测R两端电压,电流表测电路中电流,若前后两次滑动变阻器的阻值分别为R1、R2,则:=,即:R1=R2,根据串联电路特点和欧姆定律有:I1=,I2=,则:===,化简可得:=。当移动滑片P至另一位置时,电流表的示数为I2,电压表示数为1 V,即:UR=1 V,串联电路中电流处处相等,由欧姆定律知:=,所以U2=×UR=3UR=3×1 V=3 V,所以电源电压:U=U2+UR=3 V+1 V=4 V。
二、11.D 12.B 13.B 14.D
15.B 点拨:由电路图可知,R1与R2串联,电流表测电路中的电流,由图乙可知,当R2=0 Ω时,电路中的电流I1=0.5 A,此时只有R1接入电路,则由I=可得,电源电压U=I1R1=0.5 A×R1;当R2=10 Ω时,电路中的电流I2= A,此时电源电压U=I2(R1+R2)= A×(R1+10 Ω);因电源电压不变,所以0.5 A×R1= A×(R1+10 Ω),解得,R1=5 Ω,电源电压U=I1R1=0.5 A×5 Ω=2.5 V。
16.C
17.D 点拨:由电路图可知,滑动变阻器R与定值电阻R0串联,电流表测电路中的电流,电压表测R两端的电压。乙同学测量时,滑片恰在电阻棒ab的中点位置,由I=可得,此时电阻棒的电阻为R===20 Ω,则电阻棒的总电阻R=40 Ω,故A错误;已知总长为40 cm,所以1 cm的电阻为1 Ω,甲同学量身高时接入电路的电阻为R1===10 Ω,接入电路的长度为h1==10 cm=0.1 m,所以甲同学的身高是1.6 m-0.2 m+0.1 m=1.5 m,丙同学量身高时接入电路的电阻为R2===30 Ω,接入电路的长度为h2==30 cm=0.3 m,所以丙同学的身高是1.6 m-0.2 m+0.3 m=1.7 m,故B、C错误;当滑片在a点时,滑动变阻器全部接入电路,所以测量范围最大是1.6 m-0.2 m+0.4 m=1.8 m,当滑片在b点时,滑动变阻器接入电路电阻为0,所以测量范围最小是1.6 m-0.2 m=1.4 m,则从理论上分析,该测量仪的身高测量范围是1.4~1.8 m,故D正确。
三、18.解:(1)如图所示。
(2)定值电阻断路(合理即可)
(3)右;控制定值电阻两端的电压不变
19.(1)5 (2)①R0 ②
点拨:(1)由表中数据,根据欧姆定律得,R1===5 Ω,同理,R2=5 Ω,R3=5 Ω,故三次测量电阻值的平均值为5 Ω,未知电阻Rx的阻值为5 Ω。
(2)①方案一的电路中,闭合开关S,两电阻串联,电压表V1测R0的电压,电压表V2测未知电阻的电压,如果电压表V1和V2的读数分别为U1和U2,则有=,故Rx的阻值表达式为Rx=R0。
②方案二的电路中,闭合开关S,两电阻并联,A2测定值电阻的电流,A1测干路电流:
由欧姆定律得,电源电压:U=I2R0,
根据并联电路电流的规律,通过待测电阻的电流为Ix=I1-I2,
由欧姆定律得,未知电阻Rx的阻值表达式为Rx==。
四、20.解:(1)R1和R2串联后总电阻R′=R1+R2=10 Ω+20 Ω=30 Ω,R′与R3并联,电路中总电阻为R,=+=+=,得R=15 Ω。
(2)电流表测干路电流,示数为I===0.4 A。
(3)R1和R2串联,该支路两端电压等于电源电压,该支路电流I′===0.2 A,电压表测量R2两端电压;示数为U2=I′R2=0.2 A×20 Ω=4 V。
21.解:(1)图甲中,电压表测量电源电压,电流表测通过电阻Rx的电流,因为图甲中电压表的示数为3.0 V,所以电源电压U=3.0 V,即UA+Ux=3.0 V,图乙中,电压表测量电阻Rx两端的电压,电流表测量通过电阻Rx和电压表的总电流,图乙中电压表的示数为2.9 V,即Ux=2.9 V,所以电流表分得的电压:UA=U-Ux=3.0 V-2.9 V=0.1 V,而IA=4.0 mA,电流表的内阻:RA===25 Ω。
(2)电源电压U=3.0 V,图甲中电流I=3.0 mA,电流表与Rx的总电阻:R===1 000 Ω,即RA+Rx=1 000 Ω,则待测电阻Rx的真实值:Rx=1 000 Ω-RA=1 000 Ω-25 Ω=975 Ω。
(3)在图甲中,如果电流表的内阻忽略不计(即电流表的内阻为零),根据串联电路的分压规律可知,电流表分得的电压为零,电压表测量Rx两端的电压,电流表测量通过Rx的电流,则测得的电阻值准确。
在图乙中,如果电压表的内阻不是无限大的,根据并联电路的分流规律可知,电压表要分得一部分电流,则电流表测得的电流偏大,电压表测量Rx两端的电压,根据R=知,测得的电阻值偏小。
综上所述,如果电流表的内阻忽略不计,且电压表的内阻不是无限大的,利用图甲的测量方法更准确。
同课章节目录
- 第十一章 机械功与机械能
- 11.1 怎样才叫做功
- 11.2 怎样比较做功的快慢
- 11.3 如何提高机械效率
- 11.4 认识动能和势能
- 第十二章 内能与热机
- 12.1 认识内能
- 12.2 热量和热值
- 12.3 研究物质的比热容
- 12.4 热机与社会发展
- 第十三章 探究简单电路
- 13.1 从闪电谈起
- 13.2 电路的组成和连接方式
- 13.3 怎样认识和测量电流
- 13.4 探究串、并联电路中的电流
- 13.5 怎样认识和测量电压
- 13.6 探究串、并联电路中的电压
- 第十四章 探究欧姆定律
- 14.1 怎样认识电阻
- 14.2 探究欧姆定律
- 14.3 欧姆定律的应用
- 第十五章 电能与电功率
- 15.1 电能与电功
- 15.2 认识电功率
- 15.3 怎样使用电器正常工作
- 15.4 探究焦耳定律
