小学数学苏教版五年级上2.4整理与练习课件(29张PPT)
文档属性
| 名称 | 小学数学苏教版五年级上2.4整理与练习课件(29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 14:03:58 | ||
图片预览






文档简介
整理与练习
(复习课)
二
多边形的面积
平行四边形、三角形、梯形的面积公式是什么?
你学过的面积单位有什么?相互之间的进率是什么?
怎么计算组合图形的面积?怎样估计不规则图形的面积?
复习巩固
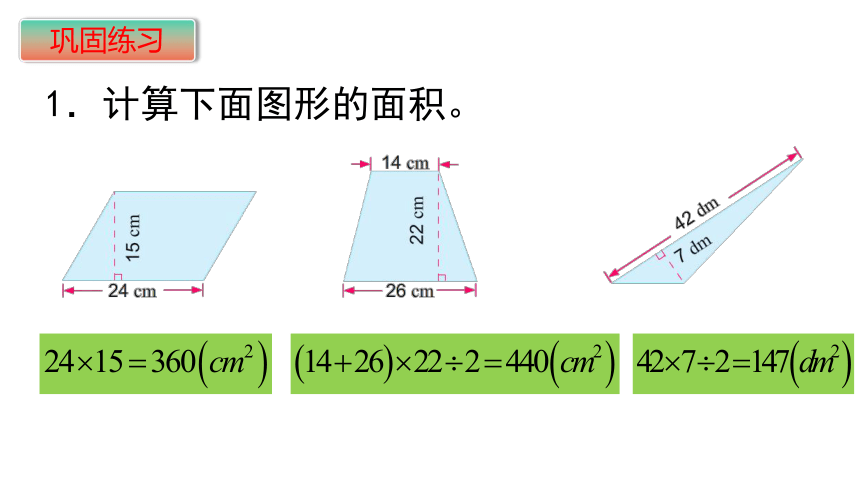
1.计算下面图形的面积。
巩固练习
2.一面用纸做成的直角三角形小旗,两条直角边分别长12厘米和20厘米。做10面这样的小旗,至少需要用纸多少平方厘米?
答:至少需要用纸1200平方厘米。
巩固练习
3.一家自选商店门口的装饰牌是等腰梯形的。它的上底是6米,下底是12米,高是2米。油漆这块装饰牌,每平方米需用油漆1千克,20千克油漆够不够?
答:
20千克油漆够。
(6+12)×2÷2×1=18(千克)
巩固练习
4.
3公顷=(
)平方米
60000平方米=(
)公顷
5平方千米=(
)公顷
700公顷=(
)平方千米
30000
6
500
7
巩固练习
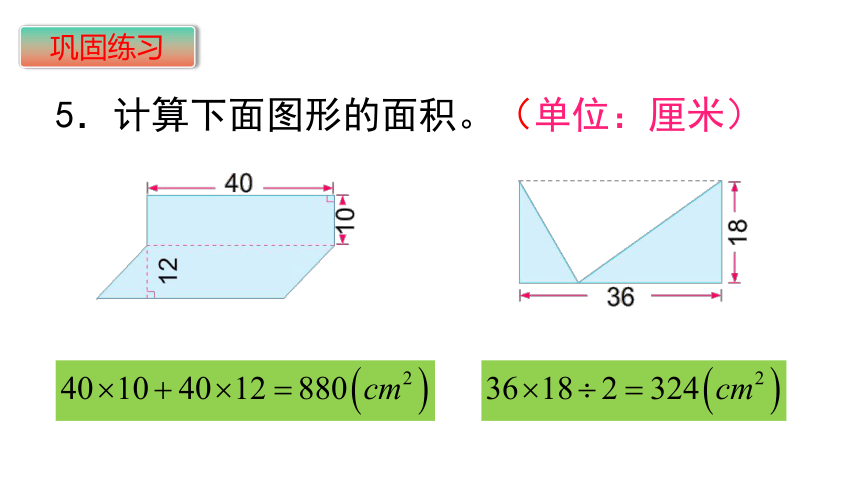
5.计算下面图形的面积。(单位:厘米)
巩固练习
6.一条高速公路的路基长100千米,宽50米。这条公路路基的占地面积大约是多少公顷?是多少平方千米?
答:这条公路路基的占地面积大约是500公顷,是5平方千米。
100千米=100000米
100000×50=5000000(平方米)
5000000平方米=500公顷=5平方千米
巩固练习
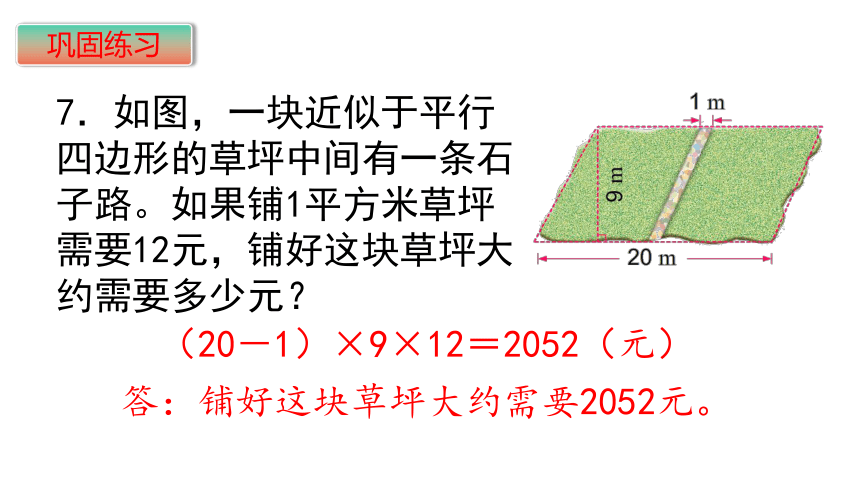
7.如图,一块近似于平行四边形的草坪中间有一条石子路。如果铺1平方米草坪需要12元,铺好这块草坪大约需要多少元?
答:铺好这块草坪大约需要2052元。
(20-1)×9×12=2052(元)
巩固练习
8.一个由8个等腰直角三角形组成的装饰图案(如右图),每个三角形的腰长8分米。这个图案的面积是多少平方分米?
答:这图案的面积是256平方分米。
8×8÷2×8=256(平方分米)
巩固练习
9.把20本练习本摞成一个长方体(如下左图),量出前面长方形的长和宽,算出它的面积。再把这摞练习本均匀地斜放(如下右图),这时前面变成了一个近似的平行四边形,你能测量有关数据,并算出它的面积吗?
巩固练行四边形的底等于长方形的长,平行四边形的高等于长方形的宽,
平行四边形的面积等于长方形的面积。
课后作业
教材P25整理与练习第1题、P26第3题
第
12
课
时
校园绿地面积
(实践活动课)
二
多边形的面积
你们学校的绿地面积是多少?人均绿地面积呢?
要知道学校的人均绿地面积,需要收集哪些数据?可以怎样收集数据?
先了解校园里绿地的分布情况,再制订一个测量和统计校园绿地面积的方案,在全班交流。
要知道校园内草坪、花圃和树木的占地面积。
要计算人均绿地面积,还要知道全校师生人数。
可以查找资料或者实地测量计算面积所需的数据。
新课引入
根据活动方案,分小组测量和计算校园内草坪、花圃和树木的占地面积,并把结果记录在下表中。
例题讲解
汇总各小组的测量结果,并完成下面的统计表。
例题讲解
通过测量和统计,你知道了什么?还能想到哪些问题?
各种类型的绿地中,面积最大的是……
我们学校的人均绿地面积是……
与前几年比,学校的绿地面积有什么变化吗?
例题讲解
通过上面的活动,你有什么收获和体会?
测量和计算绿地面积时,要灵活运用学过的面积计算方法。
可以用查找资料、测量等方法收集数据。
要爱护校园里的一草一木。
课堂小结
课后作业
请你测量学校的草地面积
单
元
复
习
二
多边形的面积
学习目标
1.在理解的基础上掌握平行四边形、三角形和梯形的面积计算公式,能够正确地计算平行四边形、三角形和梯形的面积。
2.通过动手操作和对图形的观察、比较,发展空间观念,初步了解转化思想在研究平行四边形、三角形和梯形面积时的应用,培养学生的分析、综合、抽象、概括和解决实际问题的能力。
3.了解1公顷和1平方千米的实际大小。
4.比较系统地掌握常用的面积单位,会进行单位间的换算。
1.通过观察、测量、拼摆等实践活动,培养动手操作、分析比较、总结概括以及探究、解决实际问题的能力。
2.将知识学习与生活实际相结合,感受到学习的乐趣,发展创新思维和求异思维。
学习重难点
知识点汇总
多边形
的面积
平行四边形的面积公式
平行四边形的面积=底×高
S=ah
三角形的面积公式
三角形的面积=底×高÷2
S=ah÷2
梯形的面积公式
梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2
公顷和平方千米
1公顷=10000平方米
1平方千米=1000000平方米=100公顷
组合图形的面积
割补法
知识点1:平行四边形的面积
一块平行四边形玻璃,底60厘米,高70厘米,面积是多少平方厘米?
60×70=4200(平方厘米)
答:面积是4200平方厘米。
分析
平行四边形的面积=底×高,即S=ah。
注意:计算平行四边形的面积时,底和高要互相对应。
问题解决
知识点2:三角形的面积
一个三角形底是8分米,高是7分米。面积大约是多少平方分米?
8×7÷2=28(平方分米)
答:面积大约是28平方分米。
分析
三角形的面积=底×高÷2,即S=a×h÷2。
注意:计算三角形面积时不要忘记除以2。
问题解决
知识点3:梯形的面积
一个梯形的上底是36米,下底是54米,高是40米。这个梯形的面积是多少平方米?
(36+54)×40÷2=1800(平方米)
答:这个梯形的面积是1800平方米。
分析
梯形的面积=(上底+下底)×高÷2,即S=(a+b)×h÷2。
注意:计算梯形的面积时不要忘记除以2。
问题解决
知识点4:公顷和平方千米
17公顷=(
)平方米
45平方千米=(
)公顷
分析
1公顷=10000平方米 1平方千米=100公顷
注意:平方米是较小的土地面积单位,公顷是较大的土地面积单位。
95000000平方米=(
)平方千米
170000
4500
95
问题解决
知识点5:组合图形和不规
则图形的面积
分析
组合图形可以通过分割法、添补法、割补法来计算面积。
不规则图形的面积可以用数方格的方法估算。
(40+20)×10÷2+20×20
=700(cm2)
(单位:cm)
问题解决
课后作业
教材P27整理与练习第11、13题
及思考题
(复习课)
二
多边形的面积
平行四边形、三角形、梯形的面积公式是什么?
你学过的面积单位有什么?相互之间的进率是什么?
怎么计算组合图形的面积?怎样估计不规则图形的面积?
复习巩固
1.计算下面图形的面积。
巩固练习
2.一面用纸做成的直角三角形小旗,两条直角边分别长12厘米和20厘米。做10面这样的小旗,至少需要用纸多少平方厘米?
答:至少需要用纸1200平方厘米。
巩固练习
3.一家自选商店门口的装饰牌是等腰梯形的。它的上底是6米,下底是12米,高是2米。油漆这块装饰牌,每平方米需用油漆1千克,20千克油漆够不够?
答:
20千克油漆够。
(6+12)×2÷2×1=18(千克)
巩固练习
4.
3公顷=(
)平方米
60000平方米=(
)公顷
5平方千米=(
)公顷
700公顷=(
)平方千米
30000
6
500
7
巩固练习
5.计算下面图形的面积。(单位:厘米)
巩固练习
6.一条高速公路的路基长100千米,宽50米。这条公路路基的占地面积大约是多少公顷?是多少平方千米?
答:这条公路路基的占地面积大约是500公顷,是5平方千米。
100千米=100000米
100000×50=5000000(平方米)
5000000平方米=500公顷=5平方千米
巩固练习
7.如图,一块近似于平行四边形的草坪中间有一条石子路。如果铺1平方米草坪需要12元,铺好这块草坪大约需要多少元?
答:铺好这块草坪大约需要2052元。
(20-1)×9×12=2052(元)
巩固练习
8.一个由8个等腰直角三角形组成的装饰图案(如右图),每个三角形的腰长8分米。这个图案的面积是多少平方分米?
答:这图案的面积是256平方分米。
8×8÷2×8=256(平方分米)
巩固练习
9.把20本练习本摞成一个长方体(如下左图),量出前面长方形的长和宽,算出它的面积。再把这摞练习本均匀地斜放(如下右图),这时前面变成了一个近似的平行四边形,你能测量有关数据,并算出它的面积吗?
巩固练行四边形的底等于长方形的长,平行四边形的高等于长方形的宽,
平行四边形的面积等于长方形的面积。
课后作业
教材P25整理与练习第1题、P26第3题
第
12
课
时
校园绿地面积
(实践活动课)
二
多边形的面积
你们学校的绿地面积是多少?人均绿地面积呢?
要知道学校的人均绿地面积,需要收集哪些数据?可以怎样收集数据?
先了解校园里绿地的分布情况,再制订一个测量和统计校园绿地面积的方案,在全班交流。
要知道校园内草坪、花圃和树木的占地面积。
要计算人均绿地面积,还要知道全校师生人数。
可以查找资料或者实地测量计算面积所需的数据。
新课引入
根据活动方案,分小组测量和计算校园内草坪、花圃和树木的占地面积,并把结果记录在下表中。
例题讲解
汇总各小组的测量结果,并完成下面的统计表。
例题讲解
通过测量和统计,你知道了什么?还能想到哪些问题?
各种类型的绿地中,面积最大的是……
我们学校的人均绿地面积是……
与前几年比,学校的绿地面积有什么变化吗?
例题讲解
通过上面的活动,你有什么收获和体会?
测量和计算绿地面积时,要灵活运用学过的面积计算方法。
可以用查找资料、测量等方法收集数据。
要爱护校园里的一草一木。
课堂小结
课后作业
请你测量学校的草地面积
单
元
复
习
二
多边形的面积
学习目标
1.在理解的基础上掌握平行四边形、三角形和梯形的面积计算公式,能够正确地计算平行四边形、三角形和梯形的面积。
2.通过动手操作和对图形的观察、比较,发展空间观念,初步了解转化思想在研究平行四边形、三角形和梯形面积时的应用,培养学生的分析、综合、抽象、概括和解决实际问题的能力。
3.了解1公顷和1平方千米的实际大小。
4.比较系统地掌握常用的面积单位,会进行单位间的换算。
1.通过观察、测量、拼摆等实践活动,培养动手操作、分析比较、总结概括以及探究、解决实际问题的能力。
2.将知识学习与生活实际相结合,感受到学习的乐趣,发展创新思维和求异思维。
学习重难点
知识点汇总
多边形
的面积
平行四边形的面积公式
平行四边形的面积=底×高
S=ah
三角形的面积公式
三角形的面积=底×高÷2
S=ah÷2
梯形的面积公式
梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2
公顷和平方千米
1公顷=10000平方米
1平方千米=1000000平方米=100公顷
组合图形的面积
割补法
知识点1:平行四边形的面积
一块平行四边形玻璃,底60厘米,高70厘米,面积是多少平方厘米?
60×70=4200(平方厘米)
答:面积是4200平方厘米。
分析
平行四边形的面积=底×高,即S=ah。
注意:计算平行四边形的面积时,底和高要互相对应。
问题解决
知识点2:三角形的面积
一个三角形底是8分米,高是7分米。面积大约是多少平方分米?
8×7÷2=28(平方分米)
答:面积大约是28平方分米。
分析
三角形的面积=底×高÷2,即S=a×h÷2。
注意:计算三角形面积时不要忘记除以2。
问题解决
知识点3:梯形的面积
一个梯形的上底是36米,下底是54米,高是40米。这个梯形的面积是多少平方米?
(36+54)×40÷2=1800(平方米)
答:这个梯形的面积是1800平方米。
分析
梯形的面积=(上底+下底)×高÷2,即S=(a+b)×h÷2。
注意:计算梯形的面积时不要忘记除以2。
问题解决
知识点4:公顷和平方千米
17公顷=(
)平方米
45平方千米=(
)公顷
分析
1公顷=10000平方米 1平方千米=100公顷
注意:平方米是较小的土地面积单位,公顷是较大的土地面积单位。
95000000平方米=(
)平方千米
170000
4500
95
问题解决
知识点5:组合图形和不规
则图形的面积
分析
组合图形可以通过分割法、添补法、割补法来计算面积。
不规则图形的面积可以用数方格的方法估算。
(40+20)×10÷2+20×20
=700(cm2)
(单位:cm)
问题解决
课后作业
教材P27整理与练习第11、13题
及思考题
