冀教版数学七年级上册5.4一元一次方程的应用课件(24张ppt)
文档属性
| 名称 | 冀教版数学七年级上册5.4一元一次方程的应用课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-25 12:31:30 | ||
图片预览






文档简介
(共23张PPT)
列方程是解决实际问题的有效途径之一
1、审题:分析题意,找出图中的数量及其关系
2、设元:选择一个适当的未知数用字母表示(如X)
3、列方程:根据找出的相等关系列出方程
4、解方程:求出未知数的值
5、检验:检查求得的值是否正确和符合实际情形
6、答:写出答案
相等关系:A车路程
+
B车路程
=相距路程
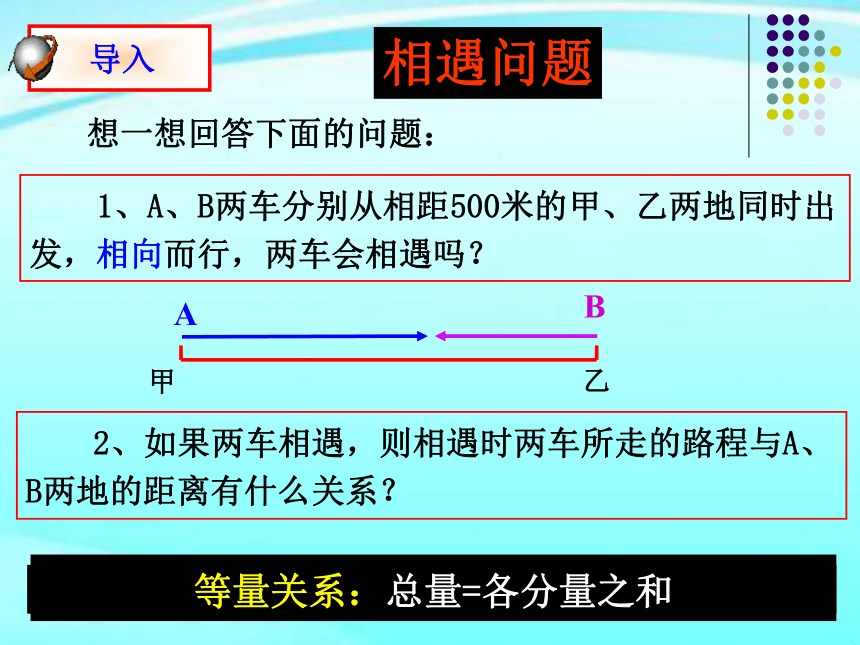
等量关系:总量=各分量之和
想一想回答下面的问题:
1、A、B两车分别从相距500米的甲、乙两地同时出发,相向而行,两车会相遇吗?
导入
甲
乙
A
B
2、如果两车相遇,则相遇时两车所走的路程与A、B两地的距离有什么关系?
相遇问题
想一想回答下面的问题:
3、如果两车同向而行,B车先出发20分钟,在什么情况下两车能相遇?为什么?
A车速度〉B车速度
4、如果A车能追上B车,你能画出线段图吗?
甲
乙
A(B)
等量关系:
B车先行路程
+
B车后行路程
=A车路程
行程问题
一、本课重点
1.基本关系式:_________________
2.基本类型:
相遇问题;
相距问题
3.基本分析方法:画示意图分析题意,分清速度及
时间,找等量关系(路程分成几部分).
4.航行问题的数量关系:
(1)顺流(风)航行的路程=逆流(风)航行的路程
(2)顺水(风)速度=_________________
逆水(风)速度=_________________
路程=速度X时间
静水(无风)速+水(风)速
静水(无风)速—水(风)速
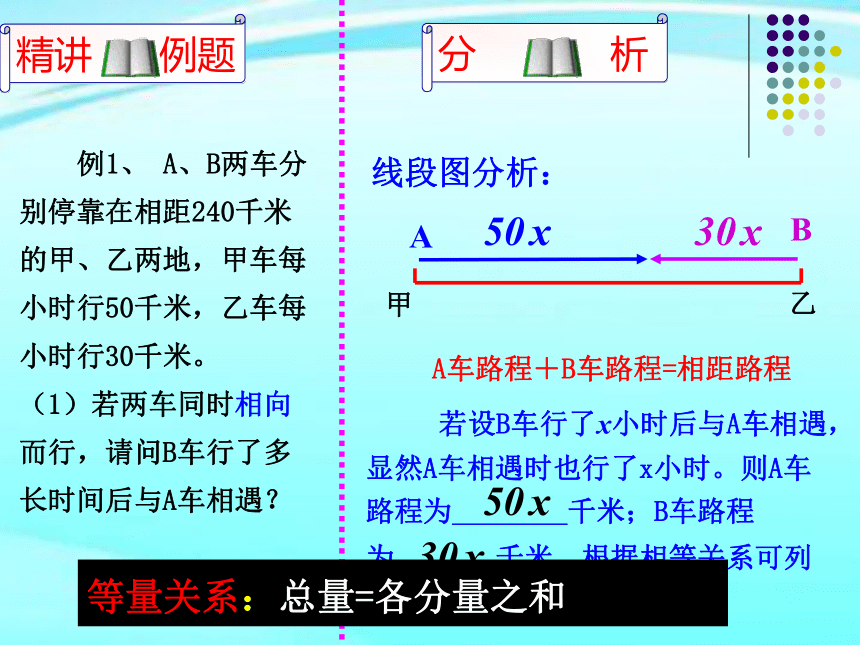
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
精讲
例题
分
析
甲
乙
A
B
A车路程+B车路程=相距路程
线段图分析:
若设B车行了x小时后与A车相遇,显然A车相遇时也行了x小时。则A车路程为
千米;B车路程
为
千米。根据相等关系可列出方程。
等量关系:总量=各分量之和
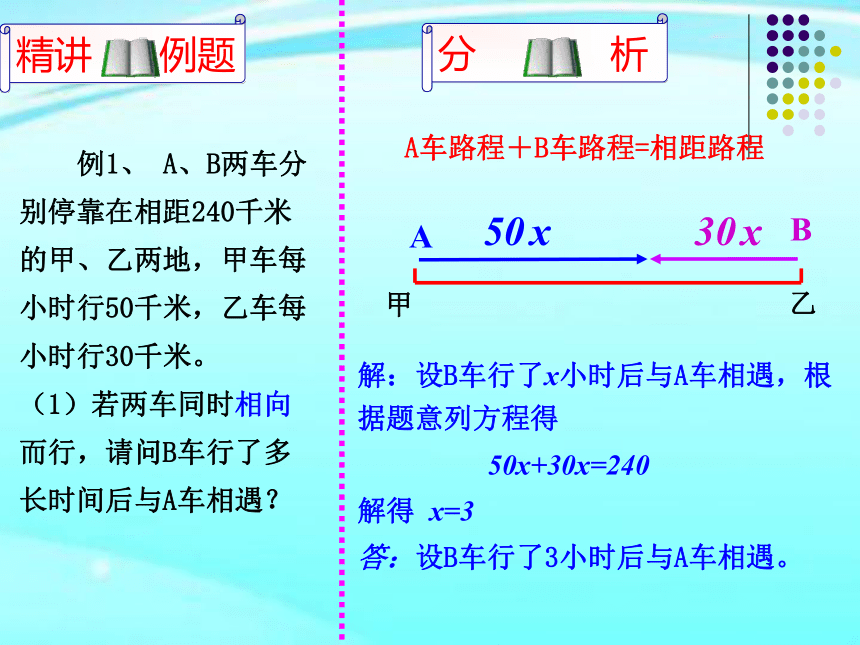
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
精讲
例题
分
析
甲
乙
A
B
A车路程+B车路程=相距路程
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x=240
解得
x=3
答:设B车行了3小时后与A车相遇。
一、相遇问题的基本题型
1、同时出发(两段)
A行的路程+B行的路程=两地距离
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
精讲
例题
分
析
线段图分析:
甲
乙
A
B
80千米
第一种情况:
A车路程+B车路程+相距80千米=
相距路程
等量关系:总量=各分量之和
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
精讲
例题
分
析
线段图分析:
甲
乙
A
B
80千米
第二种情况:
A车路程+B车路程-相距80千米=
相距路程
1、
A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
(1)若两车相向而行,请问B车行了多长时间后与A车相遇?
变式
练习
分
析
等量关系:A车路程+A车同走的路程+
B车同走的路程=相距路程
线段图分析:
甲
乙
A
B
一、相遇问题的基本题型
1、同时出发(两段)
2、不同时出发
(三段
)
先行路程+A行的路程+B行的路程=总路程
A行的路程+B行的路程=两地距离
1、
A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
(2)若两车相向而行,请问B车行了多长时间后两车相距10千米?
变式
练习
分
析
线段图分析:
甲
乙
A
B
甲
乙
A
B
家
学
校
追
及
地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
精讲
例题
分
析
等量关系:
小明先行路程
+
小明后行路程
=爸爸的路程
家
学
校
追
及
地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
精讲
例题
分
析
(1)解:设爸爸要
x分钟才追上小明,依题意得:
180x
=
80x
+
5×80
解得
x=4
答:爸爸追上小明用了4分钟。
相遇问题的基本题型
1、同时出发(两段)
2、不同时出发
(三段
)
先行路程+A行的路程+B行的路程=总路程
A行的路程+B行的路程=两地距离
2、
A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
若两车同向而行(B车在A车前面),请问B车行了多长时间后被A车追上?
变式
练习
分
析
线段图分析:
甲
A
B
50×1.5
50x
30x
乙
115
等量关系:
A车先行路程
+
A车后行路程
-
B车路程
=
115
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
变式
练习
分
析
(1)反向
等量关系:
小王路程
+
叔叔路程
=
400
叔叔
小王
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑4米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
变式
练习
分
析
(2)同向
等量关系:
小王路程
+
400
=
叔叔路程
叔叔
小王
小结:这节课我们复习了行程问题中的相遇和追及问题,归纳如下:
相遇
A车路程
B车路程
等量关系:A车路程+B车路程=相距路程
A车后行路程
B车追击路程
A车先行路程
追及
等量关系:
B车路程=A车先路程+A车后行路程
或B车路程=A车路程+相距路程
归纳:
在列一元一次方程解行程问题时,我们常画出线段图来分析数量关系。用线段图来分析数量关系能够帮助我们更好的理解题意,找到适合题意的等量关系式,设出适合的未知数,列出方程。正确地作出线段图分析数量关系,能使我们分析问题和解问题的能力得到提高。
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
数学问题
(一元一次方程)
实际问题的答案
数学问题的解
(x=a)
列方程
检验
解方程
列方程是解决实际问题的有效途径之一
1、审题:分析题意,找出图中的数量及其关系
2、设元:选择一个适当的未知数用字母表示(如X)
3、列方程:根据找出的相等关系列出方程
4、解方程:求出未知数的值
5、检验:检查求得的值是否正确和符合实际情形
6、答:写出答案
相等关系:A车路程
+
B车路程
=相距路程
等量关系:总量=各分量之和
想一想回答下面的问题:
1、A、B两车分别从相距500米的甲、乙两地同时出发,相向而行,两车会相遇吗?
导入
甲
乙
A
B
2、如果两车相遇,则相遇时两车所走的路程与A、B两地的距离有什么关系?
相遇问题
想一想回答下面的问题:
3、如果两车同向而行,B车先出发20分钟,在什么情况下两车能相遇?为什么?
A车速度〉B车速度
4、如果A车能追上B车,你能画出线段图吗?
甲
乙
A(B)
等量关系:
B车先行路程
+
B车后行路程
=A车路程
行程问题
一、本课重点
1.基本关系式:_________________
2.基本类型:
相遇问题;
相距问题
3.基本分析方法:画示意图分析题意,分清速度及
时间,找等量关系(路程分成几部分).
4.航行问题的数量关系:
(1)顺流(风)航行的路程=逆流(风)航行的路程
(2)顺水(风)速度=_________________
逆水(风)速度=_________________
路程=速度X时间
静水(无风)速+水(风)速
静水(无风)速—水(风)速
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
精讲
例题
分
析
甲
乙
A
B
A车路程+B车路程=相距路程
线段图分析:
若设B车行了x小时后与A车相遇,显然A车相遇时也行了x小时。则A车路程为
千米;B车路程
为
千米。根据相等关系可列出方程。
等量关系:总量=各分量之和
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
精讲
例题
分
析
甲
乙
A
B
A车路程+B车路程=相距路程
解:设B车行了x小时后与A车相遇,根据题意列方程得
50x+30x=240
解得
x=3
答:设B车行了3小时后与A车相遇。
一、相遇问题的基本题型
1、同时出发(两段)
A行的路程+B行的路程=两地距离
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
精讲
例题
分
析
线段图分析:
甲
乙
A
B
80千米
第一种情况:
A车路程+B车路程+相距80千米=
相距路程
等量关系:总量=各分量之和
例1、
A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问B车行了多长时间后两车相距80千米?
精讲
例题
分
析
线段图分析:
甲
乙
A
B
80千米
第二种情况:
A车路程+B车路程-相距80千米=
相距路程
1、
A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
(1)若两车相向而行,请问B车行了多长时间后与A车相遇?
变式
练习
分
析
等量关系:A车路程+A车同走的路程+
B车同走的路程=相距路程
线段图分析:
甲
乙
A
B
一、相遇问题的基本题型
1、同时出发(两段)
2、不同时出发
(三段
)
先行路程+A行的路程+B行的路程=总路程
A行的路程+B行的路程=两地距离
1、
A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
(2)若两车相向而行,请问B车行了多长时间后两车相距10千米?
变式
练习
分
析
线段图分析:
甲
乙
A
B
甲
乙
A
B
家
学
校
追
及
地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
精讲
例题
分
析
等量关系:
小明先行路程
+
小明后行路程
=爸爸的路程
家
学
校
追
及
地
400米
80x米
180x米
例2、小明每天早上要在7:50之前赶到距离家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他。
(1)爸爸追上小明用了多少时间?
(2)追上小明时,距离学校还有多远?
精讲
例题
分
析
(1)解:设爸爸要
x分钟才追上小明,依题意得:
180x
=
80x
+
5×80
解得
x=4
答:爸爸追上小明用了4分钟。
相遇问题的基本题型
1、同时出发(两段)
2、不同时出发
(三段
)
先行路程+A行的路程+B行的路程=总路程
A行的路程+B行的路程=两地距离
2、
A、B两车分别停靠在相距115千米的甲、乙两地,A车每小时行50千米,B车每小时行30千米,A车出发1.5小时后B车再出发。
若两车同向而行(B车在A车前面),请问B车行了多长时间后被A车追上?
变式
练习
分
析
线段图分析:
甲
A
B
50×1.5
50x
30x
乙
115
等量关系:
A车先行路程
+
A车后行路程
-
B车路程
=
115
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
变式
练习
分
析
(1)反向
等量关系:
小王路程
+
叔叔路程
=
400
叔叔
小王
3、小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑4米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
变式
练习
分
析
(2)同向
等量关系:
小王路程
+
400
=
叔叔路程
叔叔
小王
小结:这节课我们复习了行程问题中的相遇和追及问题,归纳如下:
相遇
A车路程
B车路程
等量关系:A车路程+B车路程=相距路程
A车后行路程
B车追击路程
A车先行路程
追及
等量关系:
B车路程=A车先路程+A车后行路程
或B车路程=A车路程+相距路程
归纳:
在列一元一次方程解行程问题时,我们常画出线段图来分析数量关系。用线段图来分析数量关系能够帮助我们更好的理解题意,找到适合题意的等量关系式,设出适合的未知数,列出方程。正确地作出线段图分析数量关系,能使我们分析问题和解问题的能力得到提高。
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
数学问题
(一元一次方程)
实际问题的答案
数学问题的解
(x=a)
列方程
检验
解方程
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
