苏科版数学 九年级上 3.4等腰梯形的判定
文档属性
| 名称 | 苏科版数学 九年级上 3.4等腰梯形的判定 |  | |
| 格式 | zip | ||
| 文件大小 | 152.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-14 18:20:18 | ||
图片预览


文档简介
(共22张PPT)
腰
角
对角线
等腰梯形同一底上的两个角相等
等腰梯形的对角线相等
同一底上的两个角相等的梯形是等腰梯形
对角线相等的梯形是等腰梯形
等腰梯形的两腰相等
两腰相等的梯形是
等腰梯形(定义)
逆命题
等 腰 梯 形 性 质
等腰梯形的判定
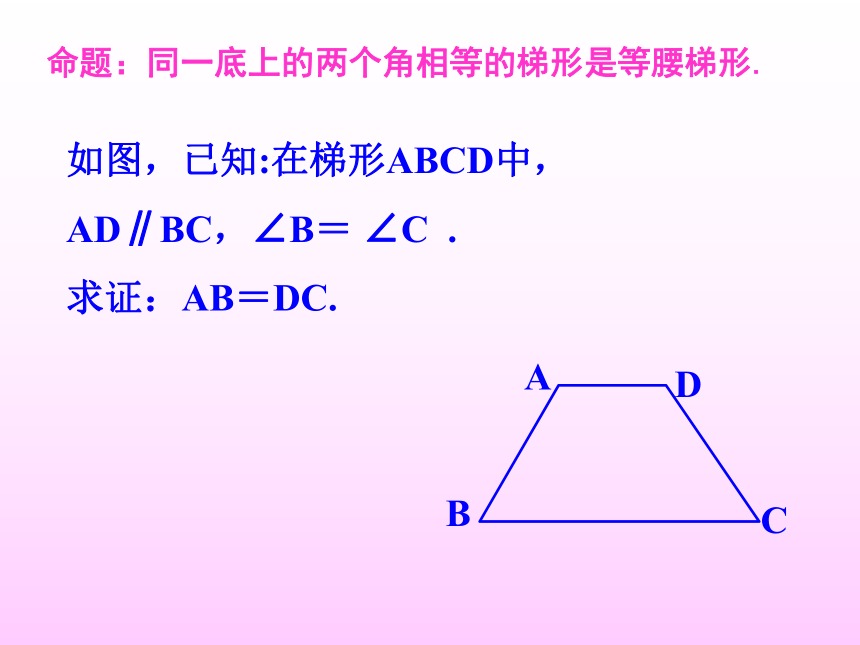
命题:同一底上的两个角相等的梯形是等腰梯形.
A
B
C
D
如图,已知:在梯形ABCD中,
AD∥BC,∠B= ∠C .
求证:AB=DC.
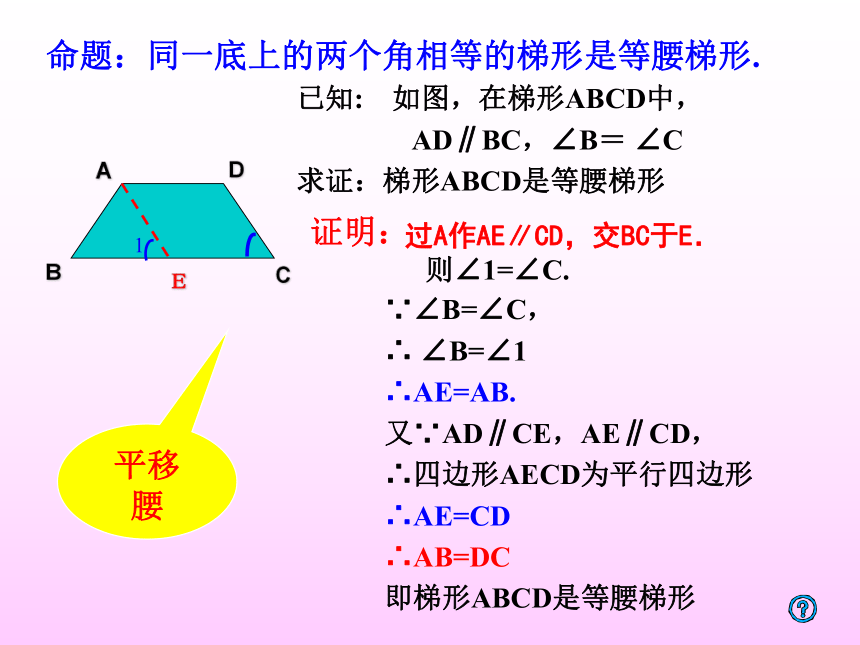
∵∠B=∠C,
∴ ∠B=∠1
∴AE=AB.
又∵AD∥CE,AE∥CD,
∴四边形AECD为平行四边形∴AE=CD
∴AB=DC
即梯形ABCD是等腰梯形
A
B
C
D
已知: 如图,在梯形ABCD中,
AD∥BC,∠B= ∠C
求证:梯形ABCD是等腰梯形
E
过A作AE∥CD,交BC于E.
证明:
命题:同一底上的两个角相等的梯形是等腰梯形.
则∠1=∠C.
平移
腰
1
A
B
C
D
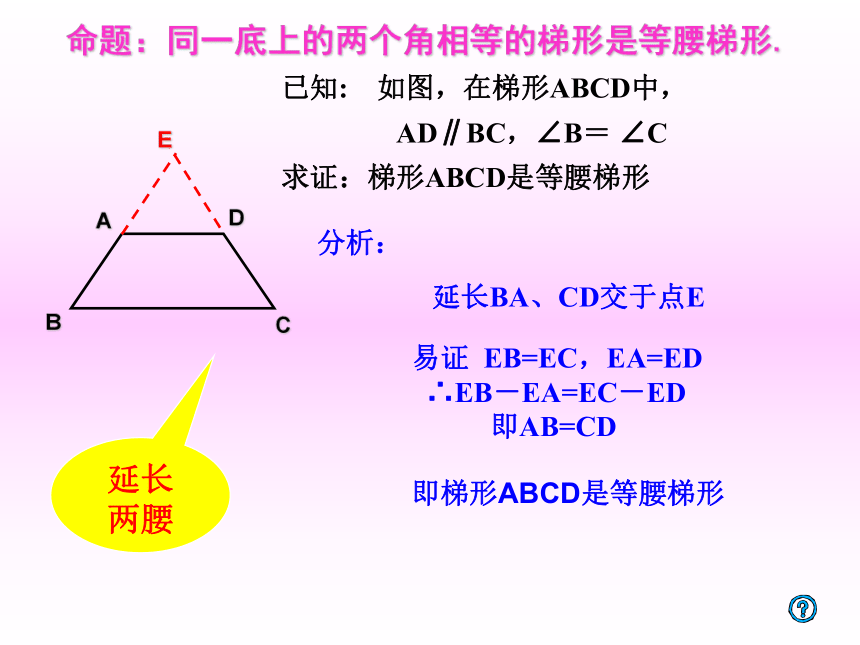
命题:同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B= ∠C
求证:梯形ABCD是等腰梯形
E
易证 EB=EC,EA=ED
∴EB-EA=EC-ED
即AB=CD
延长BA、CD交于点E
即梯形ABCD是等腰梯形
分析:
延长
两腰
A
B
C
D
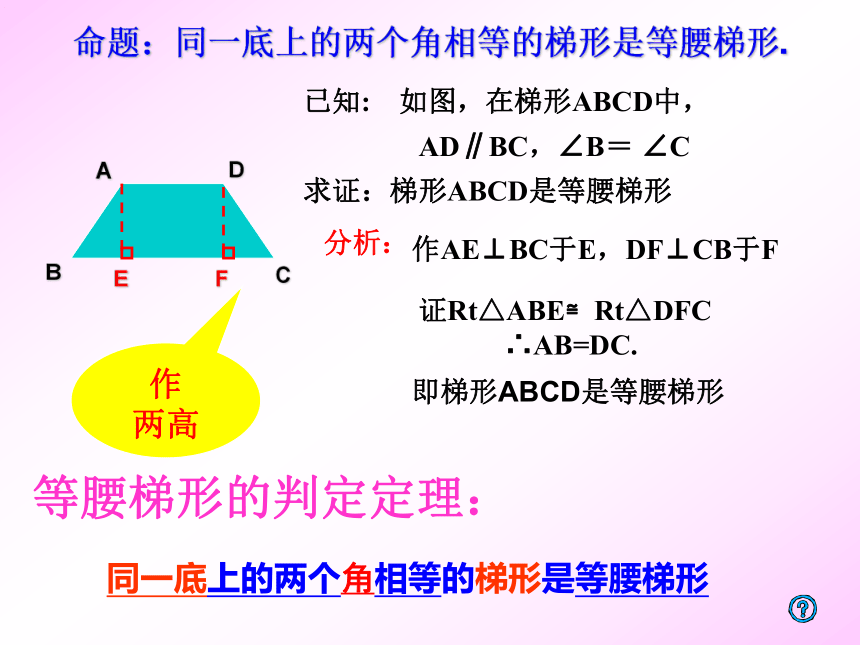
命题:同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B= ∠C
求证:梯形ABCD是等腰梯形
作AE⊥BC于E,DF⊥CB于F
F
证Rt△ABE≌Rt△DFC
∴AB=DC.
E
即梯形ABCD是等腰梯形
分析:
等腰梯形的判定定理:
同一底上的两个角相等的梯形是等腰梯形
作
两高
A
B
C
D
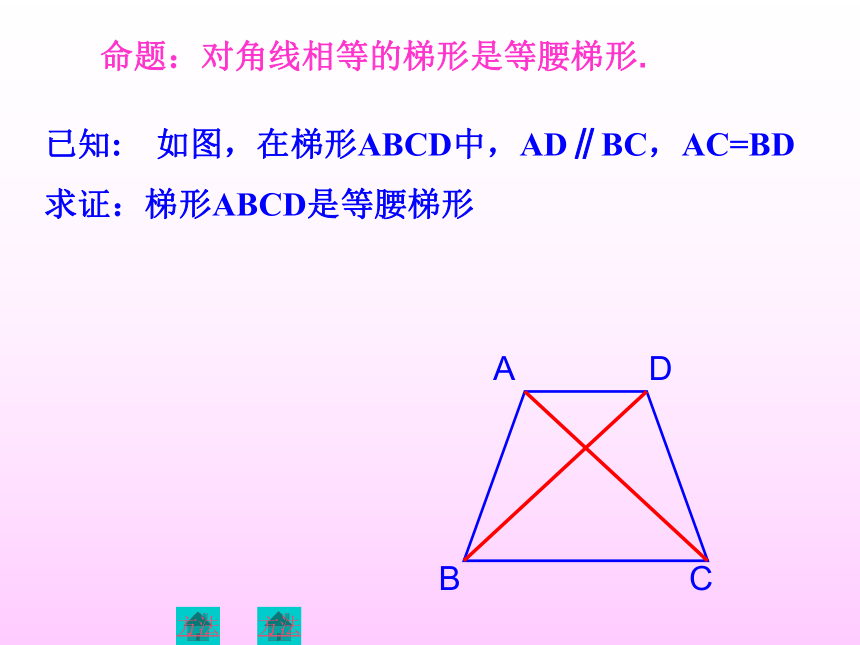
命题:对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
方法
方法
再证△ABC≌△DCB
∴AB=CD
A
B
C
D
证明:
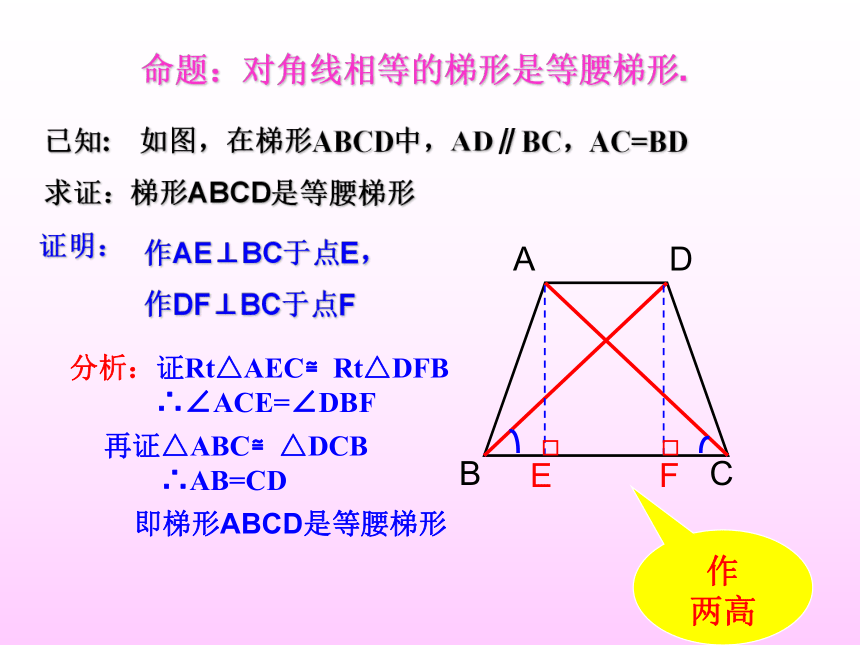
命题:对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
E
F
作AE⊥BC于点E,
作DF⊥BC于点F
分析:证Rt△AEC≌Rt△DFB
∴∠ACE=∠DBF
即梯形ABCD是等腰梯形
作
两高
A
B
C
D
E
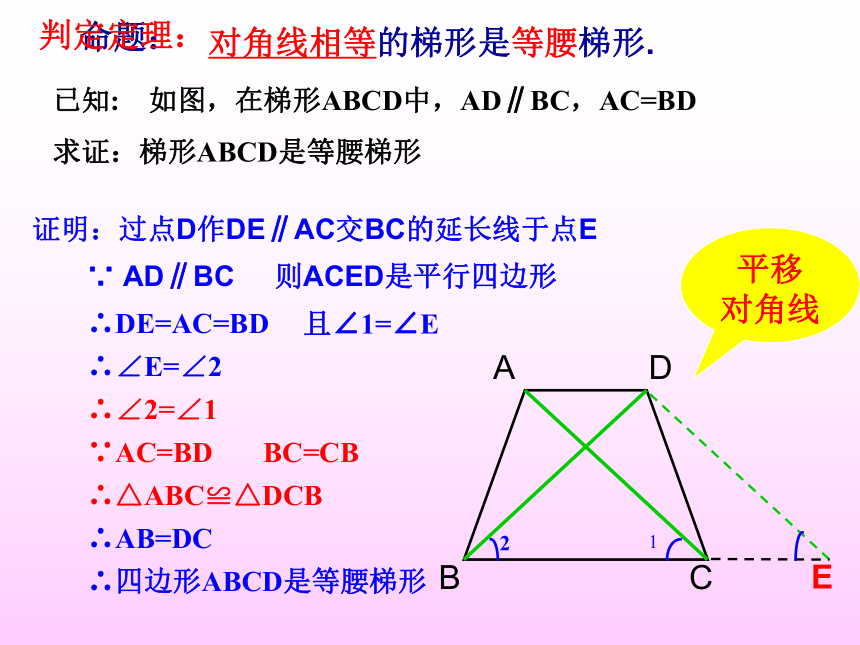
证明:过点D作DE∥AC交BC的延长线于点E
∴DE=AC=BD
∴∠E=∠2
∴∠2=∠1
∵AC=BD BC=CB
∴△ABC≌△DCB
∴AB=DC
∴四边形ABCD是等腰梯形
对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
∵ AD∥BC 则ACED是平行四边形
平移
对角线
命题:
判定定理:
且∠1=∠E
1
2
例 如图: 梯形ABCD中, AD∥BC, DE∥AB,DE=DC,
∠A= 100°。求梯形其他三个内角的度数。
C
B
E
D
A
解:∵ AD∥BC, DE∥AB
∴四边形ABED是平行四边形,
∴ AB=DE
又 DE=DC
∴ AB=DC
梯形ABCD 是等腰梯形;
∴ ∠C= ∠B = 180°- ∠A
= 180°- 100°
= 80°
∠ADC=∠A= 100°.
1.有两个角相等的梯形是( )
A .等腰梯形 B. 直角梯形
C .一般梯形 D.等腰梯形或直角梯形
2.下列命题中:
⑴有两个角相等的梯形是等腰梯形;
⑵有两条边相等的梯形是等腰梯形;
⑶两条对角线相等的梯形是等腰梯形;
⑷等腰梯形上下底边中点的连线 垂直于底边.
其中正确的命题共有( )
A.1个 B.2个 C.3个 D.4个
B
D
3.下列命题是假命题的是( )
A.等腰梯形的两条对角线相等
B.对角线相等的四边形是等腰梯形
C.等腰梯形是轴对称图形
D.梯形的两底之和小于两条对角线之和
B
4.梯形的上、下底分别是2cm,7c m,一腰长为3cm,则另一腰 的长度x的取值范围是____________.
2cmE
A
B
C
D
2
7
3
2
5
3
x
已知: 在梯形ABCD中,AD//BC, E为BC中点,
EF ⊥A B, EG⊥CD,EF=EG。
求证:梯形ABCD为等腰梯形。
A
B
C
D
E
F
G
已知: 在梯形ABCD 中,AD//BC,
∠ACB= ∠DBC.
求证: 梯形ABCD是等腰梯形
A
D
B
C
O
2. 解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为( )问题来解决.
平行四边形和三角形
(1).有两腰相等的梯形是等腰梯形.
(2).同一底上的两个角相等的梯形是等腰梯形.
1.等腰梯形的判定:
(3).对角线相等的梯形是等腰梯形.
一个梯形的上下底的长分别为1,4,对角线
之长为3,4,求这个梯形 的面积。
6
E
1
4
A
B
C
D
1
4
3
4
如图: 在矩形ABCD中,对角线AC、BD
相交于点O,M、N分别是OA、OD的中点
求证:四边形MBCN是等腰梯形
A
B
C
D
O
M
N
如图:在梯形ABCD中,AD∥BC,∠ABC=60°,BD平分∠ABC,BC=2AB.
求证:四边形ABCD是等腰梯形.
想一想
A
B
C
D
拓展训练
A
B
C
Q
D
P
已知:四边形ABCD是直角梯形,AB=8cm,∠B=900
AD=24cm,BC=26cm,点P从A出发,以1cm/s
的速度向D运动,点Q从C出发,以3cm/s的速
度向B运 动,其中一动点达到端点时,另一动
点随之停止运动。从运动开始,经过多少时间,
四边形PQCD是平行四边形?成为等腰梯形?
腰
角
对角线
等腰梯形同一底上的两个角相等
等腰梯形的对角线相等
同一底上的两个角相等的梯形是等腰梯形
对角线相等的梯形是等腰梯形
等腰梯形的两腰相等
两腰相等的梯形是
等腰梯形(定义)
逆命题
等 腰 梯 形 性 质
等腰梯形的判定
命题:同一底上的两个角相等的梯形是等腰梯形.
A
B
C
D
如图,已知:在梯形ABCD中,
AD∥BC,∠B= ∠C .
求证:AB=DC.
∵∠B=∠C,
∴ ∠B=∠1
∴AE=AB.
又∵AD∥CE,AE∥CD,
∴四边形AECD为平行四边形∴AE=CD
∴AB=DC
即梯形ABCD是等腰梯形
A
B
C
D
已知: 如图,在梯形ABCD中,
AD∥BC,∠B= ∠C
求证:梯形ABCD是等腰梯形
E
过A作AE∥CD,交BC于E.
证明:
命题:同一底上的两个角相等的梯形是等腰梯形.
则∠1=∠C.
平移
腰
1
A
B
C
D
命题:同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B= ∠C
求证:梯形ABCD是等腰梯形
E
易证 EB=EC,EA=ED
∴EB-EA=EC-ED
即AB=CD
延长BA、CD交于点E
即梯形ABCD是等腰梯形
分析:
延长
两腰
A
B
C
D
命题:同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B= ∠C
求证:梯形ABCD是等腰梯形
作AE⊥BC于E,DF⊥CB于F
F
证Rt△ABE≌Rt△DFC
∴AB=DC.
E
即梯形ABCD是等腰梯形
分析:
等腰梯形的判定定理:
同一底上的两个角相等的梯形是等腰梯形
作
两高
A
B
C
D
命题:对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
方法
方法
再证△ABC≌△DCB
∴AB=CD
A
B
C
D
证明:
命题:对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
E
F
作AE⊥BC于点E,
作DF⊥BC于点F
分析:证Rt△AEC≌Rt△DFB
∴∠ACE=∠DBF
即梯形ABCD是等腰梯形
作
两高
A
B
C
D
E
证明:过点D作DE∥AC交BC的延长线于点E
∴DE=AC=BD
∴∠E=∠2
∴∠2=∠1
∵AC=BD BC=CB
∴△ABC≌△DCB
∴AB=DC
∴四边形ABCD是等腰梯形
对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
∵ AD∥BC 则ACED是平行四边形
平移
对角线
命题:
判定定理:
且∠1=∠E
1
2
例 如图: 梯形ABCD中, AD∥BC, DE∥AB,DE=DC,
∠A= 100°。求梯形其他三个内角的度数。
C
B
E
D
A
解:∵ AD∥BC, DE∥AB
∴四边形ABED是平行四边形,
∴ AB=DE
又 DE=DC
∴ AB=DC
梯形ABCD 是等腰梯形;
∴ ∠C= ∠B = 180°- ∠A
= 180°- 100°
= 80°
∠ADC=∠A= 100°.
1.有两个角相等的梯形是( )
A .等腰梯形 B. 直角梯形
C .一般梯形 D.等腰梯形或直角梯形
2.下列命题中:
⑴有两个角相等的梯形是等腰梯形;
⑵有两条边相等的梯形是等腰梯形;
⑶两条对角线相等的梯形是等腰梯形;
⑷等腰梯形上下底边中点的连线 垂直于底边.
其中正确的命题共有( )
A.1个 B.2个 C.3个 D.4个
B
D
3.下列命题是假命题的是( )
A.等腰梯形的两条对角线相等
B.对角线相等的四边形是等腰梯形
C.等腰梯形是轴对称图形
D.梯形的两底之和小于两条对角线之和
B
4.梯形的上、下底分别是2cm,7c m,一腰长为3cm,则另一腰 的长度x的取值范围是____________.
2cm
A
B
C
D
2
7
3
2
5
3
x
已知: 在梯形ABCD中,AD//BC, E为BC中点,
EF ⊥A B, EG⊥CD,EF=EG。
求证:梯形ABCD为等腰梯形。
A
B
C
D
E
F
G
已知: 在梯形ABCD 中,AD//BC,
∠ACB= ∠DBC.
求证: 梯形ABCD是等腰梯形
A
D
B
C
O
2. 解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为( )问题来解决.
平行四边形和三角形
(1).有两腰相等的梯形是等腰梯形.
(2).同一底上的两个角相等的梯形是等腰梯形.
1.等腰梯形的判定:
(3).对角线相等的梯形是等腰梯形.
一个梯形的上下底的长分别为1,4,对角线
之长为3,4,求这个梯形 的面积。
6
E
1
4
A
B
C
D
1
4
3
4
如图: 在矩形ABCD中,对角线AC、BD
相交于点O,M、N分别是OA、OD的中点
求证:四边形MBCN是等腰梯形
A
B
C
D
O
M
N
如图:在梯形ABCD中,AD∥BC,∠ABC=60°,BD平分∠ABC,BC=2AB.
求证:四边形ABCD是等腰梯形.
想一想
A
B
C
D
拓展训练
A
B
C
Q
D
P
已知:四边形ABCD是直角梯形,AB=8cm,∠B=900
AD=24cm,BC=26cm,点P从A出发,以1cm/s
的速度向D运动,点Q从C出发,以3cm/s的速
度向B运 动,其中一动点达到端点时,另一动
点随之停止运动。从运动开始,经过多少时间,
四边形PQCD是平行四边形?成为等腰梯形?
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
