人教版A高中数学必修1 课件 2.3幂函数(共31张PPT)
文档属性
| 名称 | 人教版A高中数学必修1 课件 2.3幂函数(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
2.3幂函数
二次函数与幂函数
1.幂函数
(1)幂函数的定义是什么?
提示:形如y=xα(α∈R)的函数称为幂函数,其中x为自变量.
α为常数
(2)有哪五种常用幂函数?
2.二次函数解析式的三种常用表达形式
(1)一般式:f(x)=_______________________;
(2)顶点式:f(x)=a(x-h)2+k(a≠0),(h,k)是顶点;
(3)零点式(或因式分解式):f(x)=a(x-x1)(x-x2)(a≠0),
其
中x1,x2分别是f(x)=0的两实根.
ax2+bx+c(a≠0)
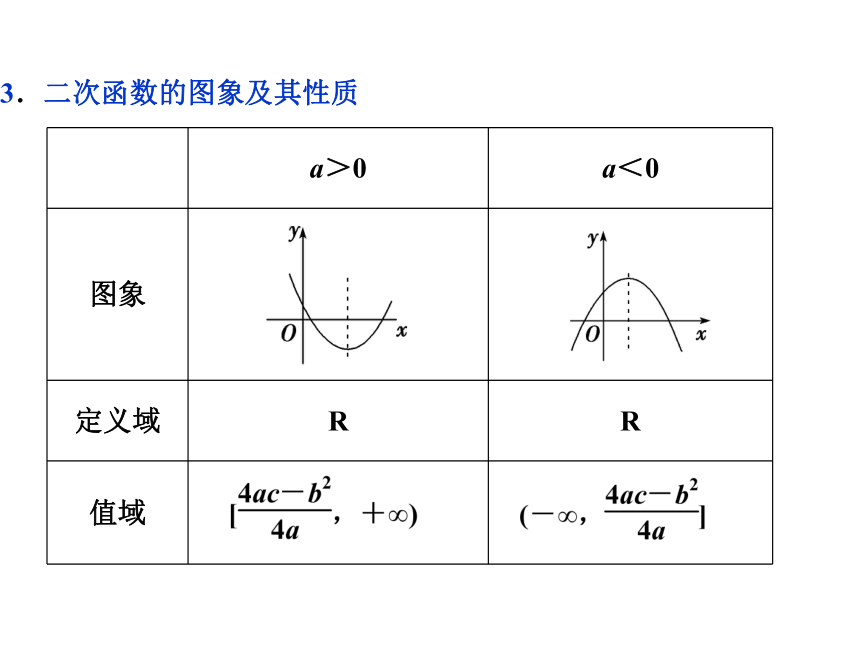
3.二次函数的图象及其性质
a>0
a<0
图象
定义域
R
R
值域
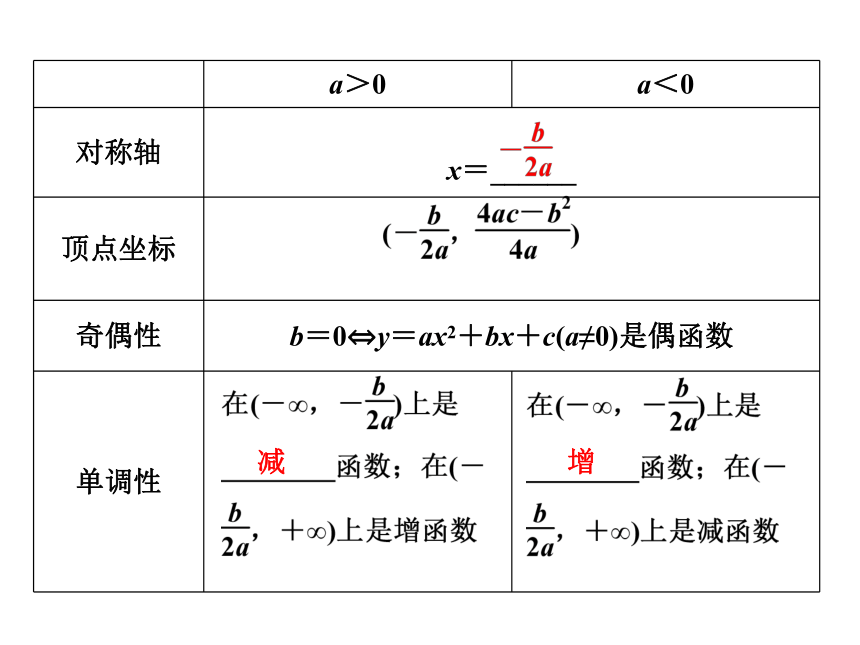
a>0
a<0
对称轴
x=______
顶点坐标
奇偶性
b=0?y=ax2+bx+c(a≠0)是偶函数
单调性
减
增
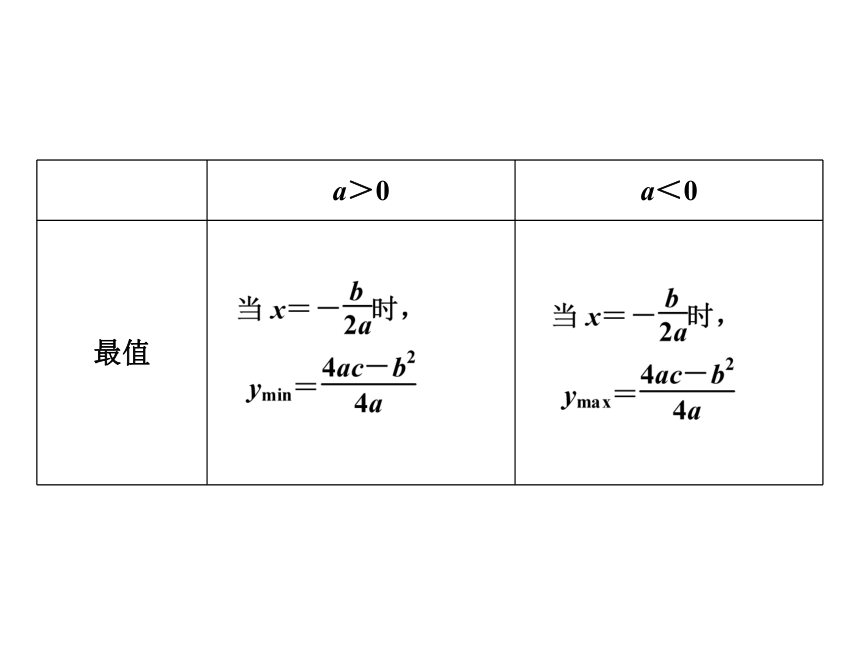
a>0
a<0
最值
C
B
D
4.如果函数f(x)=x2+(a+2)x+b(x∈[a,b])的图象关于直线x=1对称,则函数f(x)的最小值为________.
5
(-∞,0)∪(0,+∞)
奇函数
(-∞,0)和(0,+∞)
二次函数的解析式
[课堂笔记]
在求二次函数解析式时,要灵活地选择二次函数解析式
的
表达形式:
(1)已知三个点的坐标,应选择一般形式;
(2)已知顶点坐标或对称轴或最值,应选择顶点式;
(3)已知函数图象与x轴的交点坐标,应选择零点式.
注意:求二次函数的解析式时,如果选用的形式
不当、引
入的字母系数过多,会加大运算量,易出错.
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调
函数;
(3)当a=1时,求f(|x|)的单调区间.
[课堂笔记]
二次函数的图象与性质
(1)二次函数在闭区间上的最值主要有三种类型:轴定区间
定、轴动区间定、轴定区间动,不论哪种类型,解决的
关
键是考察对称轴与区间的位置关系,当含有参数时,要依
据
对称轴与区间的位置关系进行分类讨论;(2)二次函数的单调
性问题则主要依据二次函数图象的对称轴进行分类讨论求解.
2.已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值
2,求a的值.
幂函数的图象与性质
[课堂笔记]
-1
2
-1
分类讨论思想在求二次函数最值中的应用
(1)本题在求二次函数最值时,用到了分类讨论思
想,
求
解中既对系数a进行了讨论,又对对称轴进行讨论.在
分类讨论时要遵循分类的原则:一是分类的标准要一
致,二
是
分类时要做到不重不漏,三是能不分类的要尽量避免分
类,
绝不无原则的分类讨论.
(2)在有关二次函数最值的求解中,若轴定区
间动,仍
应
对区间进行分类讨论.
设函数y=x2-2x,x∈[-2,a],求函数的最小值g(a).
2.3幂函数
二次函数与幂函数
1.幂函数
(1)幂函数的定义是什么?
提示:形如y=xα(α∈R)的函数称为幂函数,其中x为自变量.
α为常数
(2)有哪五种常用幂函数?
2.二次函数解析式的三种常用表达形式
(1)一般式:f(x)=_______________________;
(2)顶点式:f(x)=a(x-h)2+k(a≠0),(h,k)是顶点;
(3)零点式(或因式分解式):f(x)=a(x-x1)(x-x2)(a≠0),
其
中x1,x2分别是f(x)=0的两实根.
ax2+bx+c(a≠0)
3.二次函数的图象及其性质
a>0
a<0
图象
定义域
R
R
值域
a>0
a<0
对称轴
x=______
顶点坐标
奇偶性
b=0?y=ax2+bx+c(a≠0)是偶函数
单调性
减
增
a>0
a<0
最值
C
B
D
4.如果函数f(x)=x2+(a+2)x+b(x∈[a,b])的图象关于直线x=1对称,则函数f(x)的最小值为________.
5
(-∞,0)∪(0,+∞)
奇函数
(-∞,0)和(0,+∞)
二次函数的解析式
[课堂笔记]
在求二次函数解析式时,要灵活地选择二次函数解析式
的
表达形式:
(1)已知三个点的坐标,应选择一般形式;
(2)已知顶点坐标或对称轴或最值,应选择顶点式;
(3)已知函数图象与x轴的交点坐标,应选择零点式.
注意:求二次函数的解析式时,如果选用的形式
不当、引
入的字母系数过多,会加大运算量,易出错.
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调
函数;
(3)当a=1时,求f(|x|)的单调区间.
[课堂笔记]
二次函数的图象与性质
(1)二次函数在闭区间上的最值主要有三种类型:轴定区间
定、轴动区间定、轴定区间动,不论哪种类型,解决的
关
键是考察对称轴与区间的位置关系,当含有参数时,要依
据
对称轴与区间的位置关系进行分类讨论;(2)二次函数的单调
性问题则主要依据二次函数图象的对称轴进行分类讨论求解.
2.已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值
2,求a的值.
幂函数的图象与性质
[课堂笔记]
-1
2
-1
分类讨论思想在求二次函数最值中的应用
(1)本题在求二次函数最值时,用到了分类讨论思
想,
求
解中既对系数a进行了讨论,又对对称轴进行讨论.在
分类讨论时要遵循分类的原则:一是分类的标准要一
致,二
是
分类时要做到不重不漏,三是能不分类的要尽量避免分
类,
绝不无原则的分类讨论.
(2)在有关二次函数最值的求解中,若轴定区
间动,仍
应
对区间进行分类讨论.
设函数y=x2-2x,x∈[-2,a],求函数的最小值g(a).
