六年级下册数学课件-3.2正比例的应用 西师大版(17张ppt)
文档属性
| 名称 | 六年级下册数学课件-3.2正比例的应用 西师大版(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 398.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-25 05:44:55 | ||
图片预览





文档简介
正比例的应用
复习
判断下面每题中的两种量成什么比例?
(1)速度一定,路程和时间.
正比例
(2)工作时间一定,工作效率和工作总量.
正比例
(3)单价一定,总价和数量.
正比例
(4)每小时耕地的公顷数一定,耕地的总公顷数和时间.
正比例
据疑研讨
汇报自学情况
据疑研讨
小组合作释疑
认真看课本第44页的内容,探讨下面几个问题:
3、在运用正比例知识解决问题时,应注意些什么?
2、例3中哪种量是一定?
1、例题3中涉及哪三种量?
把你学到的知识分享给大家
持疑分享
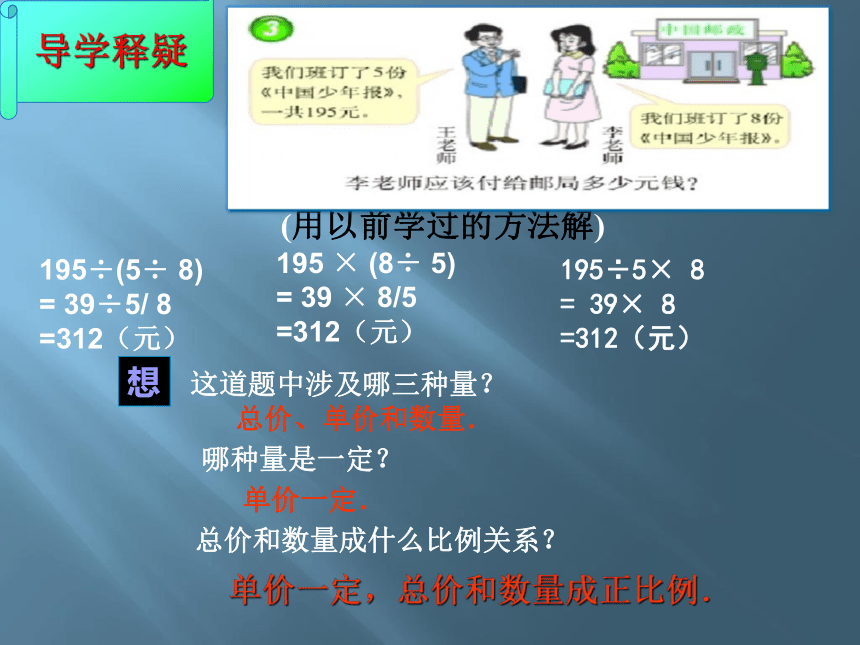
导学释疑
(用以前学过的方法解)
195÷5× 8
= 39× 8
=312(元)
想
这道题中涉及哪三种量?
哪种量是一定?
总价和数量成什么比例关系?
总价、单价和数量.
单价一定.
单价一定,总价和数量成正比例.
195÷(5÷ 8)
= 39÷5/ 8
=312(元)
195 × (8÷ 5)
= 39 × 8/5
=312(元)
导
学
释
疑
一辆汽车2小时行驶140千米,照这样的速度,
从
甲地到乙地共行驶5小时.甲乙两地之间的公路长多
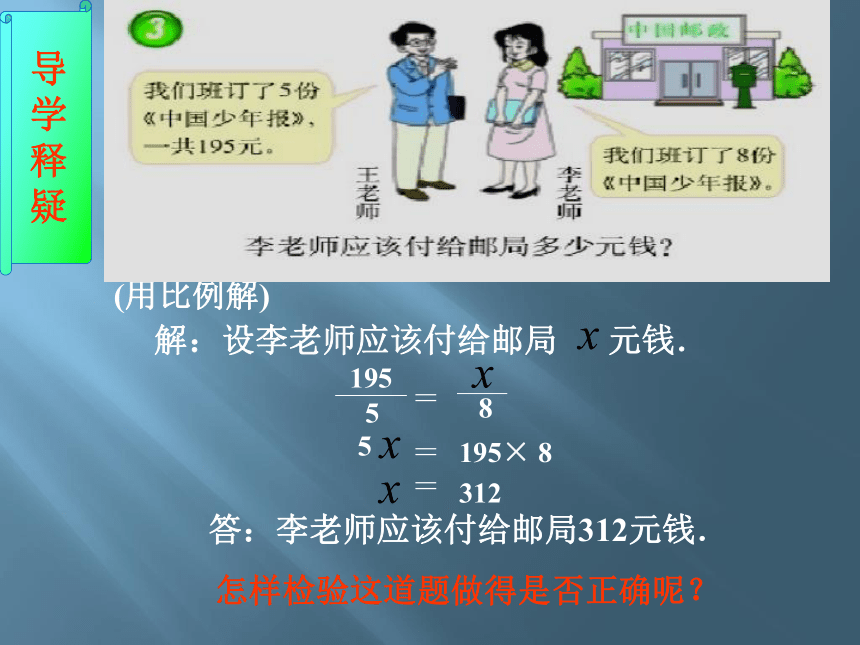
(用比例解)
解:设李老师应该付给邮局 元钱.
195
5
8
=
5
=
195× 8
=
312
怎样检验这道题做得是否正确呢?
答:李老师应该付给邮局312元钱.
变式
王老师为班上订了5份《中国先锋报》,共用人民币195元,李老师用人民币312元,可以订多少份《中国先锋报》?
解:设可以订 份《中国先锋报》。
195
5
=
195
=
312×5
=
8
312
答:可以订 8 份《中国先锋报》 。
导学释疑
用比例知识解答应用题的关键:先找出题中的两种相关联的量,判断它们是否是正比例关系,然后根据正反比例的意义列出方程.
用比例解决问题的具体步骤:
1、分析判断,
2、找出列比例式所需的相等关系,
3、设未知数等式,
4、求解,
5、检验后写出答语。
导学释疑
食堂买3桶油用780元,照这样计算,买8桶油要用多少元?
(用比例知识解答)
解:设买8桶油要用 元.
答:买8桶油要用2080元.
练习解疑
780
3
=
3
=
780×8
=
2080
8
每桶油的单价一定,总价和数量成正比例.
竹笋的生长很快,现在已知一株竹笋3天可以长到12厘米,如果它匀速生长,那么它18天可以长到多少厘米?(用比例知识解答)
解:设它18天可以长到 厘米.
答:它18天可以长到 72 厘米.
12
3
=
3
=
12×18
=
72
18
增长速度一定,生长的时间和生长的长度成正比例.
练习释疑
修路队修了一条公路,已修部分与未修部分的比5:3,又知已修部分比未修部份长600米,这条路长多少米?(用比例知识解答)
拓展释疑
拓展练习
(一提多解尽自己的能力)
为给希望工程捐款,东东和小力卖废品共收入14.4元,小力卖废品的钱是东东的4/5,求东东应收多少钱的废品费?
方法一:用比例来解答
解:设东东应收x元废品钱。
14.4:(4+5)=x:5
9x=14.4×5
X=72÷9
X=8
答:东东应收8元废品钱。
方法二:按分数比解
解:东东拾得废品费:小力拾得废品费=5:4 ,那么设东东应收5x元废品钱,小力应收4x 元废品钱。
5x+ 4x=14.4
9x=14.4
X=1.6
5x=5×1.6=8(元)
答:东东应收8元废品钱。
这节课你有哪些收获?
谢谢孩子们!
复习
判断下面每题中的两种量成什么比例?
(1)速度一定,路程和时间.
正比例
(2)工作时间一定,工作效率和工作总量.
正比例
(3)单价一定,总价和数量.
正比例
(4)每小时耕地的公顷数一定,耕地的总公顷数和时间.
正比例
据疑研讨
汇报自学情况
据疑研讨
小组合作释疑
认真看课本第44页的内容,探讨下面几个问题:
3、在运用正比例知识解决问题时,应注意些什么?
2、例3中哪种量是一定?
1、例题3中涉及哪三种量?
把你学到的知识分享给大家
持疑分享
导学释疑
(用以前学过的方法解)
195÷5× 8
= 39× 8
=312(元)
想
这道题中涉及哪三种量?
哪种量是一定?
总价和数量成什么比例关系?
总价、单价和数量.
单价一定.
单价一定,总价和数量成正比例.
195÷(5÷ 8)
= 39÷5/ 8
=312(元)
195 × (8÷ 5)
= 39 × 8/5
=312(元)
导
学
释
疑
一辆汽车2小时行驶140千米,照这样的速度,
从
甲地到乙地共行驶5小时.甲乙两地之间的公路长多
(用比例解)
解:设李老师应该付给邮局 元钱.
195
5
8
=
5
=
195× 8
=
312
怎样检验这道题做得是否正确呢?
答:李老师应该付给邮局312元钱.
变式
王老师为班上订了5份《中国先锋报》,共用人民币195元,李老师用人民币312元,可以订多少份《中国先锋报》?
解:设可以订 份《中国先锋报》。
195
5
=
195
=
312×5
=
8
312
答:可以订 8 份《中国先锋报》 。
导学释疑
用比例知识解答应用题的关键:先找出题中的两种相关联的量,判断它们是否是正比例关系,然后根据正反比例的意义列出方程.
用比例解决问题的具体步骤:
1、分析判断,
2、找出列比例式所需的相等关系,
3、设未知数等式,
4、求解,
5、检验后写出答语。
导学释疑
食堂买3桶油用780元,照这样计算,买8桶油要用多少元?
(用比例知识解答)
解:设买8桶油要用 元.
答:买8桶油要用2080元.
练习解疑
780
3
=
3
=
780×8
=
2080
8
每桶油的单价一定,总价和数量成正比例.
竹笋的生长很快,现在已知一株竹笋3天可以长到12厘米,如果它匀速生长,那么它18天可以长到多少厘米?(用比例知识解答)
解:设它18天可以长到 厘米.
答:它18天可以长到 72 厘米.
12
3
=
3
=
12×18
=
72
18
增长速度一定,生长的时间和生长的长度成正比例.
练习释疑
修路队修了一条公路,已修部分与未修部分的比5:3,又知已修部分比未修部份长600米,这条路长多少米?(用比例知识解答)
拓展释疑
拓展练习
(一提多解尽自己的能力)
为给希望工程捐款,东东和小力卖废品共收入14.4元,小力卖废品的钱是东东的4/5,求东东应收多少钱的废品费?
方法一:用比例来解答
解:设东东应收x元废品钱。
14.4:(4+5)=x:5
9x=14.4×5
X=72÷9
X=8
答:东东应收8元废品钱。
方法二:按分数比解
解:东东拾得废品费:小力拾得废品费=5:4 ,那么设东东应收5x元废品钱,小力应收4x 元废品钱。
5x+ 4x=14.4
9x=14.4
X=1.6
5x=5×1.6=8(元)
答:东东应收8元废品钱。
这节课你有哪些收获?
谢谢孩子们!
