课件:三角形的内切圆
图片预览

文档简介
(共9张PPT)
三角形的内切圆
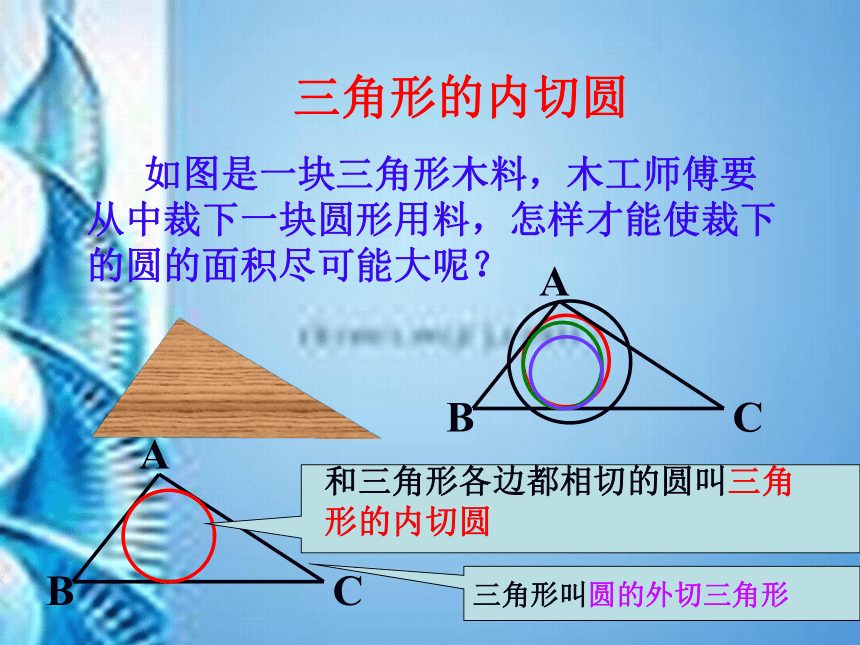
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
A
B
C
三角形的内切圆
A
B
C
和三角形各边都相切的圆叫三角形的内切圆
三角形叫圆的外切三角形
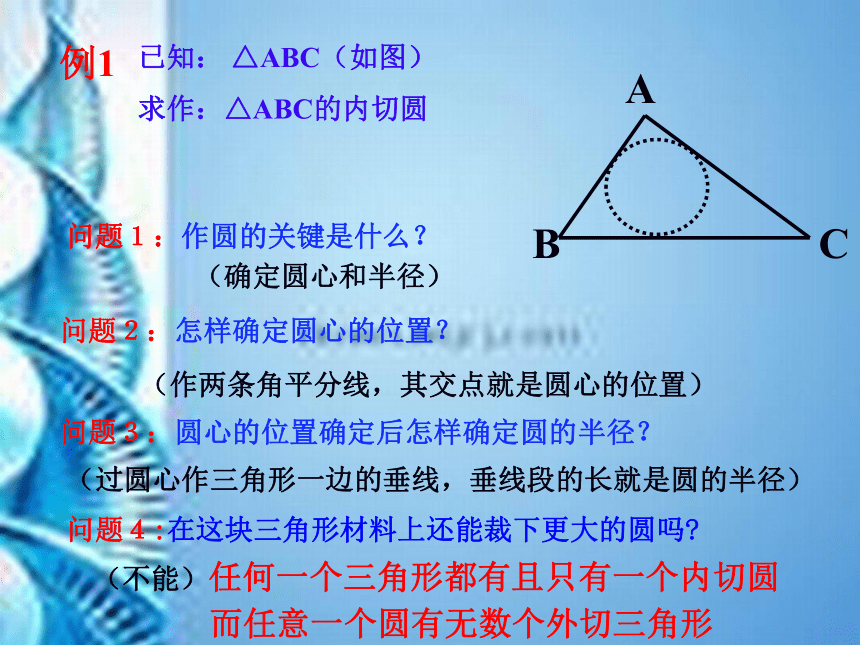
问题1:作圆的关键是什么?
问题2:怎样确定圆心的位置?
问题3:圆心的位置确定后怎样确定圆的半径?
A
B
C
(确定圆心和半径)
(作两条角平分线,其交点就是圆心的位置)
(过圆心作三角形一边的垂线,垂线段的长就是圆的半径)
例1
已知: △ABC(如图)
求作:△ABC的内切圆
问题4:在这块三角形材料上还能裁下更大的圆吗
(不能)任何一个三角形都有且只有一个内切圆
而任意一个圆有无数个外切三角形
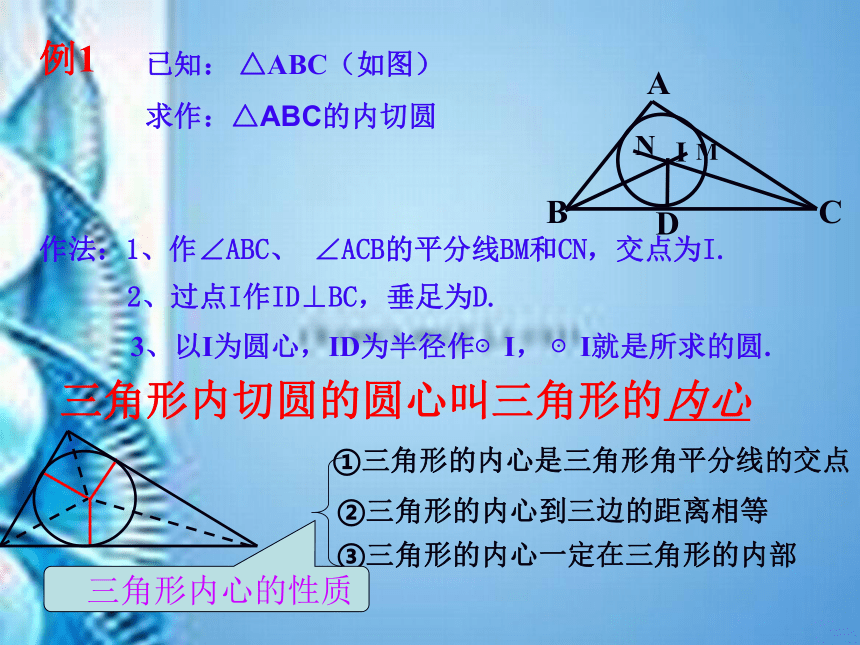
3、以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆.
例1
已知: △ABC(如图)
求作:△ABC的内切圆
A
B
C
M
N
I
D
作法:1、作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
三角形内切圆的圆心叫三角形的内心
②三角形的内心到三边的距离相等
①三角形的内心是三角形角平分线的交点
③三角形的内心一定在三角形的内部
三角形内心的性质
名称
确定方法
图形
性质
(三角形内切圆的圆心)
三角形三边中垂线的交点
三角形三条
角平分线的
交点
(2)外心不一定在三角形的内部.
(3)内心在三角形内部.
(三角形
外接圆的
圆心)
外 心
内 心
(1)OA=OB=OC
(1)到三边的距离相等;
(2)OA、OB、OC
分别平分∠BAC、
∠ABC、∠ACB;
例2 如图,在△ABC中,点O是内心, (1)若∠ABC=50°, ∠ACB=70°,求∠BOC的度数
A
B
C
O
(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
20
130
∠OCB=
1
2
∠ACB=35 °
解(1)∵点O是△ABC的内心,
∠ABC= 25 °
∴ ∠OBC=
1
2
试探讨∠BOC与∠A之间存在怎样的数量关系?
∴ ∠BOC=180°-(∠OBC+ ∠OCB)
= 180 °-60 °=120 °
=180°-(25°+ 35°)
a
b
c
r
r
r
已知△ABC的三边BC,AB,AC分别为
a, b, c, I为内心,内切圆半径为r
求△ABC的面积
A
B
C
I
S△ABC =S△ABI + S△BCI + S△ACI
=
a·r
2
+
b·r
2
+
c·r
2
=
练习:边长为3,4,5的三角形的内切圆半径是__
1
证明:连结AI,BI,CI
(a+b+c)·r
2
例3
课堂小结:
1、本节课从实际问题入手,探索得出三角形内切圆的作法 .。
2、通过类比三角形的外接圆与圆的内接三角形概念得出
三角形的内切圆、圆的外切三角形概念。
3、学习时要明确“接”和“切”的含义、弄清“内心”与
“外心”的区别。
作业:
1.课本80页A组第5题
2.已知⊙O为RtΔABC的内切圆,且∠C=90°, AB=5,AC=3,求∠ BOA的度数和内切圆⊙O的半径。
三角形的内切圆
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
A
B
C
三角形的内切圆
A
B
C
和三角形各边都相切的圆叫三角形的内切圆
三角形叫圆的外切三角形
问题1:作圆的关键是什么?
问题2:怎样确定圆心的位置?
问题3:圆心的位置确定后怎样确定圆的半径?
A
B
C
(确定圆心和半径)
(作两条角平分线,其交点就是圆心的位置)
(过圆心作三角形一边的垂线,垂线段的长就是圆的半径)
例1
已知: △ABC(如图)
求作:△ABC的内切圆
问题4:在这块三角形材料上还能裁下更大的圆吗
(不能)任何一个三角形都有且只有一个内切圆
而任意一个圆有无数个外切三角形
3、以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆.
例1
已知: △ABC(如图)
求作:△ABC的内切圆
A
B
C
M
N
I
D
作法:1、作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
三角形内切圆的圆心叫三角形的内心
②三角形的内心到三边的距离相等
①三角形的内心是三角形角平分线的交点
③三角形的内心一定在三角形的内部
三角形内心的性质
名称
确定方法
图形
性质
(三角形内切圆的圆心)
三角形三边中垂线的交点
三角形三条
角平分线的
交点
(2)外心不一定在三角形的内部.
(3)内心在三角形内部.
(三角形
外接圆的
圆心)
外 心
内 心
(1)OA=OB=OC
(1)到三边的距离相等;
(2)OA、OB、OC
分别平分∠BAC、
∠ABC、∠ACB;
例2 如图,在△ABC中,点O是内心, (1)若∠ABC=50°, ∠ACB=70°,求∠BOC的度数
A
B
C
O
(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
20
130
∠OCB=
1
2
∠ACB=35 °
解(1)∵点O是△ABC的内心,
∠ABC= 25 °
∴ ∠OBC=
1
2
试探讨∠BOC与∠A之间存在怎样的数量关系?
∴ ∠BOC=180°-(∠OBC+ ∠OCB)
= 180 °-60 °=120 °
=180°-(25°+ 35°)
a
b
c
r
r
r
已知△ABC的三边BC,AB,AC分别为
a, b, c, I为内心,内切圆半径为r
求△ABC的面积
A
B
C
I
S△ABC =S△ABI + S△BCI + S△ACI
=
a·r
2
+
b·r
2
+
c·r
2
=
练习:边长为3,4,5的三角形的内切圆半径是__
1
证明:连结AI,BI,CI
(a+b+c)·r
2
例3
课堂小结:
1、本节课从实际问题入手,探索得出三角形内切圆的作法 .。
2、通过类比三角形的外接圆与圆的内接三角形概念得出
三角形的内切圆、圆的外切三角形概念。
3、学习时要明确“接”和“切”的含义、弄清“内心”与
“外心”的区别。
作业:
1.课本80页A组第5题
2.已知⊙O为RtΔABC的内切圆,且∠C=90°, AB=5,AC=3,求∠ BOA的度数和内切圆⊙O的半径。
