高中数学湘教版选修2-2:(课件)5.3 复数的四则运算
文档属性
| 名称 | 高中数学湘教版选修2-2:(课件)5.3 复数的四则运算 |  | |
| 格式 | zip | ||
| 文件大小 | 577.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-14 21:18:24 | ||
图片预览







文档简介
(共26张PPT)
5.3 复数的四则运算
5.3
课堂互动讲练
知能优化训练
课前自主学案
学习目标
学习目标
1.掌握复数代数形式的加、减、乘除运算法则.
2.能正确进行复数代数形式的四则运算.
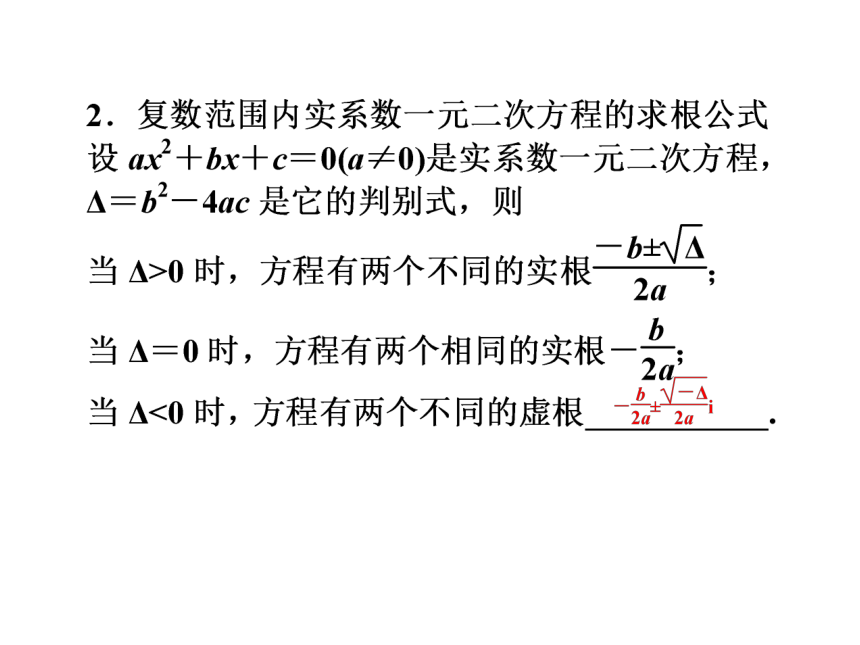
3.掌握复数范围内一元二次方程的求根公式,并会在复数范围内解一元二次方程.
课前自主学案
温故夯基
-1
必要不充分
充要
正数
0
知新益能
(a-c)+(b-d)i
(ac-bd)+(ad+bc)i
(a+c)+(b+d)i
思考感悟
怎样理解复数的乘、除法运算法则的合理性?
提示:复数代数形式的乘法运算法则是一种规定.除法是乘法的逆运算.其合理性,可以从以下几点理解:
(1)当复数的虚部为零时,与实数的乘法法则一致.
(2)实数乘法的交换律、结合律及乘法对加法的分配律在复数集中仍然成立.
(3)两个复数的积(商)仍是唯一确定的复数.
(4)可以推广到多个复数进行乘、除法运算.
课堂互动讲练
复数的加减乘除运算
考点突破
(1)类比实数的加减运算,若有括号,先计算括号内的;若没有括号,可从左到右依次进行.
(2)复数的乘法可以按照乘法法则进行,对于能够使用乘法公式计算的两个复数的乘法,用乘法公式更简便,例如平方差公式,完全平方公式等.
例1
【思路点拨】 按复数的四则运算法则计算,注意最后结果写成a+bi(a,b∈R)的形式.
【解】 (1)(1+2i)+(3-4i)-(5+6i)
=(4-2i)-(5+6i)=-1-8i.
(2)5i-[(3+4i)-(-1+3i)]=5i-(4+i)=-4+4i.
(3)(a+bi)-(2a-3bi)-3i
=(a-2a)+[b-(-3b)-3]i=-a+(4b-3)i.
(4)(1-i)(1+i)+(-1+i)=1-i2-1+i
=1+i.
【名师点评】 (1)复数的四则运算的结果仍是一个复数;
(2)复数的加、减、乘运算,只需把“i”看作一个字母,按照多项式的加、减、乘运算进行.
(3)复数除法的实质是分母实数化.
(4)对于复数的混合运算,仍可按照先乘方、再乘除、后加减的顺序,有括号先计算括号内的.
在复数范围内解方程
实系数一元二次方程,可直接利用求根公式解,复系数方程利用复数相等求解.
例2
【思路点拨】 系数为常数的直接利用求根公式,系数含字母的分类讨论求解.
【名师点评】 解一元二次方程必须注意两点:(1)二次项系数是否为零;(2)Δ是大于、等于零还是小于零.
自我挑战2 求实数k,使方程x2+(k+2i)x+2+ki=0至少有一个实根.
复数的乘方运算
例3
【思路点拨】 根据复数乘方的运算性质,将高次运算化为低次运算处理.
【名师点评】 复数的运算顺序与实数的运算顺序相同,是先进行高级运算(乘方、开方),再进行次级运算(乘、除),最后进行低级运算(加、减),如有i的幂运算,先利用i的幂的周期性,将其次数降低,然后再进行四则运算.
方法感悟
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
5.3 复数的四则运算
5.3
课堂互动讲练
知能优化训练
课前自主学案
学习目标
学习目标
1.掌握复数代数形式的加、减、乘除运算法则.
2.能正确进行复数代数形式的四则运算.
3.掌握复数范围内一元二次方程的求根公式,并会在复数范围内解一元二次方程.
课前自主学案
温故夯基
-1
必要不充分
充要
正数
0
知新益能
(a-c)+(b-d)i
(ac-bd)+(ad+bc)i
(a+c)+(b+d)i
思考感悟
怎样理解复数的乘、除法运算法则的合理性?
提示:复数代数形式的乘法运算法则是一种规定.除法是乘法的逆运算.其合理性,可以从以下几点理解:
(1)当复数的虚部为零时,与实数的乘法法则一致.
(2)实数乘法的交换律、结合律及乘法对加法的分配律在复数集中仍然成立.
(3)两个复数的积(商)仍是唯一确定的复数.
(4)可以推广到多个复数进行乘、除法运算.
课堂互动讲练
复数的加减乘除运算
考点突破
(1)类比实数的加减运算,若有括号,先计算括号内的;若没有括号,可从左到右依次进行.
(2)复数的乘法可以按照乘法法则进行,对于能够使用乘法公式计算的两个复数的乘法,用乘法公式更简便,例如平方差公式,完全平方公式等.
例1
【思路点拨】 按复数的四则运算法则计算,注意最后结果写成a+bi(a,b∈R)的形式.
【解】 (1)(1+2i)+(3-4i)-(5+6i)
=(4-2i)-(5+6i)=-1-8i.
(2)5i-[(3+4i)-(-1+3i)]=5i-(4+i)=-4+4i.
(3)(a+bi)-(2a-3bi)-3i
=(a-2a)+[b-(-3b)-3]i=-a+(4b-3)i.
(4)(1-i)(1+i)+(-1+i)=1-i2-1+i
=1+i.
【名师点评】 (1)复数的四则运算的结果仍是一个复数;
(2)复数的加、减、乘运算,只需把“i”看作一个字母,按照多项式的加、减、乘运算进行.
(3)复数除法的实质是分母实数化.
(4)对于复数的混合运算,仍可按照先乘方、再乘除、后加减的顺序,有括号先计算括号内的.
在复数范围内解方程
实系数一元二次方程,可直接利用求根公式解,复系数方程利用复数相等求解.
例2
【思路点拨】 系数为常数的直接利用求根公式,系数含字母的分类讨论求解.
【名师点评】 解一元二次方程必须注意两点:(1)二次项系数是否为零;(2)Δ是大于、等于零还是小于零.
自我挑战2 求实数k,使方程x2+(k+2i)x+2+ki=0至少有一个实根.
复数的乘方运算
例3
【思路点拨】 根据复数乘方的运算性质,将高次运算化为低次运算处理.
【名师点评】 复数的运算顺序与实数的运算顺序相同,是先进行高级运算(乘方、开方),再进行次级运算(乘、除),最后进行低级运算(加、减),如有i的幂运算,先利用i的幂的周期性,将其次数降低,然后再进行四则运算.
方法感悟
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
同课章节目录
