3.2立体几何中的向量方法-人教A版高中数学选修2-1课时练习(Word含答案)
文档属性
| 名称 | 3.2立体几何中的向量方法-人教A版高中数学选修2-1课时练习(Word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 227.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-25 13:30:31 | ||
图片预览

文档简介
高二年级(数学)学科习题卷
立体几何中的向量方法
选择题:
1.如图1,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,
点E是AB上一点,当二面角P-EC-D为时,AE等于( )
A.1 B. C.2- D.2-
图(1) 图(2)
2.如图2,四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为,则直线BE与平面ACD所成角的正弦值为( )
A. B. C. D.
3.在直三棱柱中,底面是等腰直角三角形,,侧棱,D,E分别是与的中点,点E在平面ABD上的射影是的重心G.则与平面所成角的余弦值( )
A. B. C. D.
4.在棱长为的正方体中,则平面与平面间的距离 ( )
A. B. C . D.
二、填空题:
5.已知在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点,则直线AE与平面A1ED1所成角的大小为 .?
6.正方体ABCD-A1B1C1D1中,面ABD1与面B1BD1所成角的大小为_________________.
7.已知正方体的棱长为,求平面与平面之间的距离________________.
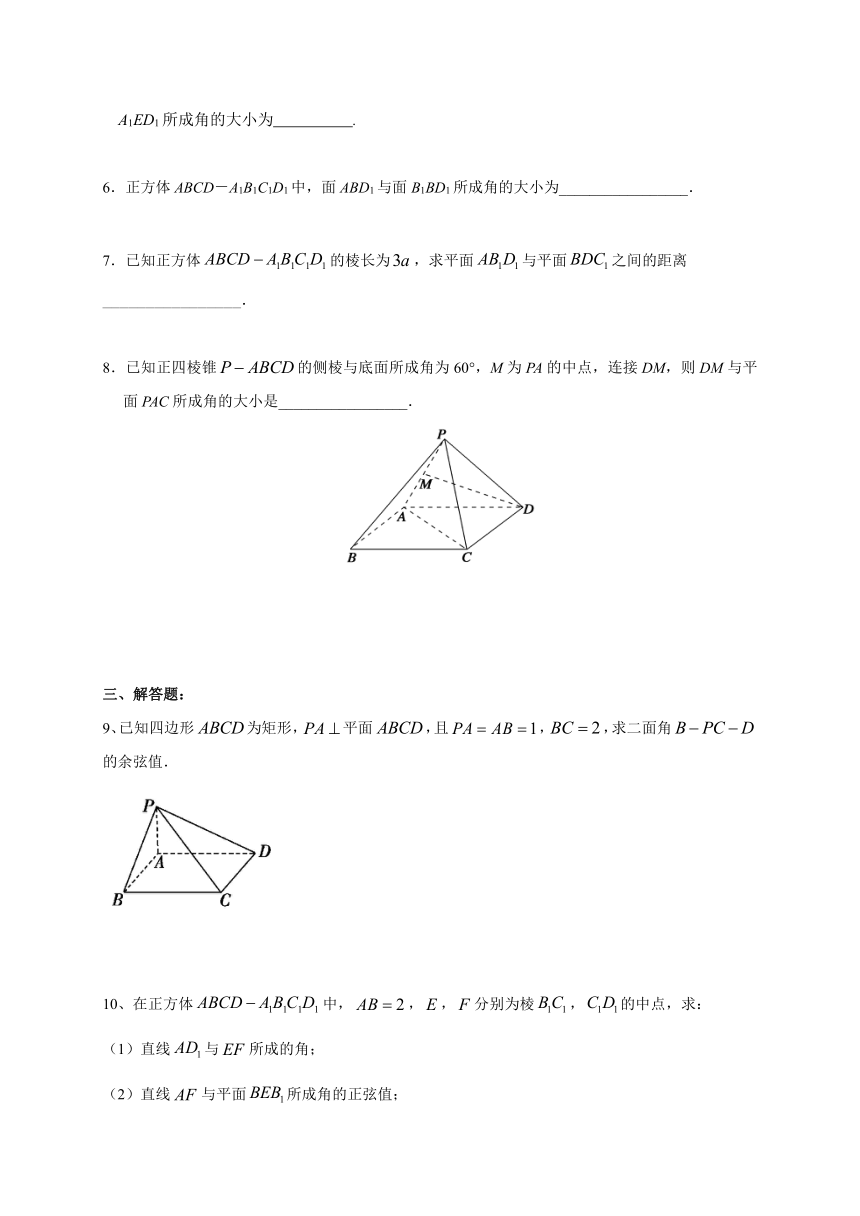
8.已知正四棱锥的侧棱与底面所成角为60°,M为PA的中点,连接DM,则DM与平面PAC所成角的大小是_________________.
三、解答题:
9、已知四边形为矩形,平面,且,,求二面角的余弦值.
10、在正方体中,,,分别为棱,的中点,求:
(1)直线与所成的角;
(2)直线与平面所成角的正弦值;
(3)二面角的余弦值.
11、如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上异于A、B的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角的余弦值.
12、如图,直三棱柱中,△ABC是等边三角形,D是BC的中点.
(1)求证:A1B∥平面ADC1;
(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值.
答案解析:
选择题:1-4DCBB
填空题:5.90°
6.60°
7.根号3a/3
8.45°
9.5/13
10.(1)60。(2)2根号2/3(3)0
11.(1) 因为PA⊥圆所在的平面ABC,BC?平面ABC,所以可得PA⊥BC,
因为C是圆O上的点,AB是圆O的直径,所以由直径对的圆周角等于90°,可得BC⊥AC.再由AC∩PA=A,利用直线和平面垂直的判定定理可得BC⊥平面PAC所以面面垂直
(2)根号6/4
12.(1)略(2)2根号35/35
立体几何中的向量方法
选择题:
1.如图1,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,
点E是AB上一点,当二面角P-EC-D为时,AE等于( )
A.1 B. C.2- D.2-
图(1) 图(2)
2.如图2,四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为,则直线BE与平面ACD所成角的正弦值为( )
A. B. C. D.
3.在直三棱柱中,底面是等腰直角三角形,,侧棱,D,E分别是与的中点,点E在平面ABD上的射影是的重心G.则与平面所成角的余弦值( )
A. B. C. D.
4.在棱长为的正方体中,则平面与平面间的距离 ( )
A. B. C . D.
二、填空题:
5.已知在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点,则直线AE与平面A1ED1所成角的大小为 .?
6.正方体ABCD-A1B1C1D1中,面ABD1与面B1BD1所成角的大小为_________________.
7.已知正方体的棱长为,求平面与平面之间的距离________________.
8.已知正四棱锥的侧棱与底面所成角为60°,M为PA的中点,连接DM,则DM与平面PAC所成角的大小是_________________.
三、解答题:
9、已知四边形为矩形,平面,且,,求二面角的余弦值.
10、在正方体中,,,分别为棱,的中点,求:
(1)直线与所成的角;
(2)直线与平面所成角的正弦值;
(3)二面角的余弦值.
11、如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上异于A、B的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角的余弦值.
12、如图,直三棱柱中,△ABC是等边三角形,D是BC的中点.
(1)求证:A1B∥平面ADC1;
(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值.
答案解析:
选择题:1-4DCBB
填空题:5.90°
6.60°
7.根号3a/3
8.45°
9.5/13
10.(1)60。(2)2根号2/3(3)0
11.(1) 因为PA⊥圆所在的平面ABC,BC?平面ABC,所以可得PA⊥BC,
因为C是圆O上的点,AB是圆O的直径,所以由直径对的圆周角等于90°,可得BC⊥AC.再由AC∩PA=A,利用直线和平面垂直的判定定理可得BC⊥平面PAC所以面面垂直
(2)根号6/4
12.(1)略(2)2根号35/35
