第一章 丰富的图形世界检测题(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
《第一章 丰富的图形世界》检测题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共36分)
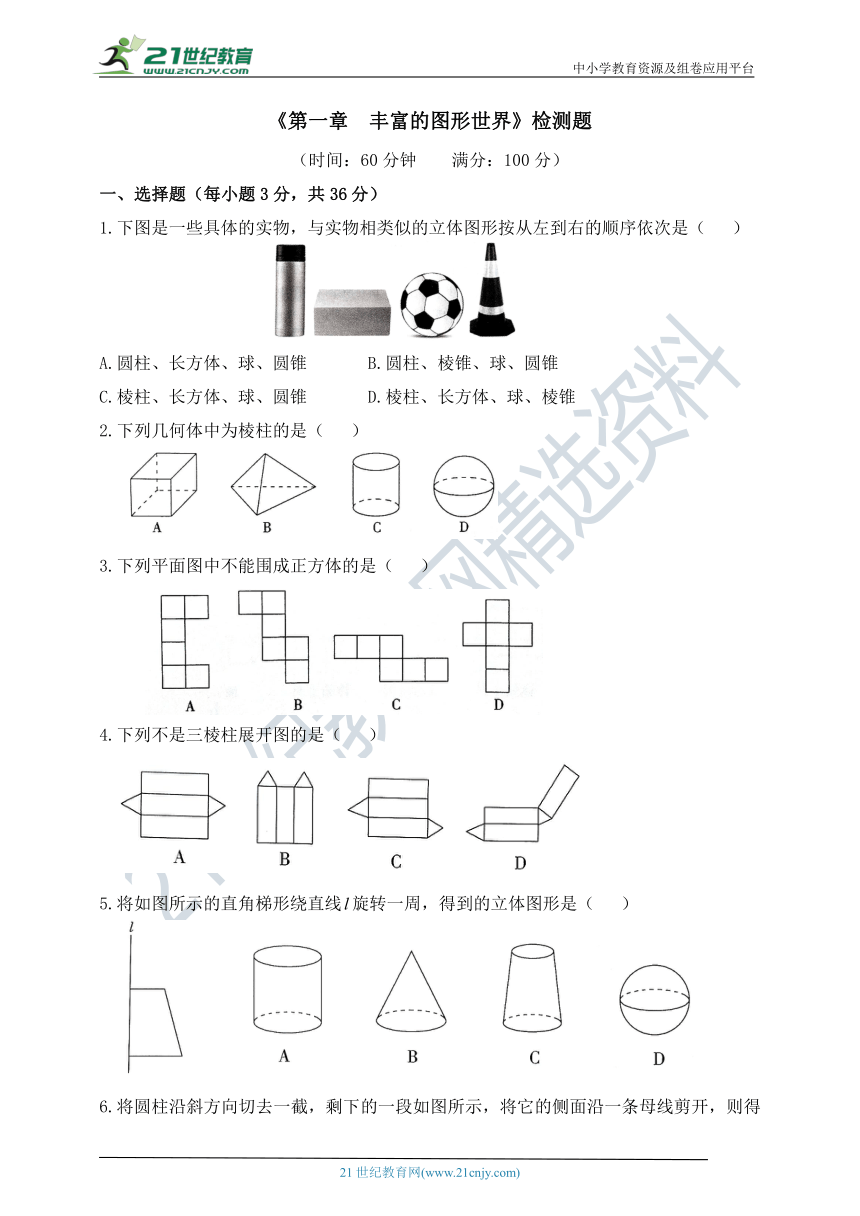
1.下图是一些具体的实物,与实物相类似的立体图形按从左到右的顺序依次是( )
A.圆柱、长方体、球、圆锥 B.圆柱、棱锥、球、圆锥
C.棱柱、长方体、球、圆锥 D.棱柱、长方体、球、棱锥
2.下列几何体中为棱柱的是( )
3.下列平面图中不能围成正方体的是( )
4.下列不是三棱柱展开图的是( )
5.将如图所示的直角梯形绕直线旋转一周,得到的立体图形是( )
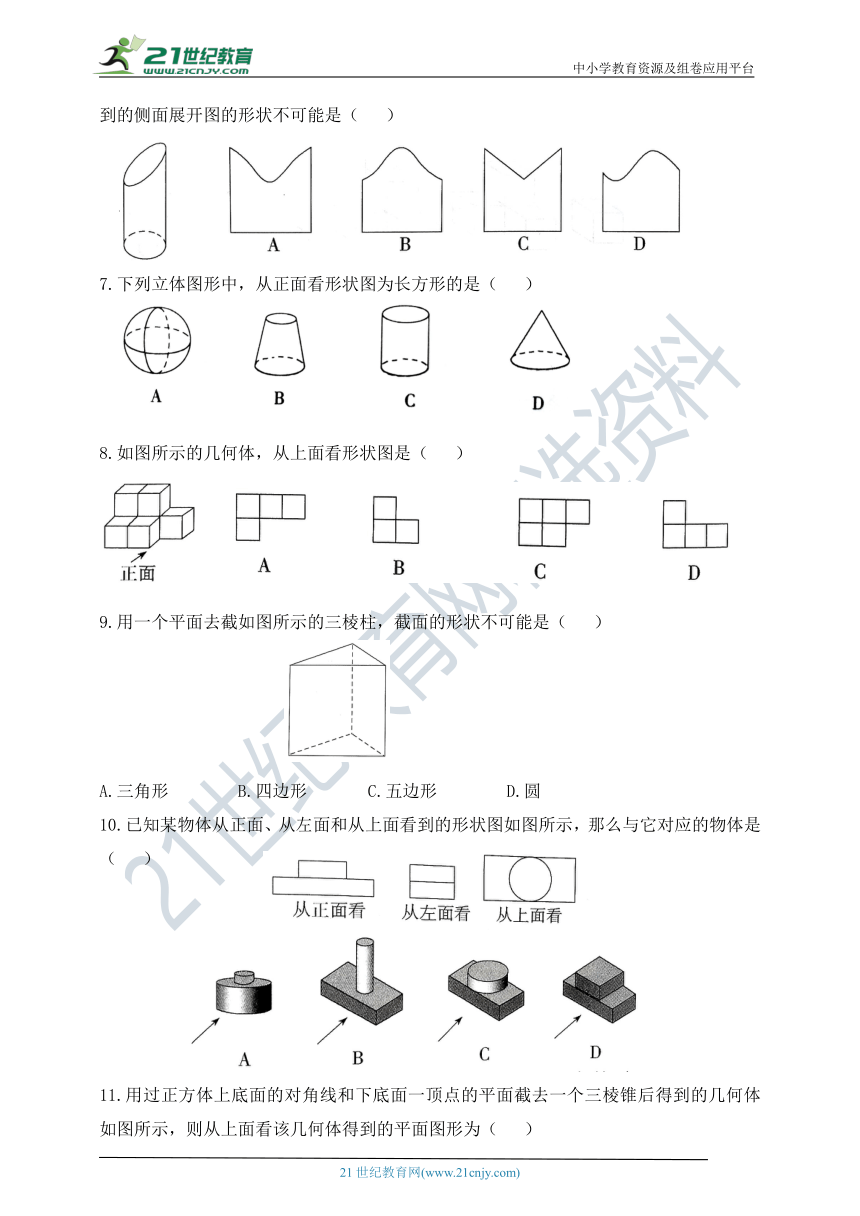
6.将圆柱沿斜方向切去一截,剩下的一段如图所示,将它的侧面沿一条母线剪开,则得到的侧面展开图的形状不可能是( )
7.下列立体图形中,从正面看形状图为长方形的是( )
8.如图所示的几何体,从上面看形状图是( )
9.用一个平面去截如图所示的三棱柱,截面的形状不可能是( )
A.三角形 B.四边形 C.五边形 D.圆
10.已知某物体从正面、从左面和从上面看到的形状图如图所示,那么与它对应的物体是( )
11.用过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥后得到的几何体如图所示,则从上面看该几何体得到的平面图形为( )
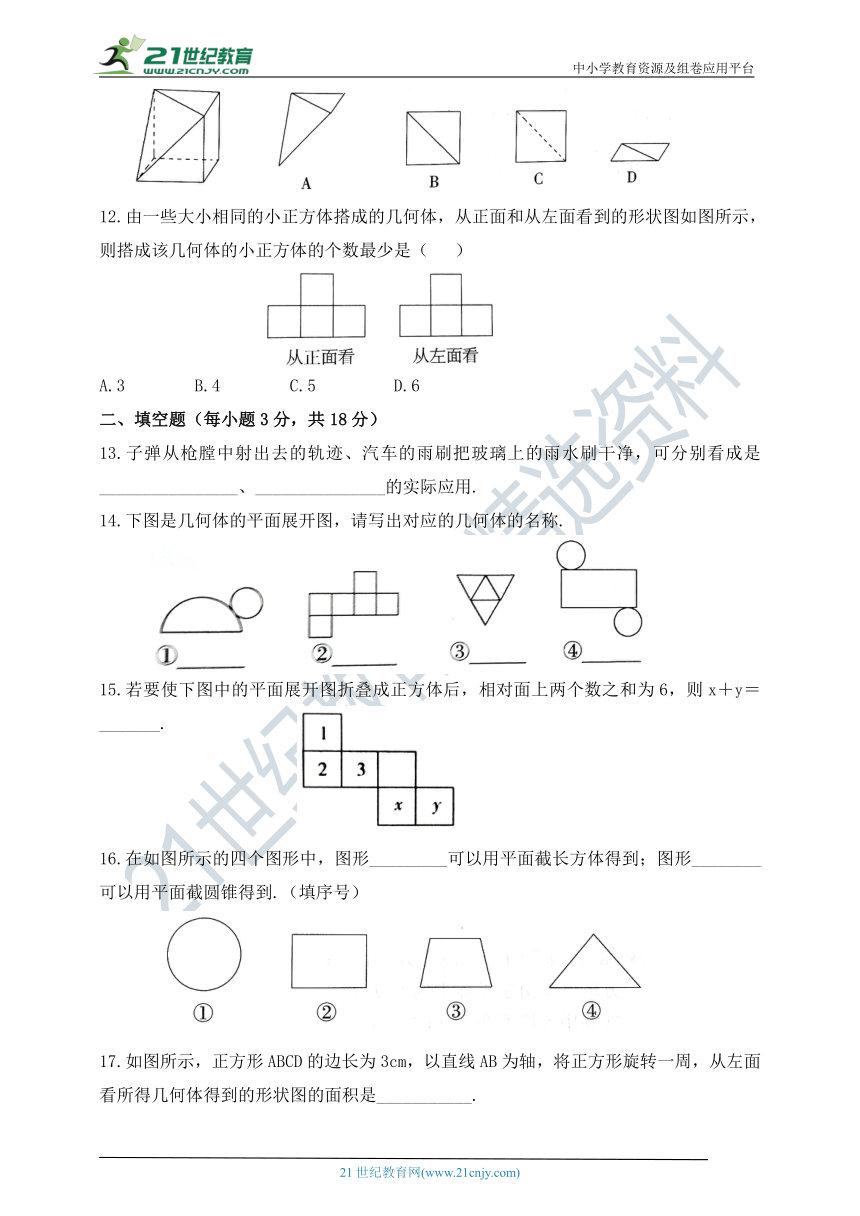
12.由一些大小相同的小正方体搭成的几何体,从正面和从左面看到的形状图如图所示,则搭成该几何体的小正方体的个数最少是( )
A.3 B.4 C.5 D.6
二、填空题(每小题3分,共18分)
13.子弹从枪膛中射出去的轨迹、汽车的雨刷把玻璃上的雨水刷干净,可分别看成是________________、_______________的实际应用.
14.下图是几何体的平面展开图,请写出对应的几何体的名称.
15.若要使下图中的平面展开图折叠成正方体后,相对面上两个数之和为6,则x+y=_______.
16.在如图所示的四个图形中,图形_________可以用平面截长方体得到;图形________可以用平面截圆锥得到.(填序号)
17.如图所示,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,从左面看所得几何体得到的形状图的面积是___________.
18.下图是从正面和从左面看由若干个正方体搭建而成的几何体得到的形状图,那么下列图形中可以作为从上面看该几何体得到的形状图的序号是__________.
三、解答题(共46分)
19.(7分)如图所示,一个正方体钢块的正中央被挖去了一个正方形孔,请画出从正面,从左面和从上面看到的此正方体钢块的形状图.
20.(7分)一个直棱柱有18个面,且所有的侧棱长的和为64,底面边长都是3.
(1)这是几棱柱?
(2)求此棱柱的侧面展开图的面积.
21.(8分)如图所示,用1、2、3、4标出的4块正方形以及由字母标出的八块正方形中的任意一块,共要用5块连在一起的正方形折成一个无盖方盒,共有几种不同的方法?
22.(8分)下图是一个物体从正面、左面、上面看到的形状图,试回答下列问题:
(1)该物体有几层高?
(2)该物体的最高部分位于哪里?
23.(8分)探究:有一长6cm,宽4cm的长方形纸板,要求以其一组对边中点所在直线为轴旋转180°、得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转如图7①;
方案二:以较短的一组对边中点所在直线为轴旋转如图②.
(1)请通过计算说明哪种方法得到的圆柱的体积大;
(2)如果该长方形纸板的长、宽分别是5cm和3cm呢?请通过计算说明哪种方法得到的圆柱的体积大;
(3)通过以上探究,你发现对于同一个长方形(不包括正方形),以其一组对边中点所在直线为轴旋转一周得到一个圆柱,怎样操作所得到的圆柱的体积较大(不必说明原因)?
24.(8分)图①②③均是由棱长为1的小立方块摆放而成的几何体,按照这样的方法继续摆放,自上而下分别叫做第一层、第二层、…第n层,当摆放至第n层时,构成这个几何体的小立方块的总个数记为kn,它的表面积记为Sn.试求:
(1)k2和S2;
(2)k3和S3;
(3)k10和S10.
参考答案
一、选择题
1.A 2.A 3.A 4.B 5.C 6.C 7.C 8.C 9.D 10.C 11.B 12.B
二、填空题
13.点动成线;线动成面 14.圆锥;正方体;三棱锥;圆柱 15. 8
16. ②③④;①④ 17. 18cm2 18. ①②③
三、解答题
19. 如图所示.
20.(1)十六棱柱.
(2)由题意得,侧棱长为64÷16=4,直棱柱的侧面展开图为长方形,面积为3×16×4=192,即此棱柱的侧面展开图的面积为192.
21. 将4个数字和1个字母括起来的不同的方法有:
(1、2、3、4、A);(1、2、3、4、B);(1、2、3、4、C);(1、2、3、4、D);(1、2、3、4、E);(1、2、3、4、G),共有6种不同的方法.
22. (1)根据从正面看到的形状图可得该物体有2层高.
(2)如图所示,该物体的最高部分位于阴影部分.
23.(1)方案一:π×32×4=36π(cm3),
方案二:π×22×6=24π(cm3),
∵36π>24π,∴方案一得到的圆柱的体积大.
(2)方案一:π××3=(cm3),
方案二:π××5=(cm3),
∵>,∴方案一得到的圆柱的体积大.
(3)由(1)(2)得,以较长一组对边中点所在直线为轴旋转一周得到的圆柱的体积大.
24.解析(1)k2=1+3=4,S2=(1+2)×6=18.
(2)k3=1+3+6=10,S3=(1+2+3)×6=36.
(3)k10=1+3+6+10+15+21+28+36+4+55=220,S10=(1+2+3+…+10)×6=330.
_21?????????è?????(www.21cnjy.com)_
《第一章 丰富的图形世界》检测题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共36分)
1.下图是一些具体的实物,与实物相类似的立体图形按从左到右的顺序依次是( )
A.圆柱、长方体、球、圆锥 B.圆柱、棱锥、球、圆锥
C.棱柱、长方体、球、圆锥 D.棱柱、长方体、球、棱锥
2.下列几何体中为棱柱的是( )
3.下列平面图中不能围成正方体的是( )
4.下列不是三棱柱展开图的是( )
5.将如图所示的直角梯形绕直线旋转一周,得到的立体图形是( )
6.将圆柱沿斜方向切去一截,剩下的一段如图所示,将它的侧面沿一条母线剪开,则得到的侧面展开图的形状不可能是( )
7.下列立体图形中,从正面看形状图为长方形的是( )
8.如图所示的几何体,从上面看形状图是( )
9.用一个平面去截如图所示的三棱柱,截面的形状不可能是( )
A.三角形 B.四边形 C.五边形 D.圆
10.已知某物体从正面、从左面和从上面看到的形状图如图所示,那么与它对应的物体是( )
11.用过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥后得到的几何体如图所示,则从上面看该几何体得到的平面图形为( )
12.由一些大小相同的小正方体搭成的几何体,从正面和从左面看到的形状图如图所示,则搭成该几何体的小正方体的个数最少是( )
A.3 B.4 C.5 D.6
二、填空题(每小题3分,共18分)
13.子弹从枪膛中射出去的轨迹、汽车的雨刷把玻璃上的雨水刷干净,可分别看成是________________、_______________的实际应用.
14.下图是几何体的平面展开图,请写出对应的几何体的名称.
15.若要使下图中的平面展开图折叠成正方体后,相对面上两个数之和为6,则x+y=_______.
16.在如图所示的四个图形中,图形_________可以用平面截长方体得到;图形________可以用平面截圆锥得到.(填序号)
17.如图所示,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,从左面看所得几何体得到的形状图的面积是___________.
18.下图是从正面和从左面看由若干个正方体搭建而成的几何体得到的形状图,那么下列图形中可以作为从上面看该几何体得到的形状图的序号是__________.
三、解答题(共46分)
19.(7分)如图所示,一个正方体钢块的正中央被挖去了一个正方形孔,请画出从正面,从左面和从上面看到的此正方体钢块的形状图.
20.(7分)一个直棱柱有18个面,且所有的侧棱长的和为64,底面边长都是3.
(1)这是几棱柱?
(2)求此棱柱的侧面展开图的面积.
21.(8分)如图所示,用1、2、3、4标出的4块正方形以及由字母标出的八块正方形中的任意一块,共要用5块连在一起的正方形折成一个无盖方盒,共有几种不同的方法?
22.(8分)下图是一个物体从正面、左面、上面看到的形状图,试回答下列问题:
(1)该物体有几层高?
(2)该物体的最高部分位于哪里?
23.(8分)探究:有一长6cm,宽4cm的长方形纸板,要求以其一组对边中点所在直线为轴旋转180°、得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转如图7①;
方案二:以较短的一组对边中点所在直线为轴旋转如图②.
(1)请通过计算说明哪种方法得到的圆柱的体积大;
(2)如果该长方形纸板的长、宽分别是5cm和3cm呢?请通过计算说明哪种方法得到的圆柱的体积大;
(3)通过以上探究,你发现对于同一个长方形(不包括正方形),以其一组对边中点所在直线为轴旋转一周得到一个圆柱,怎样操作所得到的圆柱的体积较大(不必说明原因)?
24.(8分)图①②③均是由棱长为1的小立方块摆放而成的几何体,按照这样的方法继续摆放,自上而下分别叫做第一层、第二层、…第n层,当摆放至第n层时,构成这个几何体的小立方块的总个数记为kn,它的表面积记为Sn.试求:
(1)k2和S2;
(2)k3和S3;
(3)k10和S10.
参考答案
一、选择题
1.A 2.A 3.A 4.B 5.C 6.C 7.C 8.C 9.D 10.C 11.B 12.B
二、填空题
13.点动成线;线动成面 14.圆锥;正方体;三棱锥;圆柱 15. 8
16. ②③④;①④ 17. 18cm2 18. ①②③
三、解答题
19. 如图所示.
20.(1)十六棱柱.
(2)由题意得,侧棱长为64÷16=4,直棱柱的侧面展开图为长方形,面积为3×16×4=192,即此棱柱的侧面展开图的面积为192.
21. 将4个数字和1个字母括起来的不同的方法有:
(1、2、3、4、A);(1、2、3、4、B);(1、2、3、4、C);(1、2、3、4、D);(1、2、3、4、E);(1、2、3、4、G),共有6种不同的方法.
22. (1)根据从正面看到的形状图可得该物体有2层高.
(2)如图所示,该物体的最高部分位于阴影部分.
23.(1)方案一:π×32×4=36π(cm3),
方案二:π×22×6=24π(cm3),
∵36π>24π,∴方案一得到的圆柱的体积大.
(2)方案一:π××3=(cm3),
方案二:π××5=(cm3),
∵>,∴方案一得到的圆柱的体积大.
(3)由(1)(2)得,以较长一组对边中点所在直线为轴旋转一周得到的圆柱的体积大.
24.解析(1)k2=1+3=4,S2=(1+2)×6=18.
(2)k3=1+3+6=10,S3=(1+2+3)×6=36.
(3)k10=1+3+6+10+15+21+28+36+4+55=220,S10=(1+2+3+…+10)×6=330.
_21?????????è?????(www.21cnjy.com)_
