高中数学湘教版选修2-1:(课件)2.3 抛物线 2.3.1 抛物线的定义与标准方程
文档属性
| 名称 | 高中数学湘教版选修2-1:(课件)2.3 抛物线 2.3.1 抛物线的定义与标准方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 812.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-14 22:24:00 | ||
图片预览








文档简介
(共33张PPT)
2.3 抛物线
2.3.1 抛物线的定义与标准方程
2.3.1
课堂互动讲练
知能优化训练
课前自主学案
学习目标
学习目标
1.掌握抛物线的定义及焦点、准线的概念.
2.会求简单的抛物线的方程.
课前自主学案
温故夯基
抛物线.
2
知新益能
相等
准线.
思考感悟
1.如何理解抛物线的定义?
提示:(1)抛物线定义的实质可归结为“一动三定”,一个动点,设为M;一个定点F即抛物线的焦点;一条定直线l即抛物线的准线;一个定值即点M与点F的距离和它到直线l的距离之比等于1.
(2)在抛物线的定义中,定点F不能在直线l上,否则,动点M的轨迹就不是抛物线,而是过点F垂直于直线l的一条直线.如到点F(1,0)与到直线l:x+y-1=0的距离相等的点的轨迹方程为x-y-1=0,轨迹为过点F且与直线l垂直的一条直线.
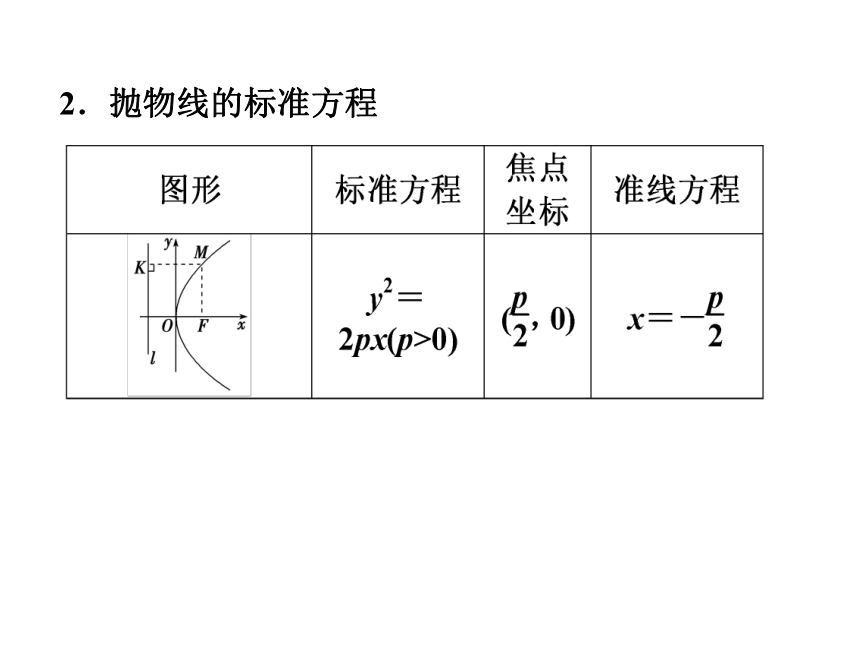
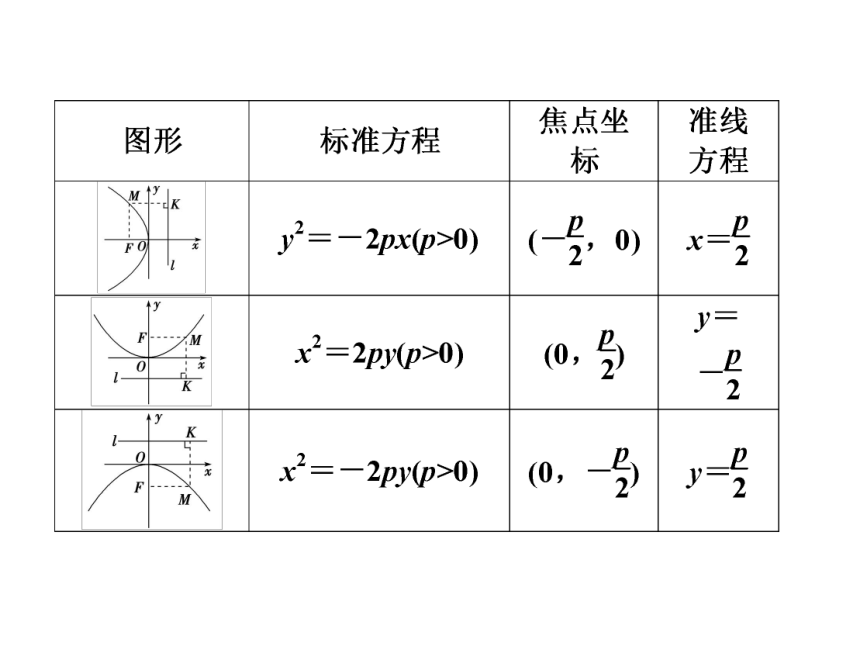
2.抛物线的标准方程
思考感悟
2.如何确定抛物线的焦点位置和开口方向?
提示:一次项变量为x(或y),则焦点在x轴(或y轴)上;若系数为正,则焦点在正半轴上;系数为负,则焦点在负半轴上,焦点确定,开口方向也随之确定.
四种位置的抛物线标准方程的对比:
(1)共同点:
①原点在抛物线上;②焦点在坐标轴上;
③焦点的非零坐标都是一次项系数的.
(2)不同点:
①焦点在x轴上时,方程的右端为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2;②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)负半轴上,方程右端取负号.
课堂互动讲练
确定抛物线的焦点、开口方向、准线方程
考点突破
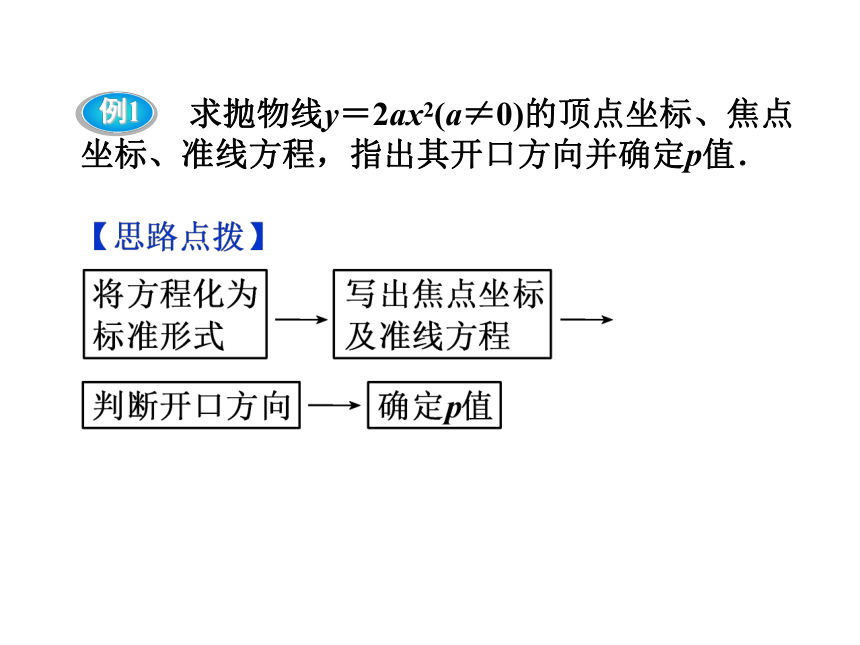
例1
求抛物线y=2ax2(a≠0)的顶点坐标、焦点坐标、准线方程,指出其开口方向并确定p值.
自我挑战1 已知抛物线的标准方程如下,分别求其焦点坐标和准线方程.
(1)y2=6x;(2)2y2+5x=0.
求抛物线的标准方程
求抛物线的方程通常有定义法和待定系数法.由于标准方程有四种形式,因而在求方程时应首先确定焦点在哪一个半轴上,进而确定方程的形式,然后再利用已知条件确定p的值.
例2
求满足下列条件的抛物线的标准方程:
(1)过点(-3,2);
(2)焦点在直线x-2y-4=0上.
【思路点拨】 首先判断焦点可能存在的位置,设出适当的方程的形式,然后求出参数p即可.
【名师点评】 (1)确定抛物线的标准方程,从形式上看,只需求一个参数p,但由于标准方程有四种类型,因此,还应确定开口方向,当开口方向不确定时,应进行分类讨论.有时也可设标准方程的统一形式,避免讨论,如焦点在x轴上的抛物线标准方程可设为y2=2mx(m≠0),焦点在y轴上的抛物线标准方程可设为x2=2my(m≠0).
(2)求抛物线标准方程的方法:
特别注意在设标准方程时,若焦点位置不确定,要分类讨论.
抛物线的定义及其应用
对于抛物线中的最值问题,其求解方法为把到焦点的距离化为到准线的距离,到准线的距离化为到焦点的距离.
例3
【思路点拨】 先根据抛物线的定义求出抛物线方程.再利用平面几何的有关性质求出最小值.
【解】 (1)点M到点F(0,1)的距离比它到x轴的距离大1,即“点M到点F(0,1)的距离等于它到直线y=-1的距离”,所以点M的轨迹是以F为焦点,直线y=-1为准线的抛物线,此时,p=2,
故所求抛物线方程G为x2=4y.
(2011年青州高二检测)已知点A(12,6),点M到F(0,1)的距离比它到x轴的距离大1.
(1)求点M的轨迹方程G;
(2)在G上是否存在一点P,使点P到点A的距离与点P到x轴的距离之和取得最小值?若存在,求此时点P的坐标;若不存在,请说明理由.
【名师点评】 根据抛物线的定义,平面内与一个定点F和一条不过该点的直线l的距离相等的点的集合叫作抛物线,另一方面,抛物线上的任意一点到焦点的距离等于该点到准线的距离.就是说,定义具有判定和性质的双重作用,本题利用抛物线的定义求出点的轨迹方程,又利用抛物线的定义,“化曲折为平直”,将两点间的距离的和转化为点到直线的距离求得最小值,这是平面几何性质的典型运用.
自我挑战3 已知抛物线y2=4x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出取最小值时P点坐标.
解:
方法感悟
1.(1)“p”是抛物线的焦点到准线的距离,所以p的值永远大于0.特别注意,当抛物线标准方程的一次项系数为负时,不要出现错误.
(2)只有顶点在坐标原点,焦点在坐标轴上的抛物线方程才有标准形式.
(3)抛物线的开口方向取决于一次项变量(x或y)的取值范围.如抛物线x2=-2y,一次项变量y≤0,所以抛物线开口向下.
2.标准方程中只有一个参数p,求抛物线的标准方程,只需求出p的值即可,常用待定系数法.
(1)用待定系数法求抛物线标准方程时,一定先确定焦点位置与开口方向,如果开口方向不确定时,可设所求抛物线方程为y2=ax(a≠0),或者x2=ay(a≠0);
(2)当抛物线不在标准位置时,用定义来求.
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
2.3 抛物线
2.3.1 抛物线的定义与标准方程
2.3.1
课堂互动讲练
知能优化训练
课前自主学案
学习目标
学习目标
1.掌握抛物线的定义及焦点、准线的概念.
2.会求简单的抛物线的方程.
课前自主学案
温故夯基
抛物线.
2
知新益能
相等
准线.
思考感悟
1.如何理解抛物线的定义?
提示:(1)抛物线定义的实质可归结为“一动三定”,一个动点,设为M;一个定点F即抛物线的焦点;一条定直线l即抛物线的准线;一个定值即点M与点F的距离和它到直线l的距离之比等于1.
(2)在抛物线的定义中,定点F不能在直线l上,否则,动点M的轨迹就不是抛物线,而是过点F垂直于直线l的一条直线.如到点F(1,0)与到直线l:x+y-1=0的距离相等的点的轨迹方程为x-y-1=0,轨迹为过点F且与直线l垂直的一条直线.
2.抛物线的标准方程
思考感悟
2.如何确定抛物线的焦点位置和开口方向?
提示:一次项变量为x(或y),则焦点在x轴(或y轴)上;若系数为正,则焦点在正半轴上;系数为负,则焦点在负半轴上,焦点确定,开口方向也随之确定.
四种位置的抛物线标准方程的对比:
(1)共同点:
①原点在抛物线上;②焦点在坐标轴上;
③焦点的非零坐标都是一次项系数的.
(2)不同点:
①焦点在x轴上时,方程的右端为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2;②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)负半轴上,方程右端取负号.
课堂互动讲练
确定抛物线的焦点、开口方向、准线方程
考点突破
例1
求抛物线y=2ax2(a≠0)的顶点坐标、焦点坐标、准线方程,指出其开口方向并确定p值.
自我挑战1 已知抛物线的标准方程如下,分别求其焦点坐标和准线方程.
(1)y2=6x;(2)2y2+5x=0.
求抛物线的标准方程
求抛物线的方程通常有定义法和待定系数法.由于标准方程有四种形式,因而在求方程时应首先确定焦点在哪一个半轴上,进而确定方程的形式,然后再利用已知条件确定p的值.
例2
求满足下列条件的抛物线的标准方程:
(1)过点(-3,2);
(2)焦点在直线x-2y-4=0上.
【思路点拨】 首先判断焦点可能存在的位置,设出适当的方程的形式,然后求出参数p即可.
【名师点评】 (1)确定抛物线的标准方程,从形式上看,只需求一个参数p,但由于标准方程有四种类型,因此,还应确定开口方向,当开口方向不确定时,应进行分类讨论.有时也可设标准方程的统一形式,避免讨论,如焦点在x轴上的抛物线标准方程可设为y2=2mx(m≠0),焦点在y轴上的抛物线标准方程可设为x2=2my(m≠0).
(2)求抛物线标准方程的方法:
特别注意在设标准方程时,若焦点位置不确定,要分类讨论.
抛物线的定义及其应用
对于抛物线中的最值问题,其求解方法为把到焦点的距离化为到准线的距离,到准线的距离化为到焦点的距离.
例3
【思路点拨】 先根据抛物线的定义求出抛物线方程.再利用平面几何的有关性质求出最小值.
【解】 (1)点M到点F(0,1)的距离比它到x轴的距离大1,即“点M到点F(0,1)的距离等于它到直线y=-1的距离”,所以点M的轨迹是以F为焦点,直线y=-1为准线的抛物线,此时,p=2,
故所求抛物线方程G为x2=4y.
(2011年青州高二检测)已知点A(12,6),点M到F(0,1)的距离比它到x轴的距离大1.
(1)求点M的轨迹方程G;
(2)在G上是否存在一点P,使点P到点A的距离与点P到x轴的距离之和取得最小值?若存在,求此时点P的坐标;若不存在,请说明理由.
【名师点评】 根据抛物线的定义,平面内与一个定点F和一条不过该点的直线l的距离相等的点的集合叫作抛物线,另一方面,抛物线上的任意一点到焦点的距离等于该点到准线的距离.就是说,定义具有判定和性质的双重作用,本题利用抛物线的定义求出点的轨迹方程,又利用抛物线的定义,“化曲折为平直”,将两点间的距离的和转化为点到直线的距离求得最小值,这是平面几何性质的典型运用.
自我挑战3 已知抛物线y2=4x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出取最小值时P点坐标.
解:
方法感悟
1.(1)“p”是抛物线的焦点到准线的距离,所以p的值永远大于0.特别注意,当抛物线标准方程的一次项系数为负时,不要出现错误.
(2)只有顶点在坐标原点,焦点在坐标轴上的抛物线方程才有标准形式.
(3)抛物线的开口方向取决于一次项变量(x或y)的取值范围.如抛物线x2=-2y,一次项变量y≤0,所以抛物线开口向下.
2.标准方程中只有一个参数p,求抛物线的标准方程,只需求出p的值即可,常用待定系数法.
(1)用待定系数法求抛物线标准方程时,一定先确定焦点位置与开口方向,如果开口方向不确定时,可设所求抛物线方程为y2=ax(a≠0),或者x2=ay(a≠0);
(2)当抛物线不在标准位置时,用定义来求.
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
同课章节目录
