江苏省睢宁县新世纪中学7.5《三角形的内角和(4)》教案(七年级下)
文档属性
| 名称 | 江苏省睢宁县新世纪中学7.5《三角形的内角和(4)》教案(七年级下) |
|
|
| 格式 | zip | ||
| 文件大小 | 46.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-14 00:00:00 | ||
图片预览



文档简介
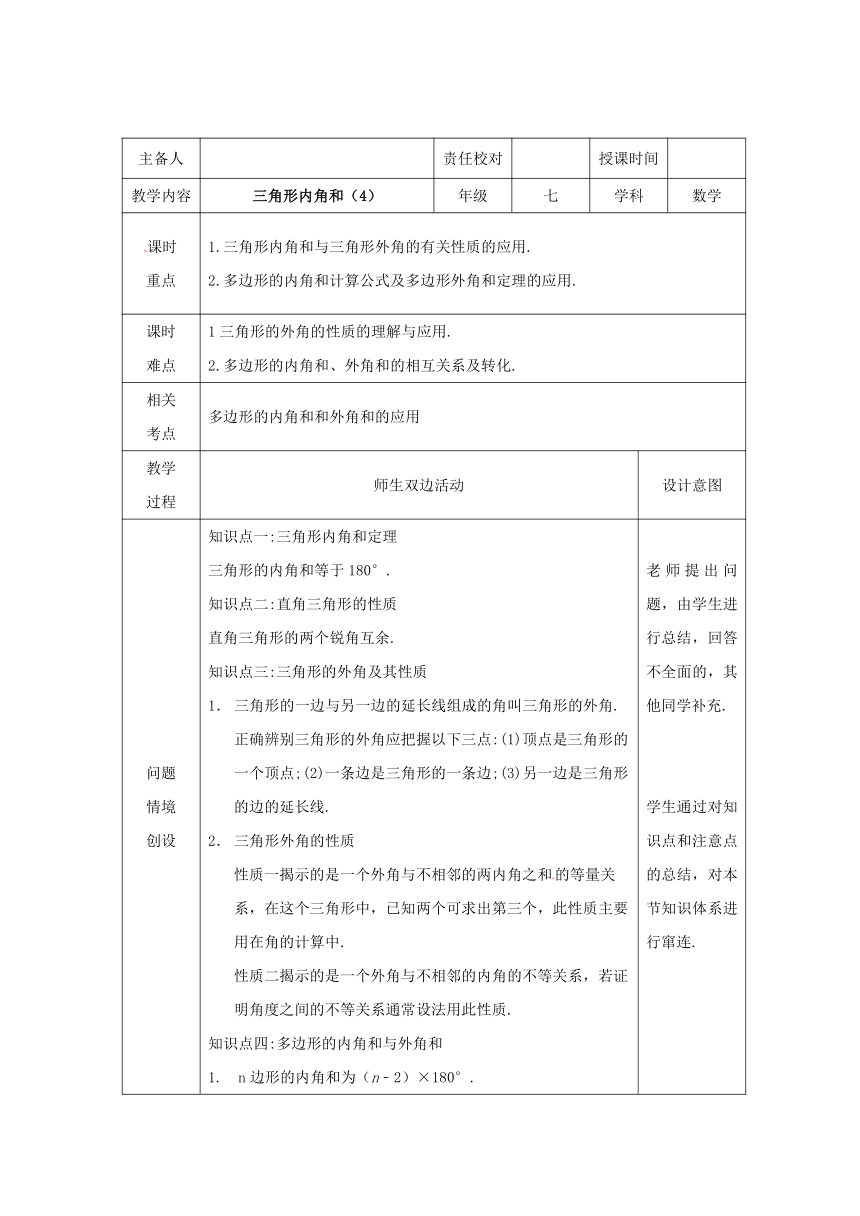
主备人 责任校对 授课时间
教学内容 三角形内角和(4) 年级 七 学科 数学
课时重点 三角形内角和与三角形外角的有关性质的应用.2.多边形的内角和计算公式及多边形外角和定理的应用.
课时难点 1三角形的外角的性质的理解与应用.2.多边形的内角和、外角和的相互关系及转化.
相关考点 多边形的内角和和外角和的应用
教学过程 师生双边活动 设计意图
问题情境创设 知识点一:三角形内角和定理三角形的内角和等于180°.知识点二:直角三角形的性质直角三角形的两个锐角互余.知识点三:三角形的外角及其性质三角形的一边与另一边的延长线组成的角叫三角形的外角.正确辨别三角形的外角应把握以下三点:(1)顶点是三角形的一个顶点;(2)一条边是三角形的一条边;(3)另一边是三角形的边的延长线.三角形外角的性质性质一揭示的是一个外角与不相邻的两内角之和的等量关系,在这个三角形中,已知两个可求出第三个,此性质主要用在角的计算中.性质二揭示的是一个外角与不相邻的内角的不等关系,若证明角度之间的不等关系通常设法用此性质.知识点四:多边形的内角和与外角和1. n边形的内角和为(n﹣2)×180°.2. n边形的对角线条数为 .3. 多边形的外角和等于360°,与边数的多少无关. 老师提出问题,由学生进行总结,回答不全面的,其他同学补充.学生通过对知识点和注意点的总结,对本节知识体系进行窜连.
教学过程 师生双边活动 设计意图
合作交流自主探究 题型一 三角形内角和定理的应用例1:已知在△ABC中,∠A﹢∠B=80°,∠C=2∠B,求∠A、∠B、∠C分析:根据三角形3个内角和等于180°,根据角之间的关系灵活变形求解.方法指导:解决本题应注意到三角形内角之间的一个重要的数量关系,即三角形内角和为180°,这是列方程的一个重要的等量关系.变式:1.如图,已知∠A=30°,求∠ABC+∠ACB+ ∠AED+∠ADE 2.E为△ABC的BC延长线上一点,DE⊥AB,垂足为D, 且∠A=62°,∠E=30°,求∠ACE. 题型二 直角三角形两锐角互余例2:如图,CD是Rt△ABC的斜边AB上的高,则在图中的四个锐角中一定有∠A=_,∠B=_ 分析:图中有三个直角三角形,根据直角三角形两锐角互余,解决本题不难.答案:∠BCD,∠ACD方法指导:分清在哪个直角三角形中,两锐角互余. 变式:1.直角三角形两锐角的平 分线相交所成的角的度数为_2.如图,AB∥CD,AC⊥BD,图中与∠CAB互余的角有_个题型三 三角形外角及性质例3:如图,∠B=10°,∠C=20°, ∠BOC=110°,求∠A解析:要求的度数,可设法让成为与已知角相等的三角形的内角或外角,于是延长BO交AC与D,则∠A,、∠B是△ABD的两个内角,故要求∠A只需要∠DOC,而∠DOC是△COD的外角∠BOC的一个不相邻的内角,由∠BOC、∠C可求出∠ODC,问题可得到解决. 巩固内角和定理,找到等量关系,列方程解题,让学生感受利用方程解题的重要思想.变式训练学生自己动手,感受和巩固三角形内角和.注意寻找直角三角形中的特殊关系,是解题的关键。当图形中出现多个直角三角形时,要分清在哪个三角形中.重点培养学生利用外角解题的能力,感受
教学过程 师生双边活动 设计意图
合作交流自主探究 答案:∠A=80°方法指导:通过添加辅助线将问题转化为三角形问题来解决是常用方法.变式:如图,AC⊥DE,垂足为O,∠B=35°,∠E=30 °,求∠ACB和∠A的度数题型四 多边形的内角和与外角和定理的应用例4:已知四边形的四个外角度数比为1:2:3:4,求各外角的度数.解析:考查四边形外角和定理,由四边形外角和定理和各外角之间的比例关系很容易求出各角.方法指导:本题应用了设未知数x的代数方法求出四边形四个外角的度数,不少几何线段的计算、角的计算以及证明题,如果应用代数方法求解可使过程简单、清晰.已知条件出现比例关系时,套用设参数是最常见的解题思路,通过设参数,结合几何知识把问题转化为解方程.变式:1.一个多边形的每个内角为120°,求多边形边数. .2.多边形的每个内角都是每个外角的4倍,求多边形的边数. .3.多边形的内角和与它的一个外角的和是2008°,则此多边形的 边形及这个外角的度数. .4.一个多边形的对角线条数等于它的边数的2倍,求它的内角和.5.已知多边形的一个内角的外角与其它各内角和为600°,求边数及相应的外角度数. 利用外角解题的简便性.通过做辅助线将问题转化为三角形问题来解题是数学中常用的方法.培养学生利用内角和和外角和定理的能力.体会运用代数方法解几何问题的数学思想.另外不要生搬硬套公式,要充分利用特殊情况灵活应用注重夯实基础,巩固概念和定理
教学过程 师生双边活动 设计意图
巩固提高运用拓展 1.(2011湖北)如图AB∥CD∥EF,∠ABC=45°,∠CEF=154°,则∠BCE等于( )A.23° B.16° C.20° D.26°2.(2011广东)正八边形的每个内角为( )A.120° B.135° C.140° D.144°3.一个多边形截去一个角后,形成的多边形的内角和是2520°,那么原多边形的边数是( )A.15 B.16 C.15或16 D.15或16或174.(2011贵州)有下列5种正多边形地砖,正三角形,正方形,正五边形,正六边形,正八边形.现要用同一种大小一样,形状相同的正多边形地砖铺设地面,其中能做到彼此不留空隙,不重叠地铺设的地砖有( )A.4种 B.3种 C.2种 D.1种 体验中考,掌握考点和考型
板书设计 课题:三角形的内角和---复习1.三角形内角和定理 例题教学 练习应用2.直角三角形性质 课堂小结3.三角形的外角及性质 作业布置4. 多边形的内角和与外角和
课后盘点自我反思 1.问题情境创设,学生系统掌握知识点.2.例题探究与讲解,培养学生利用知识的能力,训练学生利用外角定理解决问题的能力.3.外角是学生的新接受知识,学生应用时较生疏,仍习惯用内角和定理解决问题.4.本节课还应注重学生动手操作和说理分析的能力的培养.
教学内容 三角形内角和(4) 年级 七 学科 数学
课时重点 三角形内角和与三角形外角的有关性质的应用.2.多边形的内角和计算公式及多边形外角和定理的应用.
课时难点 1三角形的外角的性质的理解与应用.2.多边形的内角和、外角和的相互关系及转化.
相关考点 多边形的内角和和外角和的应用
教学过程 师生双边活动 设计意图
问题情境创设 知识点一:三角形内角和定理三角形的内角和等于180°.知识点二:直角三角形的性质直角三角形的两个锐角互余.知识点三:三角形的外角及其性质三角形的一边与另一边的延长线组成的角叫三角形的外角.正确辨别三角形的外角应把握以下三点:(1)顶点是三角形的一个顶点;(2)一条边是三角形的一条边;(3)另一边是三角形的边的延长线.三角形外角的性质性质一揭示的是一个外角与不相邻的两内角之和的等量关系,在这个三角形中,已知两个可求出第三个,此性质主要用在角的计算中.性质二揭示的是一个外角与不相邻的内角的不等关系,若证明角度之间的不等关系通常设法用此性质.知识点四:多边形的内角和与外角和1. n边形的内角和为(n﹣2)×180°.2. n边形的对角线条数为 .3. 多边形的外角和等于360°,与边数的多少无关. 老师提出问题,由学生进行总结,回答不全面的,其他同学补充.学生通过对知识点和注意点的总结,对本节知识体系进行窜连.
教学过程 师生双边活动 设计意图
合作交流自主探究 题型一 三角形内角和定理的应用例1:已知在△ABC中,∠A﹢∠B=80°,∠C=2∠B,求∠A、∠B、∠C分析:根据三角形3个内角和等于180°,根据角之间的关系灵活变形求解.方法指导:解决本题应注意到三角形内角之间的一个重要的数量关系,即三角形内角和为180°,这是列方程的一个重要的等量关系.变式:1.如图,已知∠A=30°,求∠ABC+∠ACB+ ∠AED+∠ADE 2.E为△ABC的BC延长线上一点,DE⊥AB,垂足为D, 且∠A=62°,∠E=30°,求∠ACE. 题型二 直角三角形两锐角互余例2:如图,CD是Rt△ABC的斜边AB上的高,则在图中的四个锐角中一定有∠A=_,∠B=_ 分析:图中有三个直角三角形,根据直角三角形两锐角互余,解决本题不难.答案:∠BCD,∠ACD方法指导:分清在哪个直角三角形中,两锐角互余. 变式:1.直角三角形两锐角的平 分线相交所成的角的度数为_2.如图,AB∥CD,AC⊥BD,图中与∠CAB互余的角有_个题型三 三角形外角及性质例3:如图,∠B=10°,∠C=20°, ∠BOC=110°,求∠A解析:要求的度数,可设法让成为与已知角相等的三角形的内角或外角,于是延长BO交AC与D,则∠A,、∠B是△ABD的两个内角,故要求∠A只需要∠DOC,而∠DOC是△COD的外角∠BOC的一个不相邻的内角,由∠BOC、∠C可求出∠ODC,问题可得到解决. 巩固内角和定理,找到等量关系,列方程解题,让学生感受利用方程解题的重要思想.变式训练学生自己动手,感受和巩固三角形内角和.注意寻找直角三角形中的特殊关系,是解题的关键。当图形中出现多个直角三角形时,要分清在哪个三角形中.重点培养学生利用外角解题的能力,感受
教学过程 师生双边活动 设计意图
合作交流自主探究 答案:∠A=80°方法指导:通过添加辅助线将问题转化为三角形问题来解决是常用方法.变式:如图,AC⊥DE,垂足为O,∠B=35°,∠E=30 °,求∠ACB和∠A的度数题型四 多边形的内角和与外角和定理的应用例4:已知四边形的四个外角度数比为1:2:3:4,求各外角的度数.解析:考查四边形外角和定理,由四边形外角和定理和各外角之间的比例关系很容易求出各角.方法指导:本题应用了设未知数x的代数方法求出四边形四个外角的度数,不少几何线段的计算、角的计算以及证明题,如果应用代数方法求解可使过程简单、清晰.已知条件出现比例关系时,套用设参数是最常见的解题思路,通过设参数,结合几何知识把问题转化为解方程.变式:1.一个多边形的每个内角为120°,求多边形边数. .2.多边形的每个内角都是每个外角的4倍,求多边形的边数. .3.多边形的内角和与它的一个外角的和是2008°,则此多边形的 边形及这个外角的度数. .4.一个多边形的对角线条数等于它的边数的2倍,求它的内角和.5.已知多边形的一个内角的外角与其它各内角和为600°,求边数及相应的外角度数. 利用外角解题的简便性.通过做辅助线将问题转化为三角形问题来解题是数学中常用的方法.培养学生利用内角和和外角和定理的能力.体会运用代数方法解几何问题的数学思想.另外不要生搬硬套公式,要充分利用特殊情况灵活应用注重夯实基础,巩固概念和定理
教学过程 师生双边活动 设计意图
巩固提高运用拓展 1.(2011湖北)如图AB∥CD∥EF,∠ABC=45°,∠CEF=154°,则∠BCE等于( )A.23° B.16° C.20° D.26°2.(2011广东)正八边形的每个内角为( )A.120° B.135° C.140° D.144°3.一个多边形截去一个角后,形成的多边形的内角和是2520°,那么原多边形的边数是( )A.15 B.16 C.15或16 D.15或16或174.(2011贵州)有下列5种正多边形地砖,正三角形,正方形,正五边形,正六边形,正八边形.现要用同一种大小一样,形状相同的正多边形地砖铺设地面,其中能做到彼此不留空隙,不重叠地铺设的地砖有( )A.4种 B.3种 C.2种 D.1种 体验中考,掌握考点和考型
板书设计 课题:三角形的内角和---复习1.三角形内角和定理 例题教学 练习应用2.直角三角形性质 课堂小结3.三角形的外角及性质 作业布置4. 多边形的内角和与外角和
课后盘点自我反思 1.问题情境创设,学生系统掌握知识点.2.例题探究与讲解,培养学生利用知识的能力,训练学生利用外角定理解决问题的能力.3.外角是学生的新接受知识,学生应用时较生疏,仍习惯用内角和定理解决问题.4.本节课还应注重学生动手操作和说理分析的能力的培养.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
