江苏省睢宁县新世纪中学7.4《三角形的认识(3)》教案(七年级下)
文档属性
| 名称 | 江苏省睢宁县新世纪中学7.4《三角形的认识(3)》教案(七年级下) |
|
|
| 格式 | zip | ||
| 文件大小 | 64.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-14 00:00:00 | ||
图片预览



文档简介
主备人 责任校对 授课时间
教学内容 7.4 三角形的认识(3) 年级 七 学科 数学
课时重点 三角形三边关系的应用,构成三角形的条件.会画任意三角形的高,中线,角平分线,并会用三角形的三条线段解决问题.
课时难点 1. 三角形三边关系的应用.2. 钝角三角形的高线的画法.
相关考点 三角形三边关系及构成三角形的条件
教学过程 师生双边活动 设计意图
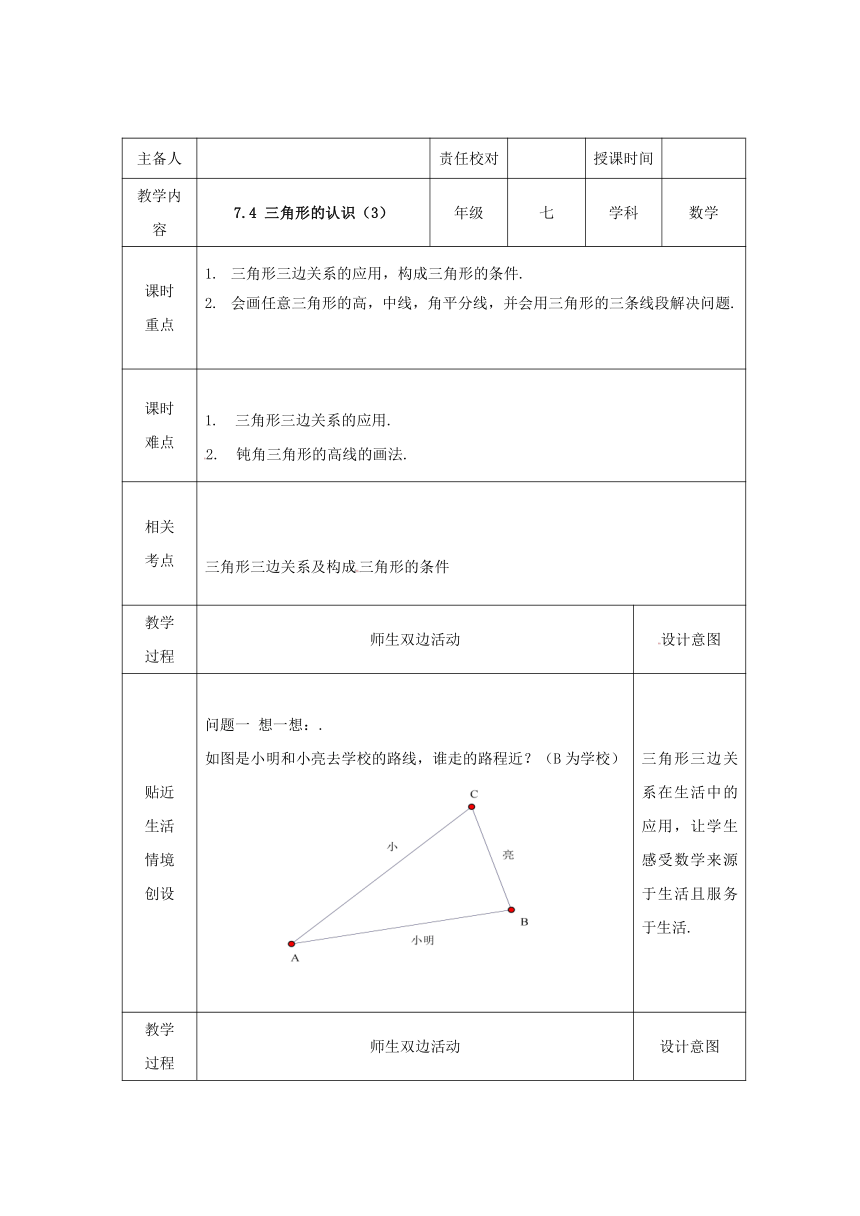
贴近生活情境创设 问题一 想一想:.如图是小明和小亮去学校的路线,谁走的路程近?(B为学校) 三角形三边关系在生活中的应用,让学生感受数学来源于生活且服务于生活.
教学过程 师生双边活动 设计意图
贴近生活情境创设 【相关练习】已知a,b,c为△ABC的三边,化简:. 问题二 请你帮助小明:.小明生日时收到一块三角形的生日蛋糕,小亮给他出了个问题让他把蛋糕平均分成四块,应该怎么切?(图形不唯一,请学生到黑板画出图形,教师最后总结) 等. 三角形三边关系与其他知识的联系,让学生能够感受到知识之间的内在联系.“三角形的一条中线将元三角形分成面积相等的两部分”这一命题在解“等积变换”问题中经常用到,在生产和生活中也经常用到.
合作交流自主探究 教 学过 程 1.作图(1)画出△ABC的中线AD;(2)画出△ABC的高BE,△ACD的高CF. 师生双边关系 找准三角形,画出高.设计意图
合作交流自主探究 2.如图是3X4的正方形网格(每个小正方形的边长为1),点A,B,C,D,E,F,G都在格点上,请解答下列各题:(1) 在图一中画一个面积为1的直角三角形(三角形的顶点从以上七个点中选择);(2)在图二中画一个面积的钝角三角形(三角形的顶点从以上七个点中选择);(3)请写出面积为2的钝角三角形. 三角形面积的相关知识与网格联系起来,让学生利用网格的固有条件解决问题.
巩固练习能力提高 1.(2011 金华)已知三角形的两边长为4,8,则第三遍的长度可以是________ (写一个即可)2.(2007 柳州)如果三角形的两条边长分别为23cm和10cm,第三边与其中一边的长相等,那么第三边的长为_________cm.3.(2004 嘉兴)小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三个摆成一个三角形,那么他选的三根木棒的长度分别是:_____, _____, ______(单位:cm)4.如图,S△ABC=1,S△BDE=S△DEC=S△ACE.求△ADE得面积. 联系中考,把握方向.
教学过程 师生双边关系 设计意图
巩固练习能力提高 5.观察并探求下列各问题,写出你所观察得到的结论. (1)如图,△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由.(2)将(1)中点P移至△ABC内,得图②,试观察比较 △BPC的周长与△ABC的周长的大小,并说明理由. (3)将(2)中点P变为两个点P1、P2得下图,试观察比较 四边形BP1P2C的周长 由易到难,让(4)将(3)中的点P1、P2移至△ABC外,并使点P1、P2 学生认识到在与点A在边BC的异侧,且∠P1BC<∠ABC,∠P2CB<∠ACB, 三角形中比较如图,试观察比较四边形BP1P2C的周长与△ABC的周长的大小线段长短,应并说明理由. (5)若将(3)中的四边形BP1P2C的顶点B、C移至△ABC内,得四边形B1P1P2C1,如图⑤,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.
板书设计 7.4 认识三角形(3)问题一 三边关系解决路程问题 问题二 把三角形分成面积相等部分
课后盘点自我反思 1.情境创设,从与生活相关的问题出发,让学生轻松进入学习状态,并能提高他们的积极性.2问题二中让学生发挥想象,大胆猜想,然后相互交流来达到深刻记忆效果.3.本节是认识三角形的复习课,主要是让学生巩固之前所学的知识,并在此基础上解决问题,达到学以致用的目的.
教学内容 7.4 三角形的认识(3) 年级 七 学科 数学
课时重点 三角形三边关系的应用,构成三角形的条件.会画任意三角形的高,中线,角平分线,并会用三角形的三条线段解决问题.
课时难点 1. 三角形三边关系的应用.2. 钝角三角形的高线的画法.
相关考点 三角形三边关系及构成三角形的条件
教学过程 师生双边活动 设计意图
贴近生活情境创设 问题一 想一想:.如图是小明和小亮去学校的路线,谁走的路程近?(B为学校) 三角形三边关系在生活中的应用,让学生感受数学来源于生活且服务于生活.
教学过程 师生双边活动 设计意图
贴近生活情境创设 【相关练习】已知a,b,c为△ABC的三边,化简:. 问题二 请你帮助小明:.小明生日时收到一块三角形的生日蛋糕,小亮给他出了个问题让他把蛋糕平均分成四块,应该怎么切?(图形不唯一,请学生到黑板画出图形,教师最后总结) 等. 三角形三边关系与其他知识的联系,让学生能够感受到知识之间的内在联系.“三角形的一条中线将元三角形分成面积相等的两部分”这一命题在解“等积变换”问题中经常用到,在生产和生活中也经常用到.
合作交流自主探究 教 学过 程 1.作图(1)画出△ABC的中线AD;(2)画出△ABC的高BE,△ACD的高CF. 师生双边关系 找准三角形,画出高.设计意图
合作交流自主探究 2.如图是3X4的正方形网格(每个小正方形的边长为1),点A,B,C,D,E,F,G都在格点上,请解答下列各题:(1) 在图一中画一个面积为1的直角三角形(三角形的顶点从以上七个点中选择);(2)在图二中画一个面积的钝角三角形(三角形的顶点从以上七个点中选择);(3)请写出面积为2的钝角三角形. 三角形面积的相关知识与网格联系起来,让学生利用网格的固有条件解决问题.
巩固练习能力提高 1.(2011 金华)已知三角形的两边长为4,8,则第三遍的长度可以是________ (写一个即可)2.(2007 柳州)如果三角形的两条边长分别为23cm和10cm,第三边与其中一边的长相等,那么第三边的长为_________cm.3.(2004 嘉兴)小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三个摆成一个三角形,那么他选的三根木棒的长度分别是:_____, _____, ______(单位:cm)4.如图,S△ABC=1,S△BDE=S△DEC=S△ACE.求△ADE得面积. 联系中考,把握方向.
教学过程 师生双边关系 设计意图
巩固练习能力提高 5.观察并探求下列各问题,写出你所观察得到的结论. (1)如图,△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由.(2)将(1)中点P移至△ABC内,得图②,试观察比较 △BPC的周长与△ABC的周长的大小,并说明理由. (3)将(2)中点P变为两个点P1、P2得下图,试观察比较 四边形BP1P2C的周长 由易到难,让(4)将(3)中的点P1、P2移至△ABC外,并使点P1、P2 学生认识到在与点A在边BC的异侧,且∠P1BC<∠ABC,∠P2CB<∠ACB, 三角形中比较如图,试观察比较四边形BP1P2C的周长与△ABC的周长的大小线段长短,应并说明理由. (5)若将(3)中的四边形BP1P2C的顶点B、C移至△ABC内,得四边形B1P1P2C1,如图⑤,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.
板书设计 7.4 认识三角形(3)问题一 三边关系解决路程问题 问题二 把三角形分成面积相等部分
课后盘点自我反思 1.情境创设,从与生活相关的问题出发,让学生轻松进入学习状态,并能提高他们的积极性.2问题二中让学生发挥想象,大胆猜想,然后相互交流来达到深刻记忆效果.3.本节是认识三角形的复习课,主要是让学生巩固之前所学的知识,并在此基础上解决问题,达到学以致用的目的.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
