江苏省睢宁县新世纪中学7.1《探索直线平行的条件(1)》教案(七年级下)
文档属性
| 名称 | 江苏省睢宁县新世纪中学7.1《探索直线平行的条件(1)》教案(七年级下) |
|
|
| 格式 | zip | ||
| 文件大小 | 128.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-14 00:00:00 | ||
图片预览



文档简介
主备人 责任校对 授课时间
教学内容 探索直线平行的条件(第一课时) 年级 七 学科 数学
课时重点 (1)识别同位角 (2)用同位角相等判定两条直线平行
课时难点 用同位角相等判定两条直线平行
相关考点 用同位角相等判定两条直线平行
教学过程 师生双边活动 设计意图
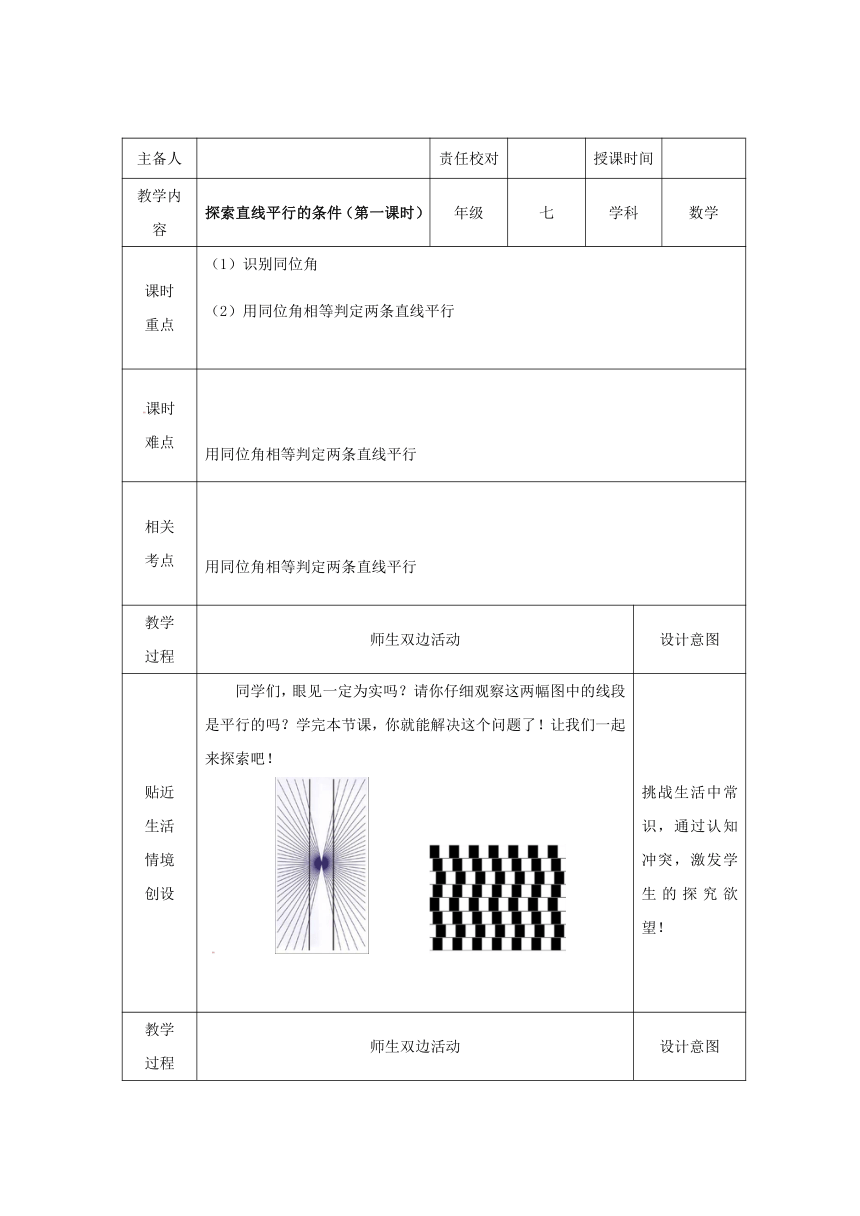
贴近生活情境创设 同学们,眼见一定为实吗?请你仔细观察这两幅图中的线段是平行的吗?学完本节课,你就能解决这个问题了!让我们一起来探索吧! 挑战生活中常识,通过认知冲突,激发学生的探究欲望!
教学过程 师生双边活动 设计意图
合作交流自主探究教学过程师 1、认识同位角画一画两条直线AB、 CD与直线EF相交,交点分别为E F如图 则称直线AB 、CD 被直线EF所截,直线EF为截线。 图说一说二条直线AB 、CD 被直线EF所截可得8个角,即所谓“三线八角”。 这八个角中对顶角、邻补角各有哪些?感悟同位角:两条直线被第三条直线所截,在二条直线的同侧,且在第三条直线的同旁的二个角叫同位角。如图中的∠1与∠5分别在直线AB、 CD的上侧,又在第三条直线EF的右侧,所以∠1与∠5是同位角,它们的位置相同,在图中还有∠2与∠6,∠4与∠8,∠3与∠7也是同位角。做一做 如图,同位角各有多少对?师生双边活动 从学生已有的知识入手,自然复习同一平面内两条直线的位置关系以及平行、相交的基本图形和基本知识,承上启下为新课的学习做好铺垫。设计意图
合作交流自主探究教学过程巩固提高运用拓展 2、认识同位角的注意点(1)看它们是不是在一条直线的同侧,(2)看截它们的两条直线是什么,这两个角是不是在截它们的直线的同旁。也就是说,是否满足“F”型。讨论两条直线被第三条直线所截,转动直线b,当直线b转动到不同的位置时,从的大小变化说出这两条直线的位置关系。在这个过程中,存在着一个平行的位置关系,那么与有何关系时,这两条线平行呢?双向沟通我们在用三角板平推法画平行线时还发现:画平行线仍借助了第三条直线,但是要用与a、b都相交的第三线,根据“三线八角”的名称,在画平行线的过程中,实际上是保证了同位的两个角都是450,从而得出:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。可以简单说成:同位角相等,两直线平行议一议1、如图1∠1=150°,∠2=150°, a//b吗?2、如图2∠C=31°,当∠ABE= 度时,就能使BE//CD?师生双边活动类型之一 直接运用例1、如图所示:∠1=∠C,∠2=∠C请你找出图中互相平行的直线,并说明理由思路分析 在图中找到∠1,∠C,∠2的位置,易知∠1,∠2是同位角,∠C,∠2是同位角,于是由“同位角相等,两直线平行。”可知,AB∥C点评 用“同位角相等,两直线平行”是判定两条直线平行的有效方法例2如图 直线a、b被直线c所截,∠1=35°,∠2=145°,问:直线a与b平行吗?思路分析 考虑到要运用“同位角相等,两直线平行。”来判断两直线是否平行,而所给一角是∠1=35°.∠2=145°,于是可以由∠2=145°求得∠3=35°,则可知结果。点评 在图形中准确地找到必需同位角是解题的前提。提问:现在你能判断两幅图中的线段是否平行了吗?巩固练习:1.如图,∠1和∠2是同位角的是( ) A B C D 从实物抽象到几何图形是对学生能力的一种培养,通过学生的讨论,归纳总结,得出结论,使学生对平行线的判定方法有深刻的认识,同时培养学生的归纳总结能力。设计意图通过对问题的解决着力于引导学生有根有据地说理培养学生的说理能力
教学过程巩固提高运用拓展 师生双边活动2. 如图1,∠1和∠2是直线_______和直线________被直线_____所截得的同位角,将直线的交点用大写字母标出来,并指出图中其他的同位角。如图2 已知四条直线AB,BC,AC,DE。问:①∠1与∠2是直线______和直线______被直线_____所截而成的____角.②∠6与∠7是直线_____和直线_____被直线。来,并指出图中其他的同位角。 3.如图,竖在地面上的两根旗杆,它们平行吗?请说明道理。4.如图① ∵ ∠2 =∠4(已知) ∴ ∥ ( )② ∵ = (已知) ∴ CD∥BF(同位角相等,两直线平行)总结本节课学习的数学知识: “三线八角”、同位角的概念以及“同位角相等,两直线平行”本节课学习的数学方法:(1)转化思想。(2)运用“同位角相等,两直线平行”判定两条直线平行。反思1、什么是“三线八角”?什么样的角才能称得上是同位角?如何判定两条直线平行? 设计意图通过练习巩固已经学过的知识,使学生加深对已学知识的理解与掌握
板书设计 情景导入探索直线平行的条件同位角相等,两直线平行应用新知四.巩固练习
课后盘点自我反思 探索直线平行的条件让我的体会最深之一就是怎样让学生自主探索两直线平行的条件,这与以前的教学方法完全不同的就是:引导学生参与整个探索过程,通过活动教具的演示,使学生真正理解和掌握“同位角相等,两直线平等”并能够用自己的语言概括出这一重要结论;课堂上在与学生的对话、学生回答问题时,能有意识地锻炼学生使用规范性的几何语言;3.注重由学生从临摹书写到自主书写,锻炼学生的动手能力
图1
c
c
c
图8888888.288.110101010
c
c
教学内容 探索直线平行的条件(第一课时) 年级 七 学科 数学
课时重点 (1)识别同位角 (2)用同位角相等判定两条直线平行
课时难点 用同位角相等判定两条直线平行
相关考点 用同位角相等判定两条直线平行
教学过程 师生双边活动 设计意图
贴近生活情境创设 同学们,眼见一定为实吗?请你仔细观察这两幅图中的线段是平行的吗?学完本节课,你就能解决这个问题了!让我们一起来探索吧! 挑战生活中常识,通过认知冲突,激发学生的探究欲望!
教学过程 师生双边活动 设计意图
合作交流自主探究教学过程师 1、认识同位角画一画两条直线AB、 CD与直线EF相交,交点分别为E F如图 则称直线AB 、CD 被直线EF所截,直线EF为截线。 图说一说二条直线AB 、CD 被直线EF所截可得8个角,即所谓“三线八角”。 这八个角中对顶角、邻补角各有哪些?感悟同位角:两条直线被第三条直线所截,在二条直线的同侧,且在第三条直线的同旁的二个角叫同位角。如图中的∠1与∠5分别在直线AB、 CD的上侧,又在第三条直线EF的右侧,所以∠1与∠5是同位角,它们的位置相同,在图中还有∠2与∠6,∠4与∠8,∠3与∠7也是同位角。做一做 如图,同位角各有多少对?师生双边活动 从学生已有的知识入手,自然复习同一平面内两条直线的位置关系以及平行、相交的基本图形和基本知识,承上启下为新课的学习做好铺垫。设计意图
合作交流自主探究教学过程巩固提高运用拓展 2、认识同位角的注意点(1)看它们是不是在一条直线的同侧,(2)看截它们的两条直线是什么,这两个角是不是在截它们的直线的同旁。也就是说,是否满足“F”型。讨论两条直线被第三条直线所截,转动直线b,当直线b转动到不同的位置时,从的大小变化说出这两条直线的位置关系。在这个过程中,存在着一个平行的位置关系,那么与有何关系时,这两条线平行呢?双向沟通我们在用三角板平推法画平行线时还发现:画平行线仍借助了第三条直线,但是要用与a、b都相交的第三线,根据“三线八角”的名称,在画平行线的过程中,实际上是保证了同位的两个角都是450,从而得出:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。可以简单说成:同位角相等,两直线平行议一议1、如图1∠1=150°,∠2=150°, a//b吗?2、如图2∠C=31°,当∠ABE= 度时,就能使BE//CD?师生双边活动类型之一 直接运用例1、如图所示:∠1=∠C,∠2=∠C请你找出图中互相平行的直线,并说明理由思路分析 在图中找到∠1,∠C,∠2的位置,易知∠1,∠2是同位角,∠C,∠2是同位角,于是由“同位角相等,两直线平行。”可知,AB∥C点评 用“同位角相等,两直线平行”是判定两条直线平行的有效方法例2如图 直线a、b被直线c所截,∠1=35°,∠2=145°,问:直线a与b平行吗?思路分析 考虑到要运用“同位角相等,两直线平行。”来判断两直线是否平行,而所给一角是∠1=35°.∠2=145°,于是可以由∠2=145°求得∠3=35°,则可知结果。点评 在图形中准确地找到必需同位角是解题的前提。提问:现在你能判断两幅图中的线段是否平行了吗?巩固练习:1.如图,∠1和∠2是同位角的是( ) A B C D 从实物抽象到几何图形是对学生能力的一种培养,通过学生的讨论,归纳总结,得出结论,使学生对平行线的判定方法有深刻的认识,同时培养学生的归纳总结能力。设计意图通过对问题的解决着力于引导学生有根有据地说理培养学生的说理能力
教学过程巩固提高运用拓展 师生双边活动2. 如图1,∠1和∠2是直线_______和直线________被直线_____所截得的同位角,将直线的交点用大写字母标出来,并指出图中其他的同位角。如图2 已知四条直线AB,BC,AC,DE。问:①∠1与∠2是直线______和直线______被直线_____所截而成的____角.②∠6与∠7是直线_____和直线_____被直线。来,并指出图中其他的同位角。 3.如图,竖在地面上的两根旗杆,它们平行吗?请说明道理。4.如图① ∵ ∠2 =∠4(已知) ∴ ∥ ( )② ∵ = (已知) ∴ CD∥BF(同位角相等,两直线平行)总结本节课学习的数学知识: “三线八角”、同位角的概念以及“同位角相等,两直线平行”本节课学习的数学方法:(1)转化思想。(2)运用“同位角相等,两直线平行”判定两条直线平行。反思1、什么是“三线八角”?什么样的角才能称得上是同位角?如何判定两条直线平行? 设计意图通过练习巩固已经学过的知识,使学生加深对已学知识的理解与掌握
板书设计 情景导入探索直线平行的条件同位角相等,两直线平行应用新知四.巩固练习
课后盘点自我反思 探索直线平行的条件让我的体会最深之一就是怎样让学生自主探索两直线平行的条件,这与以前的教学方法完全不同的就是:引导学生参与整个探索过程,通过活动教具的演示,使学生真正理解和掌握“同位角相等,两直线平等”并能够用自己的语言概括出这一重要结论;课堂上在与学生的对话、学生回答问题时,能有意识地锻炼学生使用规范性的几何语言;3.注重由学生从临摹书写到自主书写,锻炼学生的动手能力
图1
c
c
c
图8888888.288.110101010
c
c
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
