高中数学湘教版选修2-1:(课件)空间向量 本章优化总结
文档属性
| 名称 | 高中数学湘教版选修2-1:(课件)空间向量 本章优化总结 |

|
|
| 格式 | zip | ||
| 文件大小 | 739.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 08:02:51 | ||
图片预览




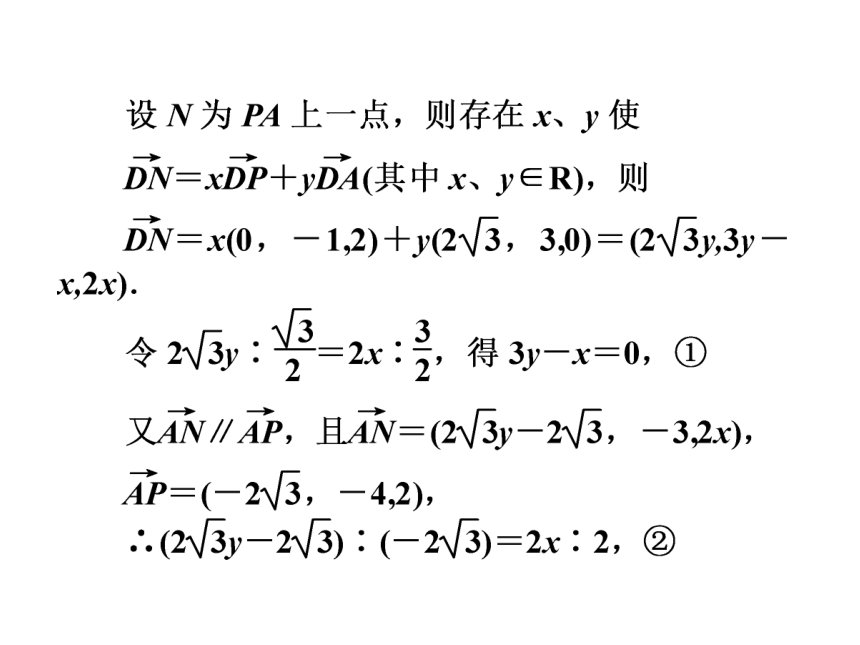
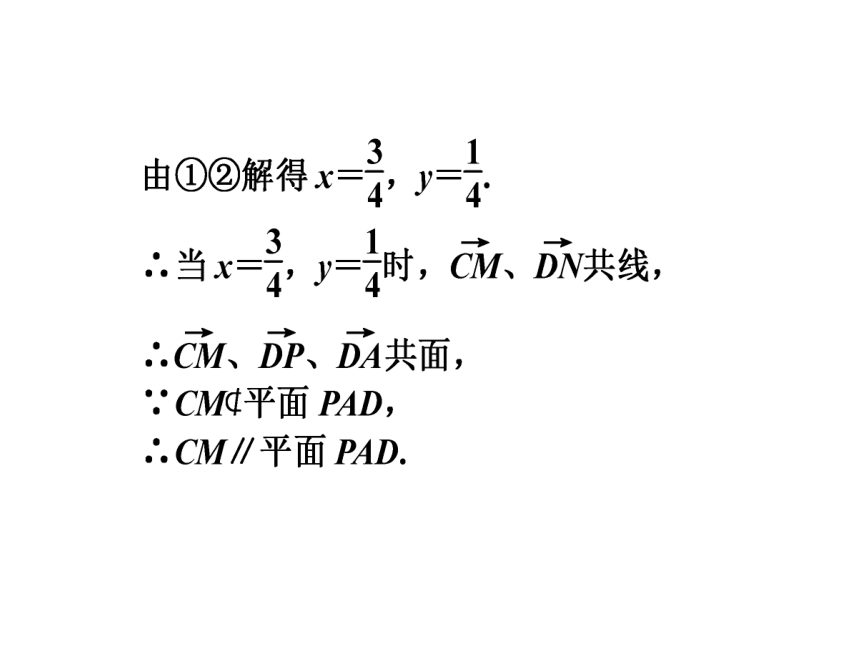



文档简介
(共39张PPT)
本章优化总结
专题探究精讲
本章优化总结
知识体系网络
章末综合检测
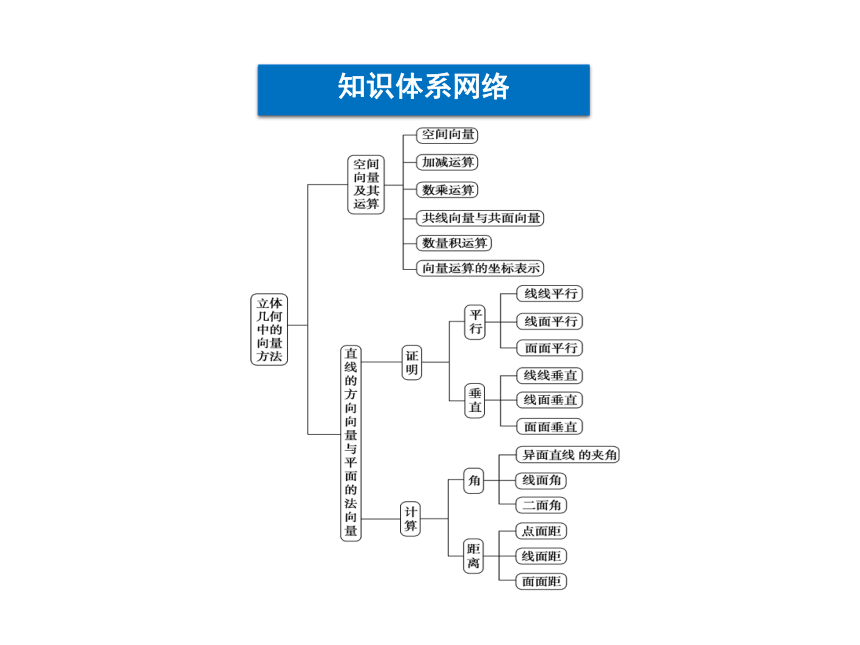
知识体系网络
专题探究精讲
空间向量与空间位置关系
用向量方法证明平行与垂直问题的一般步骤是:
(1)建立立体图形与空间向量的关系,利用空间向量表示问题中所涉及到的点、线、面,把立体几何问题转化为空间向量问题.
(2)通过向量的运算研究平行或垂直关系,有时可借助于方向向量或法向量.
(3)根据运算结果解释相关的问题.
例1
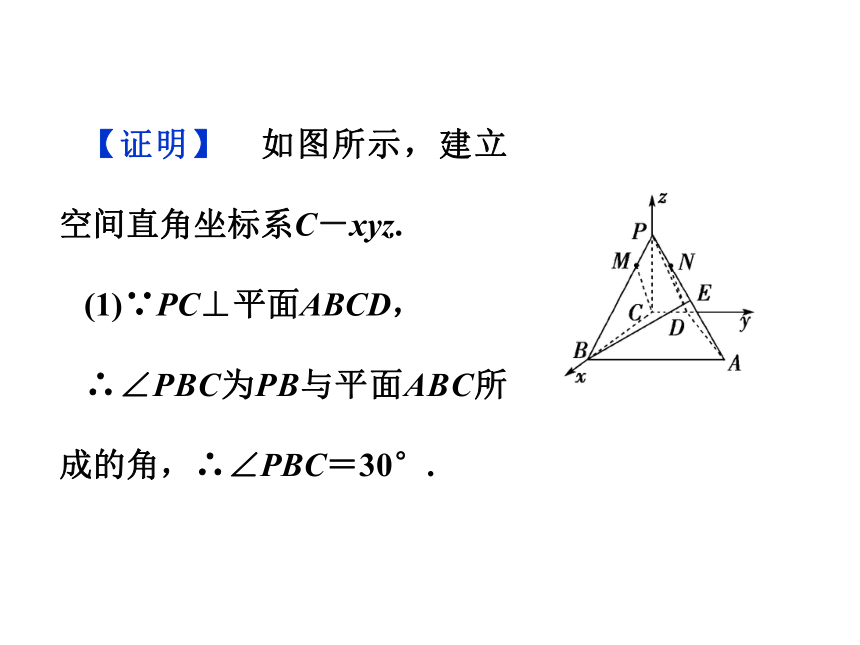
已知,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,且PB=4PM,PB与平面ABC成30°角.求证:
(1)CM∥平面PAD;
(2)平面PAB⊥平面PAD.
【思路点拨】 条件中有诸多垂直关系,具备建立空间直角坐标系的条件,可以利用向量解决.
【证明】 如图所示,建立空间直角坐标系C-xyz.
(1)∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABC所成的角,∴∠PBC=30°.
【名师点评】 在用向量方法证明平行和垂直时,同样需要立体几何最基本的定理,比如本题中,要证明直线与平面平行,我们现在还没有更好的计算手段,必须依靠直线与平面平行的判定定理来证明直线的方向向量与平面内的某个向量共线,从而得到直线和平面平行.
空间向量与空间角
(1)求异面直线所成的角
设两异面直线的方向向量分别为n1、n2,那么这两条异面直线所成的角为θ=〈n1,n2〉或θ=π-〈n1,n2〉,
∴cosθ=|cos〈n1,n2〉|.
(2)求斜线与平面所成的角
如图,设平面α的法向量为n1,斜线OA的方向向量为n2,斜线OA与平面所成的角为θ,则sinθ=|cos〈n1,n2〉|.
(3)求二面角的大小
如图,设平面α、β的法向量分别为n1、n2.因为两平面的法向量所成的角(或其补角)就等于平面α、β所成的锐二面角θ,所以cosθ=|cos〈n1,n2〉|.(注:其中的〈n1,n2〉表示向量n1与n2所成的角).
例2
【思路点拨】 可建立空间直角坐标系,求出两个平面的法向量,通过法向量的夹角进行求解.
【名师点评】 此题所求的二面角是一个无棱二面角,对于这种求无棱二面角的问题,用空间向量求解时,无需作出二面角的平面角,从而体现了空间向量的重要作用.
利用空间向量求距离
例3
已知空间中点的坐标为A(2,3,1),B(4,1,2),C(6,3,6),D(-5,-4,8),求点D到平面ABC的距离.
【名师点评】 用向量的知识来解决立体几何问题是现在高考出题的一个趋势,要将立体几何的问题转化为与向量有关的知识,因为引入向量之后简化了一些繁琐的作辅助线寻找垂线,平面角等步骤,为了更好地利用向量的特点,一般都要在解决的图形中建立坐标系,经常是利用图形中的垂直直线来建坐标系.
解题即是对命题的转化,解题中要注意将立体几何问题向平面几何问题转化,即立体问题平面化.在论证线线、线面、面面关系中的平行与垂直问题时,要注意平行与垂直关系的转化,求角与距离时应将空间中的距离与角转化为向量的投影的长度或向量的夹角.
转化与化归的数学思想
例4
【解】 (1)证明:取AC中点O,连接OS、OB.
∵SA=SC,AB=BC,∴AC⊥SO且AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,
∴SO⊥平面ABC,∴SO⊥BO.
【名师点评】 本题中(2)的求解是将二面角问题转化为两平面法向量的夹角,而(3)中点到平面的距离的求解是将所求距离转化为向量的投影的长度,这两种转化方法是立体几何问题的常见解法,使用这两种方法时要将点的坐标写准,平面的法向量求正确.
存在性问题即在一定条件下论证会不会出现某个结论.这类题型常以适合某种条件的结论“存在”、“不存在”、“是否存在”等语句表述.解答这类问题,一般要先对结论作出肯定的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,若导致合理的结论,则存在性也随之解决;若导致矛盾,则否定了存在性.
利用空间向量解决存在性问题
(2011年高考浙江卷)如图,在三棱锥P?ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2.
(1)证明:AP⊥BC;
(2)在线段AP上是否存在点M,使得二面角A?MC?B为直二面角?若存在,求出AM的长;若不存在,请说明理由.
例5
【名师点评】 本题考查空间点、线、面位置关系、二面角的求法以及空间向量的应用,也涉及空间想象能力和运算求解能力.难度适中.
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
本章优化总结
专题探究精讲
本章优化总结
知识体系网络
章末综合检测
知识体系网络
专题探究精讲
空间向量与空间位置关系
用向量方法证明平行与垂直问题的一般步骤是:
(1)建立立体图形与空间向量的关系,利用空间向量表示问题中所涉及到的点、线、面,把立体几何问题转化为空间向量问题.
(2)通过向量的运算研究平行或垂直关系,有时可借助于方向向量或法向量.
(3)根据运算结果解释相关的问题.
例1
已知,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,且PB=4PM,PB与平面ABC成30°角.求证:
(1)CM∥平面PAD;
(2)平面PAB⊥平面PAD.
【思路点拨】 条件中有诸多垂直关系,具备建立空间直角坐标系的条件,可以利用向量解决.
【证明】 如图所示,建立空间直角坐标系C-xyz.
(1)∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABC所成的角,∴∠PBC=30°.
【名师点评】 在用向量方法证明平行和垂直时,同样需要立体几何最基本的定理,比如本题中,要证明直线与平面平行,我们现在还没有更好的计算手段,必须依靠直线与平面平行的判定定理来证明直线的方向向量与平面内的某个向量共线,从而得到直线和平面平行.
空间向量与空间角
(1)求异面直线所成的角
设两异面直线的方向向量分别为n1、n2,那么这两条异面直线所成的角为θ=〈n1,n2〉或θ=π-〈n1,n2〉,
∴cosθ=|cos〈n1,n2〉|.
(2)求斜线与平面所成的角
如图,设平面α的法向量为n1,斜线OA的方向向量为n2,斜线OA与平面所成的角为θ,则sinθ=|cos〈n1,n2〉|.
(3)求二面角的大小
如图,设平面α、β的法向量分别为n1、n2.因为两平面的法向量所成的角(或其补角)就等于平面α、β所成的锐二面角θ,所以cosθ=|cos〈n1,n2〉|.(注:其中的〈n1,n2〉表示向量n1与n2所成的角).
例2
【思路点拨】 可建立空间直角坐标系,求出两个平面的法向量,通过法向量的夹角进行求解.
【名师点评】 此题所求的二面角是一个无棱二面角,对于这种求无棱二面角的问题,用空间向量求解时,无需作出二面角的平面角,从而体现了空间向量的重要作用.
利用空间向量求距离
例3
已知空间中点的坐标为A(2,3,1),B(4,1,2),C(6,3,6),D(-5,-4,8),求点D到平面ABC的距离.
【名师点评】 用向量的知识来解决立体几何问题是现在高考出题的一个趋势,要将立体几何的问题转化为与向量有关的知识,因为引入向量之后简化了一些繁琐的作辅助线寻找垂线,平面角等步骤,为了更好地利用向量的特点,一般都要在解决的图形中建立坐标系,经常是利用图形中的垂直直线来建坐标系.
解题即是对命题的转化,解题中要注意将立体几何问题向平面几何问题转化,即立体问题平面化.在论证线线、线面、面面关系中的平行与垂直问题时,要注意平行与垂直关系的转化,求角与距离时应将空间中的距离与角转化为向量的投影的长度或向量的夹角.
转化与化归的数学思想
例4
【解】 (1)证明:取AC中点O,连接OS、OB.
∵SA=SC,AB=BC,∴AC⊥SO且AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,
∴SO⊥平面ABC,∴SO⊥BO.
【名师点评】 本题中(2)的求解是将二面角问题转化为两平面法向量的夹角,而(3)中点到平面的距离的求解是将所求距离转化为向量的投影的长度,这两种转化方法是立体几何问题的常见解法,使用这两种方法时要将点的坐标写准,平面的法向量求正确.
存在性问题即在一定条件下论证会不会出现某个结论.这类题型常以适合某种条件的结论“存在”、“不存在”、“是否存在”等语句表述.解答这类问题,一般要先对结论作出肯定的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,若导致合理的结论,则存在性也随之解决;若导致矛盾,则否定了存在性.
利用空间向量解决存在性问题
(2011年高考浙江卷)如图,在三棱锥P?ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2.
(1)证明:AP⊥BC;
(2)在线段AP上是否存在点M,使得二面角A?MC?B为直二面角?若存在,求出AM的长;若不存在,请说明理由.
例5
【名师点评】 本题考查空间点、线、面位置关系、二面角的求法以及空间向量的应用,也涉及空间想象能力和运算求解能力.难度适中.
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
同课章节目录
