2020-2021学年湘教版 八年级下册期末测试卷(word版含答案)
文档属性
| 名称 | 2020-2021学年湘教版 八年级下册期末测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-25 20:37:00 | ||
图片预览



文档简介
1263650010642600湘教版2021八年级下期末测试卷
班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 15 小题 ,每题 3 分 ,共计45分 , )
?1. 以下列各组数为三角形的边长,能构成直角三角形的是(???)
A.8,12,17; B.6,8,10; C.1,2,3; D.5,12,9
?2. 已知直角三角形的两边分别为6和8,则斜边上的中线长为( )
A.20 B.5 C.4 D.4或5
?3. 如图,在△ABC中,延长BC至D,使得CD=12BC,过AC中点E作EF//CD?(点F位于点E右侧),且EF=2CD,连接DF,若AB=8,则DF的长为(? ? ? ? )?
A.3 B.4 C.23 D.32
?4. 如图所示,在?ABCD中,∠BAD=120?,连接BD,作AE?//?BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是(? ? ? ? )
A.2 B.3 C.2 D.1
?5. 在?ABCD中,AB⊥AC,∠B=60?,AC=2falsecm,则?ABCD的周长是( )
A.10cm B.11cm C.12cm D.13cm
?6. 如图,在菱形ABCD中,AC与BD相交于点O,CE⊥AB,若OC=2,BE=7,则菱形ABCD的面积为(????????)
A.813 B.613 C.815 D.615
?7. 已知点A(1,?2),AC⊥x轴,垂足为C,则点C的坐标为( )
A.(1,?0) B.(0,?1) C.(2,?0) D.(0,?2)
?
8. 下列选项中的图形,不属于中心对称图形的是 (????????)
A.等边三角形 B.正方形 C.正六边形 D.圆
?9. 函数y=x?13?x的自变量x的取值范围是( )
A.1≤x≤3 B.1?10. 对于函数y=?5x+1,下列结论:
①它的图象必经过点(?1,?5);②它的图象经过第一、二、三象限;③当x>1时,y<0;④y的值随x值的增大而增大.
其中正确的个数是( )
A.0 B.1 C.2 D.3
?11. 已知y是x的函数,y与x?1成正比例,如果这个函数的图象经过点(a,?a)(a≠0),那么它的图象大致是( )
A. B. C. D.
?12. 对某中学70名女生进行测量,得到一组数据的最大值169cm,最小值143cm,对这组数据整理时测定它的组距5cm,应分组数( )
A.5组 B.6组 C.7组 D.8组
?13. 若直线y=kx+k+1经过点(m,?n+3)和(m+1,?2n?1),且0 A.4 B.5 C.6 D.7
?14. 如图,平面直角坐标系中放置一个直角三角板OAB,∠OAB=60?,顶点A的坐标为(?1,?0),现将该三角板向右平移使点A与点O重合,得到△OCB',则点B的对应点B'的坐标是( )
A.(1,?0) B.(3,3) C.(1,?3) D.(?1,?3)
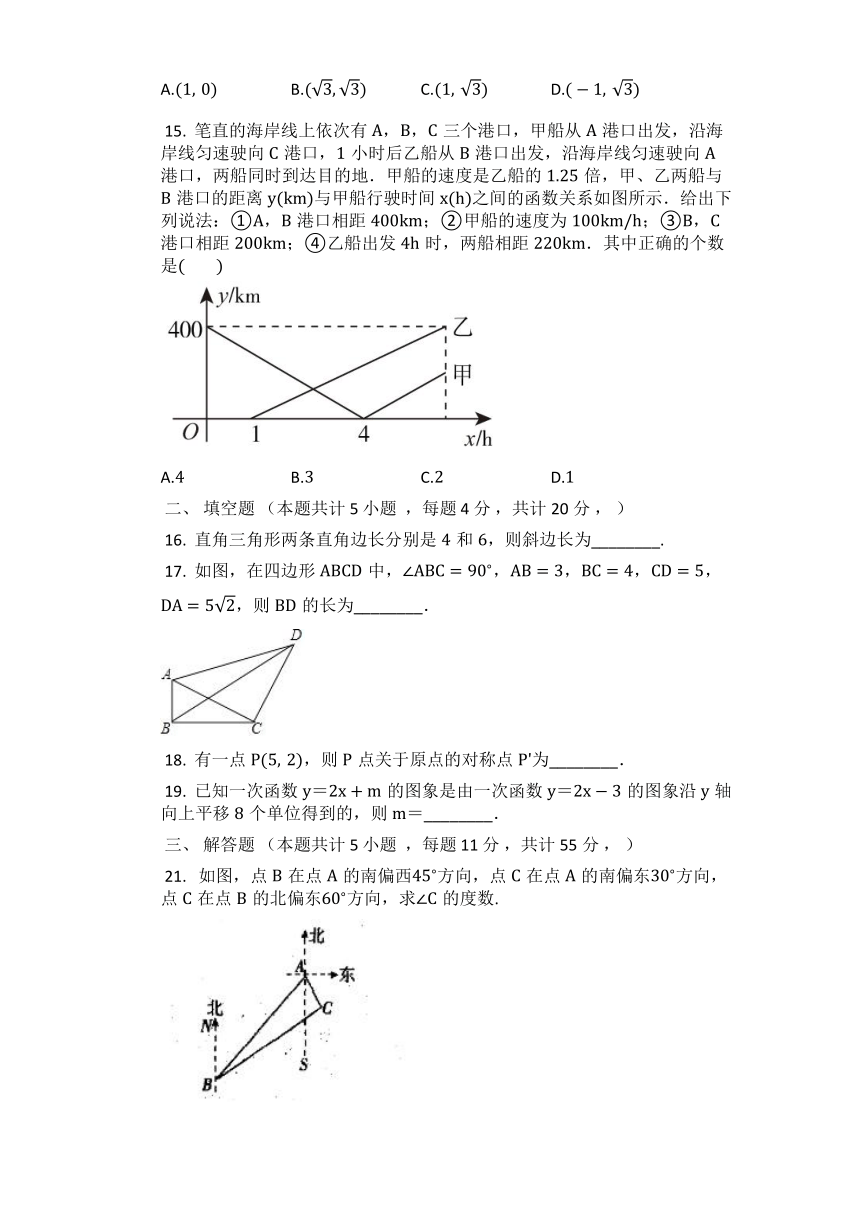
?15. 笔直的海岸线上依次有A,B,C三个港口,甲船从A港口出发,沿海岸线匀速驶向C港口,1小时后乙船从B港口出发,沿海岸线匀速驶向A港口,两船同时到达目的地.甲船的速度是乙船的1.25倍,甲、乙两船与B港口的距离y(km)与甲船行驶时间x(h)之间的函数关系如图所示.给出下列说法:①A,B港口相距400km;②甲船的速度为100km/h;③B,C港口相距200km;④乙船出发4h时,两船相距220km.其中正确的个数是(? ? ????)
A.4 B.3 C.2 D.1
二、 填空题 (本题共计 5 小题 ,每题 4 分 ,共计20分 , )
?16. 直角三角形两条直角边长分别是4和6,则斜边长为________.
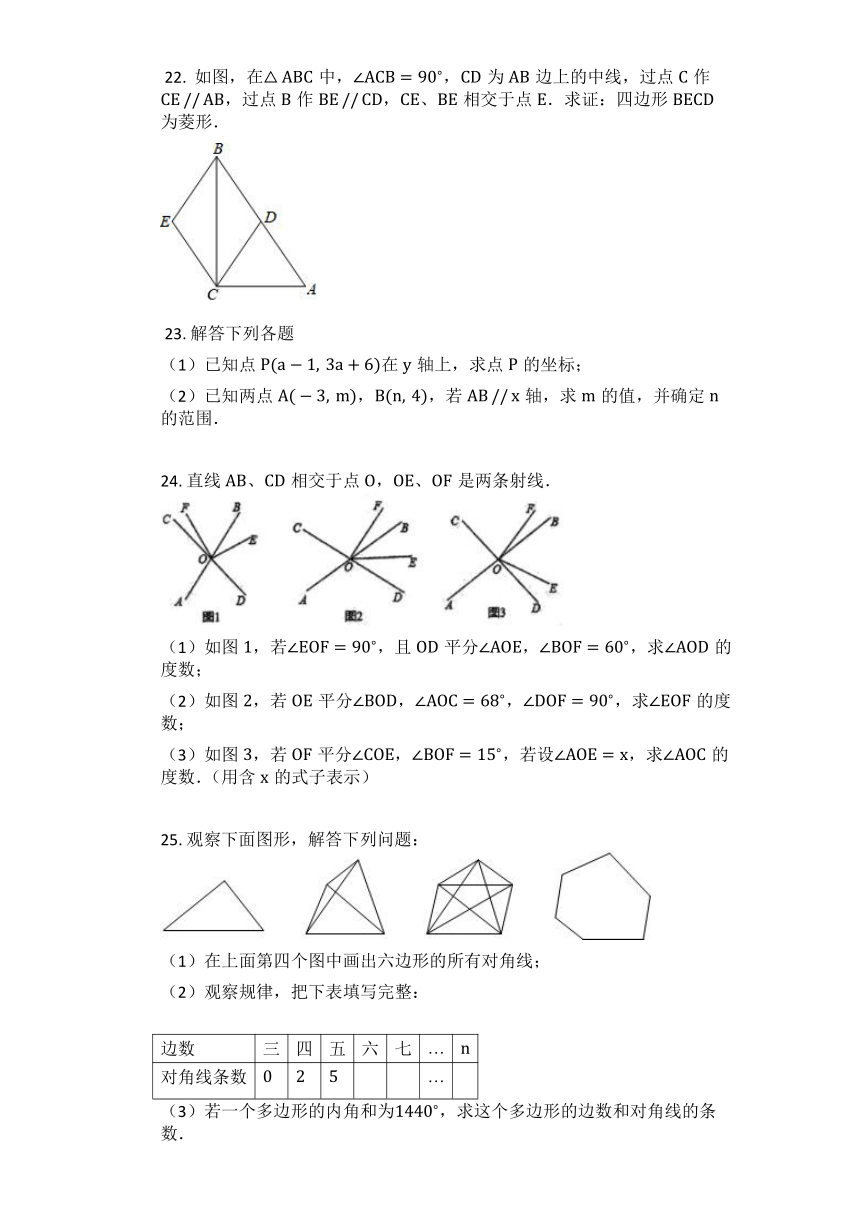
?17. 如图,在四边形ABCD中,∠ABC=90?,AB=3,BC=4,CD=5,DA=52,则BD的长为________.
?18. 有一点P(5,?2),则P点关于原点的对称点P'为________.
?19. 已知一次函数y=2x+m的图象是由一次函数y=2x?3的图象沿y轴向上平移8个单位得到的,则m=________.
三、 解答题 (本题共计 5 小题 ,每题 11 分 ,共计55分 , )
?21. ?如图,点B在点A的南偏西45?方向,点C在点A的南偏东30?方向,点C在点B的北偏东60?方向,求∠C的度数.
?22. 如图,在△ABC中,∠ACB=90?,CD为AB边上的中线,过点C作CE?//?AB,过点B作BE?//?CD,CE、BE相交于点E.求证:四边形BECD为菱形.
?23. 解答下列各题
(1)已知点P(a?1,?3a+6)在y轴上,求点P的坐标;
(2)已知两点A(?3,?m),B(n,?4),若AB?//?x轴,求m的值,并确定n的范围.
?
24. 直线AB、CD相交于点O,OE、OF是两条射线.
(1)如图1,若∠EOF=90?,且OD平分∠AOE,∠BOF=60?,求∠AOD的度数;
(2)如图2,若OE平分∠BOD,∠AOC=68?,∠DOF=90?,求∠EOF的度数;
(3)如图3,若OF平分∠COE,∠BOF=15?,若设∠AOE=x,求∠AOC的度数.(用含x的式子表示)
?
25. 观察下面图形,解答下列问题:
(1)在上面第四个图中画出六边形的所有对角线;
(2)观察规律,把下表填写完整:
边数
三
四
五
六
七
…
n
对角线条数
0
2
5
…
(3)若一个多边形的内角和为1440?,求这个多边形的边数和对角线的条数.
参考答案与试题解析
一、 选择题 (本题共计 15 小题 ,每题 3 分 ,共计45分 )
1.
【答案】
B
【解答】
A.82+122+172,不能构成直角三角形.故选项错误;
B.62+82=102,能构成直角三角形.故选项正确;
C.12+22≠32,不能构成直角三角形.故选项错误;
D.52+92≠122,不能构成直角三角形.故选项错误.
故选B.
2.
【答案】
D
【解答】
解:①当6和8均为直角边时,斜边=10,
则斜边上的中线=5;
②当6为直角边,8为斜边时,
则斜边上的中线=4.
故斜边上的中线长为:4或5.
故选:D.
3.
【答案】
B
【解答】
解:如图,取BC的中点G,连接EG,
∵ E是AC的中点,
∴ EG是△ABC的中位线,
∴ EG//AB,EG=12AB,
∵ AB=8,
∴ EG=4,
∵ CG=12BC,CD=12BC,EF=2CD,
∴ EF=CD,
∴ 四边形EGDF是平行四边形,
∴ DF=EG=4.
故选B.
4.
【答案】
D
【解答】
解:∵ 四边形ABCD是平行四边形,
∴ AB?//?CD,AB=CD,∠BCD=∠BAD=120?,
∵ AE?//?BD,
∴ 四边形ABDE是平行四边形,
∴ AB=DE,
∴ CE=2AB,
∵ ∠BCD=120?,
∴ ∠ECF=60?,
∵ EF⊥BC,
∴ ∠CEF=30?,
∴ CE=2CF=2,
∴ AB=1.
故选D.
5.
【答案】
C
【解答】
此题暂无解答
6.
【答案】
C
【解答】
解:设AE=x.
∵ 四边形ABCD是菱形,OC=2,∴ AC=4,
∵ CE⊥AB,BE=7,∴ BC=7+x,
根据勾股定理可得CE2=BC2?BE2=AC2?AE2,
∴ 7+x2?72=42?x2,
解得x1=1,x2=?8(舍去),
∴ BC=8,CE=82?72=15,
∴ S菱形ABCD=CE?AB=815.
故选C.
7.
【答案】
A
【解答】
解:∵ 点A(1,?2),AC⊥x轴,
∴ 点C的横坐标为1,
∵ AC⊥x轴,垂足为C,
∴ 点C的纵坐标为0,
∴ C(1,?0),
故选A.
8.
【答案】
A
【解答】
解:A不是中心对称图形,故本选项正确;
B是中心对称图形,故本选项错误;
C是中心对称图形,故本选项错误;
D是中心对称图形,故本选项错误.
故选A.
9.
【答案】
C
【解答】
解:根据题意得,x?1≥0且3?x>0,
解得x≥1且x<3,
所以,1≤x<3.
故选C.
10.
【答案】
A
【解答】
解:∵ 当x=?1时,y=?5×(?1)+1=?6≠5,
∴ 此点不在一次函数的图象上,
故①错误;
∵ k=?5<0,b=1>0,
∴ 此函数的图象经过一、二、四象限,
故②错误;
∵ x=1时,y=?5×1+1=?4,
又k=?5<0,
∴ y随x的增大而减小,
∴ 当x>1时,y故③错误,④错误.
故选:A.
11.
【答案】
B
【解答】
解:∵ y与x?1成正比例,
∴ y=k(x?1)(k≠0),
当x=1时,y=0,与k值无关,
∴ 直线y=k(x?1)经过定点(1,?0),
∵ 点(a,?a)(a≠0),
∴ 点(a,?a)在第一三象限的平分线上,
∴ 直线的大致图象为B选项图象.
故选B.
12.
【答案】
B
【解答】
解:∵ 最大值与最小值的差为:169?143=26,
∴ 组数=26÷5=5.2,
∴ 组数为6组.
故选B.
13.
【答案】
B
【解答】
解:依题意得:n+3=km+k+12n?1=km+k+k+1
∵k=0?4
00∴4故答案为:B.
14.
【答案】
C
【解答】
∵ A(?1,?0),
∴ OA=1,
在Rt△AOB中,∵ ∠AOB=90?,∠BAO=60?,OA=1,
∴ OB=3OA=3,
平移后,OC=1,CB'=OB=3,
∴ B'(1,?3),
15.
【答案】
B
【解答】
解:由题意知A,B港口相距400km,故①正确;
甲船4个小时行驶了400km,
故甲船的速度为400÷4=100km/h,故②正确;
乙船的速度为100÷1.25=80km/h,
设B,C港口的距离为skm,
则400÷80=400+s÷100?1,
解得s=200,故③正确;
乙船出发4h时,两船的距离为:
4×80+4+1?4×100=420km,故④错误,
综上,正确的有①②③,共3个.
故选B.
二、 填空题 (本题共计 5 小题 ,每题 4 分 ,共计20分 )
16.
【答案】
213
【解答】
解:∵ 直角三角形两条直角边长分别是4和6,
∴ 根据勾股定理得,其斜边长为:42+62=52=213.
故答案为:213.
17.
【答案】
65
【解答】
解:作DM⊥BC,交BC延长线于M,如图所示:
则∠M=90?
∠DCM+∠CDM=90?
∠ABC=90??AB=3,BC=4
AC2=AB2+BC2=25
AC=5
AD=52,CD=5
AC2+CD2=AD2
∴ACD是直角三角形,∠ACD=90?
∠ACB+∠DCM=90?
∠ACB=∠CDM
∠ABC=∠M=90?
∴ABC==CMD
ABCM=ACCD=55=1
CM=AB=3,DM=BC=4
BM=BC+CM=7
BD=BM2+DM2=72+42=65
故答案为:65
18.
【答案】
(?5,??2)
【解答】
解:∵ 点P(5,?2),
∴ P点关于原点的对称点P'为(?5,??2),
故答案为:(?5,??2).
19.
【答案】
5
【解答】
此题暂无解答
三、 解答题 (本题共计 5 小题 ,每题 11 分 ,共计55分 )
21.
【答案】
?解:如图,
根据题意,得
∠BAE=45?,∠CAE=30?,∠DBC=60?,
∴ ∠BAC=∠BAE+∠CAE
=45?+30?
=75?.
∵ AE?//?DB,
∴ ∠DBA=∠BAE=45?,
∴ ∠ABC=∠DBC?∠DBA
=60??45?
=15?,
∴ ∠ACB=180??∠ABC?∠BAC
=180??15??75?
=90?.
即∠C为:90?.
【解答】
?解:如图,
根据题意,得
∠BAE=45?,∠CAE=30?,∠DBC=60?,
∴ ∠BAC=∠BAE+∠CAE
=45?+30?
=75?.
∵ AE?//?DB,
∴ ∠DBA=∠BAE=45?,
∴ ∠ABC=∠DBC?∠DBA
=60??45?
=15?,
∴ ∠ACB=180??∠ABC?∠BAC
=180??15??75?
=90?.
即∠C为:90?.
22.
【答案】
证明:∵ CE?//?AB,BE?//?CD,
∴ 四边形BECD是平行四边形.
又∵ ∠ACB=90?,CD为AB边上的中线,
∴ CD=12AB=BD.
即BD=CD.
∴ 平行四边形BECD是菱形.
【解答】
证明:∵ CE?//?AB,BE?//?CD,
∴ 四边形BECD是平行四边形.
又∵ ∠ACB=90?,CD为AB边上的中线,
∴ CD=12AB=BD.
即BD=CD.
∴ 平行四边形BECD是菱形.
23.
【答案】
解:(1)∵ 点P在y轴上,
∴ a?1=0,即a=1,
∴ 点P坐标为(0,?9);
(2)∵ 两点A(?3,?m),B(n,?4),且AB?//?x轴,
∴ m=4,n≠?3.
【解答】
解:(1)∵ 点P在y轴上,
∴ a?1=0,即a=1,
∴ 点P坐标为(0,?9);
(2)∵ 两点A(?3,?m),B(n,?4),且AB?//?x轴,
∴ m=4,n≠?3.
24.
【答案】
解:(1)∵ ∠EOF=90?,∠BOF=60?,
∴ ∠BOE=30?,
∴∠AOE=150?,
∵ OD平分∠AOE,
∴ ∠AOD=∠EOD=75?.
(2)∠BOD=∠AOC=68?,
∵ OE平分∠BOD,
∴∠BOE=∠DOE=34?,
∵ ∠DOF=90?,
∴∠EOF=∠DOF?∠DOE=56?.
(3)设 ∠AOE=x,
则∠BOE=180??x,
∴ ∠EOF=15?+180??x=195??x,
∵ OF平分 ∠COE,
∴ ∠COF=∠EOF=195??x,
∴ ∠AOC=180??195??x?15?=x?30?.
【解答】
解:(1)∵ ∠EOF=90?,∠BOF=60?,
∴ ∠BOE=30?,
∴∠AOE=150?,
∵ OD平分∠AOE,
∴ ∠AOD=∠EOD=75?.
(2)∠BOD=∠AOC=68?,
∵ OE平分∠BOD,
∴∠BOE=∠DOE=34?,
∵ ∠DOF=90?,
∴∠EOF=∠DOF?∠DOE=56?.
(3)设?∠AOE=x,
则∠BOE=180??x,
∴ ∠EOF=15?+180??x=195??x,
∵ OF平分?∠COE,
∴ ∠COF=∠EOF=195??x,
∴ ∠AOC=180??195??x?15?=x?30?.
25.
【答案】
解:(1);
(2)
边数
三
四
五
六
七
…
n
对角线条数
0
2
5
9
14
…
?n(n?3)2
(3)设多边形的边数为n.
则(n?2)×180=1440,
解得n=10.
∴ 对角线的条数为:10×(10?3)2=35(条).
【解答】
解:(1);
(2)
边数
三
四
五
六
七
…
n
对角线条数
0
2
5
9
14
…
?n(n?3)2
(3)设多边形的边数为n.
则(n?2)×180=1440,
解得n=10.
∴ 对角线的条数为:10×(10?3)2=35(条).
班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 15 小题 ,每题 3 分 ,共计45分 , )
?1. 以下列各组数为三角形的边长,能构成直角三角形的是(???)
A.8,12,17; B.6,8,10; C.1,2,3; D.5,12,9
?2. 已知直角三角形的两边分别为6和8,则斜边上的中线长为( )
A.20 B.5 C.4 D.4或5
?3. 如图,在△ABC中,延长BC至D,使得CD=12BC,过AC中点E作EF//CD?(点F位于点E右侧),且EF=2CD,连接DF,若AB=8,则DF的长为(? ? ? ? )?
A.3 B.4 C.23 D.32
?4. 如图所示,在?ABCD中,∠BAD=120?,连接BD,作AE?//?BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是(? ? ? ? )
A.2 B.3 C.2 D.1
?5. 在?ABCD中,AB⊥AC,∠B=60?,AC=2falsecm,则?ABCD的周长是( )
A.10cm B.11cm C.12cm D.13cm
?6. 如图,在菱形ABCD中,AC与BD相交于点O,CE⊥AB,若OC=2,BE=7,则菱形ABCD的面积为(????????)
A.813 B.613 C.815 D.615
?7. 已知点A(1,?2),AC⊥x轴,垂足为C,则点C的坐标为( )
A.(1,?0) B.(0,?1) C.(2,?0) D.(0,?2)
?
8. 下列选项中的图形,不属于中心对称图形的是 (????????)
A.等边三角形 B.正方形 C.正六边形 D.圆
?9. 函数y=x?13?x的自变量x的取值范围是( )
A.1≤x≤3 B.1
①它的图象必经过点(?1,?5);②它的图象经过第一、二、三象限;③当x>1时,y<0;④y的值随x值的增大而增大.
其中正确的个数是( )
A.0 B.1 C.2 D.3
?11. 已知y是x的函数,y与x?1成正比例,如果这个函数的图象经过点(a,?a)(a≠0),那么它的图象大致是( )
A. B. C. D.
?12. 对某中学70名女生进行测量,得到一组数据的最大值169cm,最小值143cm,对这组数据整理时测定它的组距5cm,应分组数( )
A.5组 B.6组 C.7组 D.8组
?13. 若直线y=kx+k+1经过点(m,?n+3)和(m+1,?2n?1),且0
?14. 如图,平面直角坐标系中放置一个直角三角板OAB,∠OAB=60?,顶点A的坐标为(?1,?0),现将该三角板向右平移使点A与点O重合,得到△OCB',则点B的对应点B'的坐标是( )
A.(1,?0) B.(3,3) C.(1,?3) D.(?1,?3)
?15. 笔直的海岸线上依次有A,B,C三个港口,甲船从A港口出发,沿海岸线匀速驶向C港口,1小时后乙船从B港口出发,沿海岸线匀速驶向A港口,两船同时到达目的地.甲船的速度是乙船的1.25倍,甲、乙两船与B港口的距离y(km)与甲船行驶时间x(h)之间的函数关系如图所示.给出下列说法:①A,B港口相距400km;②甲船的速度为100km/h;③B,C港口相距200km;④乙船出发4h时,两船相距220km.其中正确的个数是(? ? ????)
A.4 B.3 C.2 D.1
二、 填空题 (本题共计 5 小题 ,每题 4 分 ,共计20分 , )
?16. 直角三角形两条直角边长分别是4和6,则斜边长为________.
?17. 如图,在四边形ABCD中,∠ABC=90?,AB=3,BC=4,CD=5,DA=52,则BD的长为________.
?18. 有一点P(5,?2),则P点关于原点的对称点P'为________.
?19. 已知一次函数y=2x+m的图象是由一次函数y=2x?3的图象沿y轴向上平移8个单位得到的,则m=________.
三、 解答题 (本题共计 5 小题 ,每题 11 分 ,共计55分 , )
?21. ?如图,点B在点A的南偏西45?方向,点C在点A的南偏东30?方向,点C在点B的北偏东60?方向,求∠C的度数.
?22. 如图,在△ABC中,∠ACB=90?,CD为AB边上的中线,过点C作CE?//?AB,过点B作BE?//?CD,CE、BE相交于点E.求证:四边形BECD为菱形.
?23. 解答下列各题
(1)已知点P(a?1,?3a+6)在y轴上,求点P的坐标;
(2)已知两点A(?3,?m),B(n,?4),若AB?//?x轴,求m的值,并确定n的范围.
?
24. 直线AB、CD相交于点O,OE、OF是两条射线.
(1)如图1,若∠EOF=90?,且OD平分∠AOE,∠BOF=60?,求∠AOD的度数;
(2)如图2,若OE平分∠BOD,∠AOC=68?,∠DOF=90?,求∠EOF的度数;
(3)如图3,若OF平分∠COE,∠BOF=15?,若设∠AOE=x,求∠AOC的度数.(用含x的式子表示)
?
25. 观察下面图形,解答下列问题:
(1)在上面第四个图中画出六边形的所有对角线;
(2)观察规律,把下表填写完整:
边数
三
四
五
六
七
…
n
对角线条数
0
2
5
…
(3)若一个多边形的内角和为1440?,求这个多边形的边数和对角线的条数.
参考答案与试题解析
一、 选择题 (本题共计 15 小题 ,每题 3 分 ,共计45分 )
1.
【答案】
B
【解答】
A.82+122+172,不能构成直角三角形.故选项错误;
B.62+82=102,能构成直角三角形.故选项正确;
C.12+22≠32,不能构成直角三角形.故选项错误;
D.52+92≠122,不能构成直角三角形.故选项错误.
故选B.
2.
【答案】
D
【解答】
解:①当6和8均为直角边时,斜边=10,
则斜边上的中线=5;
②当6为直角边,8为斜边时,
则斜边上的中线=4.
故斜边上的中线长为:4或5.
故选:D.
3.
【答案】
B
【解答】
解:如图,取BC的中点G,连接EG,
∵ E是AC的中点,
∴ EG是△ABC的中位线,
∴ EG//AB,EG=12AB,
∵ AB=8,
∴ EG=4,
∵ CG=12BC,CD=12BC,EF=2CD,
∴ EF=CD,
∴ 四边形EGDF是平行四边形,
∴ DF=EG=4.
故选B.
4.
【答案】
D
【解答】
解:∵ 四边形ABCD是平行四边形,
∴ AB?//?CD,AB=CD,∠BCD=∠BAD=120?,
∵ AE?//?BD,
∴ 四边形ABDE是平行四边形,
∴ AB=DE,
∴ CE=2AB,
∵ ∠BCD=120?,
∴ ∠ECF=60?,
∵ EF⊥BC,
∴ ∠CEF=30?,
∴ CE=2CF=2,
∴ AB=1.
故选D.
5.
【答案】
C
【解答】
此题暂无解答
6.
【答案】
C
【解答】
解:设AE=x.
∵ 四边形ABCD是菱形,OC=2,∴ AC=4,
∵ CE⊥AB,BE=7,∴ BC=7+x,
根据勾股定理可得CE2=BC2?BE2=AC2?AE2,
∴ 7+x2?72=42?x2,
解得x1=1,x2=?8(舍去),
∴ BC=8,CE=82?72=15,
∴ S菱形ABCD=CE?AB=815.
故选C.
7.
【答案】
A
【解答】
解:∵ 点A(1,?2),AC⊥x轴,
∴ 点C的横坐标为1,
∵ AC⊥x轴,垂足为C,
∴ 点C的纵坐标为0,
∴ C(1,?0),
故选A.
8.
【答案】
A
【解答】
解:A不是中心对称图形,故本选项正确;
B是中心对称图形,故本选项错误;
C是中心对称图形,故本选项错误;
D是中心对称图形,故本选项错误.
故选A.
9.
【答案】
C
【解答】
解:根据题意得,x?1≥0且3?x>0,
解得x≥1且x<3,
所以,1≤x<3.
故选C.
10.
【答案】
A
【解答】
解:∵ 当x=?1时,y=?5×(?1)+1=?6≠5,
∴ 此点不在一次函数的图象上,
故①错误;
∵ k=?5<0,b=1>0,
∴ 此函数的图象经过一、二、四象限,
故②错误;
∵ x=1时,y=?5×1+1=?4,
又k=?5<0,
∴ y随x的增大而减小,
∴ 当x>1时,y故③错误,④错误.
故选:A.
11.
【答案】
B
【解答】
解:∵ y与x?1成正比例,
∴ y=k(x?1)(k≠0),
当x=1时,y=0,与k值无关,
∴ 直线y=k(x?1)经过定点(1,?0),
∵ 点(a,?a)(a≠0),
∴ 点(a,?a)在第一三象限的平分线上,
∴ 直线的大致图象为B选项图象.
故选B.
12.
【答案】
B
【解答】
解:∵ 最大值与最小值的差为:169?143=26,
∴ 组数=26÷5=5.2,
∴ 组数为6组.
故选B.
13.
【答案】
B
【解答】
解:依题意得:n+3=km+k+12n?1=km+k+k+1
∵k=0?4
0
14.
【答案】
C
【解答】
∵ A(?1,?0),
∴ OA=1,
在Rt△AOB中,∵ ∠AOB=90?,∠BAO=60?,OA=1,
∴ OB=3OA=3,
平移后,OC=1,CB'=OB=3,
∴ B'(1,?3),
15.
【答案】
B
【解答】
解:由题意知A,B港口相距400km,故①正确;
甲船4个小时行驶了400km,
故甲船的速度为400÷4=100km/h,故②正确;
乙船的速度为100÷1.25=80km/h,
设B,C港口的距离为skm,
则400÷80=400+s÷100?1,
解得s=200,故③正确;
乙船出发4h时,两船的距离为:
4×80+4+1?4×100=420km,故④错误,
综上,正确的有①②③,共3个.
故选B.
二、 填空题 (本题共计 5 小题 ,每题 4 分 ,共计20分 )
16.
【答案】
213
【解答】
解:∵ 直角三角形两条直角边长分别是4和6,
∴ 根据勾股定理得,其斜边长为:42+62=52=213.
故答案为:213.
17.
【答案】
65
【解答】
解:作DM⊥BC,交BC延长线于M,如图所示:
则∠M=90?
∠DCM+∠CDM=90?
∠ABC=90??AB=3,BC=4
AC2=AB2+BC2=25
AC=5
AD=52,CD=5
AC2+CD2=AD2
∴ACD是直角三角形,∠ACD=90?
∠ACB+∠DCM=90?
∠ACB=∠CDM
∠ABC=∠M=90?
∴ABC==CMD
ABCM=ACCD=55=1
CM=AB=3,DM=BC=4
BM=BC+CM=7
BD=BM2+DM2=72+42=65
故答案为:65
18.
【答案】
(?5,??2)
【解答】
解:∵ 点P(5,?2),
∴ P点关于原点的对称点P'为(?5,??2),
故答案为:(?5,??2).
19.
【答案】
5
【解答】
此题暂无解答
三、 解答题 (本题共计 5 小题 ,每题 11 分 ,共计55分 )
21.
【答案】
?解:如图,
根据题意,得
∠BAE=45?,∠CAE=30?,∠DBC=60?,
∴ ∠BAC=∠BAE+∠CAE
=45?+30?
=75?.
∵ AE?//?DB,
∴ ∠DBA=∠BAE=45?,
∴ ∠ABC=∠DBC?∠DBA
=60??45?
=15?,
∴ ∠ACB=180??∠ABC?∠BAC
=180??15??75?
=90?.
即∠C为:90?.
【解答】
?解:如图,
根据题意,得
∠BAE=45?,∠CAE=30?,∠DBC=60?,
∴ ∠BAC=∠BAE+∠CAE
=45?+30?
=75?.
∵ AE?//?DB,
∴ ∠DBA=∠BAE=45?,
∴ ∠ABC=∠DBC?∠DBA
=60??45?
=15?,
∴ ∠ACB=180??∠ABC?∠BAC
=180??15??75?
=90?.
即∠C为:90?.
22.
【答案】
证明:∵ CE?//?AB,BE?//?CD,
∴ 四边形BECD是平行四边形.
又∵ ∠ACB=90?,CD为AB边上的中线,
∴ CD=12AB=BD.
即BD=CD.
∴ 平行四边形BECD是菱形.
【解答】
证明:∵ CE?//?AB,BE?//?CD,
∴ 四边形BECD是平行四边形.
又∵ ∠ACB=90?,CD为AB边上的中线,
∴ CD=12AB=BD.
即BD=CD.
∴ 平行四边形BECD是菱形.
23.
【答案】
解:(1)∵ 点P在y轴上,
∴ a?1=0,即a=1,
∴ 点P坐标为(0,?9);
(2)∵ 两点A(?3,?m),B(n,?4),且AB?//?x轴,
∴ m=4,n≠?3.
【解答】
解:(1)∵ 点P在y轴上,
∴ a?1=0,即a=1,
∴ 点P坐标为(0,?9);
(2)∵ 两点A(?3,?m),B(n,?4),且AB?//?x轴,
∴ m=4,n≠?3.
24.
【答案】
解:(1)∵ ∠EOF=90?,∠BOF=60?,
∴ ∠BOE=30?,
∴∠AOE=150?,
∵ OD平分∠AOE,
∴ ∠AOD=∠EOD=75?.
(2)∠BOD=∠AOC=68?,
∵ OE平分∠BOD,
∴∠BOE=∠DOE=34?,
∵ ∠DOF=90?,
∴∠EOF=∠DOF?∠DOE=56?.
(3)设 ∠AOE=x,
则∠BOE=180??x,
∴ ∠EOF=15?+180??x=195??x,
∵ OF平分 ∠COE,
∴ ∠COF=∠EOF=195??x,
∴ ∠AOC=180??195??x?15?=x?30?.
【解答】
解:(1)∵ ∠EOF=90?,∠BOF=60?,
∴ ∠BOE=30?,
∴∠AOE=150?,
∵ OD平分∠AOE,
∴ ∠AOD=∠EOD=75?.
(2)∠BOD=∠AOC=68?,
∵ OE平分∠BOD,
∴∠BOE=∠DOE=34?,
∵ ∠DOF=90?,
∴∠EOF=∠DOF?∠DOE=56?.
(3)设?∠AOE=x,
则∠BOE=180??x,
∴ ∠EOF=15?+180??x=195??x,
∵ OF平分?∠COE,
∴ ∠COF=∠EOF=195??x,
∴ ∠AOC=180??195??x?15?=x?30?.
25.
【答案】
解:(1);
(2)
边数
三
四
五
六
七
…
n
对角线条数
0
2
5
9
14
…
?n(n?3)2
(3)设多边形的边数为n.
则(n?2)×180=1440,
解得n=10.
∴ 对角线的条数为:10×(10?3)2=35(条).
【解答】
解:(1);
(2)
边数
三
四
五
六
七
…
n
对角线条数
0
2
5
9
14
…
?n(n?3)2
(3)设多边形的边数为n.
则(n?2)×180=1440,
解得n=10.
∴ 对角线的条数为:10×(10?3)2=35(条).
同课章节目录
