人教版A高中数学必修1课件-3.1.1方程的根与函数的零点(共51张PPT)
文档属性
| 名称 | 人教版A高中数学必修1课件-3.1.1方程的根与函数的零点(共51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-27 00:00:00 | ||
图片预览











文档简介
(共51张PPT)
互动课堂
2
随堂测评
3
预习导学
1
3.1.1方程的根与函数的零点
预习导学
●课标展示
1.理解函数零点的概念以及函数零点与方程根的关系.
2.会求函数的零点.
3.掌握函数零点存在的条件,并会判断函数零点的个数.
●温故知新
旧知再现
1.方程2x+1=0的根为x=________,函数y=2x+1与x轴的交点为__________
.
2.方程x2-2x-3=0的根为_______________
;函数y=x2-2x-3与x轴的交点为______________
.
3.函数y=2x2-8x+1的对称轴为______,顶点坐标为___________
.
x1=-1,x2=3
(-1,0),(3,0)
x=2
(2,-7)
新知导学
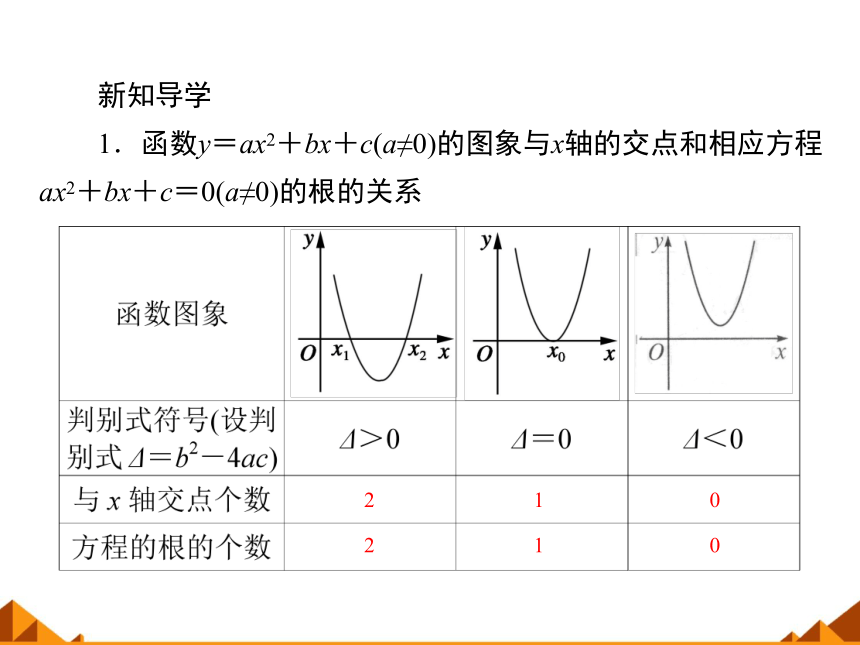
1.函数y=ax2+bx+c(a≠0)的图象与x轴的交点和相应方程ax2+bx+c=0(a≠0)的根的关系
2
1
0
2
1
0
2.函数的零点
(1)定义:对于函数y=f(x),我们把使__________成立的实数x叫做函数y=f(x)的零点.
(2)几何意义:函数y=f(x)的图象与____的交点的________就是函数y=f(x)的零点.
(3)结论:方程f(x)=0有________?函数y=f(x)的图象与x轴有_____?函数y=f(x)有_____.
[名师点拨] 并非所有的函数都有零点,例如,函数f(x)=x2+1,由于方程x2+1=0无实数根,故该函数无零点.
f(x)=0
x轴
横坐标
实数根
交点
零点
3.函数零点的判定定理
条件
结论
函数y=f(x)在[a,b]上
y=f(x)在(a,b)
内有零点
(1)图象是___________的曲线
(2)f(a)f(b)
_____0
连续不断
<
[名师点拨] 判断函数y=f(x)是否存在零点的方法:
(1)方程法:判断方程f(x)=0是否有实数解.
(2)图象法:判断函数y=f(x)的图象与x轴是否有交点.
(3)定理法:利用零点的判定定理来判断.
●自我检测
1.已知二次函数y=x2-x-1,则使y=0成立的实数x有( )
A.0个
B.1个
C.2个
D.无数个
[答案] C
[解析] 判别式Δ=1+4=5>0,则方程x2-x-1=0有两个不等式的实数根,即使y=0成立的实数x有2个.
2.已知函数y=f(x)有零点,下列说法不正确的是( )
A.f(0)=0
B.方程f(x)=0有实根
C.函数f(x)的图象与x轴有交点
D.函数f(x)的零点是方程f(x)=0的实数根
[答案] A
4.函数f(x)=x2+x-b2的零点个数是( )
A.0
B.1
C.2
D.无数
[答案] C
[解析] ∵一元二次方程x2+x-b2=0的根的判别式Δ=1+4b2>0,∴函数f(x)=x2+x-b2有2个零点.
5.函数f(x)=kx-2x在(0,1)上有零点,则实数k的取值范围是________.
[答案] (2,+∞)
[解析] f(0)=-1,f(1)=k-2,由于f(0)·f(1)<0,则-(k-2)<0,故k>2.
互动课堂
求下列函数的零点.
(1)f(x)=4x-3;
(2)f(x)=x2-3x+2;
(3)f(x)=2x;
(4)f(x)=log2(x+1).
[分析] 根据函数零点的定义,令y=0,解出定义域内的x就是零点.
求函数的零点
规律总结:
1.正确理解函数的零点:
(1)函数的零点是一个实数,当自变量取该值时,其函数值等于零.
(2)根据函数零点定义可知,函数f(x)的零点就是f(x)=0的根,因此判断一个函数是否有零点,有几个零点,就是判断方程f(x)=0是否有实根,有几个实根.即函数y=f(x)的零点?方程f(x)=0的实根?函数y=f(x)的图象与x轴交点的横坐标.
2.函数零点的求法:
(1)代数法:求方程f(x)=0的实数根.
(2)几何法:与函数y=f(x)的图象联系起来,图象与x轴的交点的横坐标即为函数的零点.
(1)指出下列函数的零点:
①f(x)=x2-2x-3零点为________.
②g(x)=lgx+2零点为________.
(2)已知-1和4是函数f(x)=ax2+bx-4的零点,则f(1)=________.
1
2
(2013~2014广东中山模拟)函数f(x)=ex+x-2的零点所在的一个区间是( )
A.(-2,-1)
B.(-1,0)
C.(0,1)
D.(1,2)
[分析] 函数零点附近函数值的符号相反,可据此求解.
判断函数零点所在的区间
2
[解析] 因为函数f(x)的图象是连续不断的一条曲线,又f(-2)=e-2-4<0,f(-1)=e-1-3<0,f(0)=-1<0,f(1)=e-1>0,f(2)=e2>0,所以f(0)·f(1)<0,故函数的零点所在的一个区间是(0,1).
[答案] C
规律总结:判断函数零点所在区间的方法
一般而言判断函数零点所在区间的方法是将区间端点代入函数求出函数的值,进行符号判断即可得出结论.此类问题的难点往往是函数值符号的判断,可运用函数的有关性质进行判断.
函数f(x)=lnx+2x-6的零点所在的一个区间是( )
A.(1,2)
B.(2,3)
C.(3,4)
D.(4,5)
[答案] B
[解析] 因为f(1)=ln1+2×1-6=-4<0,f(2)=ln2+2×2-6<ln
e2-2=0,f(3)=ln3+2×3-6=ln3>0,f(4)=ln4+2×4-6=2ln2+2>0,f(5)=ln5+2×5-6=ln5+4>0,所以f(2)·f(3)<0,又函数f(x)的图象是连续不断的一条曲线,故函数f(x)的零点所在的一个区间是(2,3).
求函数f(x)=2x+lg(x+1)-2的零点个数.
[分析]
函数零点个数的判断
[解析] 解法一:因为f(0)=1+0-2=-1<0,f(2)=4+lg3-2≈2.48>0,所以由函数零点存在性判定定理知,f(x)在(0,2)上必定存在零点.
又f(x)=2x+lg(x+1)-2在(-1,+∞)上为增函数,故f(x)=0有且只有一个实根,即函数f(x)仅有一个零点.
解法二:
在同一坐标系中作出h(x)=2-2x和g(x)=lg(x+1)的图象,如右图所示,由图象可知h(x)=2-2x和g(x)=lg(x+1)有且只有一个交点,即f(x)=2x+lg(x+1)-2与x轴有且只有一个交点,即函数f(x)仅有一个零点.
规律总结:判断函数零点个数的主要方法:
(1)利用方程根,转化为解方程,有几个根就有几个零点.
(2)画出函数y=f(x)的图象,判定它与x轴的交点个数,从而判定零点的个数.
(3)结合单调性,利用f(a)·f(b)<0,可判定y=f(x)在(a,b)上零点的个数.
(4)转化成两个函数图象的交点问题.
判断函数f(x)=x-3+lnx的零点的个数.
3
[解析] 解法一:在同一平面直角坐标系中画出函数y=lnx,y=-x+3的图象,如右图所示.
由图可知函数y=lnx,y=-x+3的图象只有一个交点,即函数f(x)=x-3+lnx只有一个零点.
●误区警示
易错点一 混淆了零点与点的概念
函数f(x)=x2-6x+5的零点是________.
[错解] (1,0),(5,0)
由题意,得x2-6x+5=0,∴x=1,x=5,
∴函数的零点是(1,0)和(5,0).
[错因分析] 该解法中混淆了零点与点的概念.
4
[思路分析] 零点不是一个点,而是函数图象与x轴交点的横坐标,零点是一值.
[正解] 1、5
由题意,得x2-6x+5=0,解得x=1或x=5,
∴函数的零点是1,5.
函数f(x)=x2-3x+2的零点是( )
A.(1,0)
B.(2,0)
C.(1,0),(2,0)
D.1,2
[错解] C
[错因分析] 错解的原因是没有理解零点的概念,“望文生义”,认为零点就是一个点.
1
[正解] 解方程x2-3x+2=0,得x=1或x=2,所以选D.
[总结] 函数的零点是一个实数,是使f(x)=0成立的实数x,也是函数y=f(x)的图象与x轴交点的横坐标.
易错点二 判断零点个数时出现逻辑错误
求函数f(x)=x2-5x+6在[1,4]上的零点个数.
[错解] 错解一:由题意,得f(1)=2>0,f(4)=2>0,因此函数f(x)=x2-5x+6在[1,4]上没有零点,即零点个数是0.
错解二:∵f(1)=2>0,f(2.5)=-0.25<0,∴函数在(1,2.5)内有一个零点;
又∵f(4)=2>0,f(2.5)=-0.25<0,∴函数在(2.5,4)内有一个零点,
∴函数在[1,4]上有两个零点.
5
[错因分析] 对于错解一,是错误地类比零点存在定理,f(a)·f(b)>0时,(a,b)中的零点情况是不确定的,而错解二出现了逻辑错误,当f(a)·f(b)<0时,(a,b)中存在零点,但个数不确定.
[思路分析] 要想准确地判断函数零点的个数,要么把它们全部求出来,要么利用函数图象来判断,这才是正确的方法.
[正解] 由题意,得x2-5x+6=0,
∴x=2,x=3,
∴函数的零点是2,3
∴函数在[1,4]上的零点的个数是2.
[错因分析] 由于f(x)在定义域内是大于等于0的,所以该题不宜用零点的存在性定理求解.
[总结] 当函数y=f(x)的图象在闭区间[a,b]上是一条连续不断的曲线,但是不满足f(a)·f(b)<0时,函数y=f(x)在区间(a,b)内可能存在零点,也可能不存在零点.
随堂测评
1.下列函数的图象中没有零点的是( )
[答案] D
[解析] 从图中观察知,只有D中函数图象与x轴没有交点,故选D.
[规律总结] 根据函数零点的概念,函数有零点,即函数的图象与x轴有交点.函数图象与x轴有几个交点,函数就有几个零点.
[答案] B
[解析] f(4)=-8+m=0,∴m=8,故选B.
[答案] A
[解析] 函数f(x)的定义域为{x|x≠0},
当x>0时,f(x)>0;
当x<0时,f(x)<0,
但此函数在定义域内的图象不连续,
所以函数没有零点,故选A.
[答案] B
[规律总结] 这是一类非常基础且常见的问题,考查的是函数零点的判定方法,一般而言只需将区间端点代入函数求出函数的值,进行符号判断即可得出结论.这类问题的难点往往是函数值符号的判断,可运用函数的有关性质进行判断.
5.函数f(x)为偶函数,其图象与x轴有四个交点,则该函数的所有零点之和为________.
[答案] 0
[解析] ∵y=f(x)为偶数,∴f(-x)=f(x),∴四个根之和为0.
[分析] 分别令各个解析式等于0,根据方程是否有根来确定函数的零点.
互动课堂
2
随堂测评
3
预习导学
1
3.1.1方程的根与函数的零点
预习导学
●课标展示
1.理解函数零点的概念以及函数零点与方程根的关系.
2.会求函数的零点.
3.掌握函数零点存在的条件,并会判断函数零点的个数.
●温故知新
旧知再现
1.方程2x+1=0的根为x=________,函数y=2x+1与x轴的交点为__________
.
2.方程x2-2x-3=0的根为_______________
;函数y=x2-2x-3与x轴的交点为______________
.
3.函数y=2x2-8x+1的对称轴为______,顶点坐标为___________
.
x1=-1,x2=3
(-1,0),(3,0)
x=2
(2,-7)
新知导学
1.函数y=ax2+bx+c(a≠0)的图象与x轴的交点和相应方程ax2+bx+c=0(a≠0)的根的关系
2
1
0
2
1
0
2.函数的零点
(1)定义:对于函数y=f(x),我们把使__________成立的实数x叫做函数y=f(x)的零点.
(2)几何意义:函数y=f(x)的图象与____的交点的________就是函数y=f(x)的零点.
(3)结论:方程f(x)=0有________?函数y=f(x)的图象与x轴有_____?函数y=f(x)有_____.
[名师点拨] 并非所有的函数都有零点,例如,函数f(x)=x2+1,由于方程x2+1=0无实数根,故该函数无零点.
f(x)=0
x轴
横坐标
实数根
交点
零点
3.函数零点的判定定理
条件
结论
函数y=f(x)在[a,b]上
y=f(x)在(a,b)
内有零点
(1)图象是___________的曲线
(2)f(a)f(b)
_____0
连续不断
<
[名师点拨] 判断函数y=f(x)是否存在零点的方法:
(1)方程法:判断方程f(x)=0是否有实数解.
(2)图象法:判断函数y=f(x)的图象与x轴是否有交点.
(3)定理法:利用零点的判定定理来判断.
●自我检测
1.已知二次函数y=x2-x-1,则使y=0成立的实数x有( )
A.0个
B.1个
C.2个
D.无数个
[答案] C
[解析] 判别式Δ=1+4=5>0,则方程x2-x-1=0有两个不等式的实数根,即使y=0成立的实数x有2个.
2.已知函数y=f(x)有零点,下列说法不正确的是( )
A.f(0)=0
B.方程f(x)=0有实根
C.函数f(x)的图象与x轴有交点
D.函数f(x)的零点是方程f(x)=0的实数根
[答案] A
4.函数f(x)=x2+x-b2的零点个数是( )
A.0
B.1
C.2
D.无数
[答案] C
[解析] ∵一元二次方程x2+x-b2=0的根的判别式Δ=1+4b2>0,∴函数f(x)=x2+x-b2有2个零点.
5.函数f(x)=kx-2x在(0,1)上有零点,则实数k的取值范围是________.
[答案] (2,+∞)
[解析] f(0)=-1,f(1)=k-2,由于f(0)·f(1)<0,则-(k-2)<0,故k>2.
互动课堂
求下列函数的零点.
(1)f(x)=4x-3;
(2)f(x)=x2-3x+2;
(3)f(x)=2x;
(4)f(x)=log2(x+1).
[分析] 根据函数零点的定义,令y=0,解出定义域内的x就是零点.
求函数的零点
规律总结:
1.正确理解函数的零点:
(1)函数的零点是一个实数,当自变量取该值时,其函数值等于零.
(2)根据函数零点定义可知,函数f(x)的零点就是f(x)=0的根,因此判断一个函数是否有零点,有几个零点,就是判断方程f(x)=0是否有实根,有几个实根.即函数y=f(x)的零点?方程f(x)=0的实根?函数y=f(x)的图象与x轴交点的横坐标.
2.函数零点的求法:
(1)代数法:求方程f(x)=0的实数根.
(2)几何法:与函数y=f(x)的图象联系起来,图象与x轴的交点的横坐标即为函数的零点.
(1)指出下列函数的零点:
①f(x)=x2-2x-3零点为________.
②g(x)=lgx+2零点为________.
(2)已知-1和4是函数f(x)=ax2+bx-4的零点,则f(1)=________.
1
2
(2013~2014广东中山模拟)函数f(x)=ex+x-2的零点所在的一个区间是( )
A.(-2,-1)
B.(-1,0)
C.(0,1)
D.(1,2)
[分析] 函数零点附近函数值的符号相反,可据此求解.
判断函数零点所在的区间
2
[解析] 因为函数f(x)的图象是连续不断的一条曲线,又f(-2)=e-2-4<0,f(-1)=e-1-3<0,f(0)=-1<0,f(1)=e-1>0,f(2)=e2>0,所以f(0)·f(1)<0,故函数的零点所在的一个区间是(0,1).
[答案] C
规律总结:判断函数零点所在区间的方法
一般而言判断函数零点所在区间的方法是将区间端点代入函数求出函数的值,进行符号判断即可得出结论.此类问题的难点往往是函数值符号的判断,可运用函数的有关性质进行判断.
函数f(x)=lnx+2x-6的零点所在的一个区间是( )
A.(1,2)
B.(2,3)
C.(3,4)
D.(4,5)
[答案] B
[解析] 因为f(1)=ln1+2×1-6=-4<0,f(2)=ln2+2×2-6<ln
e2-2=0,f(3)=ln3+2×3-6=ln3>0,f(4)=ln4+2×4-6=2ln2+2>0,f(5)=ln5+2×5-6=ln5+4>0,所以f(2)·f(3)<0,又函数f(x)的图象是连续不断的一条曲线,故函数f(x)的零点所在的一个区间是(2,3).
求函数f(x)=2x+lg(x+1)-2的零点个数.
[分析]
函数零点个数的判断
[解析] 解法一:因为f(0)=1+0-2=-1<0,f(2)=4+lg3-2≈2.48>0,所以由函数零点存在性判定定理知,f(x)在(0,2)上必定存在零点.
又f(x)=2x+lg(x+1)-2在(-1,+∞)上为增函数,故f(x)=0有且只有一个实根,即函数f(x)仅有一个零点.
解法二:
在同一坐标系中作出h(x)=2-2x和g(x)=lg(x+1)的图象,如右图所示,由图象可知h(x)=2-2x和g(x)=lg(x+1)有且只有一个交点,即f(x)=2x+lg(x+1)-2与x轴有且只有一个交点,即函数f(x)仅有一个零点.
规律总结:判断函数零点个数的主要方法:
(1)利用方程根,转化为解方程,有几个根就有几个零点.
(2)画出函数y=f(x)的图象,判定它与x轴的交点个数,从而判定零点的个数.
(3)结合单调性,利用f(a)·f(b)<0,可判定y=f(x)在(a,b)上零点的个数.
(4)转化成两个函数图象的交点问题.
判断函数f(x)=x-3+lnx的零点的个数.
3
[解析] 解法一:在同一平面直角坐标系中画出函数y=lnx,y=-x+3的图象,如右图所示.
由图可知函数y=lnx,y=-x+3的图象只有一个交点,即函数f(x)=x-3+lnx只有一个零点.
●误区警示
易错点一 混淆了零点与点的概念
函数f(x)=x2-6x+5的零点是________.
[错解] (1,0),(5,0)
由题意,得x2-6x+5=0,∴x=1,x=5,
∴函数的零点是(1,0)和(5,0).
[错因分析] 该解法中混淆了零点与点的概念.
4
[思路分析] 零点不是一个点,而是函数图象与x轴交点的横坐标,零点是一值.
[正解] 1、5
由题意,得x2-6x+5=0,解得x=1或x=5,
∴函数的零点是1,5.
函数f(x)=x2-3x+2的零点是( )
A.(1,0)
B.(2,0)
C.(1,0),(2,0)
D.1,2
[错解] C
[错因分析] 错解的原因是没有理解零点的概念,“望文生义”,认为零点就是一个点.
1
[正解] 解方程x2-3x+2=0,得x=1或x=2,所以选D.
[总结] 函数的零点是一个实数,是使f(x)=0成立的实数x,也是函数y=f(x)的图象与x轴交点的横坐标.
易错点二 判断零点个数时出现逻辑错误
求函数f(x)=x2-5x+6在[1,4]上的零点个数.
[错解] 错解一:由题意,得f(1)=2>0,f(4)=2>0,因此函数f(x)=x2-5x+6在[1,4]上没有零点,即零点个数是0.
错解二:∵f(1)=2>0,f(2.5)=-0.25<0,∴函数在(1,2.5)内有一个零点;
又∵f(4)=2>0,f(2.5)=-0.25<0,∴函数在(2.5,4)内有一个零点,
∴函数在[1,4]上有两个零点.
5
[错因分析] 对于错解一,是错误地类比零点存在定理,f(a)·f(b)>0时,(a,b)中的零点情况是不确定的,而错解二出现了逻辑错误,当f(a)·f(b)<0时,(a,b)中存在零点,但个数不确定.
[思路分析] 要想准确地判断函数零点的个数,要么把它们全部求出来,要么利用函数图象来判断,这才是正确的方法.
[正解] 由题意,得x2-5x+6=0,
∴x=2,x=3,
∴函数的零点是2,3
∴函数在[1,4]上的零点的个数是2.
[错因分析] 由于f(x)在定义域内是大于等于0的,所以该题不宜用零点的存在性定理求解.
[总结] 当函数y=f(x)的图象在闭区间[a,b]上是一条连续不断的曲线,但是不满足f(a)·f(b)<0时,函数y=f(x)在区间(a,b)内可能存在零点,也可能不存在零点.
随堂测评
1.下列函数的图象中没有零点的是( )
[答案] D
[解析] 从图中观察知,只有D中函数图象与x轴没有交点,故选D.
[规律总结] 根据函数零点的概念,函数有零点,即函数的图象与x轴有交点.函数图象与x轴有几个交点,函数就有几个零点.
[答案] B
[解析] f(4)=-8+m=0,∴m=8,故选B.
[答案] A
[解析] 函数f(x)的定义域为{x|x≠0},
当x>0时,f(x)>0;
当x<0时,f(x)<0,
但此函数在定义域内的图象不连续,
所以函数没有零点,故选A.
[答案] B
[规律总结] 这是一类非常基础且常见的问题,考查的是函数零点的判定方法,一般而言只需将区间端点代入函数求出函数的值,进行符号判断即可得出结论.这类问题的难点往往是函数值符号的判断,可运用函数的有关性质进行判断.
5.函数f(x)为偶函数,其图象与x轴有四个交点,则该函数的所有零点之和为________.
[答案] 0
[解析] ∵y=f(x)为偶数,∴f(-x)=f(x),∴四个根之和为0.
[分析] 分别令各个解析式等于0,根据方程是否有根来确定函数的零点.
