2020-2021学年人教五四新版六年级下册数学期末冲刺试题(word版含解析)
文档属性
| 名称 | 2020-2021学年人教五四新版六年级下册数学期末冲刺试题(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 00:00:00 | ||
图片预览



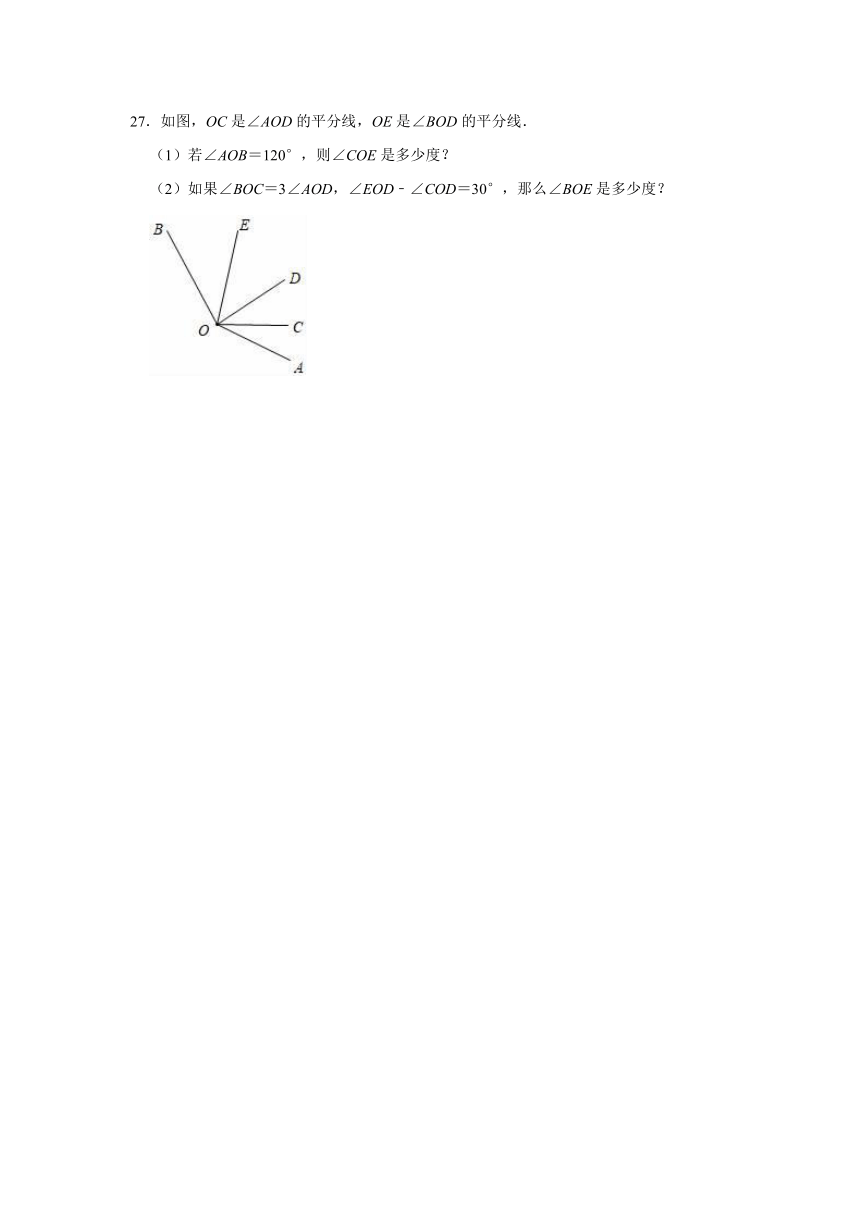
文档简介
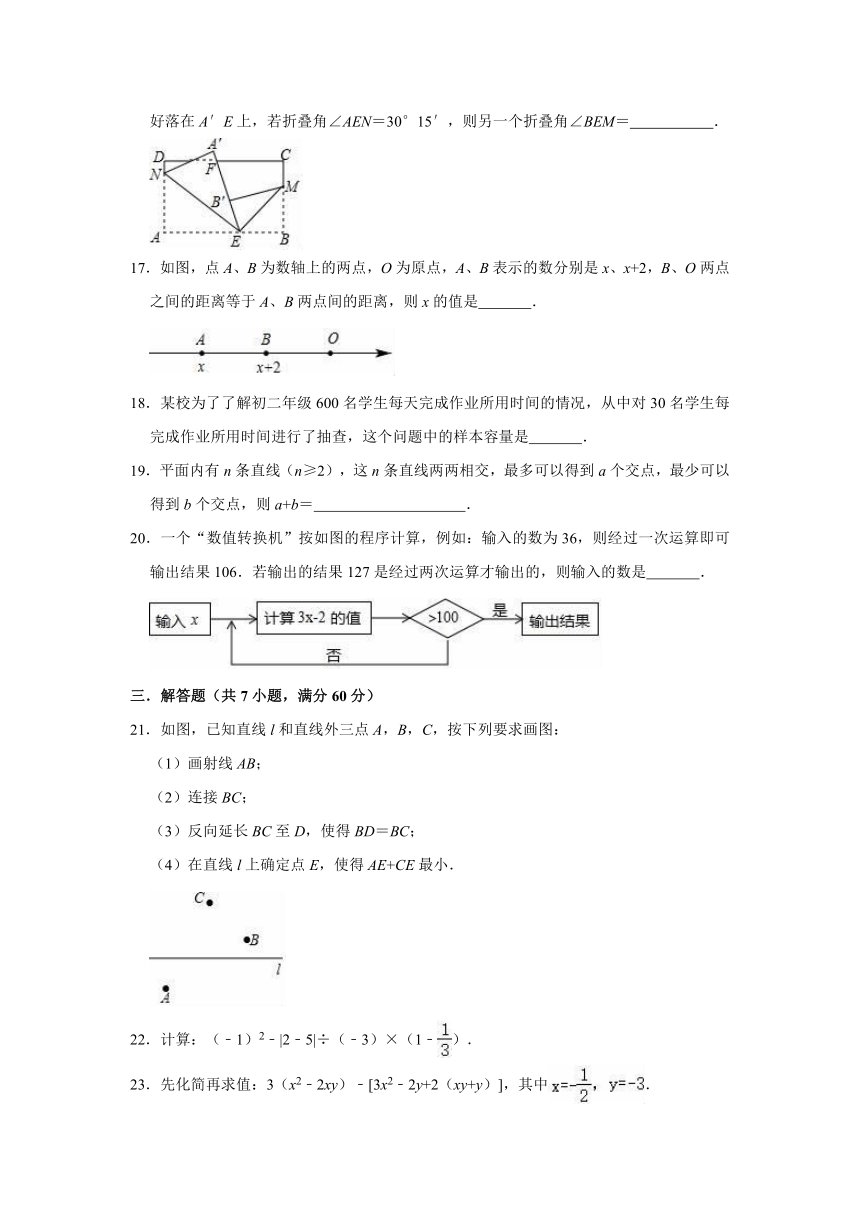
2020-2021学年人教五四新版六年级下册数学期末冲刺试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列各数中,数值最大的是( )
A.5:9
B.55%
C.0.555
D.
2.某一时刻,时钟上显示的时间是9点30分,则此时时针与分针的夹角是( )
A.75°
B.90°
C.105°
D.120°
3.下列调查中,最适合采用全面调查(普查)的是( )
A.对我市中学生近视情况的调查
B.对我市市民国庆出游情况的调查
C.对全国人民掌握新冠防疫知识情况的调查
D.对我国自行研制的大型飞机C919各零部件质量情况的调查
4.实数a、b、c、d在数轴上的对应点的位置如图所示,在这四个数中,绝对值最小的数是( )
A.a
B.b
C.c
D.d
5.在立方体六个面上,分别标上“我、爱、华、侨、中、学”,如图是立体的三种不同摆法,则三种摆法的左侧面上三个字分别是( )
A.爱、华、侨
B.爱、中、学
C.中、我、侨
D.中、学、侨
6.在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )
A.﹣54
B.54
C.﹣558
D.558
7.下列说法正确的是( )
A.4π是一次单项式
B.
+x﹣3是二次三项式
C.﹣的系数是﹣2
D.﹣x的系数是﹣1
8.今年我市有近3500名考生参加中考,为了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析,这个问题中样本是( )
A.每位考生的数学成绩
B.3500名考生的数学成绩
C.被抽取的800名考生的数学成绩
D.被抽取的800名学生
9.将34.945取近似数精确到十分位,正确的是( )
A.34.9
B.35.0
C.35
D.35.05
10.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图形有10个正三角形,…依此规律,若第n个图案有2020个三角形,则n=( )
A.670
B.672
C.673
D.676
二.填空题(共10小题,满分30分,每小题3分)
11.2020年6月23日,北斗三号最后一颗全球组网卫星从西昌发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为
.
12.如果﹣a=2,则a=
.
13.某班班主任把本班学生体育期末考试成绩绘制成扇形统计图,已知全班有40名学生,其中体育成绩优秀的有16人,则代表体育成绩优秀的扇形所对应的圆心角度数是
.
14.在90%,+8,0,﹣15,﹣0.7,+,19中正数有
个.
15.已知两个单项式3xym与﹣3xny2的和为0,则m+n的值是
.
16.如图,将长方形纸片ABCD沿直线EN、EM进行折叠后(点E在AB边上),B′点刚好落在A′E上,若折叠角∠AEN=30°15′,则另一个折叠角∠BEM=
.
17.如图,点A、B为数轴上的两点,O为原点,A、B表示的数分别是x、x+2,B、O两点之间的距离等于A、B两点间的距离,则x的值是
.
18.某校为了了解初二年级600名学生每天完成作业所用时间的情况,从中对30名学生每完成作业所用时间进行了抽查,这个问题中的样本容量是
.
19.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b=
.
20.一个“数值转换机”按如图的程序计算,例如:输入的数为36,则经过一次运算即可输出结果106.若输出的结果127是经过两次运算才输出的,则输入的数是
.
三.解答题(共7小题,满分60分)
21.如图,已知直线l和直线外三点A,B,C,按下列要求画图:
(1)画射线AB;
(2)连接BC;
(3)反向延长BC至D,使得BD=BC;
(4)在直线l上确定点E,使得AE+CE最小.
22.计算:(﹣1)2﹣|2﹣5|÷(﹣3)×(1﹣).
23.先化简再求值:3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)],其中.
24.为了解某校七年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组
频数
1.2≤x<1.6
a
1.6≤x<2.0
12
2.0≤x<2.4
b
2.4≤x<2.8
10
请根据图表中所提供的信息,完成下列问题:
(1)求a,b的值,并将频数分布直方图补充完整;
(2)该校七年级共有800名学生,估计该年级学生立定跳远成绩在1.6≤x<2.0范围内的学生有多少人?
25.如图,C,D是线段AB上的两点,已知M,N分别为AC,DB的中点,AB=18cm,且AC:CD:DB=1:2:3,求线段MN的长.
26.小明练习跳绳.以1分钟跳165个为目标,并把20次1分钟跳绳的数量记录如表(超过165个的部分记为“+”,少于165个的部分记为“﹣”)
与目标数量的差异(单位:个)
﹣11
﹣6
﹣2
+4
+10
次数
4
5
3
6
2
(1)小明在这20次跳绳练习中,1分钟最多跳多少个?
(2)小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多几个?
(3)小明在这20次跳绳练习中,累计跳绳多少个?
27.如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
(1)若∠AOB=120°,则∠COE是多少度?
(2)如果∠BOC=3∠AOD,∠EOD﹣∠COD=30°,那么∠BOE是多少度?
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:5:9=0.,
55%=0.55,
=0.6,
∵0.,0.55,0.555,0.6中0.6最大,
∴数值最大的是.
故选:D.
2.解:时针与分针相距3+=(份),
时钟面上的时针与分针的夹角是30°×=105°,
故选:C.
3.解:A、对我市中学生近视情况的调查,人数众多,应采用抽样调查,故此选项不合题意;
B、对我市市民国庆出游情况的调查,人数众多,应采用抽样调查,故此选项不合题意;
C、对全国人民掌握新冠防疫知识情况的调查,人数众多,应采用抽样调查,故此选项不合题意;
D、对我国自行研制的大型飞机C919各零部件质量情况的调查,意义重大,应采用全面调查,故此选项符合题意;
故选:D.
4.解:由图可知:c到原点O的距离最短,
所以在这四个数中,绝对值最小的数是c;
故选:C.
5.解:根据三个图形的汉字,可推断出来,和我相对的就是华.和侨相对的就是爱.和中相对的就是学.
∴三种摆法的左侧面上三个字分别是爱、中、学.
故选:B.
6.解:把x=2代入计算程序中得:(2﹣8)×9=﹣54,
把x=﹣54代入计算程序中得:(﹣54﹣8)×9=﹣558,
则输出结果为﹣558,
故选:C.
7.解:A、4π是数字,是零次单项式,不符合题意;
B、+x﹣3不是整式,不符合题意;
C、﹣的系数为﹣,不符合题意;
D、﹣x的系数是﹣1,符合题意,
故选:D.
8.解:A是个体,B是总体,C是样本,今年我市有近3500名考生参加中考,为了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析,这个问题中样本是抽取的800名考生的数学成绩为样本.
故选:C.
9.解:34.945取近似数精确到十分位是34.9;
故选:A.
10.解:∵第(1)个图案有3+1=4个三角形,
第(2)个图案有3×2+1=7个三角形,
第(3)个图案有3×3+1=10个三角形,
…
∴第n个图案有(3n+1)个三角形.
根据题意可得:3n+1=2020,
解得:n=673,
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:将36000用科学记数法表示应为3.6×104,
故答案为:3.6×104.
12.解:∵﹣a=2,
∴a=﹣2.
故答案为:2.
13.解:根据题意得360°×=144°,
故答案为:144°.
14.解:在90%,+8,0,﹣15,﹣0.7,+,19中正数有:
90%,+8,+,19,共有4个,
故答案为:4.
15.解:∵两个单项式3xym与﹣3xny2的和为0,
∴两个单项式是同类项,
即m=2,n=1,
∴m+n=3.
故答案为:3.
16.解:由折叠性质得:∠AEN=∠A′EN,∠BEM=∠B′EM,
∴∠A′EN=30°15′,
∠BEM=(180°﹣∠AEN﹣∠A′EN)=(180°﹣30°15′﹣30°15′)=59°45′,
故答案为:59°45′.
17.解:根据题意得:0﹣(x+2)=x+2﹣x,
解得:x=﹣4.
故答案为:﹣4.
18.解:∵某校为了了解初二年级600名学生每天完成作业所用时间的情况,从中对30名学生每完成作业所用时间进行了抽查,
∴这个问题中的样本容量是30.
故答案为:30.
19.解:如图:2条直线相交有1个交点,
3条直线相交有1+2个交点,
4条直线相交有1+2+3个交点,
5条直线相交有1+2+3+4个交点,
6条直线相交有1+2+3+4+5个交点,
…
n直线相交有个交点.
∴,而b=1,
∴
故答案为:.
20.解:根据题意得:3x﹣2=127,
解得:x=43,
可得3x﹣2=43,
解得:x=15,
则输入的数是15,
故答案为:15
三.解答题(共7小题,满分60分)
21.解:(1)射线AB,如图所示;
(2)线段BC,如图所示,
(3)线段BD如图所示
(4)点E即为所求;
22.解:(﹣1)2﹣|2﹣5|÷(﹣3)×(1﹣)
=1﹣3÷(﹣3)×
=1+3×
=1+
=.
23.解:原式=3x2﹣6xy﹣[3x2﹣2y+2xy+2y]
=3x2﹣6xy﹣(3x2+2xy)
=3x2﹣6xy﹣3x2﹣2xy
=﹣8xy
当时
原式=﹣8×(﹣)×(﹣3)=﹣12.
24.解:(1)由频数分布直方图可知,a=8,
b=50﹣8﹣12﹣10=20,
补全的频数分布直方图如右图所示;
(2)800×=192(人),
答:该年级学生立定跳远成绩在1.6≤x<2.0范围内的学生有192人.
25.解:设AC,CD,DB的长分别为xcm,2xcm,3xcm
∵AC+CD+DB=AB,AB=18cm
∴x+2x+3x=18
解得x=3
∴AC=3cm,CD=6cm,DB=9cm
∵M,N为AC,DB的中点,
∴
∴MN=MC+CD+DN=12cm,
∴MN的长为12cm.
26.解:(1)跳绳最多的一次为:165+10=175(个)
答:小明在这20次跳绳练习中,1分钟最多跳175个.
(2)(+10)﹣(﹣11)=10+11=21(个)
答:小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多21个.
(3)165×20﹣11×4﹣6×5﹣2×3+4×6+10×2=3264(个)
答:小明在这20次跳绳练习中,累计跳绳3264个.
27.解:(1)∵OC是∠AOD的平分线,
∴∠AOC=∠DOC.
∵OE是∠BOD的平分线,
∴∠BOE=∠DOE,
所以.
(2)设∠BOE=x,则∠DOE=x.
∵∠EOD﹣∠COD=30°,
∴∠COD=∠AOC=x﹣30°,
∴∠AOD=2∠AOC=2(x﹣30°).
∴∠BOC=3∠AOD,
∴可列方程为x+x+x﹣30°=3×2(x﹣30°),
解得x=50°,
即∠BOE的度数为50°.
一.选择题(共10小题,满分30分,每小题3分)
1.下列各数中,数值最大的是( )
A.5:9
B.55%
C.0.555
D.
2.某一时刻,时钟上显示的时间是9点30分,则此时时针与分针的夹角是( )
A.75°
B.90°
C.105°
D.120°
3.下列调查中,最适合采用全面调查(普查)的是( )
A.对我市中学生近视情况的调查
B.对我市市民国庆出游情况的调查
C.对全国人民掌握新冠防疫知识情况的调查
D.对我国自行研制的大型飞机C919各零部件质量情况的调查
4.实数a、b、c、d在数轴上的对应点的位置如图所示,在这四个数中,绝对值最小的数是( )
A.a
B.b
C.c
D.d
5.在立方体六个面上,分别标上“我、爱、华、侨、中、学”,如图是立体的三种不同摆法,则三种摆法的左侧面上三个字分别是( )
A.爱、华、侨
B.爱、中、学
C.中、我、侨
D.中、学、侨
6.在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )
A.﹣54
B.54
C.﹣558
D.558
7.下列说法正确的是( )
A.4π是一次单项式
B.
+x﹣3是二次三项式
C.﹣的系数是﹣2
D.﹣x的系数是﹣1
8.今年我市有近3500名考生参加中考,为了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析,这个问题中样本是( )
A.每位考生的数学成绩
B.3500名考生的数学成绩
C.被抽取的800名考生的数学成绩
D.被抽取的800名学生
9.将34.945取近似数精确到十分位,正确的是( )
A.34.9
B.35.0
C.35
D.35.05
10.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图形有10个正三角形,…依此规律,若第n个图案有2020个三角形,则n=( )
A.670
B.672
C.673
D.676
二.填空题(共10小题,满分30分,每小题3分)
11.2020年6月23日,北斗三号最后一颗全球组网卫星从西昌发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为
.
12.如果﹣a=2,则a=
.
13.某班班主任把本班学生体育期末考试成绩绘制成扇形统计图,已知全班有40名学生,其中体育成绩优秀的有16人,则代表体育成绩优秀的扇形所对应的圆心角度数是
.
14.在90%,+8,0,﹣15,﹣0.7,+,19中正数有
个.
15.已知两个单项式3xym与﹣3xny2的和为0,则m+n的值是
.
16.如图,将长方形纸片ABCD沿直线EN、EM进行折叠后(点E在AB边上),B′点刚好落在A′E上,若折叠角∠AEN=30°15′,则另一个折叠角∠BEM=
.
17.如图,点A、B为数轴上的两点,O为原点,A、B表示的数分别是x、x+2,B、O两点之间的距离等于A、B两点间的距离,则x的值是
.
18.某校为了了解初二年级600名学生每天完成作业所用时间的情况,从中对30名学生每完成作业所用时间进行了抽查,这个问题中的样本容量是
.
19.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b=
.
20.一个“数值转换机”按如图的程序计算,例如:输入的数为36,则经过一次运算即可输出结果106.若输出的结果127是经过两次运算才输出的,则输入的数是
.
三.解答题(共7小题,满分60分)
21.如图,已知直线l和直线外三点A,B,C,按下列要求画图:
(1)画射线AB;
(2)连接BC;
(3)反向延长BC至D,使得BD=BC;
(4)在直线l上确定点E,使得AE+CE最小.
22.计算:(﹣1)2﹣|2﹣5|÷(﹣3)×(1﹣).
23.先化简再求值:3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)],其中.
24.为了解某校七年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组
频数
1.2≤x<1.6
a
1.6≤x<2.0
12
2.0≤x<2.4
b
2.4≤x<2.8
10
请根据图表中所提供的信息,完成下列问题:
(1)求a,b的值,并将频数分布直方图补充完整;
(2)该校七年级共有800名学生,估计该年级学生立定跳远成绩在1.6≤x<2.0范围内的学生有多少人?
25.如图,C,D是线段AB上的两点,已知M,N分别为AC,DB的中点,AB=18cm,且AC:CD:DB=1:2:3,求线段MN的长.
26.小明练习跳绳.以1分钟跳165个为目标,并把20次1分钟跳绳的数量记录如表(超过165个的部分记为“+”,少于165个的部分记为“﹣”)
与目标数量的差异(单位:个)
﹣11
﹣6
﹣2
+4
+10
次数
4
5
3
6
2
(1)小明在这20次跳绳练习中,1分钟最多跳多少个?
(2)小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多几个?
(3)小明在这20次跳绳练习中,累计跳绳多少个?
27.如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
(1)若∠AOB=120°,则∠COE是多少度?
(2)如果∠BOC=3∠AOD,∠EOD﹣∠COD=30°,那么∠BOE是多少度?
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:5:9=0.,
55%=0.55,
=0.6,
∵0.,0.55,0.555,0.6中0.6最大,
∴数值最大的是.
故选:D.
2.解:时针与分针相距3+=(份),
时钟面上的时针与分针的夹角是30°×=105°,
故选:C.
3.解:A、对我市中学生近视情况的调查,人数众多,应采用抽样调查,故此选项不合题意;
B、对我市市民国庆出游情况的调查,人数众多,应采用抽样调查,故此选项不合题意;
C、对全国人民掌握新冠防疫知识情况的调查,人数众多,应采用抽样调查,故此选项不合题意;
D、对我国自行研制的大型飞机C919各零部件质量情况的调查,意义重大,应采用全面调查,故此选项符合题意;
故选:D.
4.解:由图可知:c到原点O的距离最短,
所以在这四个数中,绝对值最小的数是c;
故选:C.
5.解:根据三个图形的汉字,可推断出来,和我相对的就是华.和侨相对的就是爱.和中相对的就是学.
∴三种摆法的左侧面上三个字分别是爱、中、学.
故选:B.
6.解:把x=2代入计算程序中得:(2﹣8)×9=﹣54,
把x=﹣54代入计算程序中得:(﹣54﹣8)×9=﹣558,
则输出结果为﹣558,
故选:C.
7.解:A、4π是数字,是零次单项式,不符合题意;
B、+x﹣3不是整式,不符合题意;
C、﹣的系数为﹣,不符合题意;
D、﹣x的系数是﹣1,符合题意,
故选:D.
8.解:A是个体,B是总体,C是样本,今年我市有近3500名考生参加中考,为了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析,这个问题中样本是抽取的800名考生的数学成绩为样本.
故选:C.
9.解:34.945取近似数精确到十分位是34.9;
故选:A.
10.解:∵第(1)个图案有3+1=4个三角形,
第(2)个图案有3×2+1=7个三角形,
第(3)个图案有3×3+1=10个三角形,
…
∴第n个图案有(3n+1)个三角形.
根据题意可得:3n+1=2020,
解得:n=673,
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:将36000用科学记数法表示应为3.6×104,
故答案为:3.6×104.
12.解:∵﹣a=2,
∴a=﹣2.
故答案为:2.
13.解:根据题意得360°×=144°,
故答案为:144°.
14.解:在90%,+8,0,﹣15,﹣0.7,+,19中正数有:
90%,+8,+,19,共有4个,
故答案为:4.
15.解:∵两个单项式3xym与﹣3xny2的和为0,
∴两个单项式是同类项,
即m=2,n=1,
∴m+n=3.
故答案为:3.
16.解:由折叠性质得:∠AEN=∠A′EN,∠BEM=∠B′EM,
∴∠A′EN=30°15′,
∠BEM=(180°﹣∠AEN﹣∠A′EN)=(180°﹣30°15′﹣30°15′)=59°45′,
故答案为:59°45′.
17.解:根据题意得:0﹣(x+2)=x+2﹣x,
解得:x=﹣4.
故答案为:﹣4.
18.解:∵某校为了了解初二年级600名学生每天完成作业所用时间的情况,从中对30名学生每完成作业所用时间进行了抽查,
∴这个问题中的样本容量是30.
故答案为:30.
19.解:如图:2条直线相交有1个交点,
3条直线相交有1+2个交点,
4条直线相交有1+2+3个交点,
5条直线相交有1+2+3+4个交点,
6条直线相交有1+2+3+4+5个交点,
…
n直线相交有个交点.
∴,而b=1,
∴
故答案为:.
20.解:根据题意得:3x﹣2=127,
解得:x=43,
可得3x﹣2=43,
解得:x=15,
则输入的数是15,
故答案为:15
三.解答题(共7小题,满分60分)
21.解:(1)射线AB,如图所示;
(2)线段BC,如图所示,
(3)线段BD如图所示
(4)点E即为所求;
22.解:(﹣1)2﹣|2﹣5|÷(﹣3)×(1﹣)
=1﹣3÷(﹣3)×
=1+3×
=1+
=.
23.解:原式=3x2﹣6xy﹣[3x2﹣2y+2xy+2y]
=3x2﹣6xy﹣(3x2+2xy)
=3x2﹣6xy﹣3x2﹣2xy
=﹣8xy
当时
原式=﹣8×(﹣)×(﹣3)=﹣12.
24.解:(1)由频数分布直方图可知,a=8,
b=50﹣8﹣12﹣10=20,
补全的频数分布直方图如右图所示;
(2)800×=192(人),
答:该年级学生立定跳远成绩在1.6≤x<2.0范围内的学生有192人.
25.解:设AC,CD,DB的长分别为xcm,2xcm,3xcm
∵AC+CD+DB=AB,AB=18cm
∴x+2x+3x=18
解得x=3
∴AC=3cm,CD=6cm,DB=9cm
∵M,N为AC,DB的中点,
∴
∴MN=MC+CD+DN=12cm,
∴MN的长为12cm.
26.解:(1)跳绳最多的一次为:165+10=175(个)
答:小明在这20次跳绳练习中,1分钟最多跳175个.
(2)(+10)﹣(﹣11)=10+11=21(个)
答:小明在这20次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多21个.
(3)165×20﹣11×4﹣6×5﹣2×3+4×6+10×2=3264(个)
答:小明在这20次跳绳练习中,累计跳绳3264个.
27.解:(1)∵OC是∠AOD的平分线,
∴∠AOC=∠DOC.
∵OE是∠BOD的平分线,
∴∠BOE=∠DOE,
所以.
(2)设∠BOE=x,则∠DOE=x.
∵∠EOD﹣∠COD=30°,
∴∠COD=∠AOC=x﹣30°,
∴∠AOD=2∠AOC=2(x﹣30°).
∴∠BOC=3∠AOD,
∴可列方程为x+x+x﹣30°=3×2(x﹣30°),
解得x=50°,
即∠BOE的度数为50°.
同课章节目录
