二次函数图像及性质(教学案)
图片预览
文档简介
中考复习目标:二次函数图像及性质(教学案)
【课标解读】----------把握复习方向
会用配方法、公式法确定抛物线的开口方向、顶点坐标、对称轴、最大值或最小值
会画抛物线并由图像确定抛物线的增减性;
会用待定系数法确定二次函数的关系式
会把实际问题转化为二次函数的问题,并借助二次函数的性质讨论实际问题的最值问题
【考点链接】------点击知识要点
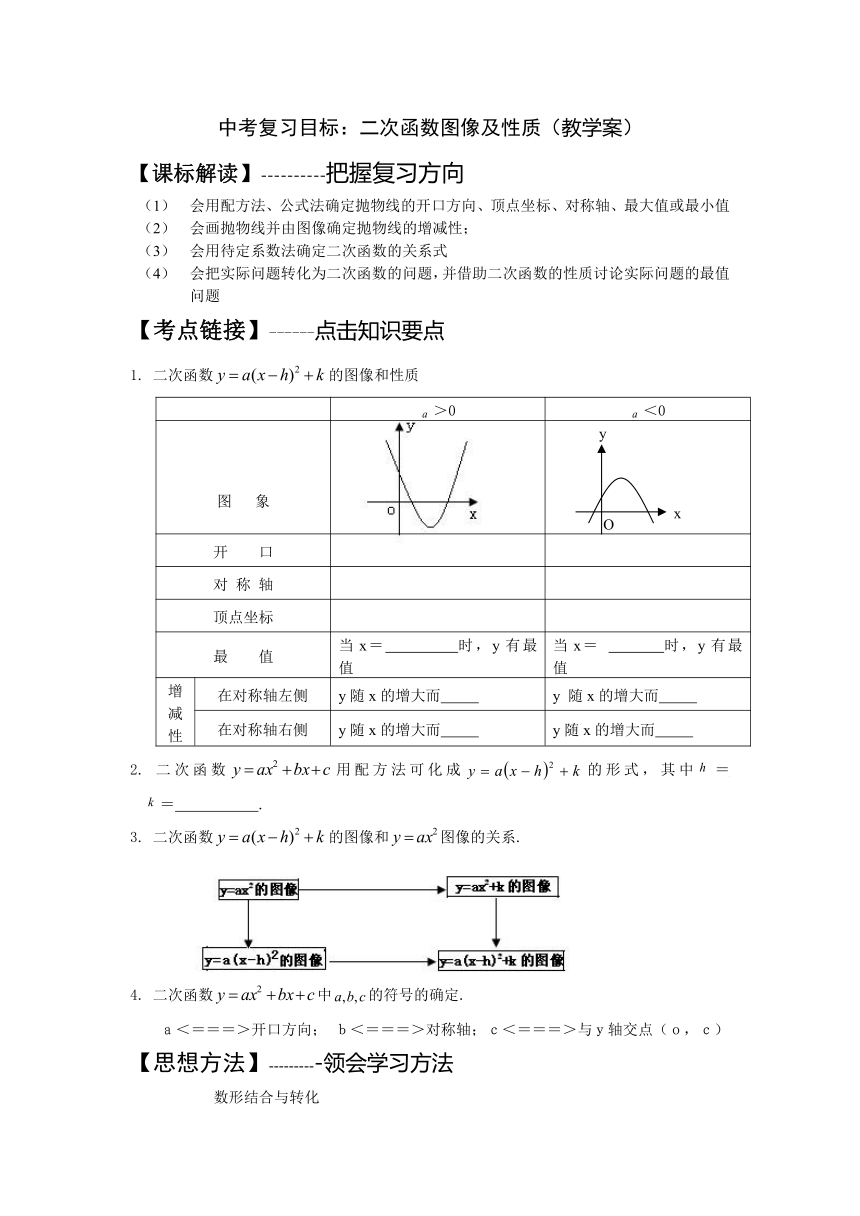
1. 二次函数的图像和性质
>0 <0
图 象
开 口
对 称 轴
顶点坐标
最 值 当x= 时,y有最 值 当x= 时,y有最 值
增减性 在对称轴左侧 y随x的增大而 y 随x的增大而
在对称轴右侧 y随x的增大而 y随x的增大而
2. 二次函数用配方法可化成的形式,其中= = .
3. 二次函数的图像和图像的关系.
4. 二次函数中的符号的确定.
a<===>开口方向; b<===>对称轴;c<===>与y轴交点(o,c)
【思想方法】----------领会学习方法
数形结合与转化
【典例精析】 --------尝试挑战应用
例1 已知二次函数,
(1) 用配方法把该函数化为
(其中a、h、k都是常数且a≠0)形式,并画
出这个函数的图像,根据图象指出函数的对称
轴和顶点坐标.
(2) 求函数的图象与x轴的交点坐标.
例2 已知抛物线与x轴有两个不同的交点.
(1)求c的取值范围;
(2)抛物线与x轴两交点的距离为2,求c的值.
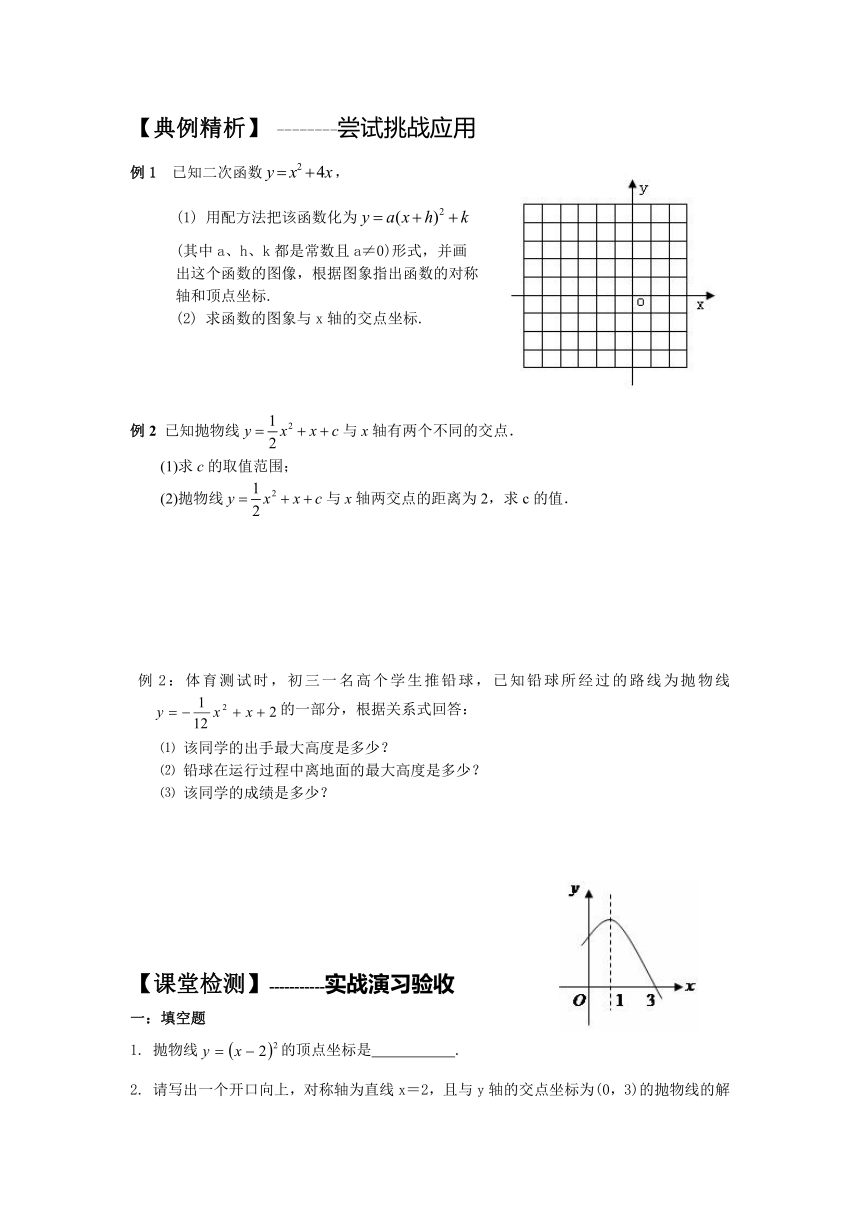
例2:体育测试时,初三一名高个学生推铅球,已知铅球所经过的路线为抛物线的一部分,根据关系式回答:
⑴ 该同学的出手最大高度是多少?
⑵ 铅球在运行过程中离地面的最大高度是多少?
⑶ 该同学的成绩是多少?
【课堂检测】-----------实战演习验收
一:填空题
1. 抛物线的顶点坐标是 .
2. 请写出一个开口向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式 .
3.已知二次函数的部分图象如右图所示,则关于的一元二次方程的解为 .
4. 函数与在同一坐标系中的大致图象是( )
5. 已知函数y=x2-2x-2的图象如图1所示,根据其中提供的信息,可求得使
y≥1成立的x的取值范围是( )
A.-1≤x≤3 B.-3≤x≤1 C.x≥-3 D.x≤-1或x≥3
6将抛物线y=x2-2x向上平移3个单位,再向右平移4个单位等到的抛物线是_______.
二选择题
7若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
X -7 -6 -5 -4 -3 -2
y -27 -13 -3 3 5 3
则当x=1时,y的值为( )
A.5 B.-3 C.-13 D.-27
8已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
A.a>0 B.当x>1时,y随x的增大而增大
C.c<0 D.3是方程ax2+bx+c=0的一个根
9某同学利用描点法画二次函数(的图象时,列出的部分数据如下表:
0 1 2 3 4
3 0 -2 0 3
经检查,发现表格中恰好有一组数据计算错误,请你根据上述信息写出该二次函数的解
析式为( ) A B C D
10如图,已知⊙P的半径为2,圆心P在抛物线上运动,当⊙P与轴相切时,圆心P的坐标为( )
A B C D
三解答题
11用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m,窗户的透光面积为y m2,y与x的函数图象如图2所示.
⑴ 观察图象,当x为何值时,窗户透光面积最大?
⑵ 当窗户透光面积最大时,窗框的另一边长是多少?
12已知二次函数y = - x2 - x + .
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y < 0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
y
x
O
【课标解读】----------把握复习方向
会用配方法、公式法确定抛物线的开口方向、顶点坐标、对称轴、最大值或最小值
会画抛物线并由图像确定抛物线的增减性;
会用待定系数法确定二次函数的关系式
会把实际问题转化为二次函数的问题,并借助二次函数的性质讨论实际问题的最值问题
【考点链接】------点击知识要点
1. 二次函数的图像和性质
>0 <0
图 象
开 口
对 称 轴
顶点坐标
最 值 当x= 时,y有最 值 当x= 时,y有最 值
增减性 在对称轴左侧 y随x的增大而 y 随x的增大而
在对称轴右侧 y随x的增大而 y随x的增大而
2. 二次函数用配方法可化成的形式,其中= = .
3. 二次函数的图像和图像的关系.
4. 二次函数中的符号的确定.
a<===>开口方向; b<===>对称轴;c<===>与y轴交点(o,c)
【思想方法】----------领会学习方法
数形结合与转化
【典例精析】 --------尝试挑战应用
例1 已知二次函数,
(1) 用配方法把该函数化为
(其中a、h、k都是常数且a≠0)形式,并画
出这个函数的图像,根据图象指出函数的对称
轴和顶点坐标.
(2) 求函数的图象与x轴的交点坐标.
例2 已知抛物线与x轴有两个不同的交点.
(1)求c的取值范围;
(2)抛物线与x轴两交点的距离为2,求c的值.
例2:体育测试时,初三一名高个学生推铅球,已知铅球所经过的路线为抛物线的一部分,根据关系式回答:
⑴ 该同学的出手最大高度是多少?
⑵ 铅球在运行过程中离地面的最大高度是多少?
⑶ 该同学的成绩是多少?
【课堂检测】-----------实战演习验收
一:填空题
1. 抛物线的顶点坐标是 .
2. 请写出一个开口向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式 .
3.已知二次函数的部分图象如右图所示,则关于的一元二次方程的解为 .
4. 函数与在同一坐标系中的大致图象是( )
5. 已知函数y=x2-2x-2的图象如图1所示,根据其中提供的信息,可求得使
y≥1成立的x的取值范围是( )
A.-1≤x≤3 B.-3≤x≤1 C.x≥-3 D.x≤-1或x≥3
6将抛物线y=x2-2x向上平移3个单位,再向右平移4个单位等到的抛物线是_______.
二选择题
7若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
X -7 -6 -5 -4 -3 -2
y -27 -13 -3 3 5 3
则当x=1时,y的值为( )
A.5 B.-3 C.-13 D.-27
8已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
A.a>0 B.当x>1时,y随x的增大而增大
C.c<0 D.3是方程ax2+bx+c=0的一个根
9某同学利用描点法画二次函数(的图象时,列出的部分数据如下表:
0 1 2 3 4
3 0 -2 0 3
经检查,发现表格中恰好有一组数据计算错误,请你根据上述信息写出该二次函数的解
析式为( ) A B C D
10如图,已知⊙P的半径为2,圆心P在抛物线上运动,当⊙P与轴相切时,圆心P的坐标为( )
A B C D
三解答题
11用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m,窗户的透光面积为y m2,y与x的函数图象如图2所示.
⑴ 观察图象,当x为何值时,窗户透光面积最大?
⑵ 当窗户透光面积最大时,窗框的另一边长是多少?
12已知二次函数y = - x2 - x + .
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y < 0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
y
x
O
同课章节目录
