吉林省白城市重点高中2020-2021学年高二下学期6月月考数学(文)试卷 Word版含答案
文档属性
| 名称 | 吉林省白城市重点高中2020-2021学年高二下学期6月月考数学(文)试卷 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 00:00:00 | ||
图片预览




文档简介
白城市重点高中2020-2021学年高二下学期6月月考
(文科数学)
考试说明:本试卷分第I卷(选择题)和第II卷(非选择题)两部分,
满分150分,考试时间120分钟.
(1)答题前,考生先将自己的姓名、准考证号码填写清楚;
(2)选择题必须使用2B铅笔填涂, 非选择题必须使用0.5毫米黑色字迹的签字笔书写, 字体工整,
字迹清楚;
(3)请在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效;
(4)保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一个是符合题目要求的.
1.已知集合,,则( )
2.已知复数,则的等于( )
3.若函数为上的奇函数,且当时,,则的值为( )
4.已知向量,,且,那么实数的值是( )
5.双曲线的渐近线方程为( )
6.《九章算术》第三章“衰分”介绍比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.如:已知三人分配奖金的衰分比为,若分得奖金元,则所分得奖金分别为元和元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得单位奖励元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金,则“衰分比”与丁所获得的奖金分别为( )
元 元 元 元
7.已知球面上三点,如果,且球的体积为,则球心到平面的距离为( )
8.为了得到函数的图象,只需把函数的图象上所有的点( )
向左平移个单位 向右平移个单位
向左平移个单位 向右平移个单位
9.已知椭圆:的左,右焦点分别为,为椭圆上一点,,,则椭圆的离心率为( )
10.一艘轮船按照北偏东方向,以18海里/时的速度沿直线航行,一座灯塔原来在轮船的南偏东方向上,经过分钟的航行,此时轮船与灯塔的距离为海里,则灯塔与轮船原来的距离为( )
海里 海里 海里 海里
11.如图,在底面为正方形,侧棱垂直于底面的四棱柱中,,则异面直线与所成角的余弦值为( )
12.已知函数,若,且,则的取值范围为( )
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.将答案填在机读卡上相应的位置.
13.若命题“”是真命题,则的取值范围是________;
14.已知满足则最大值为_________;
15.已知直线过定点,点在直线上,则的最小值是_________;
16.阿波罗尼斯(古希腊数学家,约公元前年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数且的点的轨迹是圆,后人将这个圆称为阿氏圆,现有,,,则的面积最大值为_____________;
三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)
在中,,,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)的值;
(2)角的大小和的面积.
条件①:;条件②:.
注:如果选择条件①?条件②分别解答,按第一个解答计分.
18.(本小题满分12分)
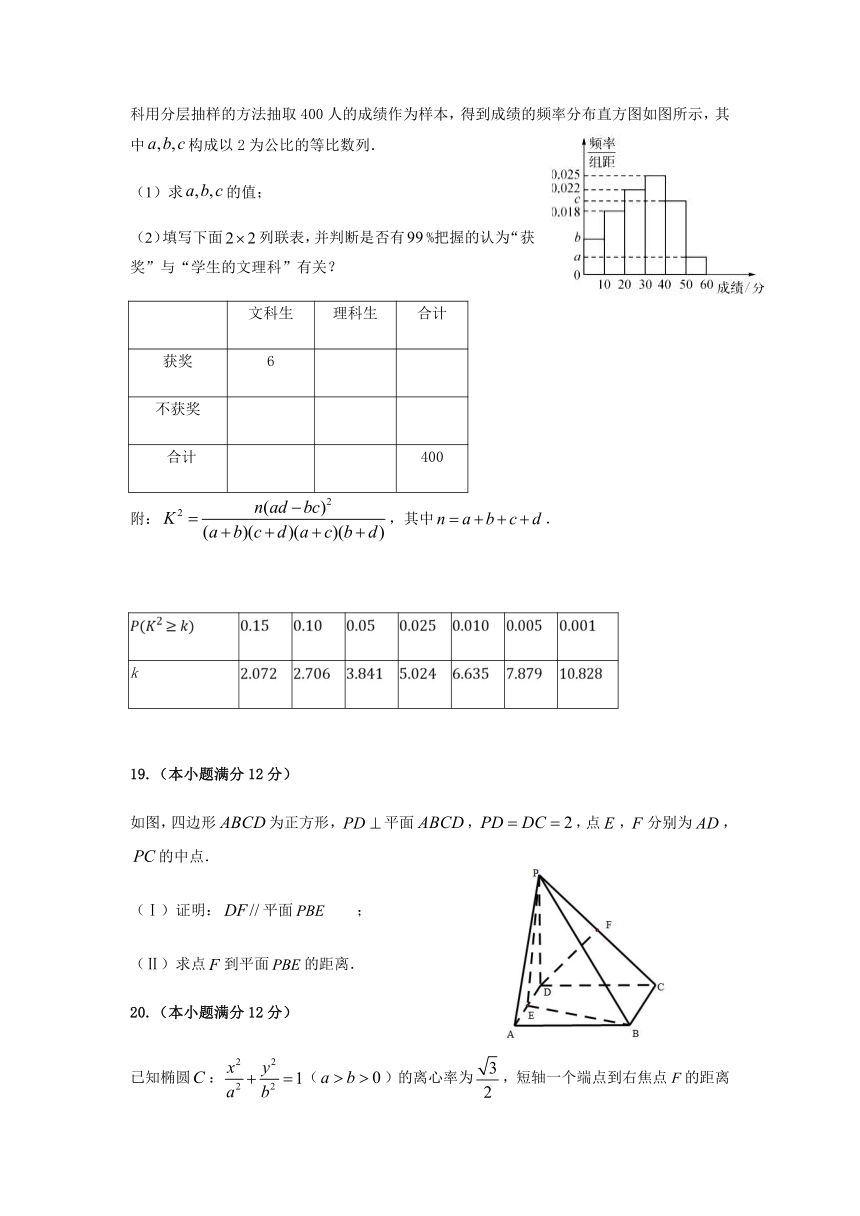
为调研高中生的作文水平,在某市普通高中的某次联考中,参考的文科生与理科生人数之比为1:4,且成绩分布在的范围内,规定分数在50以上含50)的作文获奖,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图如图所示,其中构成以2为公比的等比数列.
(1)求的值;
(2)填写下面列联表,并判断是否有%把握的认为“获奖”与“学生的文理科”有关?
文科生 理科生 合计
获奖 6
不获奖
合计
400
附:,其中.
k
19.(本小题满分12分)
如图,四边形为正方形,平面,,点,分别为,的中点.
(Ⅰ)证明:平面;
(Ⅱ)求点到平面的距离.
20.(本小题满分12分)
已知椭圆:()的离心率为,短轴一个端点到右焦点F的距离为.
(1)求椭圆的方程;
(2)若直线与椭圆相交于不同两点,且(为坐标原点),求的取值范围.
21.(本小题满分12分)
已知函数.
(1)当时,求在处的切线方程;
(2)当时,求证:对任意恒成立;
(3)设,请直接写出在上的零点个数.
22.(本小题满分10分)
在直角坐标系中,曲线的参数方程是(是参数),以原点为极点,轴的正半轴为极轴建立极坐标系.
(1)求曲线的极坐标方程;
(2)在曲线上取一点,直线绕原点逆时针旋转,交曲线于点,求的最大值.
白城市重点高中2020-2021学年高二下学期6月月考
(文科数学)答案
一、每小题5分
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D A B C B A D C C A D B
二、每小题5分
13.;14.; 15.; 16..
17.(本小题满分12分)
【解析】选择①:
(1)因为,,,
所以,即,
整理得,解得或(舍去),故............................................6
(2)因为,,
所以,......................................................12
选择②:
(1)因为,,,,
所以,
因为,所以,即,解得........................................6
(2)因为,,,,
所以
,
因为,,所以,
......................................................................12
18.(本小题满分12分)
解:由频率分布直方图可知,,
因为a,b,c构成以2为公比的等比数列,所以,解得,
所以,.故,,. ………………4分
获奖的人数为人,因为参考的文科生与理科生人数之比为1:4,
所以400人中文科生的数量为,理科生的数量为. ……………6分
由表可知,获奖的文科生有6人,所以获奖的理科生有人,不获奖的文科生有人.于是可以得到列联表如下:
文科生 理科生 合计
获奖 6 14 20
不获奖 74 306 380
合计 80 320 400
.....................................8分
……………………………10分
所以没有%把握的认为“获奖”与“学生的文理科”有关.............................12分
(本小题满分12分)
(1)证明:取点是的中点,连接,,则,且,
∵且,
∴且,
∴四边形为平行四边形,
∴,∴平面.........................................6
(Ⅱ)解:由(Ⅰ)知平面,所以点到平面的距离与到平面的距离是相等的,故转化为求点到平面的距离,设为.
利用等体积法:,即,,
∵,,∴,∴....................................12
(本小题满分12分)
(1) ..........4
(2)设,由直线与椭圆联立得:,,.....................................................8
又因为,所以得:
所以或........................................................................12
(本小题满分12分)
(1)当时,,
,
所以在处的切线方程为,即.............................4
(2)要证恒成立,即证,
即证,即证恒成立,
设,
令,当时,,
则,即对任意恒成立,
所以在单调递减,所以.
因为,所以恒成立,结论得证....................................................8
在上有2个零点...........................................................................12
(本小题满分10分)
(1)由消去得曲线的普通方程为.
所以的极坐标方程为,即......................5
(2)不妨设,,,,,
则
当时,取得最大值,最大值为.......................................10
(文科数学)
考试说明:本试卷分第I卷(选择题)和第II卷(非选择题)两部分,
满分150分,考试时间120分钟.
(1)答题前,考生先将自己的姓名、准考证号码填写清楚;
(2)选择题必须使用2B铅笔填涂, 非选择题必须使用0.5毫米黑色字迹的签字笔书写, 字体工整,
字迹清楚;
(3)请在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效;
(4)保持卡面清洁,不得折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一个是符合题目要求的.
1.已知集合,,则( )
2.已知复数,则的等于( )
3.若函数为上的奇函数,且当时,,则的值为( )
4.已知向量,,且,那么实数的值是( )
5.双曲线的渐近线方程为( )
6.《九章算术》第三章“衰分”介绍比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.如:已知三人分配奖金的衰分比为,若分得奖金元,则所分得奖金分别为元和元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得单位奖励元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金,则“衰分比”与丁所获得的奖金分别为( )
元 元 元 元
7.已知球面上三点,如果,且球的体积为,则球心到平面的距离为( )
8.为了得到函数的图象,只需把函数的图象上所有的点( )
向左平移个单位 向右平移个单位
向左平移个单位 向右平移个单位
9.已知椭圆:的左,右焦点分别为,为椭圆上一点,,,则椭圆的离心率为( )
10.一艘轮船按照北偏东方向,以18海里/时的速度沿直线航行,一座灯塔原来在轮船的南偏东方向上,经过分钟的航行,此时轮船与灯塔的距离为海里,则灯塔与轮船原来的距离为( )
海里 海里 海里 海里
11.如图,在底面为正方形,侧棱垂直于底面的四棱柱中,,则异面直线与所成角的余弦值为( )
12.已知函数,若,且,则的取值范围为( )
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.将答案填在机读卡上相应的位置.
13.若命题“”是真命题,则的取值范围是________;
14.已知满足则最大值为_________;
15.已知直线过定点,点在直线上,则的最小值是_________;
16.阿波罗尼斯(古希腊数学家,约公元前年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数且的点的轨迹是圆,后人将这个圆称为阿氏圆,现有,,,则的面积最大值为_____________;
三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)
在中,,,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)的值;
(2)角的大小和的面积.
条件①:;条件②:.
注:如果选择条件①?条件②分别解答,按第一个解答计分.
18.(本小题满分12分)
为调研高中生的作文水平,在某市普通高中的某次联考中,参考的文科生与理科生人数之比为1:4,且成绩分布在的范围内,规定分数在50以上含50)的作文获奖,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图如图所示,其中构成以2为公比的等比数列.
(1)求的值;
(2)填写下面列联表,并判断是否有%把握的认为“获奖”与“学生的文理科”有关?
文科生 理科生 合计
获奖 6
不获奖
合计
400
附:,其中.
k
19.(本小题满分12分)
如图,四边形为正方形,平面,,点,分别为,的中点.
(Ⅰ)证明:平面;
(Ⅱ)求点到平面的距离.
20.(本小题满分12分)
已知椭圆:()的离心率为,短轴一个端点到右焦点F的距离为.
(1)求椭圆的方程;
(2)若直线与椭圆相交于不同两点,且(为坐标原点),求的取值范围.
21.(本小题满分12分)
已知函数.
(1)当时,求在处的切线方程;
(2)当时,求证:对任意恒成立;
(3)设,请直接写出在上的零点个数.
22.(本小题满分10分)
在直角坐标系中,曲线的参数方程是(是参数),以原点为极点,轴的正半轴为极轴建立极坐标系.
(1)求曲线的极坐标方程;
(2)在曲线上取一点,直线绕原点逆时针旋转,交曲线于点,求的最大值.
白城市重点高中2020-2021学年高二下学期6月月考
(文科数学)答案
一、每小题5分
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D A B C B A D C C A D B
二、每小题5分
13.;14.; 15.; 16..
17.(本小题满分12分)
【解析】选择①:
(1)因为,,,
所以,即,
整理得,解得或(舍去),故............................................6
(2)因为,,
所以,......................................................12
选择②:
(1)因为,,,,
所以,
因为,所以,即,解得........................................6
(2)因为,,,,
所以
,
因为,,所以,
......................................................................12
18.(本小题满分12分)
解:由频率分布直方图可知,,
因为a,b,c构成以2为公比的等比数列,所以,解得,
所以,.故,,. ………………4分
获奖的人数为人,因为参考的文科生与理科生人数之比为1:4,
所以400人中文科生的数量为,理科生的数量为. ……………6分
由表可知,获奖的文科生有6人,所以获奖的理科生有人,不获奖的文科生有人.于是可以得到列联表如下:
文科生 理科生 合计
获奖 6 14 20
不获奖 74 306 380
合计 80 320 400
.....................................8分
……………………………10分
所以没有%把握的认为“获奖”与“学生的文理科”有关.............................12分
(本小题满分12分)
(1)证明:取点是的中点,连接,,则,且,
∵且,
∴且,
∴四边形为平行四边形,
∴,∴平面.........................................6
(Ⅱ)解:由(Ⅰ)知平面,所以点到平面的距离与到平面的距离是相等的,故转化为求点到平面的距离,设为.
利用等体积法:,即,,
∵,,∴,∴....................................12
(本小题满分12分)
(1) ..........4
(2)设,由直线与椭圆联立得:,,.....................................................8
又因为,所以得:
所以或........................................................................12
(本小题满分12分)
(1)当时,,
,
所以在处的切线方程为,即.............................4
(2)要证恒成立,即证,
即证,即证恒成立,
设,
令,当时,,
则,即对任意恒成立,
所以在单调递减,所以.
因为,所以恒成立,结论得证....................................................8
在上有2个零点...........................................................................12
(本小题满分10分)
(1)由消去得曲线的普通方程为.
所以的极坐标方程为,即......................5
(2)不妨设,,,,,
则
当时,取得最大值,最大值为.......................................10
同课章节目录
