勾股定理

(共30张PPT)
课前导入 实验讲解
问题探讨 小结归纳
A
B
C
这是1955年希腊发行的一枚纪念邮票，邮票上的图案是根据一个著名的数学定理设计的。
这是1955年希腊发行的一枚纪念邮票，邮票上的图案是根据一个著名的数学定理设计的。
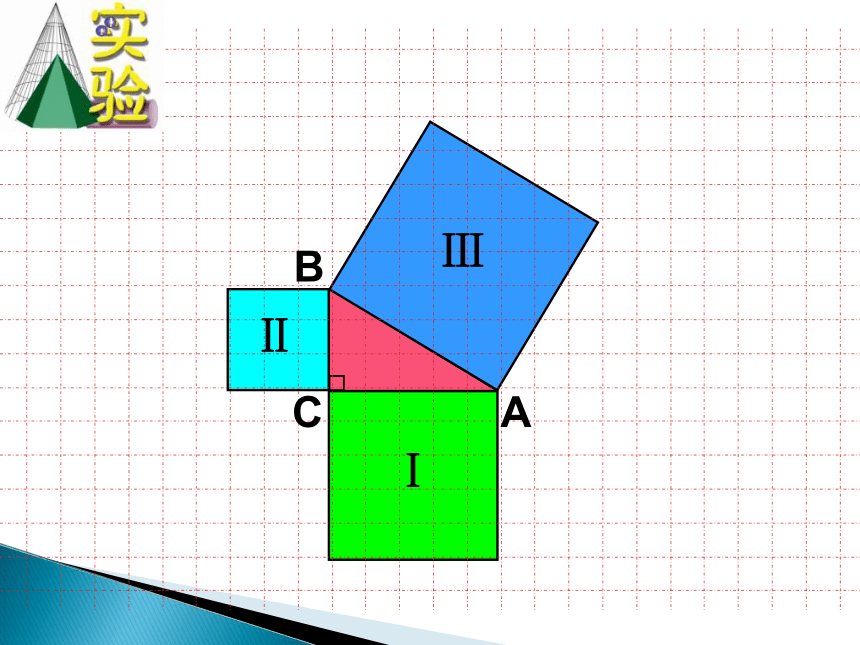
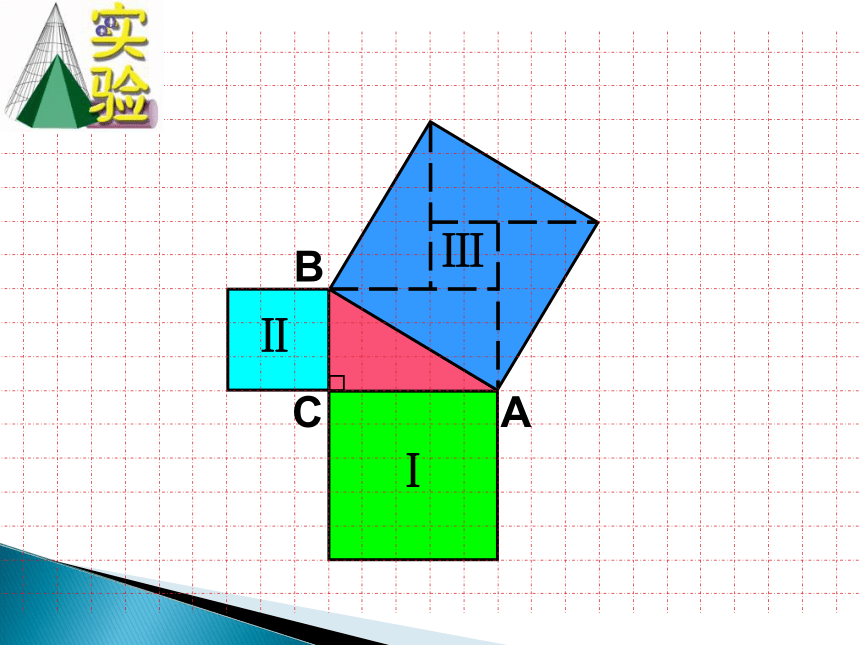
A
B
C
Ⅰ
Ⅱ
Ⅲ
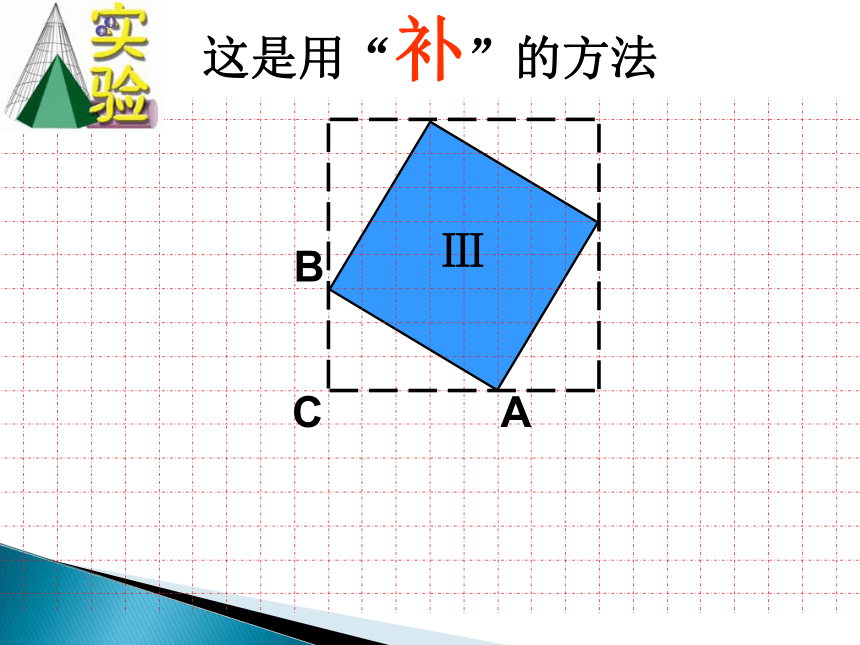
A
B
C
这是用“补”的方法
Ⅲ
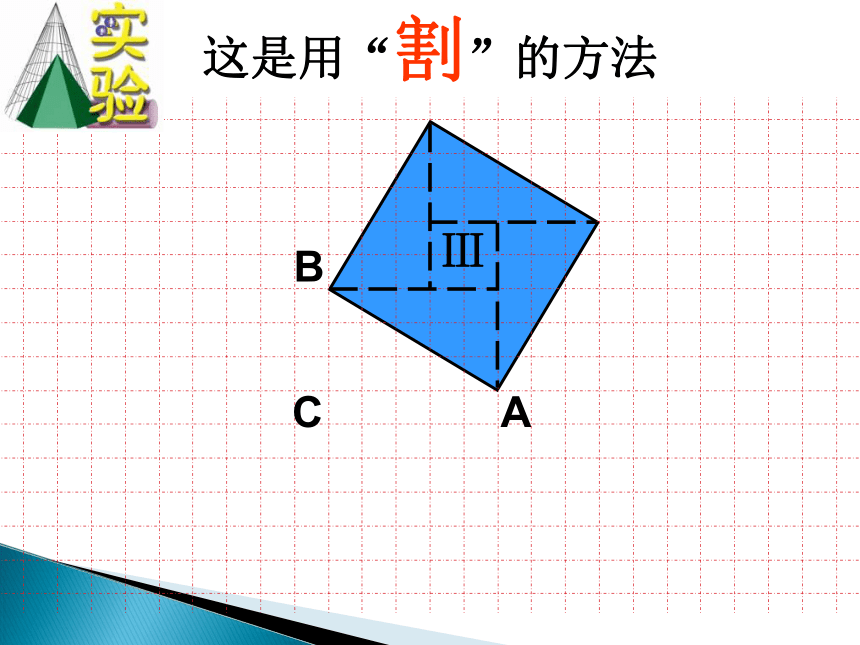
A
B
C
Ⅲ
这是用“割”的方法
A
B
C
Ⅰ
Ⅱ
Ⅲ
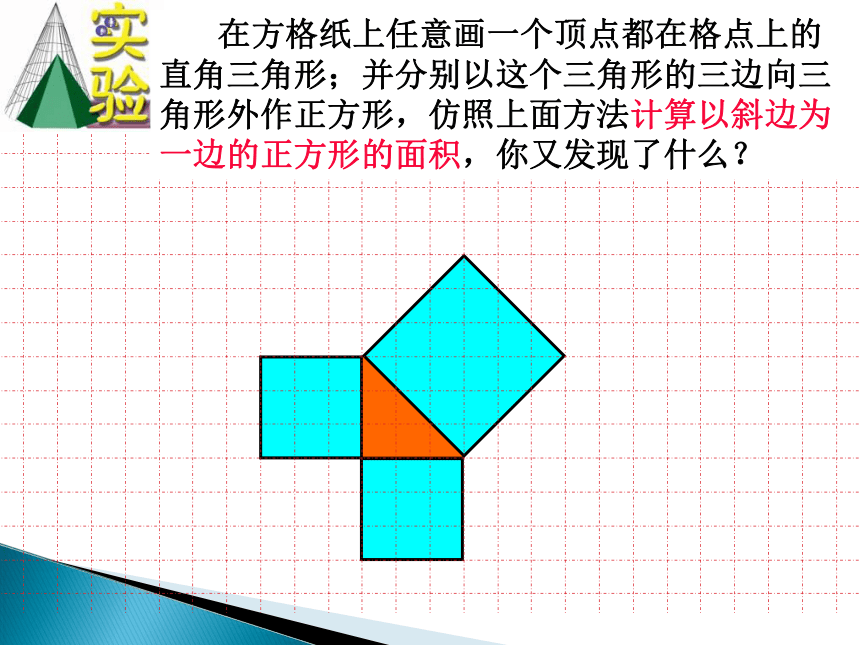
在方格纸上任意画一个顶点都在格点上的直角三角形；并分别以这个三角形的三边向三角形外作正方形，仿照上面方法计算以斜边为一边的正方形的面积，你又发现了什么？
在方格纸上任意画一个顶点都在格点上的直角三角形；并分别以这个三角形的三边向三角形外作正方形，仿照上面方法计算以斜边为一边的正方形的面积，你又发现了什么？
在方格纸上任意画一个顶点都在格点上的直角三角形；并分别以这个三角形的三边向三角形外作正方形，仿照上面方法计算以斜边为一边的正方形的面积，你又发现了什么？
在方格纸上任意画一个顶点都在格点上的直角三角形；并分别以这个三角形的三边向三角形外作正方形，仿照上面方法计算以斜边为一边的正方形的面积，你又发现了什么？
A
B
C
Ⅰ
Ⅱ
Ⅲ
直角三角形两直角边的平方和等于斜边的平方。
直角三角形两直角边的平方和等于斜边的平方。
a2 + b2 = c2
勾股定理
∵ △ABC为直角三角形
∴ AC2+BC2=AB2.
(或a2+b2=c2)
A
B
C
a
b
c
如果直角三角形两直角边分别为a、b,斜边为c，那么
勾股世界
我国是最早了解勾股定理的国家之一。三千多年前，周朝数学家商高就提出了“勾三股四弦五”的说法。
勾2 + 股2 = 弦2
股
勾
勾
较短的直角边称为 ，
股
较长的直角边称为 ，
直角三角形中
弦
斜边称为 。
弦
毕达哥拉斯
二千多年前，希腊的毕达哥拉斯学派证明了这个勾股定理，所以勾股定理又被称为“毕达哥拉斯定理”，不过毕达哥拉斯的发现比中国晚了500多年。
求下列图中正方形A、B、C的面积。
⑴
81
144
169
144
⑵
625
576
⑶
问题一
A
C
B
如图, 正方形Ⅰ的边长为7
B
A
C
D
Ⅰ
Ⅱ
Ⅲ
“勾股树”
你能求出正方形A、B、C、D的面积之和吗？
问题二
“勾股树”
问题三
求下列直角三角形中未知边的长。
12
5
x
⑴
x
8
17
⑵
x
20
16
⑶
问题三
D
x
3
A
B
C
4
13
求下列直角△BCD中未知边的长。
⑷
×
1.若直角三角形的两边长为3和4，则第三边为5.
（ ）
2.若a、b、c为Rt△ABC的三边,则a2+b2=c2.
（ ）
×
问题四
问题五
台风袭击中，一棵大树在离地面9米处断裂，树的顶部落在离树根底部12米处。这棵树原来有多高？
9米
12米
问题五
台风袭击中，一棵大树在离地面9米处断裂，树的顶部落在离树根底部12米处。这棵树原来有多高？
B
A
c
1. 课本47页，第１、２、3题；
2.查阅有关勾股定理的历史资料,
关注验证勾股定理的方法.