(人教版)高中数学选修2-2课件:第1章 导数及其应用1.1.1、2(38张)
文档属性
| 名称 | (人教版)高中数学选修2-2课件:第1章 导数及其应用1.1.1、2(38张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 15:15:54 | ||
图片预览







文档简介
第 一 章
导数及其应用
1.1 变化率与导数
1.1.1 变化率问题
1.1.2 导数的概念
自主学习 新知突破
1.了解实际问题中平均变化率的意义.
2.理解函数的平均变化率与瞬时变化率的概念.
3.理解并掌握导数的概念.
4.掌握求函数在一点处的导数的方法.
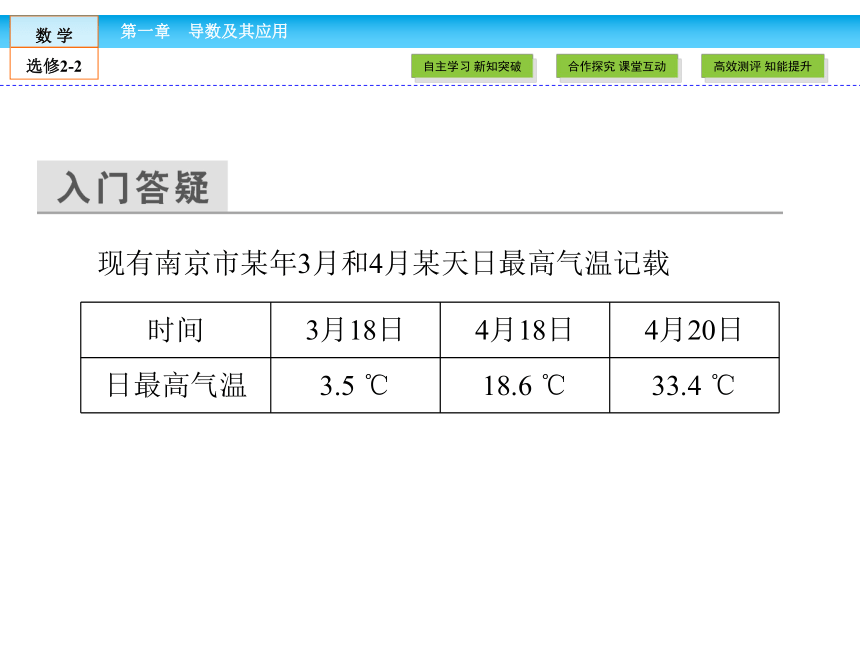
现有南京市某年3月和4月某天日最高气温记载
时间
3月18日
4月18日
4月20日
日最高气温
3.5 ℃
18.6 ℃
33.4 ℃
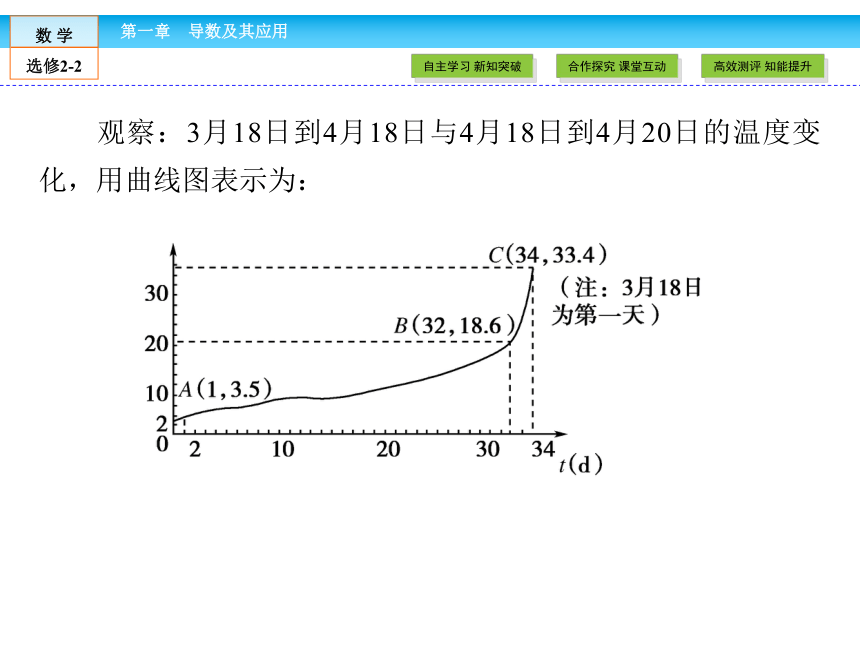
观察:3月18日到4月18日与4月18日到4月20日的温度变化,用曲线图表示为:
[问题1] “气温陡增”是一句生活用语,它的数学意义是什么?(形与数两方面)
[提示1] 曲线上BC之间一段几乎成了“直线”,由此联想如何量化直线的倾斜程度.
[问题2] 由点B上升到点C,必须考察yC-yB的大小,但仅仅注意yC-yB的大小能否精确量化BC段陡峭程度,为什么?
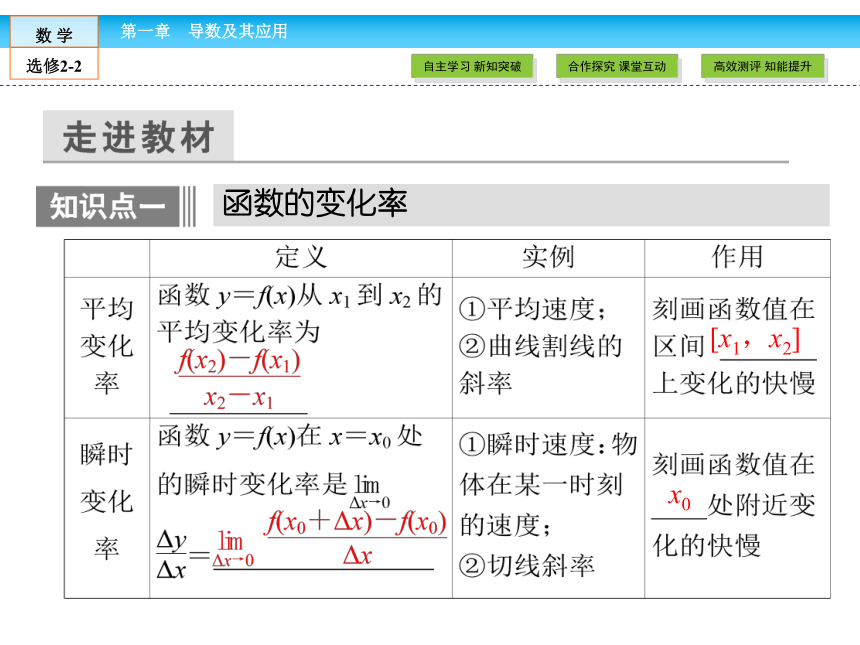
函数的变化率
[x1,x2]
x0
1.关于函数的平均变化率,应注意以下几点
(1)函数f(x)在x1处有定义.
(2)Δx是变量x2在x1处的改变量,且x2是x1附近的任意一点,即Δx=x2-x1≠0,但Δx可以为正,也可以为负.
(3)注意自变量与函数值的对应关系,公式中若Δx=x2-x1,则Δy=f(x2)-f(x1);若Δx=x1-x2,则Δy=f(x1)-f(x2).
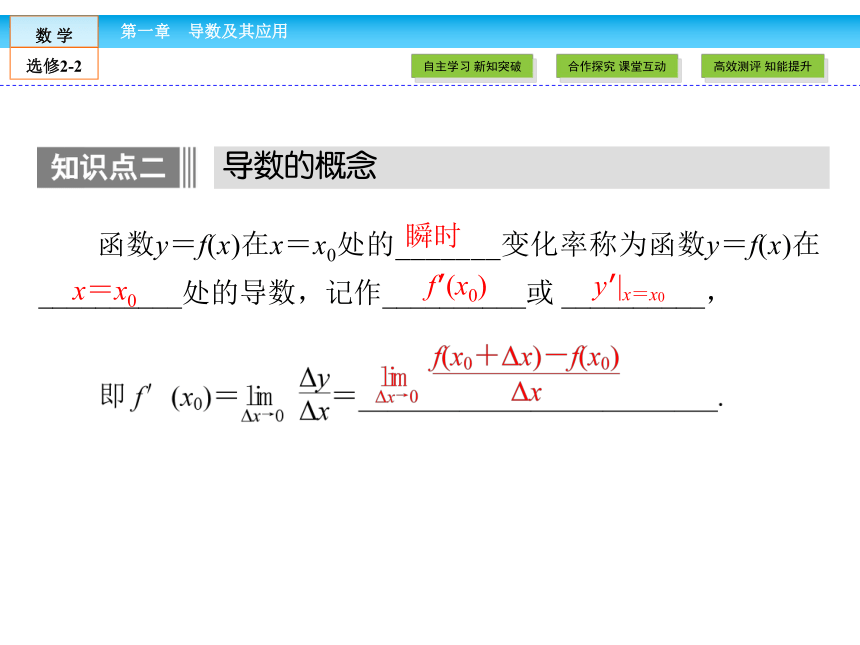
函数y=f(x)在x=x0处的_______变化率称为函数y=f(x)在__________处的导数,记作__________或 __________,
导数的概念
瞬时
x=x0
f′(x0)
y′|x=x0
2.对函数在某点处导数的认识
(1)函数在某点处的导数是一个定值,是函数在该点的函数值改变量与自变量的改变量比值的极限,不是变量.
(2)函数在x0处的导数f′(x0)只与x0有关,与Δx无关.
(3)导数可以描述任何事物的瞬时变化率,应用非常广泛.
1.已知函数y=f(x)=x2+1,则在x=2,Δx=0.1时,Δy的值为( )
A.0.40 B.0.41
C.0.43 D.0.44
解析: Δy=f(2.1)-f(2)=0.41.
答案: B
2.如果质点M按照规律s=3t2运动,则在t=3时的瞬时速度为( )
A.6 B.18
C.54 D.81
答案: B
3.一个物体的运动方程为s=1-t+t2.其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度为________.
答案: 5米/秒
合作探究 课堂互动
求函数的平均变化率
求函数y=f(x)=3x2+2在区间[x0,x0+Δx]上的平均变化率,并求当x0=2,Δx=0.1时平均变化率的值.
[思路点拨] 先求自变量的增量和函数值的增量,然后代入公式计算.
求物体的瞬时速度
已知函数f(x)=2x2+1.
(1)求函数f(x)在区间[x0,x0+Δx]上的平均变化率;
(2)求函数f(x)在区间[2,2.01]上的平均变化率;
(3)求函数f(x)在x=2处的瞬时变化率.
1.求瞬时变化率时要首先明确求哪个点处的瞬时变化率,然后,以此点为一端点取一区间计算平均变化率,并逐步缩小区间长度,根据平均变化率的变化情况估计出瞬时变化率.
求函数f(x)在某点处的导数
已知f(x)=x2+3.
(1)求f(x)在x=1处的导数;
(2)求f(x)在x=a处的导数.
3.已知函数y=2x2+4x.
(1)求函数在x=3处的导数;
(2)若函数在x0处的导数是12,求x0的值.
谢谢观看!
导数及其应用
1.1 变化率与导数
1.1.1 变化率问题
1.1.2 导数的概念
自主学习 新知突破
1.了解实际问题中平均变化率的意义.
2.理解函数的平均变化率与瞬时变化率的概念.
3.理解并掌握导数的概念.
4.掌握求函数在一点处的导数的方法.
现有南京市某年3月和4月某天日最高气温记载
时间
3月18日
4月18日
4月20日
日最高气温
3.5 ℃
18.6 ℃
33.4 ℃
观察:3月18日到4月18日与4月18日到4月20日的温度变化,用曲线图表示为:
[问题1] “气温陡增”是一句生活用语,它的数学意义是什么?(形与数两方面)
[提示1] 曲线上BC之间一段几乎成了“直线”,由此联想如何量化直线的倾斜程度.
[问题2] 由点B上升到点C,必须考察yC-yB的大小,但仅仅注意yC-yB的大小能否精确量化BC段陡峭程度,为什么?
函数的变化率
[x1,x2]
x0
1.关于函数的平均变化率,应注意以下几点
(1)函数f(x)在x1处有定义.
(2)Δx是变量x2在x1处的改变量,且x2是x1附近的任意一点,即Δx=x2-x1≠0,但Δx可以为正,也可以为负.
(3)注意自变量与函数值的对应关系,公式中若Δx=x2-x1,则Δy=f(x2)-f(x1);若Δx=x1-x2,则Δy=f(x1)-f(x2).
函数y=f(x)在x=x0处的_______变化率称为函数y=f(x)在__________处的导数,记作__________或 __________,
导数的概念
瞬时
x=x0
f′(x0)
y′|x=x0
2.对函数在某点处导数的认识
(1)函数在某点处的导数是一个定值,是函数在该点的函数值改变量与自变量的改变量比值的极限,不是变量.
(2)函数在x0处的导数f′(x0)只与x0有关,与Δx无关.
(3)导数可以描述任何事物的瞬时变化率,应用非常广泛.
1.已知函数y=f(x)=x2+1,则在x=2,Δx=0.1时,Δy的值为( )
A.0.40 B.0.41
C.0.43 D.0.44
解析: Δy=f(2.1)-f(2)=0.41.
答案: B
2.如果质点M按照规律s=3t2运动,则在t=3时的瞬时速度为( )
A.6 B.18
C.54 D.81
答案: B
3.一个物体的运动方程为s=1-t+t2.其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度为________.
答案: 5米/秒
合作探究 课堂互动
求函数的平均变化率
求函数y=f(x)=3x2+2在区间[x0,x0+Δx]上的平均变化率,并求当x0=2,Δx=0.1时平均变化率的值.
[思路点拨] 先求自变量的增量和函数值的增量,然后代入公式计算.
求物体的瞬时速度
已知函数f(x)=2x2+1.
(1)求函数f(x)在区间[x0,x0+Δx]上的平均变化率;
(2)求函数f(x)在区间[2,2.01]上的平均变化率;
(3)求函数f(x)在x=2处的瞬时变化率.
1.求瞬时变化率时要首先明确求哪个点处的瞬时变化率,然后,以此点为一端点取一区间计算平均变化率,并逐步缩小区间长度,根据平均变化率的变化情况估计出瞬时变化率.
求函数f(x)在某点处的导数
已知f(x)=x2+3.
(1)求f(x)在x=1处的导数;
(2)求f(x)在x=a处的导数.
3.已知函数y=2x2+4x.
(1)求函数在x=3处的导数;
(2)若函数在x0处的导数是12,求x0的值.
谢谢观看!
