(人教版)高中数学选修2-2课件:第1章 导数及其应用1.1.3(41张)
文档属性
| 名称 | (人教版)高中数学选修2-2课件:第1章 导数及其应用1.1.3(41张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 15:17:18 | ||
图片预览








文档简介
1.1.3 导数的几何意义
自主学习 新知突破
1.了解导函数的概念,理解导数的几何意义.
2.弄清函数在x=x0处的导数f′(x0)与导函数f′(x)的区别与联系.会求导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
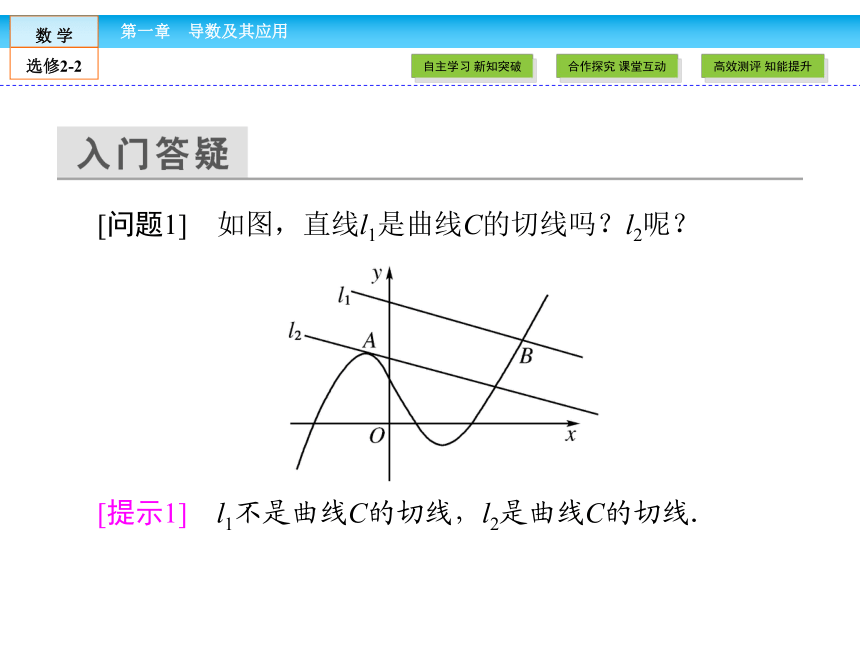
[问题1] 如图,直线l1是曲线C的切线吗?l2呢?
[提示1] l1不是曲线C的切线,l2是曲线C的切线.
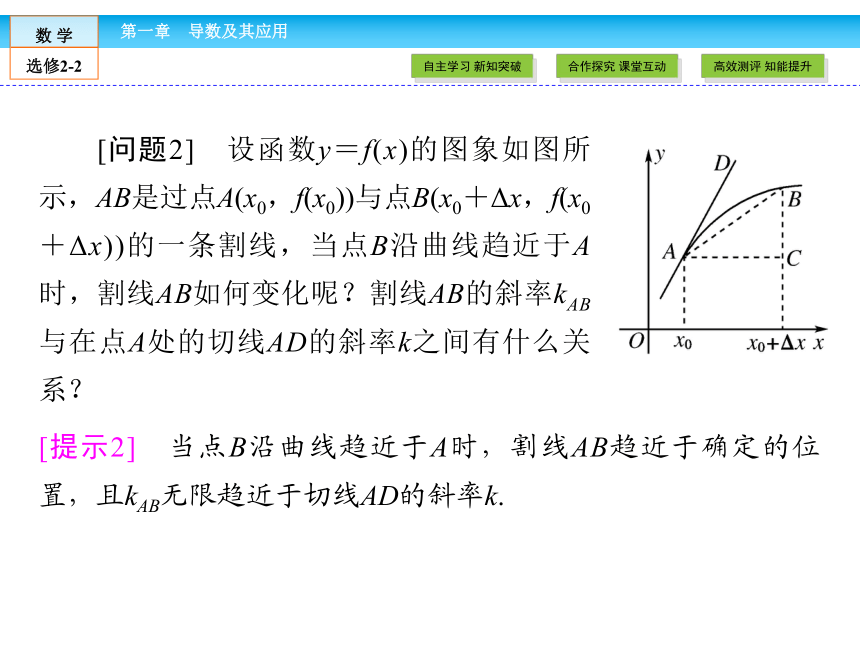
[问题2] 设函数y=f(x)的图象如图所示,AB是过点A(x0,f(x0))与点B(x0+Δx,f(x0+Δx))的一条割线,当点B沿曲线趋近于A时,割线AB如何变化呢?割线AB的斜率kAB与在点A处的切线AD的斜率k之间有什么关系?
[提示2] 当点B沿曲线趋近于A时,割线AB趋近于确定的位置,且kAB无限趋近于切线AD的斜率k.
导数的几何意义
切线
斜率k
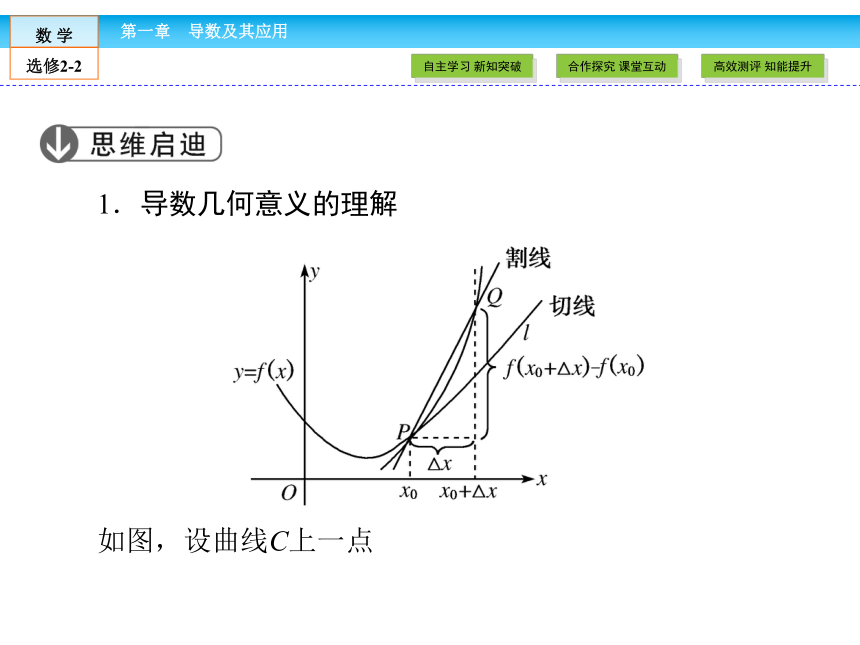
1.导数几何意义的理解
如图,设曲线C上一点
导函数
2.函数在某点处的导数与导函数的区别
(1)函数在某点处的导数是一个定值,导函数是一个函数;
(2)函数f(x)在x0处的导数就是导函数f′(x)在x=x0处的函数值.
1.设f′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在 B.与x轴平行或重合
C.与x轴垂直 D.与x轴相交
解析: 在点(x0,f(x0))处切线斜率为0的直线与x轴平行或重合,故选B.
答案: B
2.设曲线y=x2+x-2在点M处的切线斜率为3,则点M的坐标为( )
A.(0,-2) B.(1,0)
C.(0,0) D.(1,1)
答案: B
3.如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
解析: 点(5,f(5))在切线y=-x+8上,
∴f(5)=-5+8=3.
且f′(5)=-1,
∴f(5)+f′(5)=2.
答案: 2
合作探究 课堂互动
求曲线的切线方程
[思路点拨]
求曲线上某点(x0,y0)处切线方程的步骤:
特别提醒:在求切线方程的题目中,注意题干给出的点不一定在曲线上,即使在曲线上也不一定作为切点应用.
1.求曲线y=f(x)=x3+2x-1在点P(1,2)处的切线方程.
当Δx无限趋近于0时,3x2+2+3x·Δx+(Δx)2无限趋近于3x2+2.即f′(x)=3x2+2,所以f′(1)=5.
故点P处的切线斜率为k=5.
所以点P处的切线方程为y-2=5(x-1).
即5x-y-3=0.
求切点坐标
已知曲线y=x2+6的切线分别符合下列条件,求切点.
(1)平行于直线y=4x-3;
(2)垂直于直线2x-y+5=0.
设切点坐标为(x0,y0).
求切点坐标可以按以下步骤进行:
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
2.在曲线y=x2上过哪一点的切线.
(1)垂直于直线2x-6y+5=0;
(2)与x轴成135°的倾斜角.
导数几何意义的实际应用
“菊花”烟火是最壮观的烟花之一,制造时通常期望它在达到最高时爆裂.如果烟花距地面的高度h(m)与时间t(s)之间的关系式为h(t)=-4.9t2+14.7t+18,求烟花在t=2 s时的瞬时速度,并解释烟花升空后的运动状况.
[思路点拨] 烟花在t=2 s时的瞬时速度就是h′(2),即曲线h(t)在点t=2处的切线的斜率;而烟花升空后的运动状况,可以应用切线斜率的变化予以解释.
导数的几何意义是曲线的切线的斜率.反之,在曲线上取确定的点,作曲线的切线,则可以根据切线斜率的符号及绝对值的大小来确定曲线的升降情况及升降的快慢程度.
◎试求过点P(3,5)且与y=x2相切的直线方程.
【错因】 求曲线上的点P处的切线与求过点P的切线有区别,在点P处的切线,点P必为切点;求过点P的切线,点P未必是切点,应注意概念不同,其求法也有所不同.
谢谢观看!
自主学习 新知突破
1.了解导函数的概念,理解导数的几何意义.
2.弄清函数在x=x0处的导数f′(x0)与导函数f′(x)的区别与联系.会求导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
[问题1] 如图,直线l1是曲线C的切线吗?l2呢?
[提示1] l1不是曲线C的切线,l2是曲线C的切线.
[问题2] 设函数y=f(x)的图象如图所示,AB是过点A(x0,f(x0))与点B(x0+Δx,f(x0+Δx))的一条割线,当点B沿曲线趋近于A时,割线AB如何变化呢?割线AB的斜率kAB与在点A处的切线AD的斜率k之间有什么关系?
[提示2] 当点B沿曲线趋近于A时,割线AB趋近于确定的位置,且kAB无限趋近于切线AD的斜率k.
导数的几何意义
切线
斜率k
1.导数几何意义的理解
如图,设曲线C上一点
导函数
2.函数在某点处的导数与导函数的区别
(1)函数在某点处的导数是一个定值,导函数是一个函数;
(2)函数f(x)在x0处的导数就是导函数f′(x)在x=x0处的函数值.
1.设f′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在 B.与x轴平行或重合
C.与x轴垂直 D.与x轴相交
解析: 在点(x0,f(x0))处切线斜率为0的直线与x轴平行或重合,故选B.
答案: B
2.设曲线y=x2+x-2在点M处的切线斜率为3,则点M的坐标为( )
A.(0,-2) B.(1,0)
C.(0,0) D.(1,1)
答案: B
3.如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
解析: 点(5,f(5))在切线y=-x+8上,
∴f(5)=-5+8=3.
且f′(5)=-1,
∴f(5)+f′(5)=2.
答案: 2
合作探究 课堂互动
求曲线的切线方程
[思路点拨]
求曲线上某点(x0,y0)处切线方程的步骤:
特别提醒:在求切线方程的题目中,注意题干给出的点不一定在曲线上,即使在曲线上也不一定作为切点应用.
1.求曲线y=f(x)=x3+2x-1在点P(1,2)处的切线方程.
当Δx无限趋近于0时,3x2+2+3x·Δx+(Δx)2无限趋近于3x2+2.即f′(x)=3x2+2,所以f′(1)=5.
故点P处的切线斜率为k=5.
所以点P处的切线方程为y-2=5(x-1).
即5x-y-3=0.
求切点坐标
已知曲线y=x2+6的切线分别符合下列条件,求切点.
(1)平行于直线y=4x-3;
(2)垂直于直线2x-y+5=0.
设切点坐标为(x0,y0).
求切点坐标可以按以下步骤进行:
(1)设出切点坐标;
(2)利用导数或斜率公式求出斜率;
(3)利用斜率关系列方程,求出切点的横坐标;
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
2.在曲线y=x2上过哪一点的切线.
(1)垂直于直线2x-6y+5=0;
(2)与x轴成135°的倾斜角.
导数几何意义的实际应用
“菊花”烟火是最壮观的烟花之一,制造时通常期望它在达到最高时爆裂.如果烟花距地面的高度h(m)与时间t(s)之间的关系式为h(t)=-4.9t2+14.7t+18,求烟花在t=2 s时的瞬时速度,并解释烟花升空后的运动状况.
[思路点拨] 烟花在t=2 s时的瞬时速度就是h′(2),即曲线h(t)在点t=2处的切线的斜率;而烟花升空后的运动状况,可以应用切线斜率的变化予以解释.
导数的几何意义是曲线的切线的斜率.反之,在曲线上取确定的点,作曲线的切线,则可以根据切线斜率的符号及绝对值的大小来确定曲线的升降情况及升降的快慢程度.
◎试求过点P(3,5)且与y=x2相切的直线方程.
【错因】 求曲线上的点P处的切线与求过点P的切线有区别,在点P处的切线,点P必为切点;求过点P的切线,点P未必是切点,应注意概念不同,其求法也有所不同.
谢谢观看!
