(人教版)高中数学选修2-2课件:第1章 导数及其应用1.3.1(42张)
文档属性
| 名称 | (人教版)高中数学选修2-2课件:第1章 导数及其应用1.3.1(42张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 15:18:27 | ||
图片预览









文档简介
1.3 导数在研究函数中的应用
1.3.1 函数的单调性与导数
自主学习 新知突破
1.结合实例,直观探索并掌握函数的单调性与导数的关系.
2.能利用导数研究函数的单调性,并能够利用单调性证明一些简单的不等式.
3.会求函数的单调区间(其中多项式函数一般不超过三次).
已知函数f(x)=sin x,其导函数f′(x)=cos x,
[问题3] 试探讨函数的单调性与其导函数正负的关系.
[提示3] 当f′(x)>0时,f(x)为增函数,当f′(x)<0时,f(x)为减函数.
在某个区间(a,b)内,函数的单调性与其导函数的正负有如下关系:
导数与函数的单调性
导数
函数的单调性
f′(x)>0
单调________
f′(x)<0
单调________
f′(x)=0
常数函数
递增
递减
1.确定函数f(x)的__________.
2.求导数f′(x).
3.由f′(x)>0(或f′(x)<0),解出相应的x的范围.当f′(x)>0时,f(x)在相应的区间上是__________;当f′(x)<0时,f(x)在相应的区间上是__________.
4.结合定义域写出单调区间.
利用导数求函数单调区间的基本步骤
定义域
增函数
减函数
利用导数求函数的单调区间注意的问题
(1)在利用导数求函数的单调区间时,首先要确定函数的定义域,解决问题的过程中只能在定义域内,通过讨论导数的符号来判断函数的单调区间.
(2)如果一个函数具有相同单调性的单调区间不止一个,那么这些单调区间中间不能用“∪”连接,而只能用“逗号”或“和”字隔开.
1.函数y=x3-3x的单调减区间是( )
A.(-∞,0) B.(0,+∞)
C.(-1,1) D.(-∞,-1),(1,+∞)
解析: y′=3x2-3,
由y′=3x2-3<0得-1∴函数y=x3-3x的单调减区间是(-1,1).
答案: C
答案: C
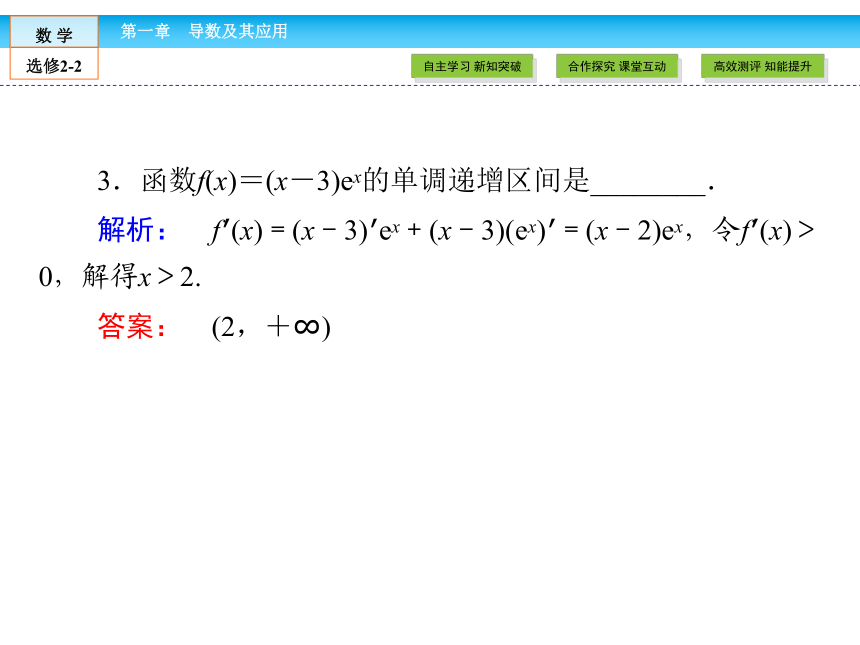
3.函数f(x)=(x-3)ex的单调递增区间是________.
解析: f′(x)=(x-3)′ex+(x-3)(ex)′=(x-2)ex,令f′(x)>0,解得x>2.
答案: (2,+∞)
4.证明函数f(x)=x+sin x在R上是增函数.
证明: f′(x)=1+cos x,
∵-1≤cos x≤1,∴0≤1+cos x≤2,
当且仅当cos x=-1,即x=(2k+1)π(k∈Z)时,f′(x)=0.
∴f(x)=x+sin x在R上是增函数.
合作探究 课堂互动
导数与单调性的关系
如果函数y=f(x)的图象如图所示,那么导函数y=f′(x)的图象可能是( )
[思路点拨] 由函数y=f(x)的图象可得到函数的单调情况,进而确定导数的正负,再“按图索骥”.
解析: 由原函数的单调性可以得到导函数的正负情况依次是正→负→正→负,只有选项A满足.
答案: A
1.利用导数符号判断单调性的方法:
利用导数判断函数的单调性比利用函数单调性的定义简单得多,只需判断导数在该区间内的正负即可.
2.通过图象研究函数单调性的方法:
(1)观察原函数的图象重在找出“上升”“下降”产生变化的点,分析函数值的变化趋势;
(2)观察导函数的图象重在找出导函数图象与x轴的交点,分析导数的正负.
特别提醒:函数的正负与导数的正负没有关系.
1.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)可能为( )
解析: 由函数f(x)的图象知f(x)在(-∞,0)上单调递增,
∴f′(x)>0,故排除A、C.又f(x)在(0,+∞)上有三个单调区间,故排除B,故选D.
答案: D
求函数的单调区间
求下列函数的单调区间:
(1)函数的定义域为R.
y′=2x2-4x=2x(x-2).令y′>0,则2x(x-2)>0,
解得x<0或x>2.
所以函数的单调递增区间为(- ∞,0),(2,+∞).
令y′<0,则2x(x-2)<0,解得0<x<2.
所以函数的单调递减区间为(0,2).
利用导数求函数的单调区间:
(1)求定义域;
(2)解不等式f′(x)>0(或f′(x)<0);
(3)把不等式的解集与定义域求交集得单调区间.
特别提醒:(1)单调区间不能“并”,即不能用“∪”符号连接,只能用“,”或“和”隔开.
(2)导数法求得的单调区间一般用开区间表示.
2.(1)求函数f(x)=3x2-2ln x的单调区间;
(2)设函数f(x)=ln(x+a)+x2,若f′(-1)=0,求a的值,并讨论f(x)的单调区间.
求含参数的函数的单调区间
[思路点拨] 函数解析式中含有参数时,讨论其单调性(或求其单调区间)问题,往往要转化为解含参数的不等式问题,这时应对所含参数进行适当的分类讨论,做到不重不漏,最后要将各种情况分别进行表述.
讨论含有参数的函数的单调性,通常归结为求含参不等式的解集问题,而对含有参数的不等式要针对具体情况进行讨论,但要始终注意定义域对单调性的影响以及分类讨论的标准.
已知函数单调性求参数范围
若函数f(x)=ax3-x2+x-5在R上单调递增,求实数a的取值范围.
1.一般地,已知函数的单调性,如何求参数的取值范围?
2.注意事项:
一般地,最后要检验参数的取值能否使f′(x)恒等于0.若f′(x)恒等于0,则参数的这个值应舍去;若只有在个别点处有f′(x)=0,则由f′(x)≥0(或f′(x)≤0)恒成立解出的参数取值范围为最后解.
4.已知函数f(x)=2ax-x3,x∈(0,1],a>0,若f(x)在(0,1]上是增函数,求a的取值范围.
◎已知函数f(x)=ln(1+x)-x,求f(x)的单调区间.
【错因】 错解的原因是忽视了函数的定义域.本题中含有对数函数,首先应确定函数的定义域,再求导数f′(x),进而判断单调区间.
谢谢观看!
1.3.1 函数的单调性与导数
自主学习 新知突破
1.结合实例,直观探索并掌握函数的单调性与导数的关系.
2.能利用导数研究函数的单调性,并能够利用单调性证明一些简单的不等式.
3.会求函数的单调区间(其中多项式函数一般不超过三次).
已知函数f(x)=sin x,其导函数f′(x)=cos x,
[问题3] 试探讨函数的单调性与其导函数正负的关系.
[提示3] 当f′(x)>0时,f(x)为增函数,当f′(x)<0时,f(x)为减函数.
在某个区间(a,b)内,函数的单调性与其导函数的正负有如下关系:
导数与函数的单调性
导数
函数的单调性
f′(x)>0
单调________
f′(x)<0
单调________
f′(x)=0
常数函数
递增
递减
1.确定函数f(x)的__________.
2.求导数f′(x).
3.由f′(x)>0(或f′(x)<0),解出相应的x的范围.当f′(x)>0时,f(x)在相应的区间上是__________;当f′(x)<0时,f(x)在相应的区间上是__________.
4.结合定义域写出单调区间.
利用导数求函数单调区间的基本步骤
定义域
增函数
减函数
利用导数求函数的单调区间注意的问题
(1)在利用导数求函数的单调区间时,首先要确定函数的定义域,解决问题的过程中只能在定义域内,通过讨论导数的符号来判断函数的单调区间.
(2)如果一个函数具有相同单调性的单调区间不止一个,那么这些单调区间中间不能用“∪”连接,而只能用“逗号”或“和”字隔开.
1.函数y=x3-3x的单调减区间是( )
A.(-∞,0) B.(0,+∞)
C.(-1,1) D.(-∞,-1),(1,+∞)
解析: y′=3x2-3,
由y′=3x2-3<0得-1
答案: C
答案: C
3.函数f(x)=(x-3)ex的单调递增区间是________.
解析: f′(x)=(x-3)′ex+(x-3)(ex)′=(x-2)ex,令f′(x)>0,解得x>2.
答案: (2,+∞)
4.证明函数f(x)=x+sin x在R上是增函数.
证明: f′(x)=1+cos x,
∵-1≤cos x≤1,∴0≤1+cos x≤2,
当且仅当cos x=-1,即x=(2k+1)π(k∈Z)时,f′(x)=0.
∴f(x)=x+sin x在R上是增函数.
合作探究 课堂互动
导数与单调性的关系
如果函数y=f(x)的图象如图所示,那么导函数y=f′(x)的图象可能是( )
[思路点拨] 由函数y=f(x)的图象可得到函数的单调情况,进而确定导数的正负,再“按图索骥”.
解析: 由原函数的单调性可以得到导函数的正负情况依次是正→负→正→负,只有选项A满足.
答案: A
1.利用导数符号判断单调性的方法:
利用导数判断函数的单调性比利用函数单调性的定义简单得多,只需判断导数在该区间内的正负即可.
2.通过图象研究函数单调性的方法:
(1)观察原函数的图象重在找出“上升”“下降”产生变化的点,分析函数值的变化趋势;
(2)观察导函数的图象重在找出导函数图象与x轴的交点,分析导数的正负.
特别提醒:函数的正负与导数的正负没有关系.
1.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)可能为( )
解析: 由函数f(x)的图象知f(x)在(-∞,0)上单调递增,
∴f′(x)>0,故排除A、C.又f(x)在(0,+∞)上有三个单调区间,故排除B,故选D.
答案: D
求函数的单调区间
求下列函数的单调区间:
(1)函数的定义域为R.
y′=2x2-4x=2x(x-2).令y′>0,则2x(x-2)>0,
解得x<0或x>2.
所以函数的单调递增区间为(- ∞,0),(2,+∞).
令y′<0,则2x(x-2)<0,解得0<x<2.
所以函数的单调递减区间为(0,2).
利用导数求函数的单调区间:
(1)求定义域;
(2)解不等式f′(x)>0(或f′(x)<0);
(3)把不等式的解集与定义域求交集得单调区间.
特别提醒:(1)单调区间不能“并”,即不能用“∪”符号连接,只能用“,”或“和”隔开.
(2)导数法求得的单调区间一般用开区间表示.
2.(1)求函数f(x)=3x2-2ln x的单调区间;
(2)设函数f(x)=ln(x+a)+x2,若f′(-1)=0,求a的值,并讨论f(x)的单调区间.
求含参数的函数的单调区间
[思路点拨] 函数解析式中含有参数时,讨论其单调性(或求其单调区间)问题,往往要转化为解含参数的不等式问题,这时应对所含参数进行适当的分类讨论,做到不重不漏,最后要将各种情况分别进行表述.
讨论含有参数的函数的单调性,通常归结为求含参不等式的解集问题,而对含有参数的不等式要针对具体情况进行讨论,但要始终注意定义域对单调性的影响以及分类讨论的标准.
已知函数单调性求参数范围
若函数f(x)=ax3-x2+x-5在R上单调递增,求实数a的取值范围.
1.一般地,已知函数的单调性,如何求参数的取值范围?
2.注意事项:
一般地,最后要检验参数的取值能否使f′(x)恒等于0.若f′(x)恒等于0,则参数的这个值应舍去;若只有在个别点处有f′(x)=0,则由f′(x)≥0(或f′(x)≤0)恒成立解出的参数取值范围为最后解.
4.已知函数f(x)=2ax-x3,x∈(0,1],a>0,若f(x)在(0,1]上是增函数,求a的取值范围.
◎已知函数f(x)=ln(1+x)-x,求f(x)的单调区间.
【错因】 错解的原因是忽视了函数的定义域.本题中含有对数函数,首先应确定函数的定义域,再求导数f′(x),进而判断单调区间.
谢谢观看!
