河南省商开大联考2020-2021学年高二下学期期中考试数学(文)试题 Word版含答案
文档属性
| 名称 | 河南省商开大联考2020-2021学年高二下学期期中考试数学(文)试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1005.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 00:00:00 | ||
图片预览




文档简介
商开大联考2020~2021学年下学期期中考试
高二数学(文科)
考生须知:
本试卷满分120分,考试时间为120分钟.
答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确粘贴在条形码区域内.
请按照题号顺序在答题卡各题目的区域内作答,超出答题区域的答案无效;在草稿纸上、试题纸上答案无效.
选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.
保持卡面整洁,不要折叠、不要弄脏、弄皱,不准使用涂改液、刮纸刀.
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若false(false是虚数单位),则在复平面内false对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 复数的知识结构图如图所示,其中false四个方格中的内容分别为( )
A.实数.纯虚数、无理数、有理数
B实数、虚数、负实数、正实数
C.实数、虚数、无理数、有理数
D.实数、虚数、有理数、无理数
3. 河南师范大学数学与信息科学学院前身是始建于1923年的中州大学(原河南大学的前身)的数理系和创建于1951年的平原师范学院数学系,是河南师范大学设立最早的院系之一,2000年根据人才培养和学科专业建设的需要撤销数学系,组建数学与信息科学学院,简称数科院,该学院2020年毕业生就业率高达100%.关于数科院2020届一班的学生,有下列三个说法:
①安梦琦是数科院2020届一班的毕业生;
②安梦琦目前从事中学数学教育教学工作;
③数科院2020届一班的毕业生目前都从事中学数学教育教学工作.
将这三个说法写一个“三段论”形式的推理,则大前提、小前提和结论依次为( )
A.②①③ B.②③① C.③②① D. ③①②
4. 观察下图中图形的规律,最适合填入问号处的是( )
A. B.
C. D.
5. 用反证法证明命题“若关于false的一元二次方程false有有理根,那么false中至少又一个偶数”时.下列假设正确的是( )
A.假设false都是偶数 B.假设false都不是偶数
C. 假设false最多有一个是偶数 D.假设false最多有两个是偶数
6. 2020年12月初某超市与蔬菜种植户签订进货合同,以false元/千克的单价购进一批大葱,并且每天都以不同的价格投放市场,经过一个月的市场营销,得到该批大葱每天的销售量false(千克)与大葱的销售单价false(元/千克)的情况如下:
false
false
false
false
false
false
false
false
false
false
false
false
false
false
由表中数据计算出线性回归方程false中的false.若该超市将某一天大葱的销售价格定为false元/千克时,则该超市这天销售大葱获得的利润估计为( )
A.false B.false C. false D.false
7. 给出下列四个命题:
①若复数false满足士∈R,则false;
②若复数false满足false,则false;
③若复数false满足false,则false互为共扼复数;
④若复数false满足false是虚数false不是false的共扼复数.
其中真命题的个数是( )
A.false B.false C. false D.false
8.在数列false中,若false,则false等于( )
A.false B.false C. false D.false
9. 在证明命题“对任意两个实数false,若false,则false的取值范围是false”时,我们可以构造函数false,因为false,所
以false对任意实数false都成立,所以false,所以false,则false的取值范围是false,类比上述的方法,若false个实数false满足false时,能得到false的取值范围是( )
A.false B.false
C. false D.false
10. 若复数false的模为false,则false的取值范围是( )
A.false B.false C.false D.false
11. 对于任意实数false,符号false表示不超过false的最大整数,如false,函数false叫做“取整函数”,也叫做高斯(false)函数.这个函数在数学本身和生产实践中都有广泛的应用.小明利用学习过的对数知识,发现:false,对应的false是一个false位数,false是一个false位数,依此规律,若false,且false,则false是( )
A.一位数 B.两位数 C.三位数 D.四位数
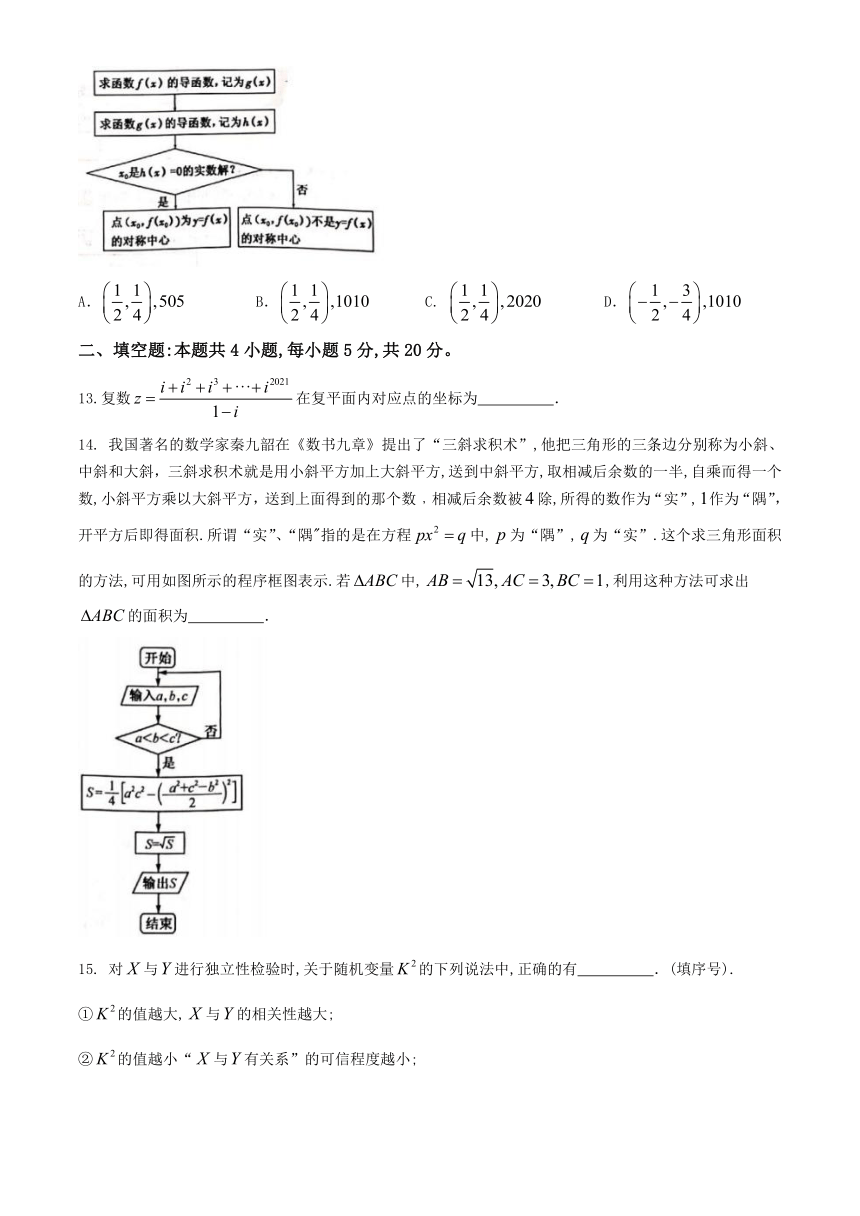
12. 研究发现,任意一个三次函数false的图象必有一个对称中心.一般地,判断点false是否是三次函数false图象的对称中心的流程如图所示,对于函数falsefalse,其图象的对称中心以及false的值分别是( )
A.false B.false C. false D.false
二、填空题:本题共4小题,每小题5分,共20分。
13.复数false在复平面内对应点的坐标为 .
14. 我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”,他把三角形的三条边分别称为小斜、中斜和大斜,三斜求积术就是用小斜平方加上大斜平方,送到中斜平方,取相减后余数的一半,自乘而得一个数,小斜平方乘以大斜平方,送到上面得到的那个数﹐相减后余数被false除,所得的数作为“实”,false作为“隅”,开平方后即得面积.所谓“实”、“隅"指的是在方程false中,false为“隅”,false为“实”.这个求三角形面积的方法,可用如图所示的程序框图表示.若false中,false,利用这种方法可求出false的面积为 .
15. 对false与false进行独立性检验时,关于随机变量false的下列说法中,正确的有 .(填序号).
①false的值越大,false与false的相关性越大;
②false的值越小“false与false有关系”的可信程度越小;
③若求出false,则有false的把握认为“false与false有关系”,即“false与false有关系”的推断出现错误的概率不会超过false;
④在false列联表中,若每个数据变为原来的false倍,则false的值变为原来的false倍.
附:false
false
false
false
false
false
false
false
false
16. 有一个游戏:将分别标有“恭”“喜”“发"“财”的四张卡片随机发给张、王、李、赵false个人,每人一张,这false个人在看过自己的卡片上标的字之后,张说:王或李拿到了标有“发”的卡片;王说:张或李拿到了标有“喜”的卡片;李说:标有“恭”的卡片在张手中;赵说:张拿到了标有“发”的卡片.如果张、王、李、赵false个人说的都是假话,那么张、王、李,赵false个人拿到卡片上的字依次为 .
三解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
17. 已知false是虚数,false是实数.
false求false
false若false的实部与虚部相同,求false.
18. 高中阶段有这样一句话,成也数学败也数学,意思是说数学成绩好的同学总成绩也好,数学成绩不好的同学总成绩也不好.某市教育局对本届高三学生的上学期期末考试成绩进行随机调查得到如下false列联表:
总成绩好false
总成绩不好
总计
数学成绩好
false
false
false
数学成绩不好
false
false
false
总计
false
false
false
false求表中false的值;
false能否有false的把握认为学生总成绩不好与数学成绩不好有关?
附:false
false
false
false
false
false
false
false
false
false
false
19. false若false都是正数,且false.求false的最小值;
false若false是不相等的实数,证明:false
20. 某集团商品的推销员每年推销商品的件粉(件)往往与推销员从事推销工作的年数false(年)有关,该集团人事部随机调研了集团内false推销吊每年推销商品的件数false(件)与推销员从事推销工作的年数false(年),得到一组数据如下.
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false利用相关系数false判断false与false之间相关关系的强弱(若false,则false与false间相关关系强,否则相关关系弱);
false求线性回归直线方程false
false预测从事推销工作false年的推销员推销商品的件数会不会比从事推销工作false年的推销员推销商品的件数的false倍还要多?
附:①false
②相关系数false
③回归直线方程false中,false
21. 已知椭圆false,点false在圆false上,圆false在点false处的切线false与椭圆false相交于false两点,试用反证法证明:以false为直径的圆不过坐标原点.
(二)选考题:共10分。请考生在第22,23两题中任选一题作答。如果多做,则按所做的第一题计分。
22.选修4-4;坐标系与参数方程在平面直角坐标系false中,曲线false(false是参数).以false为极点,false轴的正半轴为极轴建立极坐标系,直线false的极坐标方程为false
false求曲线false的普通方程以及直线false的直角坐标方程;
false设false,直线false与曲线false交于false两点,求false的值.
23.选修4-5:不等式选讲
已知函数false
false解不等式false
false若false对任意实数false都成立,求实数false的最小值.
商开大联考2020~2021学年下学期期中考试·高二数学(文科)
参考答案、提示及评分细则
1.false 因为false,故false在复平面内对应的点在第一象限.故选false.
2.false 由复数与实数、整数、分数的包含关系知false正确.故选false.
3.false 根据三段论推理的形式“大前提,小前提,结论”,以及大前提、小前提和结论的关系,可知选false.
4.false 黑点和白点排成false行false列,规律是每一行中都是false黑false白.故选false.
5.false false,false,false中存在偶数,反面就是false,false,false中没有偶数,即都不是偶数.故选false.
6.false 因为false,false,
所以false,解得false,
所以false(元/千克)时false(千克),falsefalse(元).故选false.
7.false 对于①,设复数false(false,false),则false,
若false,则false,所以false,故①为真命题;
对于②,若复数false,则false,但false,故②为假命题;
对于③,若复数false,false满足false,但false,故③为假命题;
对于④,若false和false是共轭复数,则false为实数,不会为虚数,故④为真命题.故选false.
8.false 因为false,false,
所以false,false,false,false,false,…,
由此可归纳得到false(false,false),
所以false.故选false.
9.false 令false,
由于对一切实数false,恒有false,所以false,
所以false.故选false.
10.false 因为复数false(false,false)的模为false,
所以false(false,false).
又false表示半圆false(false,false)上的动点false与定点false连线的斜率,
如图,过点false作半圆false的切线false,切点为false,
在直角false中,false,false,false,falsefalse,
所以false.故选false.
11.false 因为falsefalsefalse,false,即false,
所以false是一个两位数,
所以false是两位数.故选false.
12.false 因为false,
所以false,false,
令false,解得false,又false,
所以三次曲线false的对称中心是false,则false.
所以false,
于是false.故选false.
13.false 因为false,而false,
所以false,false,
故false对应的点的坐标为false.
14.false 根据程序框图直接将false,false,false代入false,
得false,执行下一步,得false,故输出false的值为false.
15.②③④ false的值越大,说明有更大的把握认为false与false有关系,但却不能判断其相关性大小,故①错,②③正确;对于④,若false列联表中,若每个数据变为原来的false倍,则false的值变为
false是原来的false倍,所以④正确.
16.财,喜,恭,发 由张、赵说假话可得赵拿到标有“发”的卡片,由王说假话可得王拿到标有“喜”的卡片,由李说假话可知张拿到标有“财”的卡片,故李拿到标有“恭”的卡片,即张、王、李、赵false个人拿到卡片上的字依次为财,喜,恭,发.
17.解:(1)设false(false,false且false),则
false.
因为false是实数,
所以false.
又因为false,
所以false,false.
(2)因为false的实部与虚部相同,
所以false.
与false联立,解得false或false
所以false或false.
18.解:(1)由false,得false.
由false,得false.
由false,得false.
由false,得false.
注:false,false,false,false的值,求对三个给5分,求对两个给3分,只求对一个给2分.
(2)因为false,
因此有false的把握认为学生总成绩不好与数学成绩不好有关.
19.(1)解:因为false,false都是正数且false,
所以false,当且仅当false时等号成立.
所以false时,false的最小值为false.
(2)证明:若false,则false显然成立;
若false,要证明false,
只要证明false,
只要证明false,即证false,
因为false,
所以false成立,
所以当false时,原不等式也成立.
综上所述,原不等式成立.
20.解:(1)因为false,false,false.
所以false与false之间具有很强的相关关系.
(2)false,false.
故回归直线方程为false.
(3)因为false时,false;false时,false;由于false,
所以可以预测从事推销工作10年的推销员推销商品的件数比从事推销工作2年的推销员推销商品的件数的false倍还要多.
21.证明:假设以false为直径的圆过原点,则false.
当直线false的斜率不存在时,直线false的方程是:false或false,直线false与椭圆false:false的交点是false,false或false,false,
falsefalse,
false当直线false的斜率不存在时,假设不成立.
当直线false的斜率存在时,设直线false的方程是false,
联立false消去false,并整理得false.
false直线false与椭圆false相交于false,false两点,
falsefalse,化简得false.
设false,false,则false,false,
false.
falsefalse,
falsefalse,
falsefalse①
又false直线false与圆false相切,
falsefalse,
falsefalse②,
解①②得false,这是不可能的.
false当直线false的斜率存在时,假设也不成立.
false无论直线false的斜率是否存在,假设都不成立,
∴以false为直径的圆不过原点.
22.解:(1)由false得false
所以false,即曲线false的普通方程是false.
由false,得false,
又false,false,
所以false,即直线false的直角坐标方程为false.
(2)因为直线false经过点false,且倾斜角是false,
所以直线false的参数方程是false(false是参数).
设false,false对应的参数分别为false,false,
将直线false的参数方程代入false,整理得false,
所以false,false.
所以false.
23.解:(1)因为false
由false,得false或false或false解得false,
所以不等式false的解集是false.
(2)因为对任意实数false都有false,
所以false,
所以实数false的最小值是false.
高二数学(文科)
考生须知:
本试卷满分120分,考试时间为120分钟.
答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚,将“条形码”准确粘贴在条形码区域内.
请按照题号顺序在答题卡各题目的区域内作答,超出答题区域的答案无效;在草稿纸上、试题纸上答案无效.
选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.
保持卡面整洁,不要折叠、不要弄脏、弄皱,不准使用涂改液、刮纸刀.
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若false(false是虚数单位),则在复平面内false对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 复数的知识结构图如图所示,其中false四个方格中的内容分别为( )
A.实数.纯虚数、无理数、有理数
B实数、虚数、负实数、正实数
C.实数、虚数、无理数、有理数
D.实数、虚数、有理数、无理数
3. 河南师范大学数学与信息科学学院前身是始建于1923年的中州大学(原河南大学的前身)的数理系和创建于1951年的平原师范学院数学系,是河南师范大学设立最早的院系之一,2000年根据人才培养和学科专业建设的需要撤销数学系,组建数学与信息科学学院,简称数科院,该学院2020年毕业生就业率高达100%.关于数科院2020届一班的学生,有下列三个说法:
①安梦琦是数科院2020届一班的毕业生;
②安梦琦目前从事中学数学教育教学工作;
③数科院2020届一班的毕业生目前都从事中学数学教育教学工作.
将这三个说法写一个“三段论”形式的推理,则大前提、小前提和结论依次为( )
A.②①③ B.②③① C.③②① D. ③①②
4. 观察下图中图形的规律,最适合填入问号处的是( )
A. B.
C. D.
5. 用反证法证明命题“若关于false的一元二次方程false有有理根,那么false中至少又一个偶数”时.下列假设正确的是( )
A.假设false都是偶数 B.假设false都不是偶数
C. 假设false最多有一个是偶数 D.假设false最多有两个是偶数
6. 2020年12月初某超市与蔬菜种植户签订进货合同,以false元/千克的单价购进一批大葱,并且每天都以不同的价格投放市场,经过一个月的市场营销,得到该批大葱每天的销售量false(千克)与大葱的销售单价false(元/千克)的情况如下:
false
false
false
false
false
false
false
false
false
false
false
false
false
false
由表中数据计算出线性回归方程false中的false.若该超市将某一天大葱的销售价格定为false元/千克时,则该超市这天销售大葱获得的利润估计为( )
A.false B.false C. false D.false
7. 给出下列四个命题:
①若复数false满足士∈R,则false;
②若复数false满足false,则false;
③若复数false满足false,则false互为共扼复数;
④若复数false满足false是虚数false不是false的共扼复数.
其中真命题的个数是( )
A.false B.false C. false D.false
8.在数列false中,若false,则false等于( )
A.false B.false C. false D.false
9. 在证明命题“对任意两个实数false,若false,则false的取值范围是false”时,我们可以构造函数false,因为false,所
以false对任意实数false都成立,所以false,所以false,则false的取值范围是false,类比上述的方法,若false个实数false满足false时,能得到false的取值范围是( )
A.false B.false
C. false D.false
10. 若复数false的模为false,则false的取值范围是( )
A.false B.false C.false D.false
11. 对于任意实数false,符号false表示不超过false的最大整数,如false,函数false叫做“取整函数”,也叫做高斯(false)函数.这个函数在数学本身和生产实践中都有广泛的应用.小明利用学习过的对数知识,发现:false,对应的false是一个false位数,false是一个false位数,依此规律,若false,且false,则false是( )
A.一位数 B.两位数 C.三位数 D.四位数
12. 研究发现,任意一个三次函数false的图象必有一个对称中心.一般地,判断点false是否是三次函数false图象的对称中心的流程如图所示,对于函数falsefalse,其图象的对称中心以及false的值分别是( )
A.false B.false C. false D.false
二、填空题:本题共4小题,每小题5分,共20分。
13.复数false在复平面内对应点的坐标为 .
14. 我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”,他把三角形的三条边分别称为小斜、中斜和大斜,三斜求积术就是用小斜平方加上大斜平方,送到中斜平方,取相减后余数的一半,自乘而得一个数,小斜平方乘以大斜平方,送到上面得到的那个数﹐相减后余数被false除,所得的数作为“实”,false作为“隅”,开平方后即得面积.所谓“实”、“隅"指的是在方程false中,false为“隅”,false为“实”.这个求三角形面积的方法,可用如图所示的程序框图表示.若false中,false,利用这种方法可求出false的面积为 .
15. 对false与false进行独立性检验时,关于随机变量false的下列说法中,正确的有 .(填序号).
①false的值越大,false与false的相关性越大;
②false的值越小“false与false有关系”的可信程度越小;
③若求出false,则有false的把握认为“false与false有关系”,即“false与false有关系”的推断出现错误的概率不会超过false;
④在false列联表中,若每个数据变为原来的false倍,则false的值变为原来的false倍.
附:false
false
false
false
false
false
false
false
false
16. 有一个游戏:将分别标有“恭”“喜”“发"“财”的四张卡片随机发给张、王、李、赵false个人,每人一张,这false个人在看过自己的卡片上标的字之后,张说:王或李拿到了标有“发”的卡片;王说:张或李拿到了标有“喜”的卡片;李说:标有“恭”的卡片在张手中;赵说:张拿到了标有“发”的卡片.如果张、王、李、赵false个人说的都是假话,那么张、王、李,赵false个人拿到卡片上的字依次为 .
三解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
17. 已知false是虚数,false是实数.
false求false
false若false的实部与虚部相同,求false.
18. 高中阶段有这样一句话,成也数学败也数学,意思是说数学成绩好的同学总成绩也好,数学成绩不好的同学总成绩也不好.某市教育局对本届高三学生的上学期期末考试成绩进行随机调查得到如下false列联表:
总成绩好false
总成绩不好
总计
数学成绩好
false
false
false
数学成绩不好
false
false
false
总计
false
false
false
false求表中false的值;
false能否有false的把握认为学生总成绩不好与数学成绩不好有关?
附:false
false
false
false
false
false
false
false
false
false
false
19. false若false都是正数,且false.求false的最小值;
false若false是不相等的实数,证明:false
20. 某集团商品的推销员每年推销商品的件粉(件)往往与推销员从事推销工作的年数false(年)有关,该集团人事部随机调研了集团内false推销吊每年推销商品的件数false(件)与推销员从事推销工作的年数false(年),得到一组数据如下.
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false利用相关系数false判断false与false之间相关关系的强弱(若false,则false与false间相关关系强,否则相关关系弱);
false求线性回归直线方程false
false预测从事推销工作false年的推销员推销商品的件数会不会比从事推销工作false年的推销员推销商品的件数的false倍还要多?
附:①false
②相关系数false
③回归直线方程false中,false
21. 已知椭圆false,点false在圆false上,圆false在点false处的切线false与椭圆false相交于false两点,试用反证法证明:以false为直径的圆不过坐标原点.
(二)选考题:共10分。请考生在第22,23两题中任选一题作答。如果多做,则按所做的第一题计分。
22.选修4-4;坐标系与参数方程在平面直角坐标系false中,曲线false(false是参数).以false为极点,false轴的正半轴为极轴建立极坐标系,直线false的极坐标方程为false
false求曲线false的普通方程以及直线false的直角坐标方程;
false设false,直线false与曲线false交于false两点,求false的值.
23.选修4-5:不等式选讲
已知函数false
false解不等式false
false若false对任意实数false都成立,求实数false的最小值.
商开大联考2020~2021学年下学期期中考试·高二数学(文科)
参考答案、提示及评分细则
1.false 因为false,故false在复平面内对应的点在第一象限.故选false.
2.false 由复数与实数、整数、分数的包含关系知false正确.故选false.
3.false 根据三段论推理的形式“大前提,小前提,结论”,以及大前提、小前提和结论的关系,可知选false.
4.false 黑点和白点排成false行false列,规律是每一行中都是false黑false白.故选false.
5.false false,false,false中存在偶数,反面就是false,false,false中没有偶数,即都不是偶数.故选false.
6.false 因为false,false,
所以false,解得false,
所以false(元/千克)时false(千克),falsefalse(元).故选false.
7.false 对于①,设复数false(false,false),则false,
若false,则false,所以false,故①为真命题;
对于②,若复数false,则false,但false,故②为假命题;
对于③,若复数false,false满足false,但false,故③为假命题;
对于④,若false和false是共轭复数,则false为实数,不会为虚数,故④为真命题.故选false.
8.false 因为false,false,
所以false,false,false,false,false,…,
由此可归纳得到false(false,false),
所以false.故选false.
9.false 令false,
由于对一切实数false,恒有false,所以false,
所以false.故选false.
10.false 因为复数false(false,false)的模为false,
所以false(false,false).
又false表示半圆false(false,false)上的动点false与定点false连线的斜率,
如图,过点false作半圆false的切线false,切点为false,
在直角false中,false,false,false,falsefalse,
所以false.故选false.
11.false 因为falsefalsefalse,false,即false,
所以false是一个两位数,
所以false是两位数.故选false.
12.false 因为false,
所以false,false,
令false,解得false,又false,
所以三次曲线false的对称中心是false,则false.
所以false,
于是false.故选false.
13.false 因为false,而false,
所以false,false,
故false对应的点的坐标为false.
14.false 根据程序框图直接将false,false,false代入false,
得false,执行下一步,得false,故输出false的值为false.
15.②③④ false的值越大,说明有更大的把握认为false与false有关系,但却不能判断其相关性大小,故①错,②③正确;对于④,若false列联表中,若每个数据变为原来的false倍,则false的值变为
false是原来的false倍,所以④正确.
16.财,喜,恭,发 由张、赵说假话可得赵拿到标有“发”的卡片,由王说假话可得王拿到标有“喜”的卡片,由李说假话可知张拿到标有“财”的卡片,故李拿到标有“恭”的卡片,即张、王、李、赵false个人拿到卡片上的字依次为财,喜,恭,发.
17.解:(1)设false(false,false且false),则
false.
因为false是实数,
所以false.
又因为false,
所以false,false.
(2)因为false的实部与虚部相同,
所以false.
与false联立,解得false或false
所以false或false.
18.解:(1)由false,得false.
由false,得false.
由false,得false.
由false,得false.
注:false,false,false,false的值,求对三个给5分,求对两个给3分,只求对一个给2分.
(2)因为false,
因此有false的把握认为学生总成绩不好与数学成绩不好有关.
19.(1)解:因为false,false都是正数且false,
所以false,当且仅当false时等号成立.
所以false时,false的最小值为false.
(2)证明:若false,则false显然成立;
若false,要证明false,
只要证明false,
只要证明false,即证false,
因为false,
所以false成立,
所以当false时,原不等式也成立.
综上所述,原不等式成立.
20.解:(1)因为false,false,false.
所以false与false之间具有很强的相关关系.
(2)false,false.
故回归直线方程为false.
(3)因为false时,false;false时,false;由于false,
所以可以预测从事推销工作10年的推销员推销商品的件数比从事推销工作2年的推销员推销商品的件数的false倍还要多.
21.证明:假设以false为直径的圆过原点,则false.
当直线false的斜率不存在时,直线false的方程是:false或false,直线false与椭圆false:false的交点是false,false或false,false,
falsefalse,
false当直线false的斜率不存在时,假设不成立.
当直线false的斜率存在时,设直线false的方程是false,
联立false消去false,并整理得false.
false直线false与椭圆false相交于false,false两点,
falsefalse,化简得false.
设false,false,则false,false,
false.
falsefalse,
falsefalse,
falsefalse①
又false直线false与圆false相切,
falsefalse,
falsefalse②,
解①②得false,这是不可能的.
false当直线false的斜率存在时,假设也不成立.
false无论直线false的斜率是否存在,假设都不成立,
∴以false为直径的圆不过原点.
22.解:(1)由false得false
所以false,即曲线false的普通方程是false.
由false,得false,
又false,false,
所以false,即直线false的直角坐标方程为false.
(2)因为直线false经过点false,且倾斜角是false,
所以直线false的参数方程是false(false是参数).
设false,false对应的参数分别为false,false,
将直线false的参数方程代入false,整理得false,
所以false,false.
所以false.
23.解:(1)因为false
由false,得false或false或false解得false,
所以不等式false的解集是false.
(2)因为对任意实数false都有false,
所以false,
所以实数false的最小值是false.
同课章节目录
