六年级下册数学课件-整理与复习 人教版(共79张ppt)
文档属性
| 名称 | 六年级下册数学课件-整理与复习 人教版(共79张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 15:37:05 | ||
图片预览










文档简介
整理与复习
通过整理复习,进一步巩固认识圆柱和圆锥的特征以及他们之间的联系。
熟练掌握圆柱表面积、体积和圆锥体积的计算方法。
进一步发展空间观念,提高解决实际问题的能力。
教学目标
圆柱、圆锥表面积、体积的计算。
圆柱、圆锥的特征和它们的体积之间的联系与区别。
教学重点
教学难点
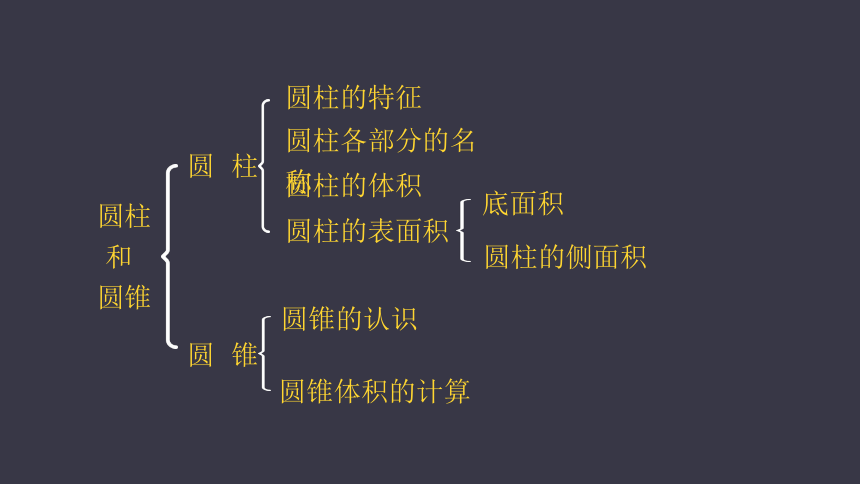
圆 锥
圆锥的认识
圆锥体积的计算
圆 柱
圆柱的体积
底面积
圆柱的表面积
圆柱的侧面积
圆柱的特征
圆柱各部分的名称
圆柱?
?和?
圆锥
1、圆柱与圆锥各有哪些特征?
2、怎样求圆柱的侧面积.表面积.体积?
计算公式各是什么?
3、怎样求圆锥的体积?计算公式是什么?
4、圆柱与圆锥的体积之间有什么系?
1、圆柱与圆锥各有哪些特征?
2、怎样求圆柱的侧面积.表面积.体积?计算公式各是什么?
3、怎样求圆锥的体积?计算公式是什么?
4、圆柱与圆锥的体积之间有什么系?
圆
柱?
和?
圆?
锥
圆柱的认识
圆柱的表面积
圆柱的体积
圆锥的认识
圆锥的体积
组成:
特征:
两个底面、一个侧面。
底面是完全相同的两个圆;侧面是曲面,展开是一个长方形(或正方形);圆柱有无数条高。
S侧=ch=2πrh=πdh
S=S侧+2S底
组成:
特征:底面是一个圆;侧面是曲面,展开是一个扇形;圆锥只有一条高。
一个底面,一个侧面。
知识整理
知识整理
类别
特 征
表面积
体 积
关 系
形 成
圆
柱
圆
锥
1个侧面(曲面)2个底面(圆形)无数条高上下粗细一样
1个顶点
1个侧面(曲面)
1个底面(圆形)?
1条高
体积是等底
等高的圆锥
体积的3倍
体积是等底等高的圆柱
体积的
V=sh
S=
圆柱的特征:
知识整理
1.两个底面是半径相等的两个圆
2.圆柱有一个曲面叫做侧面,沿高展开后是
一个长方形(或正方形)。
3.圆柱有无数条高,且高的长度都相等
长=底面周长
宽=高
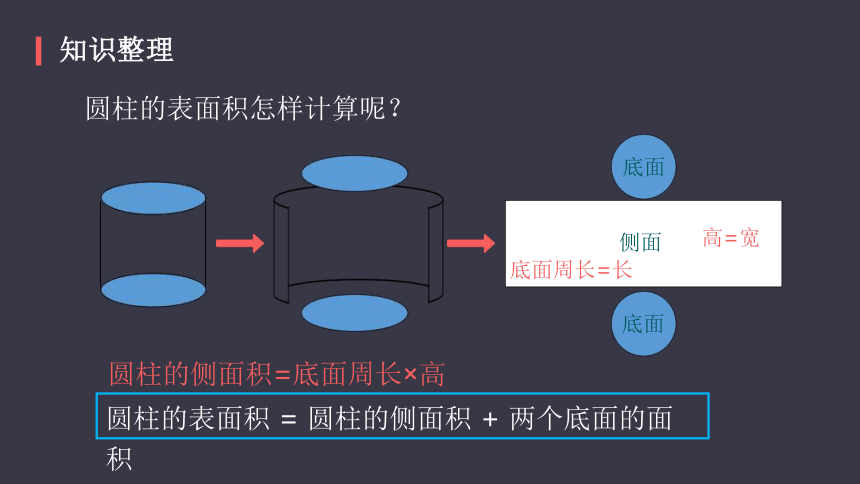
圆柱的表面积怎样计算呢?
知识整理
圆柱的侧面积=底面周长×高
底面
底面
侧面
底面周长=长
高=宽
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
高等于圆柱的 高 。
长方体的底面积等于圆柱的 底面积 ,
长方体体积=底面积×高
圆柱体积
=底面积×高
V=Sh
||
知识整理
圆锥的特征:
知识整理
1.圆锥的底面是一个圆
2.圆锥的侧面是一个曲面,
展开后是一个扇形
3.圆锥只有一个顶点,一条高。
(从顶点到底面圆心的距离是圆锥的高)
圆柱侧面积=底面周长×高
圆柱表面积=侧面积+底面积×2
圆 柱 体积=底面积×高
圆 锥 体积=底面积×高÷3
基
本
公
式
知识整理
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的三分之一
等底等高圆柱体积是圆锥体积的3倍
知识整理
等底等高的圆柱和圆锥体积有以下关系:
柱锥关系
规律:等底等高的圆柱和圆锥体积:锥1、差2、柱3、和4
(1)圆锥体积是圆柱的
(2)圆柱体积是圆锥的3倍
(3)圆锥体积比圆柱少
(4)圆柱体积比圆锥多2倍
等底等高
柱锥关系
V柱=
3V锥
你知道圆柱和圆锥是啥关系吗?
V柱=45立方厘米 V锥=?立方厘米
V柱= ? ? ? 立方厘米 ? ? ? ?V锥=24立方厘米
柱锥关系
S? ? ? ? ? ? ? ? =? ? ? ? ? ? ? ? ?S
?
72
圆柱与圆锥的关系
1、圆柱与圆锥的体积,底面积相等,则圆柱的高是圆锥高得 ? ? ?,圆锥的高是圆柱高的3倍。
2、圆柱与圆锥的体积,高相等,则圆柱的底面积是圆锥底面积得 ? ? ?,圆锥的底面积是圆柱底面积的3倍。
柱锥关系
等积等底
柱锥关系
h柱=18分米 ? ? ? ? ? ? ? ? ?h锥= ? ? 分米
54
?
你知道圆柱和圆锥是啥关系吗?
h柱= ? ? ?分米 ? ? ? ? ?h锥=42分米
柱锥关系
14
?
等积等高
S柱=18平方分米 ? ? ? ? ?S锥= ? ? ?平方分米
你知道圆柱和圆锥是啥关系吗?
柱锥关系
V ? ? ? ? ? ? ? ? ?= ? ? ? ? ? ? ? ? V
54
?
V? ? ? ? ? ? ? ? ?= ? ? ? ? ? ? ? ? V
S柱= ? ? ?平方分米 ? ? ? ? ? ?S锥=27平方分米
9
?
柱锥关系
1.将下面图形分类。说说每类图形的名称和特征。
整理与复习
图1
图2
图3
图4
图5
图6
圆柱
圆锥
圆柱:图中第1、2、6、幅图是圆柱。其特征是圆柱的两个底面都是圆,并且大小相同;圆柱的侧面是曲面,侧面沿高展开后是一个长方形(或正方形);圆柱有无数条高,长度都相等。
圆锥:第3、4、5幅图是圆锥。其特征是圆锥的底面是一个圆;侧面是一个曲面,侧面展开后是一个扇形;圆锥只有一条高(顶点到底面圆心的距离)。
整理与复习
2.想一想 圆柱的侧面积、表面积怎样计算?圆锥的体积公式是怎样导出的?在填写下表。
整理与复习
圆柱的侧面积=底面周长×高圆柱的表面积=圆柱的侧面积+两个底面积圆柱的体积公式是把它转化成长方体而推导出来的;
圆锥的体积是通过装水和沙试验推导出来的。
圆柱表面积用字母表示为:
S表= S侧+2S底
圆柱侧面积用字母表示为:
整理与复习
直接计算:S侧=Ch
利用直径计算:
利用半径计算:
运用圆柱的表面积公式解决实际问题时,并不是所有的圆柱形物体都有两个底面,有的没有底面,要根据实际情况选择合理的解题方法。
圆柱体积用字母表示为:
圆锥体积用字母表示为:
整理与复习
无论是求圆柱的表面积还是体积,如果给底面直径或周长要先求出半径。侧面积可以直接用公式求。
求圆锥的体积不要忘记乘
整理与复习
名称
半径
直径
高
表面积
体积
圆柱
圆锥
5dm
1m
20cm
2dm
0.5m
10dm
2m
40cm
4dm
1m
4dm
0.7m
5cm
2.4dm
4.5m
3.妈妈给小雨的塑料壶做了一个布套(如图)小雨每天上学带一壶水。
(1)至少用了多少布料?
(2)小雨在学校一天喝1.5L的水,这壶水够喝吗?(水壶的厚度忽略不计。)
整理与复习
分析:求所用布料就是求水壶的表面积,求能装多少水即求水壶的体积。
(1)3.14×10×20+2×3.14 ×(10÷2)
整理与复习
答:布料使用面积为
(2) 3.14×(10÷2)
1.57L>1.5L
答:这壶水够喝。
4.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。底面直径是4dm,圆柱高2dm,圆锥高4dm, 每立方分米稻谷重0.65kg。
(1)这个漏斗最多能装多少千克稻谷?
(2)如果稻谷的出米率是70%,一漏斗能磨多少大米?
整理与复习
答:这个漏斗最多能装? ? ? ? ? 千克稻谷。
答:一漏斗稻谷能磨? ? ? ? ? ? ?千克大米。
整理与复习
分析:漏斗是由一个圆柱和一个圆锥组合而成的。
1、把一块长方体钢坯铸造成一根直径为4dm的圆柱形钢筋,求钢筋的长度。
练习七
分析:等积变形题。长方体的体积和圆柱的体积相等,钢筋的长度(圆柱的高)等于求出长方体的体积除以圆柱的底面积。
长方体的体积(圆柱的体积):12.56×5×4=251.2(立方分米)
圆柱的底面积: 3.14 ×(4÷2)
钢筋的长度:251.2÷12.56=20(分米)
答:钢筋的长度是20分米。
2. 一个圆锥形沙堆,底面积是28.26m ?,高是2.5m。用这堆 沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
2
练习七
分析:首先要明确公路的形状是一个近似的长方体,圆锥形
沙堆的体积等于长方体的体积。还要注意单位换算。
2cm=0.02m
(长=长方体的体积÷宽÷高)
沙堆的体积:?
所铺公路的长度:
23.55÷10÷0.02=2.355÷0.02
=117.75(米)
答:能铺117.75米。
=9.42×2.5
=23.55(立方米)
3、一块蜂窝煤如图所示。做一块蜂窝煤大约需要煤多少立方分米?
练习七
分析:蜂窝煤的体积等于大圆柱的体积减去12个中空的小圆柱的体积。
3.14×(12÷2) ×9- 3.14×(2÷2) ×9×12
=1017.36-339.12
=678.24(立方厘米)
=0.67824(立方分米)
答:做一块蜂窝煤大约需要煤0.67824立方分米。
2
2
4、有块正方体的木料,它的棱长是4dm。把这块木料加工成一个最大的圆柱体(如图)。这个圆柱的体积是多少?
练习七
3.14×(4÷2) ×4=50.24(立方分米)
答:这个圆柱体的体积是50.24立方分米。
2
5、一支120ml的牙膏管口的直径为5mm,李叔叔每天刷牙2次,每次挤出的牙膏长度是2cm,这只牙膏最多能用多少天?(得数保留整数)
练习七
5mm=0.5cm
3.14×(0.5÷2) ×2×2=0.785(立方厘米)=0.785(毫升)
120÷0.785≈152(天)
答:这只牙膏最多能用152天。
2
6、一个圆柱形木桶(如图,木桶平置),底面内直径为4dm,桶口距底面最小的高度为5dm,最大高度为7dm。该桶最多能装多少升水?
练习七
分析:桶口距底面最小高度为5dm,即桶中水的最大高度为5cm。
3.14×(4÷2) ×5=62.8(立方分米)=62.8(升)
答:该桶最多能装62.8升水。
2
1、判断:
基础练习
(1)长方体、正方体、圆柱体的体积都可以用底面积
乘以高来计算。( ? ? ? )
(2)圆锥的体积是圆柱体积的? ? ?。( ? ? ? )
(3)一个圆柱形杯子的体积等于它的容积。( ? ? ? )
2、回答下面的问题,并列出算式:
一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
基础练习
2×3.14×10=62.8(分米)
3.14×10 ?=314(平方分米)
2
3.14×10 ?+2×3.14×10×20=1570(平方分米)
2
3.14×10 ?×20=6280(立方分米)
2
3.填空
(1)一个圆柱体水桶的容积是50立方分米,内底面积是10平方分米,水桶深( ? ? ? ? ?)分米。?
(2)一个圆锥体零件的体积是30立方厘米,底面积是15平方厘米,它的高是( ? ? ? ? ?)厘米。?
(3)一根圆柱形木材长20分米,把截成4个相等的圆柱体. 表面积增加了18.84平方分米.底面的面积是( ? ? ? ? )平方分米。
基础练习
5
6
3.14
1.选择正确答案。
(1)把一个圆柱体的木块切削成一个最大的圆锥,削去部分的体积是圆柱的(? ? ? ? ? )。?
A.? ? ? ? ? ? ? ? ? ? ? ? ? ? ?B .? ? ? ? ? ? ? ? ? ? ? ? C . 3倍?
(2)把一根圆柱体木料锯成三段,增加了( )个底面积。
A . 2? ? ? ? ? ? ? ? ? ? ? ? B . 3? ? ? ? ? ? ? ? ? ? ?C . 4?
(3)圆柱的底面半径缩小? ? ?, 高扩大2倍,它的体积(? ? ? ? ?)。?
A . 扩大2倍? ? ? ? ? ?B .缩小? ? ? ? ? ? ? ? ?C . 不变
提高练习
B
B
C
(4)用一块边长31.4分米的正方形铁皮,配上半径是( ? ? ? ? ? )分米的圆形底面就能做成一个圆柱体容器。
提高练习
A . 10? ? ? ? ? ? ? ? ? ? ? ? ? ?B. 4.71 ? ? ? ? ? ? ? ? ? ? ? ? ? ?C . 5
(5)在一个半径为r的圆柱体容器内,完全浸入一个圆锥,水面上升h,这个圆锥的体积是( )。
(6)把一个底面积是2.4平方分米,高3分米的圆锥形铁器放在一个装满水的圆柱形容器中,容器中会有(? ? ? ? )立方分米的水溢出。
A. 7.2 立方分米? ? ? ? ? B. 2.4立方分米 ? ? ? ? ? ? ? C.没法计算
C
A
B
2.填空?
(1)一个圆锥体的玻璃杯高9厘米,盛满水后倒入与它等底等高的圆柱体玻璃杯中,这时水深( ? ? ? ? ?)厘米。?
(2)一个圆柱和一个圆锥等底等高,它们的体积之和是32立方分米,圆锥的体积是( ? ? ? ? ? )立方分米。?
(3)在正方体中截取最大圆柱体,圆柱的体积是正方体体积的( ? ? ? ? )%。
提高练习
3
8
78.5
3. 选择合适的图片制作圆柱圆锥。
提高练习
d=4cm
弧长=12cm
d=1cm
弧长=3.14cm
(1)
(2)
(3)
(4)
4cm
12.56cm
(5)
d=5cm
d=4cm
(1)(5)(6) ? ? ? 制作成圆柱
(3)(4)
制作成圆锥
想一想还有其他的选择吗?
(6)
(8)
(7)
2cm
8.84cm
提高练习
4、一个圆锥形的沙堆,底面周长是31.4m,高是7.2m,每立方米沙重1.5吨,如果用一辆载重6吨的汽车来运,几次可以运完?
解:底面半径:31.4÷3.14÷2=5(m)
沙堆的体积:? ?× 3.14 × 5 × 7.2=188.4(m? )
188.4 × 1.5÷6≈48(次)
答:48次可以运完。
2
3
1.甲乙两人分别利用一张长10厘米,宽5厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( ? ? )。
A、高一定相等
B、侧面积一定相等
C、侧面积和高都相等
D、侧面积和高都不相等
拓展练习
B
2.圆锥的侧面积展开图是一个扇形,这个扇形的圆心角n范围是( ? ? ?). ? ? ? ??
拓展练习
C
3.一根圆柱形木材长20分米,把它截成4个相等的圆柱体.表面积增加了18.84平方分米.截后每段圆柱体积是( ? ? ? ? ? ? ?)立方分米.
15.7
拓展练习
4.一个圆柱的侧面积是12.56平方厘米,底面半径是2厘米,那么这个圆柱的体积是( ? ? ? ? ? ? ? ? )立方厘米.
拓展练习
12.56
注意:圆柱体的体积可以这样算:侧面积乘以半径÷2
5.已知两个体积不同的圆柱,高相等,它们的底面半径的比是1:2,那么它们的体积的比是( ? ? ? ? ? ?)
拓展练习
1:4
圆柱体1
圆柱体2
1? ? ? ? ? ? ? ? ? ? ? ?2
1? ? ? ? ? ? ? ? ? ? ? ?4
1? ? ? ? ? ? ? ? ? ? ? ?1
1? ? ? ? ? ? ? ? ? ? ? ?4
半径
底面积
高
体 积
6、一个圆柱与一个圆锥的底面积和体积相等,那么圆锥的高是圆柱高的( ? ? ? ? ?).
拓展练习
3倍
7、把一个横截面为正方形的长方体,削成一个最大的圆锥体,已知圆锥体的底面周长6.28厘米,高5厘米,长方体的体积是
( ? ? ? ? ? )立方厘米
拓展练习
正方形边长:6.28÷3.14=2(厘米)
长方体体积:2×2×5=20(立方厘米)
20
8、一个圆柱体水桶,底面半径为20厘米,里面盛有80厘米深的水,现将一个底面周长为62.8厘米的圆锥体铁块完全沉入水桶里,水比原来上升了b。问圆锥体铁块的高是多少厘米?
拓展练习
解:分析题可知,上升的水的体积等于铁块体积。
上升的水的高度为: 80xd=5(cm)
铁块的体积V=3.14x20 ?x5=6280(cm ?)
铁块的底面积为:3.14x(62.8÷3.14÷2) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? =314(cm ?)
铁块的高为:6280 x3÷314= 60(cm)
答:圆锥体铁块的高是60厘米。
2
2
2
3
2
9、一个圆柱体,已知高度每增加1厘米,它的侧面积就增加31.4平方厘米,如果高是16厘米,则它的体积是多少立方厘米?
拓展练习
解:依题意可知,
圆柱体的底面周长=31.4÷1=31.4(cm)
圆柱体的底面半径=31.4÷3.14÷2=5(cm)
圆柱体的底面积=3.14×5?=78.5(cm ?)
圆柱体的体积=78.5 ×16=1256(cm ?) ?
答:它的体积是1256立方厘米。
3
祖暅原理
祖冲之
祖暅
祖暅原理
祖暅简介
? ? 祖暅,字景烁,祖冲之之子,范阳郡蓟县人(今河北省涞源
县人),南北朝时代的伟大科学家。祖暅在数学上有突出贡献,他在实践的基础上,于5世纪末提出了体积的计算原理。祖暅原理:“幂势既同,则积不容异”。
“势”即是高,“幂”即是面积。
祖暅原理
祖暅原理“幂势既同,则积不容异”
祖暅原理
? ? 夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
祖冲之父子是我们中华民族的骄傲和自豪。
? ? 祖暅原理的提出要比其他国家的数学家早一千多年。在欧洲直到17世纪,才有意大利数学家卡瓦列里提出上述结论。
祖暅原理
祖暅原理“幂势既同,则积不容异”
祖暅原理
? ? 设有底面积都等于S,高都等于h的任意一个棱柱、一个圆柱和一个长方体,使它们的下底面在同一平面内。你能得到什么结论?
祖暅原理与柱体的体积
祖暅原理
祖暅原理与柱体的体积
祖暅原理
由祖暅原理可得:
V柱体=Sh 其中S 是柱体的底面积,
h是柱体的高。
祖暅原理
祖暅原理与柱体的体积
祖暅原理与柱体的体积
设有底面积都等于S,高都等于h的两个锥体(如图:一个棱锥和一个圆锥),使它们的下底面在同一平面内。你能得到什么结论?
祖暅原理
等底面积等高的两个锥体的体积相等
? ? ? ? 结论:对于一个任意的锥体,设它的底面积为S,高为h,那么它的体积应等于一个底面积为S,高为h的三棱锥的体积。即
祖暅原理
祖暅原理与柱体的体积
如何截最大的圆柱与圆锥
如何截最大的圆柱与圆锥
(1)在正方体中截取最大圆柱体:
方法:1
这个圆柱体与正方体的高相等,所以体积的比就是底面积的比。而底面积之间的关系就是圆与外切正方形之间的面积关系,即 ? ? ?:4。因此这个圆柱体的体积就是正方体体积的
方法:2
设:正方体的棱长为10厘米。
10厘米
如何截最大的圆柱与圆锥
785÷1000=78.5%
如何截最大的圆柱与圆锥
方法:3
设圆柱底面半径为x厘米。
(2)在底面为正方形的长方体中截取最大圆柱体。
如何截最大的圆柱与圆锥
方法1
设长方体的棱长分别为10、10、12厘米。
以正方形这个面作为圆柱体的底面去截圆柱体,体积为:
以长方形面作为圆柱体的底面去截圆柱体,体积为:
×3.14×12=942(立方厘米)
×3.14×10=785(立方厘米)
方法2
根据浪费材料的多少,发现以正方形为底面去截圆柱体浪费的材料最少。而这样截取圆柱体,这个圆柱体与长方体的高相等,所以体积的比就是底面积的比。而底面积之间的关系就是圆与外切正方形之间的面积关系,即 ? ? :4。因此这个圆柱体的体积就是长方体体积的
如何截最大的圆柱与圆锥
(3)长、宽、高均不相等的长方体。
如何截最大的圆柱与圆锥
方法1:逐个面去求。
1、以6×4这个面去截,圆柱体体积为:
2、以2×4这个面去截,圆柱体体积为:
3、以6×2这个面去截,圆柱体体积为:
×3.14×2=25.12(立方厘米)
如何截最大的圆柱与圆锥
方法2:转化为底面为正方形的长方体。
虽然也是按三个面去思考,但是并不用求出每个圆柱体的体积。因为:
以10×6这个面去截,圆柱体体积就是 6×6×4的长方体体积的78.5%。
以4×6这个面去截,圆柱体体积就是4×4×10的长方体体积的78.5%。
以10×4这个面去截,圆柱体体积就是4×4×6的长方体体积的78.5%。
因此只要比较这3个长方体体积就可以知道哪个圆柱体的体积最大了。
6厘米
10厘米
4厘米
如何截最大的圆柱与圆锥
方法3:
1、以a×b为底面去削圆柱:
2、以b×c为底面去削圆柱:
3、以a×c为底面去削圆柱:
显然2>3,只要比较1和2就可以了
体积为:
体积为:
体积为:
a >b >c >0
1、以a×b为底面去削圆柱:
2、以b×c为底面去削圆柱:
体积为:
体积为:
如何截最大的圆柱与圆锥
a >b >c
:
V1 ? ??V2=
:
下面我们从三种情况来分析来:
如何截最大的圆柱与圆锥
(1) ? ? ? ? ? ? ?,以a×b为底面去削圆柱体积最大,如棱长分别为1,2,3时。
(2) ? ? ? ? ? ? ?,以b×c为底面去削圆柱体积最大,如棱长分别为1,2,5时。
(3) ? ? ? ? ? ? ?,以a×b,b×c为底面去削圆柱体都可以,如棱长分别为1,2,4时。
1
1
如何截最大的圆柱与圆锥
思考:把一个棱长为a的正方体木块削成体积最大的圆锥体,
这个圆锥体的体积是多少?
不是最大
通过整理复习,进一步巩固认识圆柱和圆锥的特征以及他们之间的联系。
熟练掌握圆柱表面积、体积和圆锥体积的计算方法。
进一步发展空间观念,提高解决实际问题的能力。
教学目标
圆柱、圆锥表面积、体积的计算。
圆柱、圆锥的特征和它们的体积之间的联系与区别。
教学重点
教学难点
圆 锥
圆锥的认识
圆锥体积的计算
圆 柱
圆柱的体积
底面积
圆柱的表面积
圆柱的侧面积
圆柱的特征
圆柱各部分的名称
圆柱?
?和?
圆锥
1、圆柱与圆锥各有哪些特征?
2、怎样求圆柱的侧面积.表面积.体积?
计算公式各是什么?
3、怎样求圆锥的体积?计算公式是什么?
4、圆柱与圆锥的体积之间有什么系?
1、圆柱与圆锥各有哪些特征?
2、怎样求圆柱的侧面积.表面积.体积?计算公式各是什么?
3、怎样求圆锥的体积?计算公式是什么?
4、圆柱与圆锥的体积之间有什么系?
圆
柱?
和?
圆?
锥
圆柱的认识
圆柱的表面积
圆柱的体积
圆锥的认识
圆锥的体积
组成:
特征:
两个底面、一个侧面。
底面是完全相同的两个圆;侧面是曲面,展开是一个长方形(或正方形);圆柱有无数条高。
S侧=ch=2πrh=πdh
S=S侧+2S底
组成:
特征:底面是一个圆;侧面是曲面,展开是一个扇形;圆锥只有一条高。
一个底面,一个侧面。
知识整理
知识整理
类别
特 征
表面积
体 积
关 系
形 成
圆
柱
圆
锥
1个侧面(曲面)2个底面(圆形)无数条高上下粗细一样
1个顶点
1个侧面(曲面)
1个底面(圆形)?
1条高
体积是等底
等高的圆锥
体积的3倍
体积是等底等高的圆柱
体积的
V=sh
S=
圆柱的特征:
知识整理
1.两个底面是半径相等的两个圆
2.圆柱有一个曲面叫做侧面,沿高展开后是
一个长方形(或正方形)。
3.圆柱有无数条高,且高的长度都相等
长=底面周长
宽=高
圆柱的表面积怎样计算呢?
知识整理
圆柱的侧面积=底面周长×高
底面
底面
侧面
底面周长=长
高=宽
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
高等于圆柱的 高 。
长方体的底面积等于圆柱的 底面积 ,
长方体体积=底面积×高
圆柱体积
=底面积×高
V=Sh
||
知识整理
圆锥的特征:
知识整理
1.圆锥的底面是一个圆
2.圆锥的侧面是一个曲面,
展开后是一个扇形
3.圆锥只有一个顶点,一条高。
(从顶点到底面圆心的距离是圆锥的高)
圆柱侧面积=底面周长×高
圆柱表面积=侧面积+底面积×2
圆 柱 体积=底面积×高
圆 锥 体积=底面积×高÷3
基
本
公
式
知识整理
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的三分之一
等底等高圆柱体积是圆锥体积的3倍
知识整理
等底等高的圆柱和圆锥体积有以下关系:
柱锥关系
规律:等底等高的圆柱和圆锥体积:锥1、差2、柱3、和4
(1)圆锥体积是圆柱的
(2)圆柱体积是圆锥的3倍
(3)圆锥体积比圆柱少
(4)圆柱体积比圆锥多2倍
等底等高
柱锥关系
V柱=
3V锥
你知道圆柱和圆锥是啥关系吗?
V柱=45立方厘米 V锥=?立方厘米
V柱= ? ? ? 立方厘米 ? ? ? ?V锥=24立方厘米
柱锥关系
S? ? ? ? ? ? ? ? =? ? ? ? ? ? ? ? ?S
?
72
圆柱与圆锥的关系
1、圆柱与圆锥的体积,底面积相等,则圆柱的高是圆锥高得 ? ? ?,圆锥的高是圆柱高的3倍。
2、圆柱与圆锥的体积,高相等,则圆柱的底面积是圆锥底面积得 ? ? ?,圆锥的底面积是圆柱底面积的3倍。
柱锥关系
等积等底
柱锥关系
h柱=18分米 ? ? ? ? ? ? ? ? ?h锥= ? ? 分米
54
?
你知道圆柱和圆锥是啥关系吗?
h柱= ? ? ?分米 ? ? ? ? ?h锥=42分米
柱锥关系
14
?
等积等高
S柱=18平方分米 ? ? ? ? ?S锥= ? ? ?平方分米
你知道圆柱和圆锥是啥关系吗?
柱锥关系
V ? ? ? ? ? ? ? ? ?= ? ? ? ? ? ? ? ? V
54
?
V? ? ? ? ? ? ? ? ?= ? ? ? ? ? ? ? ? V
S柱= ? ? ?平方分米 ? ? ? ? ? ?S锥=27平方分米
9
?
柱锥关系
1.将下面图形分类。说说每类图形的名称和特征。
整理与复习
图1
图2
图3
图4
图5
图6
圆柱
圆锥
圆柱:图中第1、2、6、幅图是圆柱。其特征是圆柱的两个底面都是圆,并且大小相同;圆柱的侧面是曲面,侧面沿高展开后是一个长方形(或正方形);圆柱有无数条高,长度都相等。
圆锥:第3、4、5幅图是圆锥。其特征是圆锥的底面是一个圆;侧面是一个曲面,侧面展开后是一个扇形;圆锥只有一条高(顶点到底面圆心的距离)。
整理与复习
2.想一想 圆柱的侧面积、表面积怎样计算?圆锥的体积公式是怎样导出的?在填写下表。
整理与复习
圆柱的侧面积=底面周长×高圆柱的表面积=圆柱的侧面积+两个底面积圆柱的体积公式是把它转化成长方体而推导出来的;
圆锥的体积是通过装水和沙试验推导出来的。
圆柱表面积用字母表示为:
S表= S侧+2S底
圆柱侧面积用字母表示为:
整理与复习
直接计算:S侧=Ch
利用直径计算:
利用半径计算:
运用圆柱的表面积公式解决实际问题时,并不是所有的圆柱形物体都有两个底面,有的没有底面,要根据实际情况选择合理的解题方法。
圆柱体积用字母表示为:
圆锥体积用字母表示为:
整理与复习
无论是求圆柱的表面积还是体积,如果给底面直径或周长要先求出半径。侧面积可以直接用公式求。
求圆锥的体积不要忘记乘
整理与复习
名称
半径
直径
高
表面积
体积
圆柱
圆锥
5dm
1m
20cm
2dm
0.5m
10dm
2m
40cm
4dm
1m
4dm
0.7m
5cm
2.4dm
4.5m
3.妈妈给小雨的塑料壶做了一个布套(如图)小雨每天上学带一壶水。
(1)至少用了多少布料?
(2)小雨在学校一天喝1.5L的水,这壶水够喝吗?(水壶的厚度忽略不计。)
整理与复习
分析:求所用布料就是求水壶的表面积,求能装多少水即求水壶的体积。
(1)3.14×10×20+2×3.14 ×(10÷2)
整理与复习
答:布料使用面积为
(2) 3.14×(10÷2)
1.57L>1.5L
答:这壶水够喝。
4.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。底面直径是4dm,圆柱高2dm,圆锥高4dm, 每立方分米稻谷重0.65kg。
(1)这个漏斗最多能装多少千克稻谷?
(2)如果稻谷的出米率是70%,一漏斗能磨多少大米?
整理与复习
答:这个漏斗最多能装? ? ? ? ? 千克稻谷。
答:一漏斗稻谷能磨? ? ? ? ? ? ?千克大米。
整理与复习
分析:漏斗是由一个圆柱和一个圆锥组合而成的。
1、把一块长方体钢坯铸造成一根直径为4dm的圆柱形钢筋,求钢筋的长度。
练习七
分析:等积变形题。长方体的体积和圆柱的体积相等,钢筋的长度(圆柱的高)等于求出长方体的体积除以圆柱的底面积。
长方体的体积(圆柱的体积):12.56×5×4=251.2(立方分米)
圆柱的底面积: 3.14 ×(4÷2)
钢筋的长度:251.2÷12.56=20(分米)
答:钢筋的长度是20分米。
2. 一个圆锥形沙堆,底面积是28.26m ?,高是2.5m。用这堆 沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
2
练习七
分析:首先要明确公路的形状是一个近似的长方体,圆锥形
沙堆的体积等于长方体的体积。还要注意单位换算。
2cm=0.02m
(长=长方体的体积÷宽÷高)
沙堆的体积:?
所铺公路的长度:
23.55÷10÷0.02=2.355÷0.02
=117.75(米)
答:能铺117.75米。
=9.42×2.5
=23.55(立方米)
3、一块蜂窝煤如图所示。做一块蜂窝煤大约需要煤多少立方分米?
练习七
分析:蜂窝煤的体积等于大圆柱的体积减去12个中空的小圆柱的体积。
3.14×(12÷2) ×9- 3.14×(2÷2) ×9×12
=1017.36-339.12
=678.24(立方厘米)
=0.67824(立方分米)
答:做一块蜂窝煤大约需要煤0.67824立方分米。
2
2
4、有块正方体的木料,它的棱长是4dm。把这块木料加工成一个最大的圆柱体(如图)。这个圆柱的体积是多少?
练习七
3.14×(4÷2) ×4=50.24(立方分米)
答:这个圆柱体的体积是50.24立方分米。
2
5、一支120ml的牙膏管口的直径为5mm,李叔叔每天刷牙2次,每次挤出的牙膏长度是2cm,这只牙膏最多能用多少天?(得数保留整数)
练习七
5mm=0.5cm
3.14×(0.5÷2) ×2×2=0.785(立方厘米)=0.785(毫升)
120÷0.785≈152(天)
答:这只牙膏最多能用152天。
2
6、一个圆柱形木桶(如图,木桶平置),底面内直径为4dm,桶口距底面最小的高度为5dm,最大高度为7dm。该桶最多能装多少升水?
练习七
分析:桶口距底面最小高度为5dm,即桶中水的最大高度为5cm。
3.14×(4÷2) ×5=62.8(立方分米)=62.8(升)
答:该桶最多能装62.8升水。
2
1、判断:
基础练习
(1)长方体、正方体、圆柱体的体积都可以用底面积
乘以高来计算。( ? ? ? )
(2)圆锥的体积是圆柱体积的? ? ?。( ? ? ? )
(3)一个圆柱形杯子的体积等于它的容积。( ? ? ? )
2、回答下面的问题,并列出算式:
一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
基础练习
2×3.14×10=62.8(分米)
3.14×10 ?=314(平方分米)
2
3.14×10 ?+2×3.14×10×20=1570(平方分米)
2
3.14×10 ?×20=6280(立方分米)
2
3.填空
(1)一个圆柱体水桶的容积是50立方分米,内底面积是10平方分米,水桶深( ? ? ? ? ?)分米。?
(2)一个圆锥体零件的体积是30立方厘米,底面积是15平方厘米,它的高是( ? ? ? ? ?)厘米。?
(3)一根圆柱形木材长20分米,把截成4个相等的圆柱体. 表面积增加了18.84平方分米.底面的面积是( ? ? ? ? )平方分米。
基础练习
5
6
3.14
1.选择正确答案。
(1)把一个圆柱体的木块切削成一个最大的圆锥,削去部分的体积是圆柱的(? ? ? ? ? )。?
A.? ? ? ? ? ? ? ? ? ? ? ? ? ? ?B .? ? ? ? ? ? ? ? ? ? ? ? C . 3倍?
(2)把一根圆柱体木料锯成三段,增加了( )个底面积。
A . 2? ? ? ? ? ? ? ? ? ? ? ? B . 3? ? ? ? ? ? ? ? ? ? ?C . 4?
(3)圆柱的底面半径缩小? ? ?, 高扩大2倍,它的体积(? ? ? ? ?)。?
A . 扩大2倍? ? ? ? ? ?B .缩小? ? ? ? ? ? ? ? ?C . 不变
提高练习
B
B
C
(4)用一块边长31.4分米的正方形铁皮,配上半径是( ? ? ? ? ? )分米的圆形底面就能做成一个圆柱体容器。
提高练习
A . 10? ? ? ? ? ? ? ? ? ? ? ? ? ?B. 4.71 ? ? ? ? ? ? ? ? ? ? ? ? ? ?C . 5
(5)在一个半径为r的圆柱体容器内,完全浸入一个圆锥,水面上升h,这个圆锥的体积是( )。
(6)把一个底面积是2.4平方分米,高3分米的圆锥形铁器放在一个装满水的圆柱形容器中,容器中会有(? ? ? ? )立方分米的水溢出。
A. 7.2 立方分米? ? ? ? ? B. 2.4立方分米 ? ? ? ? ? ? ? C.没法计算
C
A
B
2.填空?
(1)一个圆锥体的玻璃杯高9厘米,盛满水后倒入与它等底等高的圆柱体玻璃杯中,这时水深( ? ? ? ? ?)厘米。?
(2)一个圆柱和一个圆锥等底等高,它们的体积之和是32立方分米,圆锥的体积是( ? ? ? ? ? )立方分米。?
(3)在正方体中截取最大圆柱体,圆柱的体积是正方体体积的( ? ? ? ? )%。
提高练习
3
8
78.5
3. 选择合适的图片制作圆柱圆锥。
提高练习
d=4cm
弧长=12cm
d=1cm
弧长=3.14cm
(1)
(2)
(3)
(4)
4cm
12.56cm
(5)
d=5cm
d=4cm
(1)(5)(6) ? ? ? 制作成圆柱
(3)(4)
制作成圆锥
想一想还有其他的选择吗?
(6)
(8)
(7)
2cm
8.84cm
提高练习
4、一个圆锥形的沙堆,底面周长是31.4m,高是7.2m,每立方米沙重1.5吨,如果用一辆载重6吨的汽车来运,几次可以运完?
解:底面半径:31.4÷3.14÷2=5(m)
沙堆的体积:? ?× 3.14 × 5 × 7.2=188.4(m? )
188.4 × 1.5÷6≈48(次)
答:48次可以运完。
2
3
1.甲乙两人分别利用一张长10厘米,宽5厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( ? ? )。
A、高一定相等
B、侧面积一定相等
C、侧面积和高都相等
D、侧面积和高都不相等
拓展练习
B
2.圆锥的侧面积展开图是一个扇形,这个扇形的圆心角n范围是( ? ? ?). ? ? ? ??
拓展练习
C
3.一根圆柱形木材长20分米,把它截成4个相等的圆柱体.表面积增加了18.84平方分米.截后每段圆柱体积是( ? ? ? ? ? ? ?)立方分米.
15.7
拓展练习
4.一个圆柱的侧面积是12.56平方厘米,底面半径是2厘米,那么这个圆柱的体积是( ? ? ? ? ? ? ? ? )立方厘米.
拓展练习
12.56
注意:圆柱体的体积可以这样算:侧面积乘以半径÷2
5.已知两个体积不同的圆柱,高相等,它们的底面半径的比是1:2,那么它们的体积的比是( ? ? ? ? ? ?)
拓展练习
1:4
圆柱体1
圆柱体2
1? ? ? ? ? ? ? ? ? ? ? ?2
1? ? ? ? ? ? ? ? ? ? ? ?4
1? ? ? ? ? ? ? ? ? ? ? ?1
1? ? ? ? ? ? ? ? ? ? ? ?4
半径
底面积
高
体 积
6、一个圆柱与一个圆锥的底面积和体积相等,那么圆锥的高是圆柱高的( ? ? ? ? ?).
拓展练习
3倍
7、把一个横截面为正方形的长方体,削成一个最大的圆锥体,已知圆锥体的底面周长6.28厘米,高5厘米,长方体的体积是
( ? ? ? ? ? )立方厘米
拓展练习
正方形边长:6.28÷3.14=2(厘米)
长方体体积:2×2×5=20(立方厘米)
20
8、一个圆柱体水桶,底面半径为20厘米,里面盛有80厘米深的水,现将一个底面周长为62.8厘米的圆锥体铁块完全沉入水桶里,水比原来上升了b。问圆锥体铁块的高是多少厘米?
拓展练习
解:分析题可知,上升的水的体积等于铁块体积。
上升的水的高度为: 80xd=5(cm)
铁块的体积V=3.14x20 ?x5=6280(cm ?)
铁块的底面积为:3.14x(62.8÷3.14÷2) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? =314(cm ?)
铁块的高为:6280 x3÷314= 60(cm)
答:圆锥体铁块的高是60厘米。
2
2
2
3
2
9、一个圆柱体,已知高度每增加1厘米,它的侧面积就增加31.4平方厘米,如果高是16厘米,则它的体积是多少立方厘米?
拓展练习
解:依题意可知,
圆柱体的底面周长=31.4÷1=31.4(cm)
圆柱体的底面半径=31.4÷3.14÷2=5(cm)
圆柱体的底面积=3.14×5?=78.5(cm ?)
圆柱体的体积=78.5 ×16=1256(cm ?) ?
答:它的体积是1256立方厘米。
3
祖暅原理
祖冲之
祖暅
祖暅原理
祖暅简介
? ? 祖暅,字景烁,祖冲之之子,范阳郡蓟县人(今河北省涞源
县人),南北朝时代的伟大科学家。祖暅在数学上有突出贡献,他在实践的基础上,于5世纪末提出了体积的计算原理。祖暅原理:“幂势既同,则积不容异”。
“势”即是高,“幂”即是面积。
祖暅原理
祖暅原理“幂势既同,则积不容异”
祖暅原理
? ? 夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。
祖冲之父子是我们中华民族的骄傲和自豪。
? ? 祖暅原理的提出要比其他国家的数学家早一千多年。在欧洲直到17世纪,才有意大利数学家卡瓦列里提出上述结论。
祖暅原理
祖暅原理“幂势既同,则积不容异”
祖暅原理
? ? 设有底面积都等于S,高都等于h的任意一个棱柱、一个圆柱和一个长方体,使它们的下底面在同一平面内。你能得到什么结论?
祖暅原理与柱体的体积
祖暅原理
祖暅原理与柱体的体积
祖暅原理
由祖暅原理可得:
V柱体=Sh 其中S 是柱体的底面积,
h是柱体的高。
祖暅原理
祖暅原理与柱体的体积
祖暅原理与柱体的体积
设有底面积都等于S,高都等于h的两个锥体(如图:一个棱锥和一个圆锥),使它们的下底面在同一平面内。你能得到什么结论?
祖暅原理
等底面积等高的两个锥体的体积相等
? ? ? ? 结论:对于一个任意的锥体,设它的底面积为S,高为h,那么它的体积应等于一个底面积为S,高为h的三棱锥的体积。即
祖暅原理
祖暅原理与柱体的体积
如何截最大的圆柱与圆锥
如何截最大的圆柱与圆锥
(1)在正方体中截取最大圆柱体:
方法:1
这个圆柱体与正方体的高相等,所以体积的比就是底面积的比。而底面积之间的关系就是圆与外切正方形之间的面积关系,即 ? ? ?:4。因此这个圆柱体的体积就是正方体体积的
方法:2
设:正方体的棱长为10厘米。
10厘米
如何截最大的圆柱与圆锥
785÷1000=78.5%
如何截最大的圆柱与圆锥
方法:3
设圆柱底面半径为x厘米。
(2)在底面为正方形的长方体中截取最大圆柱体。
如何截最大的圆柱与圆锥
方法1
设长方体的棱长分别为10、10、12厘米。
以正方形这个面作为圆柱体的底面去截圆柱体,体积为:
以长方形面作为圆柱体的底面去截圆柱体,体积为:
×3.14×12=942(立方厘米)
×3.14×10=785(立方厘米)
方法2
根据浪费材料的多少,发现以正方形为底面去截圆柱体浪费的材料最少。而这样截取圆柱体,这个圆柱体与长方体的高相等,所以体积的比就是底面积的比。而底面积之间的关系就是圆与外切正方形之间的面积关系,即 ? ? :4。因此这个圆柱体的体积就是长方体体积的
如何截最大的圆柱与圆锥
(3)长、宽、高均不相等的长方体。
如何截最大的圆柱与圆锥
方法1:逐个面去求。
1、以6×4这个面去截,圆柱体体积为:
2、以2×4这个面去截,圆柱体体积为:
3、以6×2这个面去截,圆柱体体积为:
×3.14×2=25.12(立方厘米)
如何截最大的圆柱与圆锥
方法2:转化为底面为正方形的长方体。
虽然也是按三个面去思考,但是并不用求出每个圆柱体的体积。因为:
以10×6这个面去截,圆柱体体积就是 6×6×4的长方体体积的78.5%。
以4×6这个面去截,圆柱体体积就是4×4×10的长方体体积的78.5%。
以10×4这个面去截,圆柱体体积就是4×4×6的长方体体积的78.5%。
因此只要比较这3个长方体体积就可以知道哪个圆柱体的体积最大了。
6厘米
10厘米
4厘米
如何截最大的圆柱与圆锥
方法3:
1、以a×b为底面去削圆柱:
2、以b×c为底面去削圆柱:
3、以a×c为底面去削圆柱:
显然2>3,只要比较1和2就可以了
体积为:
体积为:
体积为:
a >b >c >0
1、以a×b为底面去削圆柱:
2、以b×c为底面去削圆柱:
体积为:
体积为:
如何截最大的圆柱与圆锥
a >b >c
:
V1 ? ??V2=
:
下面我们从三种情况来分析来:
如何截最大的圆柱与圆锥
(1) ? ? ? ? ? ? ?,以a×b为底面去削圆柱体积最大,如棱长分别为1,2,3时。
(2) ? ? ? ? ? ? ?,以b×c为底面去削圆柱体积最大,如棱长分别为1,2,5时。
(3) ? ? ? ? ? ? ?,以a×b,b×c为底面去削圆柱体都可以,如棱长分别为1,2,4时。
1
1
如何截最大的圆柱与圆锥
思考:把一个棱长为a的正方体木块削成体积最大的圆锥体,
这个圆锥体的体积是多少?
不是最大
