六年级上册数学课件-圆的面积 人教版(共52ppt)
文档属性
| 名称 | 六年级上册数学课件-圆的面积 人教版(共52ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 00:00:00 | ||
图片预览








文档简介
圆的面积
教学目标
使学生理解圆面积计算公式的推导过程,掌握圆面积计算公式。
使学生能利用圆面积的计算公式正确进行圆面积计算,并能解决有关圆面积的实际问题。
使学生理解圆环的形成,并能正确计算圆环面积。
教学重点
教学难点
圆面积的计算公式的推导。
理解圆的周长和半径与转化后近似长方形的长和宽的关系。
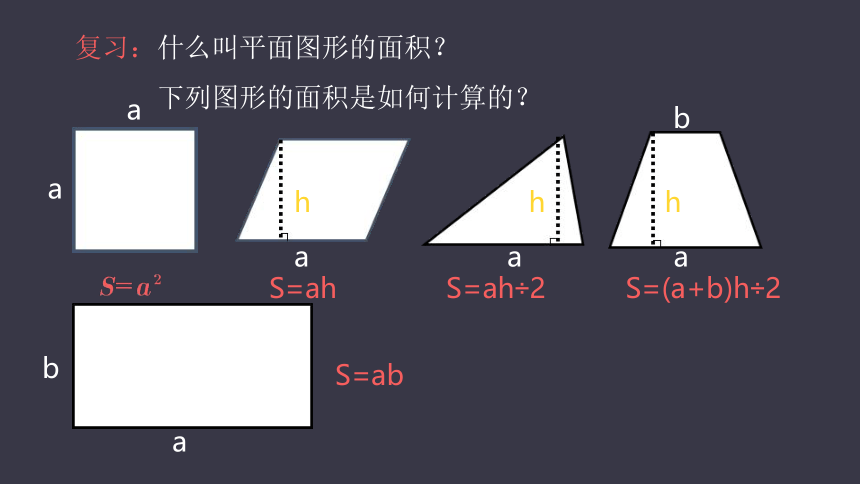
复习:什么叫平面图形的面积?
下列图形的面积是如何计算的?
a
a
a
a
a
a
b
h
h
h
b
S=ah
S=ah÷2
S=(a+b)h÷2
S=ab
圆所占平面的大小叫做圆的面积。
怎样计算一个圆的面积呢?
能不能和学过的图形联系起来呢?如果知道了圆的半径,可以计算出图中圆内外的两个正方形的面积,圆的面积介于这两个正方形面积之间。
如何得到一个圆的面积?想一想,并与同伴交流。
如何得到一个圆的面积?想一想,并与同伴交流。
如何得到一个圆的面积?想一想,并与同伴交流。
圆的面积是正方形面积(半径的平方)的3倍多一些。
r
o
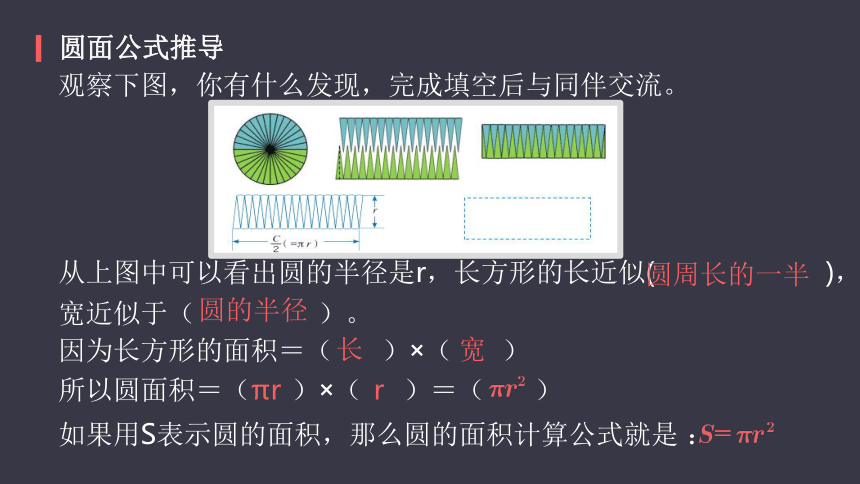
圆面公式推导
观察下图,你有什么发现,完成填空后与同伴交流。
从上图中可以看出圆的半径是r,长方形的长近似(? ? ? ? ? ? ? ? ? ? ?),宽近似于(? ? ? ? ? ? ? ?)。
因为长方形的面积=(? ? ? )×(? ? ? )
所以圆面积=(? ? ?)×(? ? ?)=(? ? ? )
如果用S表示圆的面积,那么圆的面积计算公式就是 :
圆周长的一半
圆的半径
长
宽
πr
r
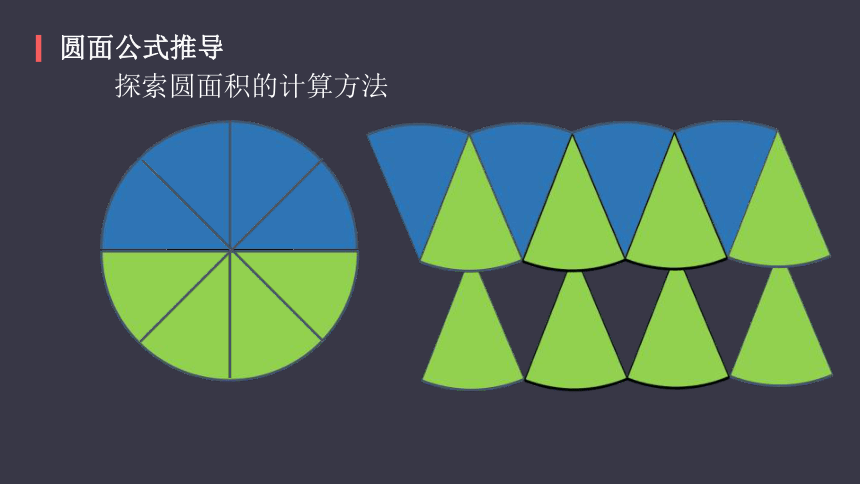
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆的面积
平行四边形的面积
平行四边形的面积=底×高
圆周长的一半
圆的面积
圆的半径
C÷2
底
r
高
×
πr
×
r
S=
圆面公式推导
探索圆面积的计算方法
C÷2
r
长
宽
圆的面积
长方形的面积
长方形的面积=底×高
圆周长的一半
圆的半径
×
πr
×
r
S=
圆的面积
例1
圆形草坪的直径是20 m,每平方米草皮8 元,铺满草坪需要多少钱?
从题目中你都知道了什么?
要求铺满草坪需要多少钱,先要求出圆形草坪的面积是多少平方米。
20÷2=10(m)
314×8=2512(元)
答:铺满草皮需要2512 元。
3.14×10?=314(m?)
做一做
一个圆形茶几桌面的直径是1 m,它的面积是多少平方米?
先求出半径,再求圆的面积。
1÷2=0.5(m)
3.14×0.5?=0.785(m?)
答:它的面积是0.785 m?。
圆环面积导入
求下面各圆的面积。(口头列式)
3.14×1 =3.14(平方厘米)
3.14×(4÷2) =12.56 (平方厘米)
2
2
圆环面积导入
仔细观察这些图案,你有什么发现?
例2
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
怎样利用内圆和外圆的面积求出圆环的面积?
3.14×6?-3.14×2?
=113.04-12.56
=100.48(cm?)
3.14×(6?-2?)
=3.14×32
=100.48(cm?)
还可以这样计算……
我是这样想的……
答:圆环的面积是100.48 cm?。
做一做
一个圆形环岛的直径是50 m,中间是一个直径为10 m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
要求草坪的占地面积,也就是求圆环的面积。
50÷2=25(m)? ? ? ? 10÷2=5(m)
3.14×(25?-5?)
=3.14×600
=1884(m?)
答:草坪的占地面积是1884 m?。
练习
完成下表。
4cm
50.24cm?
9cm
6cm
20cm
8cm
63.585cm?
28.26cm?
1256cm?
40cm
4.5cm
3cm
半径
直径
圆面积
练习
计算下面各圆的周长和面积。
左图:3.14×10=31.4(cm)
3.14×(10÷2)?=78.5(cm?)
右图:3.14×3×2=18.84(cm)
3.14×3?=28.26(cm?)
练习
公园草地上一个自动旋转喷灌装置的射程是10m,他能喷灌的面积是多少?
3.14×10?=314(m?)
答:他能喷灌的面积是314m?。
练习
小刚量得一棵树干的周长是125.6cm。这棵树干的横截面近似于圆,它的面积大约是多少?
3.14×(125.6÷3.14÷2)?=1256(cm?)
答:它的面积大约是1256cm?.
练习
右图是一块玉璧,外直径18cm,内直径7cm。这块玉璧的面积是多少?
3.14×[(18÷2)?-(7÷2)?]=215.875(cm?)
答:这块玉璧的面积是215.875cm?。
练习
右图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。
3.14×6?-3.14×(6÷2)?=84.78(cm?)
答:阴影部分的面积是84.78cm?。
练习
计算下面左边图形的周长和右边圆环的面积。
左图周长:
3.14×8×? ?+3.14×12×? ?+(12-8)=35.4(cm)
右图面积:
3.14×(12?-8?)=251.2(cm?)
练习
在你的生活里找找圆环形的物体,测量一下,再算算它的面积。
练习
右图中的铜钱直径28mm,中间的正方形边长为6mm。这个铜钱的面积是多少?
3.14×(28÷2)?-6×6=579.44(mm?)
答:这个铜钱的面积是579.44mm?。
练习
一个运动场如右图,两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?
周长:2×3.14×32+100×2=400.96(m)
面积:3.14×32?+100×(32×2)=9615.36(m?)
答:这个运动场的周长是400.96m,面积是9615.36m?。
练习
右图中的花瓣状门洞的边是由4个直径相等的半圆组成的。这个门洞的周长和面积分别是多少?
周长:3.14×1×2=6.28(m)
面积:3.14×(1÷2)?×2+1×1=2.57(m?)
答:这个门洞的周长是6.25m,面积是2.57m?。
练习
土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”,土楼的外围形状有圆形、方形、椭圆等。有两座地面是圆环形的土楼,其中一座外直径34m,内直径14m;另一座外直径26m,内直径也是14m。两座土楼的房屋占地面积相差多少?
3.14×[(34÷2)?-(14÷2)?]=753.6(m?)
3.14×[(26÷2)?-(14÷2)?]
=376.8(m?)
相差面积:753.6-376.8=376.8(m?)
答:两座土楼的房屋占地面积相差376.8m?。
练习
一个圆的周长是62.8m,半径增加了2m后,面积增加了多少?
62.8÷3.14÷2=10(m)
10+2=12(m)
3.14×(12?-10?)=138.16(m?)
答:面积增加了138.16m?。
练习
篮球场上的3分线是由两条平行线段和一个半圆组成的。请你根据图中的数据计算出3分线的长度和3分线内区域的面积。(得数保留两位小数。)
3分线的长度:
2×3.14×6.75×? ?+1.575×2
≈24.35(m)
3分线内区域的面积:
3.14×6.75?×? ?+6.75×2×1.575≈92.80(m?)
答:3分线长24.35m,3分线内区域的面积是92.80m?。
练习
在每个正方形中分别画一个最大的圆,并完成下表。
你发现了什么?请你自己再任意设定一个正方形的边长,在正方形中画一个最大的圆,看看能否也能得出相同的结论。
正方形的边长
正方形的面积
圆的面积
面积之比
200:157
1cm
2cm
3cm
4cm
1cm?
0.785cm?
200:157
200:157
4cm?
200:157
200:157
3.14cm?
7.065cm?
12.56cm?
19.625cm?
5cm
25cm?
16cm?
9cm?
练习
有一根绳子长31.4m,小红、小东和小林分别想用这根绳子在操场上围出一块地。怎样围面积最大?
答:当周长一定时,圆的面积最大,因此应该用这根绳子围成一个圆。
练习
为什么草原上蒙古包的底面是圆形的?为什么绝大多数的根和茎的横截面是圆形的?请你试着从数学的角度解释一下。
参考答案
答:当周长一定时,所有图形中圆的面积最大。蒙古包的底面做成圆形的,可以使居住的面积最大,绝大多数的根和茎的横截面是圆形的,可以最大面积地吸收水分。
提高练习
一个半径为6厘米的半圆形,在它的边界上任取不在一条直线上的三个点,以这三个点为顶点可以画出一个三角形.所有这样的三角形中,面积最大的是____平方厘米.
要想三角形的面积最大,则直径为底,半径为高.12×6÷2=36(平方厘米),所以最大的三角形面积是36平方厘米.
提高练习
将一个圆沿直径剪拼成一个近似的长方形,周长增加4厘米,这个圆的周长是____厘米,面积是____平方厘米.
r=4÷2=2(厘米),C=2πr=2× 3.14× 2=12.56(厘米),S=πr2=3.14× 22=12.56(平方厘米).
提高练习
一个圆的周长从6.28厘米,增加到12.56厘米,直径增加了____厘米,面积增加了____平方厘米.
原直径d1=6.28÷3.14=2(厘米),r1=2÷2=1(厘米),S1=πr12=3.14× 12=3.14(平方厘米),
现直径d2=12.56÷3.14=4(厘米),r2=4÷2=2(厘米),S2=πr22=3.14× 22=12.56(平方厘米),所以直径增加了4-2=2(厘米),面积增加了12.56-3.14=9.42(平方厘米).
提高练习
一个圆环,外圆周长25.12分米,内圆周长6.28分米,环形面积是____平方分米.
外圆半径:25.12÷3.14÷2=4(分米),
内圆半径:6.28÷3.14÷2=1(分米),
则环形面积为3.14×(4×4-1×1)=47.1(平方分米).
提高练习
一个圆环,外圆直径是20厘米,环宽2厘米,环形面积是____平方厘米.
R=20÷2=10(厘米),r=10-2=8(厘米),则环形面积为3.14×(10×10-8×8)=113.04(平方厘米).
提高练习
一个圆形花坛,它的半径是4米,沿着这个花坛的周长在里面铺了一圈宽1米的草皮,这圈草皮的面积是____平方米.
r=4-1=3(米),则这圈草皮的面积是3.14×(4×4-3×3)=21.98(平方米).
拓展练习
下图中四个圆的半径都是5厘米,阴影部分的面积是____平方厘米.
阴影部分的面积=3个圆的面积+(正方形的面积-1个圆的面积)=2个圆的面积+正方形的面积.
阴影部分的面积是2×3.14×5×5+10×10=257(平方厘米).
拓展练习
如图半圆的周长是25.7厘米,它的面积是______平方厘米.
半圆的半径是:25.7÷(3.14+2)=25.7÷5.14=5(厘米);所以半圆的面积是:3.14×52÷2=39.25(平方厘米).
拓展练习
草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见下图).这只羊能够活动的范围有____平方米.
所以这只羊能够活动的范围有2512平方米.
拓展练习
一个圆桌,桌面的周长是50.24分米,要在桌面上铺一块比桌面直径长4分米的圆形桌布,桌布的面积是____平方分米.
桌面直径是:50.24÷3.14=16(分米)
(16+4)÷2=10(分米),
则桌布面积为3.14×10×10=314(平方分米).
拓展练习
已知阴影部分的面积是5平方厘米,圆环的面积是____平方厘米.
圆环的面积是3.14×(R2-r2)=3.14×2×5=31.4(平方厘米)
拓展练习
已知阴影部分的面积是20平方厘米,圆环的面积是____平方厘米.
根据题意,得2R×R-2r×r=20,则圆环的面积是3.14×(R2-r2)=3.14×20÷2=31.4(平方厘米).
教学目标
使学生理解圆面积计算公式的推导过程,掌握圆面积计算公式。
使学生能利用圆面积的计算公式正确进行圆面积计算,并能解决有关圆面积的实际问题。
使学生理解圆环的形成,并能正确计算圆环面积。
教学重点
教学难点
圆面积的计算公式的推导。
理解圆的周长和半径与转化后近似长方形的长和宽的关系。
复习:什么叫平面图形的面积?
下列图形的面积是如何计算的?
a
a
a
a
a
a
b
h
h
h
b
S=ah
S=ah÷2
S=(a+b)h÷2
S=ab
圆所占平面的大小叫做圆的面积。
怎样计算一个圆的面积呢?
能不能和学过的图形联系起来呢?如果知道了圆的半径,可以计算出图中圆内外的两个正方形的面积,圆的面积介于这两个正方形面积之间。
如何得到一个圆的面积?想一想,并与同伴交流。
如何得到一个圆的面积?想一想,并与同伴交流。
如何得到一个圆的面积?想一想,并与同伴交流。
圆的面积是正方形面积(半径的平方)的3倍多一些。
r
o
圆面公式推导
观察下图,你有什么发现,完成填空后与同伴交流。
从上图中可以看出圆的半径是r,长方形的长近似(? ? ? ? ? ? ? ? ? ? ?),宽近似于(? ? ? ? ? ? ? ?)。
因为长方形的面积=(? ? ? )×(? ? ? )
所以圆面积=(? ? ?)×(? ? ?)=(? ? ? )
如果用S表示圆的面积,那么圆的面积计算公式就是 :
圆周长的一半
圆的半径
长
宽
πr
r
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆面公式推导
探索圆面积的计算方法
圆的面积
平行四边形的面积
平行四边形的面积=底×高
圆周长的一半
圆的面积
圆的半径
C÷2
底
r
高
×
πr
×
r
S=
圆面公式推导
探索圆面积的计算方法
C÷2
r
长
宽
圆的面积
长方形的面积
长方形的面积=底×高
圆周长的一半
圆的半径
×
πr
×
r
S=
圆的面积
例1
圆形草坪的直径是20 m,每平方米草皮8 元,铺满草坪需要多少钱?
从题目中你都知道了什么?
要求铺满草坪需要多少钱,先要求出圆形草坪的面积是多少平方米。
20÷2=10(m)
314×8=2512(元)
答:铺满草皮需要2512 元。
3.14×10?=314(m?)
做一做
一个圆形茶几桌面的直径是1 m,它的面积是多少平方米?
先求出半径,再求圆的面积。
1÷2=0.5(m)
3.14×0.5?=0.785(m?)
答:它的面积是0.785 m?。
圆环面积导入
求下面各圆的面积。(口头列式)
3.14×1 =3.14(平方厘米)
3.14×(4÷2) =12.56 (平方厘米)
2
2
圆环面积导入
仔细观察这些图案,你有什么发现?
例2
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
怎样利用内圆和外圆的面积求出圆环的面积?
3.14×6?-3.14×2?
=113.04-12.56
=100.48(cm?)
3.14×(6?-2?)
=3.14×32
=100.48(cm?)
还可以这样计算……
我是这样想的……
答:圆环的面积是100.48 cm?。
做一做
一个圆形环岛的直径是50 m,中间是一个直径为10 m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
要求草坪的占地面积,也就是求圆环的面积。
50÷2=25(m)? ? ? ? 10÷2=5(m)
3.14×(25?-5?)
=3.14×600
=1884(m?)
答:草坪的占地面积是1884 m?。
练习
完成下表。
4cm
50.24cm?
9cm
6cm
20cm
8cm
63.585cm?
28.26cm?
1256cm?
40cm
4.5cm
3cm
半径
直径
圆面积
练习
计算下面各圆的周长和面积。
左图:3.14×10=31.4(cm)
3.14×(10÷2)?=78.5(cm?)
右图:3.14×3×2=18.84(cm)
3.14×3?=28.26(cm?)
练习
公园草地上一个自动旋转喷灌装置的射程是10m,他能喷灌的面积是多少?
3.14×10?=314(m?)
答:他能喷灌的面积是314m?。
练习
小刚量得一棵树干的周长是125.6cm。这棵树干的横截面近似于圆,它的面积大约是多少?
3.14×(125.6÷3.14÷2)?=1256(cm?)
答:它的面积大约是1256cm?.
练习
右图是一块玉璧,外直径18cm,内直径7cm。这块玉璧的面积是多少?
3.14×[(18÷2)?-(7÷2)?]=215.875(cm?)
答:这块玉璧的面积是215.875cm?。
练习
右图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。
3.14×6?-3.14×(6÷2)?=84.78(cm?)
答:阴影部分的面积是84.78cm?。
练习
计算下面左边图形的周长和右边圆环的面积。
左图周长:
3.14×8×? ?+3.14×12×? ?+(12-8)=35.4(cm)
右图面积:
3.14×(12?-8?)=251.2(cm?)
练习
在你的生活里找找圆环形的物体,测量一下,再算算它的面积。
练习
右图中的铜钱直径28mm,中间的正方形边长为6mm。这个铜钱的面积是多少?
3.14×(28÷2)?-6×6=579.44(mm?)
答:这个铜钱的面积是579.44mm?。
练习
一个运动场如右图,两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?
周长:2×3.14×32+100×2=400.96(m)
面积:3.14×32?+100×(32×2)=9615.36(m?)
答:这个运动场的周长是400.96m,面积是9615.36m?。
练习
右图中的花瓣状门洞的边是由4个直径相等的半圆组成的。这个门洞的周长和面积分别是多少?
周长:3.14×1×2=6.28(m)
面积:3.14×(1÷2)?×2+1×1=2.57(m?)
答:这个门洞的周长是6.25m,面积是2.57m?。
练习
土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”,土楼的外围形状有圆形、方形、椭圆等。有两座地面是圆环形的土楼,其中一座外直径34m,内直径14m;另一座外直径26m,内直径也是14m。两座土楼的房屋占地面积相差多少?
3.14×[(34÷2)?-(14÷2)?]=753.6(m?)
3.14×[(26÷2)?-(14÷2)?]
=376.8(m?)
相差面积:753.6-376.8=376.8(m?)
答:两座土楼的房屋占地面积相差376.8m?。
练习
一个圆的周长是62.8m,半径增加了2m后,面积增加了多少?
62.8÷3.14÷2=10(m)
10+2=12(m)
3.14×(12?-10?)=138.16(m?)
答:面积增加了138.16m?。
练习
篮球场上的3分线是由两条平行线段和一个半圆组成的。请你根据图中的数据计算出3分线的长度和3分线内区域的面积。(得数保留两位小数。)
3分线的长度:
2×3.14×6.75×? ?+1.575×2
≈24.35(m)
3分线内区域的面积:
3.14×6.75?×? ?+6.75×2×1.575≈92.80(m?)
答:3分线长24.35m,3分线内区域的面积是92.80m?。
练习
在每个正方形中分别画一个最大的圆,并完成下表。
你发现了什么?请你自己再任意设定一个正方形的边长,在正方形中画一个最大的圆,看看能否也能得出相同的结论。
正方形的边长
正方形的面积
圆的面积
面积之比
200:157
1cm
2cm
3cm
4cm
1cm?
0.785cm?
200:157
200:157
4cm?
200:157
200:157
3.14cm?
7.065cm?
12.56cm?
19.625cm?
5cm
25cm?
16cm?
9cm?
练习
有一根绳子长31.4m,小红、小东和小林分别想用这根绳子在操场上围出一块地。怎样围面积最大?
答:当周长一定时,圆的面积最大,因此应该用这根绳子围成一个圆。
练习
为什么草原上蒙古包的底面是圆形的?为什么绝大多数的根和茎的横截面是圆形的?请你试着从数学的角度解释一下。
参考答案
答:当周长一定时,所有图形中圆的面积最大。蒙古包的底面做成圆形的,可以使居住的面积最大,绝大多数的根和茎的横截面是圆形的,可以最大面积地吸收水分。
提高练习
一个半径为6厘米的半圆形,在它的边界上任取不在一条直线上的三个点,以这三个点为顶点可以画出一个三角形.所有这样的三角形中,面积最大的是____平方厘米.
要想三角形的面积最大,则直径为底,半径为高.12×6÷2=36(平方厘米),所以最大的三角形面积是36平方厘米.
提高练习
将一个圆沿直径剪拼成一个近似的长方形,周长增加4厘米,这个圆的周长是____厘米,面积是____平方厘米.
r=4÷2=2(厘米),C=2πr=2× 3.14× 2=12.56(厘米),S=πr2=3.14× 22=12.56(平方厘米).
提高练习
一个圆的周长从6.28厘米,增加到12.56厘米,直径增加了____厘米,面积增加了____平方厘米.
原直径d1=6.28÷3.14=2(厘米),r1=2÷2=1(厘米),S1=πr12=3.14× 12=3.14(平方厘米),
现直径d2=12.56÷3.14=4(厘米),r2=4÷2=2(厘米),S2=πr22=3.14× 22=12.56(平方厘米),所以直径增加了4-2=2(厘米),面积增加了12.56-3.14=9.42(平方厘米).
提高练习
一个圆环,外圆周长25.12分米,内圆周长6.28分米,环形面积是____平方分米.
外圆半径:25.12÷3.14÷2=4(分米),
内圆半径:6.28÷3.14÷2=1(分米),
则环形面积为3.14×(4×4-1×1)=47.1(平方分米).
提高练习
一个圆环,外圆直径是20厘米,环宽2厘米,环形面积是____平方厘米.
R=20÷2=10(厘米),r=10-2=8(厘米),则环形面积为3.14×(10×10-8×8)=113.04(平方厘米).
提高练习
一个圆形花坛,它的半径是4米,沿着这个花坛的周长在里面铺了一圈宽1米的草皮,这圈草皮的面积是____平方米.
r=4-1=3(米),则这圈草皮的面积是3.14×(4×4-3×3)=21.98(平方米).
拓展练习
下图中四个圆的半径都是5厘米,阴影部分的面积是____平方厘米.
阴影部分的面积=3个圆的面积+(正方形的面积-1个圆的面积)=2个圆的面积+正方形的面积.
阴影部分的面积是2×3.14×5×5+10×10=257(平方厘米).
拓展练习
如图半圆的周长是25.7厘米,它的面积是______平方厘米.
半圆的半径是:25.7÷(3.14+2)=25.7÷5.14=5(厘米);所以半圆的面积是:3.14×52÷2=39.25(平方厘米).
拓展练习
草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见下图).这只羊能够活动的范围有____平方米.
所以这只羊能够活动的范围有2512平方米.
拓展练习
一个圆桌,桌面的周长是50.24分米,要在桌面上铺一块比桌面直径长4分米的圆形桌布,桌布的面积是____平方分米.
桌面直径是:50.24÷3.14=16(分米)
(16+4)÷2=10(分米),
则桌布面积为3.14×10×10=314(平方分米).
拓展练习
已知阴影部分的面积是5平方厘米,圆环的面积是____平方厘米.
圆环的面积是3.14×(R2-r2)=3.14×2×5=31.4(平方厘米)
拓展练习
已知阴影部分的面积是20平方厘米,圆环的面积是____平方厘米.
根据题意,得2R×R-2r×r=20,则圆环的面积是3.14×(R2-r2)=3.14×20÷2=31.4(平方厘米).
