六年级下册数学课件-圆柱的表面积 人教版(65张ppt)
文档属性
| 名称 | 六年级下册数学课件-圆柱的表面积 人教版(65张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 00:00:00 | ||
图片预览







文档简介
圆柱与圆锥
圆柱的表面积
(例3、例4)
教学目标
使学生理解和掌握圆柱体侧面积和表面积的计算方法,能正确运用公式计算圆柱的侧面积和表面积。?
培养学生观察、操作、概括的能力和利用所学知识合理灵活地分析、解决实际问题的能力。
培养学生的合作意识和主动探求知识的学习品质和实践能力。
教学重点
教学难点
圆柱表面积的计算。
圆柱体侧面积计算方法的推导。
开门见山
圆柱
圆柱的表面积指的是什么?
找一找
哪些物体的形状是圆柱?
在生活中,你还见过哪
些形状是圆柱的物体?
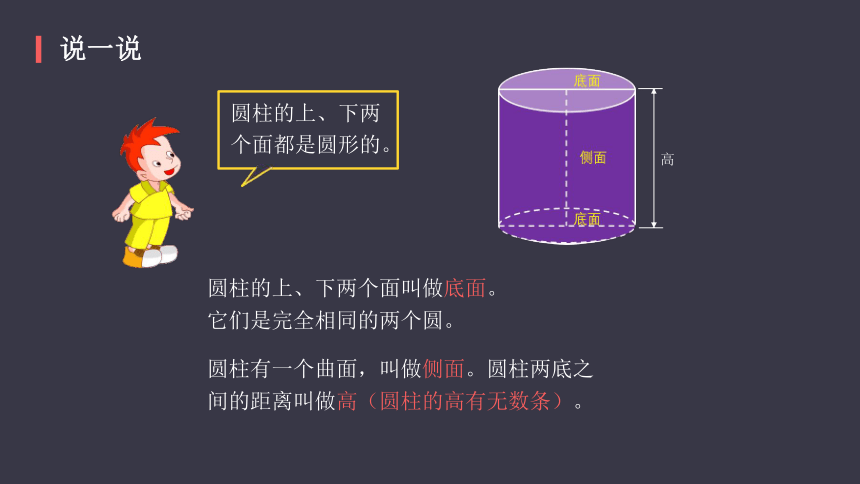
说一说
圆柱的上、下两
个面都是圆形的。
高
圆柱的上、下两个面叫做底面。它们是完全相同的两个圆。
圆柱有一个曲面,叫做侧面。圆柱两底之间的距离叫做高(圆柱的高有无数条)。
计算下面圆的周长和面积。
计算复习
d = 6 cm
r = 5 dm
周长:
面积:
周长:
面积:
3.14 × 6 = 18.84(cm)
3.14 ×? ? ? ? ? ? ? ? ?= 28.26(? ? ? )
2×3.14×5 = 31.4(cm)
3.14 ×? ? ?= 78.5(? ? ? )
计算复习
要牢记下面的计算公式
圆的周长
或
圆的面积
C = πd
C = 2πr
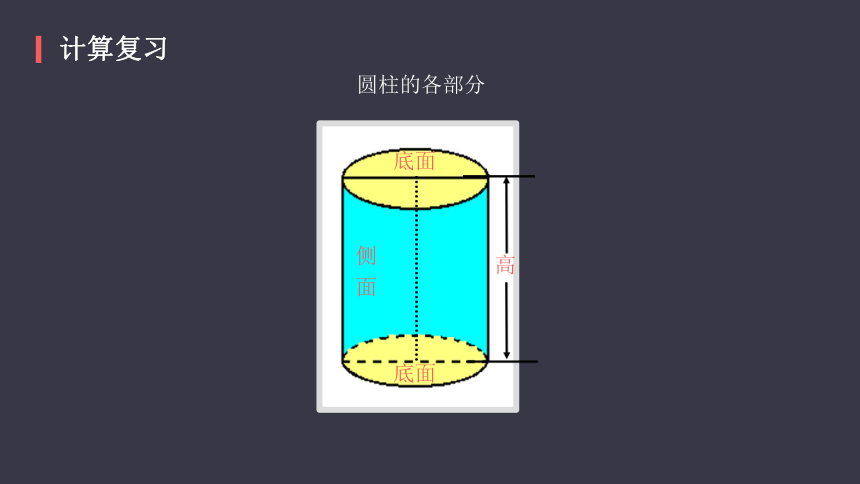
计算复习
圆柱的各部分
底面
底面
侧
面
高
知识点视频
圆柱的表面积
例三
例三
实 际 问 题
现在有一个罐头厂计划用铁皮制作一批底面半径?5?厘米,高?10?厘米的圆柱形罐头盒。你能不能帮厂长算一算制作一个至少需要多少平方厘米铁皮?
例三
底面周长
高
例三
底面
底面
圆柱的侧面
高
底面
底面
圆柱的侧面
高
例三
问题:圆柱的侧面展开
图中的长与圆柱底面的
周长有什么关系,宽与
圆柱的高有什么关系?
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
高
底面的周长
例三
圆柱的侧面积=底面周长×高
底面
底面
高
底面的周长
例三
侧面
底面
底面
圆柱的表面积=
圆柱的侧面积 + 两个底面的面积
底面周长×高
= 2πr × h + 2 ×?
例三
底面
底面
高
高
圆柱的表面积指的是侧面积与两个底面积的和。
请同学们看着圆柱表面展开的图形想一想:圆柱的表面积应该怎样计算?
圆柱的表面积=圆柱的侧面积+两个底面的面积
例三
高
高
圆柱的侧面是一个曲面,怎样计算它的面积呢?
想一想,能否将这个曲面转化成我们学过的平面图形?开动脑筋想一想它的侧面该怎样计算?
圆柱的侧面积=长方形的面积
=长 × 宽
=圆柱的底面周长 × 高
圆柱的侧面积=底面周长×高
要计算圆柱的侧面积需要知道哪两个条件?
用字母怎么表示呢?
用字母表示为:
直接计算:S =Ch
利用直径计算:S =πdh
利用半径计算:S =2πrh
例三
高
高
表面积和侧面积有什么不同?
侧面积是表面积的一部分,表面积还包含两个底面积。
表面积=侧面积+底面积×2
用字母公式表示:?
做一做
一个圆柱形茶叶桶的侧面贴着商标纸,圆柱底面半径是 5 cm,高是 20 cm。这张商标纸的面积是多少?
请你想一想,求商标纸的面积就是求什么?
2 × 3.14 × 5 × 20 = 628(? ? ? )?
答:这张商标纸的面积是 628? ? ? ? ?。
例四
一顶圆柱形厨师帽,高 30 cm,帽顶直径 20 cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成
想一想:求多少面料就是求什么?
“没有底”的帽子如果展开,它由哪几部分组成?
帽子的侧面积:3.14×20×30=1884(? ? ?)
帽顶的面积:3.14×(20÷2)=314(? ? ?)
需要用的面料:1884+314=2198≈2200(? ? ?)
答:做这样一顶帽子至少要用2200? ? ? ? 的面料。
实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。
做一做
1、求下面圆柱的侧面积。
底面周长是 1.6 m,高是 0.7 m。
底面半径是 3.2 dm,高是 5dm。
1.6 × 0.7 = 1.12(? ? )
答:圆柱的侧面积是 1.12? ? ? ?。
2 × 3.14 × 3.2 ×5 = 100.48(? ? ? )
答:圆柱的侧面积是 100.48? ? ? ? ?。
做一做
2、小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要多少彩纸?
请你想一想,求侧面积和一个底面积,需要知道哪两个条件?
笔筒的侧面积:3.14 × 8 × 13 = 326.56(? ? ?)
一个底面的面积:3.14 ×(8 ÷ 2)= 50.24 (? ? ?)
需要用的彩纸:326.56 + 50.24 = 376.8(? ? ?)
答:至少需要 376.8? ? ? ? ? 的彩纸。
基础练习
1、求下面罐头盒商标纸的面积。(接缝处忽略不计)(单位:厘米)
= ch
= 12 × 3.14 × 10
=376.8(平方厘米)
答:商标纸的面积是?376.8 平方厘米。
2、一个圆柱的底面半径是 10 厘米,高 30 厘米,它的表面积是多少平方厘米?
基础练习
侧面积:
底面积:
表面积:
答:它的表面积是2512平方厘米的。
2 × 3.14 × 10 × 30 = 1884(? ? ? )
3.14 × 102 × 2 = 628(? ? ? )
1884 + 628 = 2512(? ? ? )
基础练习
3、一顶圆柱形厨师帽,高 28 厘米,帽顶直径 20 厘米,做这样一顶帽子需要用多少面料(得数保留整十平方厘米)?
解:帽子的侧面积:
3.14 × 20 × 28 = 1758.4(平方厘米)
帽顶的面积:
3.14 ×? ? ? ? ? ? ? ? ? ?= 314(平方厘米)
需要用的面料:
1758.4 + 314 = 2072.4 ≈?2080(平方厘米)
答:做这样一顶帽子需要用2080平方厘米的面料。
提高练习
1.一台压路机的滚筒宽 1.2 米,直径为 0.8 米。如果它滚动 10 周,压路的面积是多少平方米?
=πdh
=3.14×0.8×1.2
=3.0144(? ?)
3.0144×10 =30.144 (? ?)?
答:如果它滚动 10 周,压路的面积是 30.144 平方米。
提高练习
2、一个圆柱体的侧面积是 72π? ? ? ?,底面半径 4 cm,它的高是多少?
解:72π ÷ (2 × π × 4)
? ? ?=72π ÷ 8π? ??
? ? ?=9(cm)
答:它的高是 9 cm。
提高练习
3.一个圆柱形水池,水池内壁和底部都镶上磁砖,水池内部底面周长 25.12 m,池深 1.2 m,镶磁砖的 面积是多少平方米?
侧面积:25.12 × 1.2 = 30.144
底面积:3.14 × (25.12 ÷ 3.14 ÷ 2)2 = 50.24
表面积:30.144 + 50.24 = 80.384
答:镶瓷砖的面积是 80.384 平方米。
4、一个圆柱体的底面积是 3 平方米,沿着底面将这个圆柱体横切成两个完全一样的小圆柱体,这两个小圆柱体的表面积比原来的圆柱体的表面积多了多少?
提高练习
3 × 2 = 6(平方米)
答:这两个小圆柱体的表面积比原来的圆柱体的表面积多了6平方米。
提高练习
5、一根圆柱形木材长 20 分米,把它截成 4 段,表面积增加了 18.84 平方分米。这根木材底面的面积是多少?
18.84 ÷ 3 ÷ 2 = 3.14(平方分米)
答:这根木材底面的面积是 3.14 平方分米。
拓展练习
1、一个圆柱体的侧面展开是个边长 9.42 cm 的正方形,这个圆柱体的表面积是多少? ? ? ? ?(得数保留两位小数)
解:9.42 × 9.42 + 3.14(9.42 ÷ 3.14 ÷ 2)2 × 2
= 88.728 + 14.13
≈ 102.86(? ? ? )
答:这个圆柱体的表面积是102.86? ? ? ? ?。
拓展练习
2、一个圆柱,如果它的高增加 2 米,它的表面积就增加 50.24 平方米,这个圆柱的底面积是多少平方米?
50.24 ÷ 2 ÷ 3.14 ÷ 2 = 4(米)
4 × 4 × 3.14 = 50.24(平方米)
答:这个圆柱体的底面积是 50.24 平方米。
拓展练习
3、一段圆柱体的木头高 8 厘米,底面周长 25.12 厘米。现在沿着它的底面直径垂直切开,表面积增加了多少平方厘米?
25.12 ÷ 3.14 = 8(厘米)
8 × 8 × 2 = 128(平方厘米)
答:表面积增加了 128 平方厘米。
4、如图所示,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱的底面半径是 10 厘米,那么原来长方形铁皮的面积是多少平方厘米?
拓展练习
10 × 2 = 20(厘米)
2 × 3.14 × 10 = 62.8(厘米)
(62.8 + 20 + 20)× 20 = 2056(平方厘米)
答:原来长方形铁皮的面积是 2056 平方厘米。
练习四
1、求下面各圆柱的表面积。(单位:cm)
底面积:3.14 ×? ? ? ? ? ? ? ?= 28.26(? ? ?) 侧面积:6 × 3.14 × 12 = 226.08 (? ? ?)
表面积:28.26 × 2 + 226.08 =? 282.6(? ? ?)
底面积:3.14 ×? ? ? ? ? ? ? ?=1256(? ? ?) 侧面积:40 × 3.14 × 3 = 376.8 (? ? ? )
表面积:1256 × 2 + 376.8 = 2888.8(? ? ?)
底面积:3.14 ×? ? ? ? ? ? ? ?=254.34(? ? ?) 侧面积18 × 3.14 × 15 = 847.8(? ? ?)
表面积:254.34 × 2 + 847.8 = 1356.48(? ? ?)? ?
练习四
2、一台压路机的前轮是圆柱形,轮宽 2 m,直径为 1.2 m。如果前轮转动一周,压路的面积是多少平方米?
一周压路的面积,实际上就是圆柱的测面积。
1.2 × 3.14 × 2 = 7.536(平方米)
答:压路的面积是 7.536 平方米。
练习四
3、广告公司制作了一个底面直径是 1.5 m、高 2.5 m的圆柱形灯箱。可以贴多大面积的海报?
求贴多大面积的海报,就是求这个灯箱的侧面积。
1.5 × 3.14 × 2.5 = 11.775(平方米)
答:可以贴面积是11.775平方米的海报。
练习四
4、修建一个圆柱形的沼气池,底面直径是 3 m,深 2 m。在池的四壁与下底面上,抹上水泥,抹水泥部分的面积是多少平方米?
底面积:3 ÷ 2 = 1.5(米)3.14 × 1.5 × 1.5 = 7.065(平方米)??
侧面积:3 × 3.14 × 2 = 18.84(平方米)
抹水泥部分的面积:18.84 + 7.065 = 25.905(平方米)
答:抹水泥部分的面积是 25.905 平方米。
练习四
5、某种饮料罐的形状为圆柱形,底面直径为 6 cm,高为 12 cm,将 24 罐这种饮料按如图所示的方式放入箱内,这个箱子的长、宽、高至少是多少厘米?
箱子的宽又与饮料罐的什么有关呢?
要想知道箱子的长,就要知道饮料罐的什么?
箱子的长:6 × 6 = 36(cm)
箱子的宽:6 × 4 = 24(cm)
箱子的高就是饮料罐的高,是 12 cm。
答:这个箱子的长是 36 cm,宽是 24 cm,高是 12 cm。
练习四
6、 求下面各图的表面积。
长方体的表面积:15 × 10 × 4 +10 × 10 × 2 = 800(? ? ?)
正方体的表面积:6 × 6 × 6 = 216(? ? ?)
圆柱的表面积:2 × 3.14 × 5 × 12 = 376.8(? ? ?)
3.14 ×? ? ?× 2 = 157 (? ? ?)?
376.8+157 = 533.8(? ? ?)
请你仔细观察,除了这样计算,还有其它计算方法吗?
6、 求下面各图的表面积。
练习四
长方体的表面积:10 × 4 × 15 +10 × 10 × 2 = 800(? ? ?)
正方体的表面积:6 × 4 × 6 + 6 × 6 × 2 = 216(? ? ?)
圆柱的表面积:2 × 3.14 × 5 × 12 = 376.8(? ? ?)?
3.14 ×? ? ?× 2 = 157 (? ? ?)?
376.8+157 = 533.8(? ? ?)
你有什么发现吗?
练习四
7、一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多?
黑布:20 × 3.14 × 10 + 3.14 ×? ? ? ? ? ? ? ?= 942(平方厘米)
红布:r : 20 ÷ 2 = 10(厘米) R :(10 + 20 + 10)÷ 2 = 20(厘米)
3.14 ×? ? ? ? 3.14 ×? ? ? ?= 942(平方厘米)
942 = 942
所以,两种布用的一样多。
练习四
8、王阿姨做了一个圆柱形的抱枕,长 80 cm,底面直径是 18 cm。如果侧面用花布,底面用黄色的布,两种布各需多少?
花布:18 × 3.14 × 80 = 4521.6(平方厘米)
黄色的布:3.14 ×? ? ? ? ? ? ? ? ?× 2 = 508.68(平方厘米)
答:花布需要 4521.6 平方厘米,黄色的布需要 508.68 平方厘米。
练习四
9、林叔叔做了一个圆柱形的灯笼,上下地面的中间分别留出了 78.5 平方厘米的口,他用了多少彩纸?
灯笼的侧面积:20 × 3.14 × 30 = 1884(平方厘米)
灯笼的底面积: 3.14 ×? ? ? ? ? ? ? ? ? 78.5 = 235.5(平方厘米)
彩纸: 235.5 × 2 + 1884 = 2355(平方厘米)
答:李叔叔用了 2355 平方厘米的彩纸。
练习四
10、一个圆柱形铁皮水桶(无盖),高 12 dm,底面直径是高的? ? ? 。做这个水桶大约要用多少铁皮?
底面直径:12 ×? ? ? = 9(分米)
底面半径:9 ÷ 2 = 4.5(分米)
侧面积:3.14 × 9 × 12 = 339.12(平方分米)
底面积:3.14 × 4.5 × 4.5 = 63.585(平方分米)
需要铁皮:63.585 + 339.12 = 402.705(平方分米)
答:做这个水桶大约需要铁皮 402.705 平方分米。
练习四
11.(1)要将路灯柱(如图)漆上白色的油漆,要漆多少平方米?? ?
? ? ?(2)街心花园有 30 个这样的灯柱,如果油漆灯柱每平方米人工费 5 元,? ? ? ? ? ? ? ? ?一共需要人工费多少元?
(1) 12 ÷ 2 = 6(厘米)
(16 × 12 + 16 × 12 + 12 × 12)× 2 - 3.14 × 62 =(192 + 192 + 144)× 2 - 113.04 = 1056 - 113.04 = 942.96(平方厘米)
3.14 × 12 × 55 = 3.14 × 660 = 2072.4(平方厘米)
942.96 + 2072.4 = 3015.36(平方厘米)= 0.301536(平方米)
答:要漆 0.301536 平方米;
(2)
0.301536 × 30 × 5 = 0.301536 ×150 ≈ 45.23(元)
答:一共需要人工费 45.23 元.
练习四
12、一个圆柱的侧面积是188.4? ? ? ? ?,底面半径是 2 dm。它的高是多少?
底面周长:2 × 3.14 × 2 = 12.56(分米)
高:188.4 ÷ 12.56 = 15(分米)
答:它的高是 15 分米。
练习四
13、一根圆柱形木料的底面半径是 0.3 m,长是 2 m。如图所示,将它截成 4 段,这些木料的表面积比原来增加了多少平方米?
木料的底面积:0.3 × 0.3 × 3.14 = 0.2826(平方米)
增加的表面积:0.2826 × 2 × 3 = 1.6956(平方米)
答:这些木料的表面积比原来增加了 1.6956 平方米。
14.、一个圆柱的侧面展开图是一个正方形,求这个圆柱的底面直径与高的比。
练习四
因为,这个圆柱的侧面展开图是一个正方形,所以正方形的边长为? ? ? ?。?
也就是圆柱的高为? ? ? ? 。
这个圆柱的底面直径与高的比为? ? ? ? ? ? ? ? ? ? ? ? ? 。
圆柱表面积其他公式的推导
达芬奇化圆为方
化圆为方,与三等分角、倍立方体并称古希腊三大几何作图问题。给定一个圆,它要求我们用圆规和直尺画出一个面积相等的正方形。这个坑一挖开,从古希腊到现在不断有人往里跳。直到解析几何的出现,人们才从根本上证明了这个问题的不可能性:化圆为方相当于作出 π 的平方根,但尺规作图只能进行四则运算和开平方,对作为超越数的 π 无能为力。但这并不能阻挡某些“数学爱好者”的脚步。至今仍有人往这个大坑里跳,而且摔得乐此不疲。
达芬奇化圆为方
有人跳坑,也就肯定有人耍点小聪明绕道而行。达·芬奇这位聪明人就想了一个很简单的办法:假设圆半径为 r,造一个半径为 r 高度为? ? ?的圆柱体,它的侧面面积恰好就是? ? ? ? 。接下来就好办了,用绳子把圆柱体的“腰围”和“身高”量一下,放到纸上形成一个矩形,然后用直尺圆规来将这个矩形化为正方形就好了。? ? ??
这个方法相当狡猾,用“度量”的方法巧妙避开了“作出 π 的平方根”这个问题。当然,在欧几里德这些希腊人的眼中,这种方法只是取巧,因为一来不精确,二来太犯规,用了直尺圆规以外的工具。即使用直尺和圆规来度量也不行,尺规作图的规定就是,直尺只能拿来画直线,圆规则是画圆,它们不能有“度量”的功能。
达·芬奇的“解法”
圆柱的表面积
(例3、例4)
教学目标
使学生理解和掌握圆柱体侧面积和表面积的计算方法,能正确运用公式计算圆柱的侧面积和表面积。?
培养学生观察、操作、概括的能力和利用所学知识合理灵活地分析、解决实际问题的能力。
培养学生的合作意识和主动探求知识的学习品质和实践能力。
教学重点
教学难点
圆柱表面积的计算。
圆柱体侧面积计算方法的推导。
开门见山
圆柱
圆柱的表面积指的是什么?
找一找
哪些物体的形状是圆柱?
在生活中,你还见过哪
些形状是圆柱的物体?
说一说
圆柱的上、下两
个面都是圆形的。
高
圆柱的上、下两个面叫做底面。它们是完全相同的两个圆。
圆柱有一个曲面,叫做侧面。圆柱两底之间的距离叫做高(圆柱的高有无数条)。
计算下面圆的周长和面积。
计算复习
d = 6 cm
r = 5 dm
周长:
面积:
周长:
面积:
3.14 × 6 = 18.84(cm)
3.14 ×? ? ? ? ? ? ? ? ?= 28.26(? ? ? )
2×3.14×5 = 31.4(cm)
3.14 ×? ? ?= 78.5(? ? ? )
计算复习
要牢记下面的计算公式
圆的周长
或
圆的面积
C = πd
C = 2πr
计算复习
圆柱的各部分
底面
底面
侧
面
高
知识点视频
圆柱的表面积
例三
例三
实 际 问 题
现在有一个罐头厂计划用铁皮制作一批底面半径?5?厘米,高?10?厘米的圆柱形罐头盒。你能不能帮厂长算一算制作一个至少需要多少平方厘米铁皮?
例三
底面周长
高
例三
底面
底面
圆柱的侧面
高
底面
底面
圆柱的侧面
高
例三
问题:圆柱的侧面展开
图中的长与圆柱底面的
周长有什么关系,宽与
圆柱的高有什么关系?
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
例三
底面
底面
高
底面的周长
例三
圆柱的侧面积=底面周长×高
底面
底面
高
底面的周长
例三
侧面
底面
底面
圆柱的表面积=
圆柱的侧面积 + 两个底面的面积
底面周长×高
= 2πr × h + 2 ×?
例三
底面
底面
高
高
圆柱的表面积指的是侧面积与两个底面积的和。
请同学们看着圆柱表面展开的图形想一想:圆柱的表面积应该怎样计算?
圆柱的表面积=圆柱的侧面积+两个底面的面积
例三
高
高
圆柱的侧面是一个曲面,怎样计算它的面积呢?
想一想,能否将这个曲面转化成我们学过的平面图形?开动脑筋想一想它的侧面该怎样计算?
圆柱的侧面积=长方形的面积
=长 × 宽
=圆柱的底面周长 × 高
圆柱的侧面积=底面周长×高
要计算圆柱的侧面积需要知道哪两个条件?
用字母怎么表示呢?
用字母表示为:
直接计算:S =Ch
利用直径计算:S =πdh
利用半径计算:S =2πrh
例三
高
高
表面积和侧面积有什么不同?
侧面积是表面积的一部分,表面积还包含两个底面积。
表面积=侧面积+底面积×2
用字母公式表示:?
做一做
一个圆柱形茶叶桶的侧面贴着商标纸,圆柱底面半径是 5 cm,高是 20 cm。这张商标纸的面积是多少?
请你想一想,求商标纸的面积就是求什么?
2 × 3.14 × 5 × 20 = 628(? ? ? )?
答:这张商标纸的面积是 628? ? ? ? ?。
例四
一顶圆柱形厨师帽,高 30 cm,帽顶直径 20 cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成
想一想:求多少面料就是求什么?
“没有底”的帽子如果展开,它由哪几部分组成?
帽子的侧面积:3.14×20×30=1884(? ? ?)
帽顶的面积:3.14×(20÷2)=314(? ? ?)
需要用的面料:1884+314=2198≈2200(? ? ?)
答:做这样一顶帽子至少要用2200? ? ? ? 的面料。
实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。
做一做
1、求下面圆柱的侧面积。
底面周长是 1.6 m,高是 0.7 m。
底面半径是 3.2 dm,高是 5dm。
1.6 × 0.7 = 1.12(? ? )
答:圆柱的侧面积是 1.12? ? ? ?。
2 × 3.14 × 3.2 ×5 = 100.48(? ? ? )
答:圆柱的侧面积是 100.48? ? ? ? ?。
做一做
2、小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要多少彩纸?
请你想一想,求侧面积和一个底面积,需要知道哪两个条件?
笔筒的侧面积:3.14 × 8 × 13 = 326.56(? ? ?)
一个底面的面积:3.14 ×(8 ÷ 2)= 50.24 (? ? ?)
需要用的彩纸:326.56 + 50.24 = 376.8(? ? ?)
答:至少需要 376.8? ? ? ? ? 的彩纸。
基础练习
1、求下面罐头盒商标纸的面积。(接缝处忽略不计)(单位:厘米)
= ch
= 12 × 3.14 × 10
=376.8(平方厘米)
答:商标纸的面积是?376.8 平方厘米。
2、一个圆柱的底面半径是 10 厘米,高 30 厘米,它的表面积是多少平方厘米?
基础练习
侧面积:
底面积:
表面积:
答:它的表面积是2512平方厘米的。
2 × 3.14 × 10 × 30 = 1884(? ? ? )
3.14 × 102 × 2 = 628(? ? ? )
1884 + 628 = 2512(? ? ? )
基础练习
3、一顶圆柱形厨师帽,高 28 厘米,帽顶直径 20 厘米,做这样一顶帽子需要用多少面料(得数保留整十平方厘米)?
解:帽子的侧面积:
3.14 × 20 × 28 = 1758.4(平方厘米)
帽顶的面积:
3.14 ×? ? ? ? ? ? ? ? ? ?= 314(平方厘米)
需要用的面料:
1758.4 + 314 = 2072.4 ≈?2080(平方厘米)
答:做这样一顶帽子需要用2080平方厘米的面料。
提高练习
1.一台压路机的滚筒宽 1.2 米,直径为 0.8 米。如果它滚动 10 周,压路的面积是多少平方米?
=πdh
=3.14×0.8×1.2
=3.0144(? ?)
3.0144×10 =30.144 (? ?)?
答:如果它滚动 10 周,压路的面积是 30.144 平方米。
提高练习
2、一个圆柱体的侧面积是 72π? ? ? ?,底面半径 4 cm,它的高是多少?
解:72π ÷ (2 × π × 4)
? ? ?=72π ÷ 8π? ??
? ? ?=9(cm)
答:它的高是 9 cm。
提高练习
3.一个圆柱形水池,水池内壁和底部都镶上磁砖,水池内部底面周长 25.12 m,池深 1.2 m,镶磁砖的 面积是多少平方米?
侧面积:25.12 × 1.2 = 30.144
底面积:3.14 × (25.12 ÷ 3.14 ÷ 2)2 = 50.24
表面积:30.144 + 50.24 = 80.384
答:镶瓷砖的面积是 80.384 平方米。
4、一个圆柱体的底面积是 3 平方米,沿着底面将这个圆柱体横切成两个完全一样的小圆柱体,这两个小圆柱体的表面积比原来的圆柱体的表面积多了多少?
提高练习
3 × 2 = 6(平方米)
答:这两个小圆柱体的表面积比原来的圆柱体的表面积多了6平方米。
提高练习
5、一根圆柱形木材长 20 分米,把它截成 4 段,表面积增加了 18.84 平方分米。这根木材底面的面积是多少?
18.84 ÷ 3 ÷ 2 = 3.14(平方分米)
答:这根木材底面的面积是 3.14 平方分米。
拓展练习
1、一个圆柱体的侧面展开是个边长 9.42 cm 的正方形,这个圆柱体的表面积是多少? ? ? ? ?(得数保留两位小数)
解:9.42 × 9.42 + 3.14(9.42 ÷ 3.14 ÷ 2)2 × 2
= 88.728 + 14.13
≈ 102.86(? ? ? )
答:这个圆柱体的表面积是102.86? ? ? ? ?。
拓展练习
2、一个圆柱,如果它的高增加 2 米,它的表面积就增加 50.24 平方米,这个圆柱的底面积是多少平方米?
50.24 ÷ 2 ÷ 3.14 ÷ 2 = 4(米)
4 × 4 × 3.14 = 50.24(平方米)
答:这个圆柱体的底面积是 50.24 平方米。
拓展练习
3、一段圆柱体的木头高 8 厘米,底面周长 25.12 厘米。现在沿着它的底面直径垂直切开,表面积增加了多少平方厘米?
25.12 ÷ 3.14 = 8(厘米)
8 × 8 × 2 = 128(平方厘米)
答:表面积增加了 128 平方厘米。
4、如图所示,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱的底面半径是 10 厘米,那么原来长方形铁皮的面积是多少平方厘米?
拓展练习
10 × 2 = 20(厘米)
2 × 3.14 × 10 = 62.8(厘米)
(62.8 + 20 + 20)× 20 = 2056(平方厘米)
答:原来长方形铁皮的面积是 2056 平方厘米。
练习四
1、求下面各圆柱的表面积。(单位:cm)
底面积:3.14 ×? ? ? ? ? ? ? ?= 28.26(? ? ?) 侧面积:6 × 3.14 × 12 = 226.08 (? ? ?)
表面积:28.26 × 2 + 226.08 =? 282.6(? ? ?)
底面积:3.14 ×? ? ? ? ? ? ? ?=1256(? ? ?) 侧面积:40 × 3.14 × 3 = 376.8 (? ? ? )
表面积:1256 × 2 + 376.8 = 2888.8(? ? ?)
底面积:3.14 ×? ? ? ? ? ? ? ?=254.34(? ? ?) 侧面积18 × 3.14 × 15 = 847.8(? ? ?)
表面积:254.34 × 2 + 847.8 = 1356.48(? ? ?)? ?
练习四
2、一台压路机的前轮是圆柱形,轮宽 2 m,直径为 1.2 m。如果前轮转动一周,压路的面积是多少平方米?
一周压路的面积,实际上就是圆柱的测面积。
1.2 × 3.14 × 2 = 7.536(平方米)
答:压路的面积是 7.536 平方米。
练习四
3、广告公司制作了一个底面直径是 1.5 m、高 2.5 m的圆柱形灯箱。可以贴多大面积的海报?
求贴多大面积的海报,就是求这个灯箱的侧面积。
1.5 × 3.14 × 2.5 = 11.775(平方米)
答:可以贴面积是11.775平方米的海报。
练习四
4、修建一个圆柱形的沼气池,底面直径是 3 m,深 2 m。在池的四壁与下底面上,抹上水泥,抹水泥部分的面积是多少平方米?
底面积:3 ÷ 2 = 1.5(米)3.14 × 1.5 × 1.5 = 7.065(平方米)??
侧面积:3 × 3.14 × 2 = 18.84(平方米)
抹水泥部分的面积:18.84 + 7.065 = 25.905(平方米)
答:抹水泥部分的面积是 25.905 平方米。
练习四
5、某种饮料罐的形状为圆柱形,底面直径为 6 cm,高为 12 cm,将 24 罐这种饮料按如图所示的方式放入箱内,这个箱子的长、宽、高至少是多少厘米?
箱子的宽又与饮料罐的什么有关呢?
要想知道箱子的长,就要知道饮料罐的什么?
箱子的长:6 × 6 = 36(cm)
箱子的宽:6 × 4 = 24(cm)
箱子的高就是饮料罐的高,是 12 cm。
答:这个箱子的长是 36 cm,宽是 24 cm,高是 12 cm。
练习四
6、 求下面各图的表面积。
长方体的表面积:15 × 10 × 4 +10 × 10 × 2 = 800(? ? ?)
正方体的表面积:6 × 6 × 6 = 216(? ? ?)
圆柱的表面积:2 × 3.14 × 5 × 12 = 376.8(? ? ?)
3.14 ×? ? ?× 2 = 157 (? ? ?)?
376.8+157 = 533.8(? ? ?)
请你仔细观察,除了这样计算,还有其它计算方法吗?
6、 求下面各图的表面积。
练习四
长方体的表面积:10 × 4 × 15 +10 × 10 × 2 = 800(? ? ?)
正方体的表面积:6 × 4 × 6 + 6 × 6 × 2 = 216(? ? ?)
圆柱的表面积:2 × 3.14 × 5 × 12 = 376.8(? ? ?)?
3.14 ×? ? ?× 2 = 157 (? ? ?)?
376.8+157 = 533.8(? ? ?)
你有什么发现吗?
练习四
7、一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多?
黑布:20 × 3.14 × 10 + 3.14 ×? ? ? ? ? ? ? ?= 942(平方厘米)
红布:r : 20 ÷ 2 = 10(厘米) R :(10 + 20 + 10)÷ 2 = 20(厘米)
3.14 ×? ? ? ? 3.14 ×? ? ? ?= 942(平方厘米)
942 = 942
所以,两种布用的一样多。
练习四
8、王阿姨做了一个圆柱形的抱枕,长 80 cm,底面直径是 18 cm。如果侧面用花布,底面用黄色的布,两种布各需多少?
花布:18 × 3.14 × 80 = 4521.6(平方厘米)
黄色的布:3.14 ×? ? ? ? ? ? ? ? ?× 2 = 508.68(平方厘米)
答:花布需要 4521.6 平方厘米,黄色的布需要 508.68 平方厘米。
练习四
9、林叔叔做了一个圆柱形的灯笼,上下地面的中间分别留出了 78.5 平方厘米的口,他用了多少彩纸?
灯笼的侧面积:20 × 3.14 × 30 = 1884(平方厘米)
灯笼的底面积: 3.14 ×? ? ? ? ? ? ? ? ? 78.5 = 235.5(平方厘米)
彩纸: 235.5 × 2 + 1884 = 2355(平方厘米)
答:李叔叔用了 2355 平方厘米的彩纸。
练习四
10、一个圆柱形铁皮水桶(无盖),高 12 dm,底面直径是高的? ? ? 。做这个水桶大约要用多少铁皮?
底面直径:12 ×? ? ? = 9(分米)
底面半径:9 ÷ 2 = 4.5(分米)
侧面积:3.14 × 9 × 12 = 339.12(平方分米)
底面积:3.14 × 4.5 × 4.5 = 63.585(平方分米)
需要铁皮:63.585 + 339.12 = 402.705(平方分米)
答:做这个水桶大约需要铁皮 402.705 平方分米。
练习四
11.(1)要将路灯柱(如图)漆上白色的油漆,要漆多少平方米?? ?
? ? ?(2)街心花园有 30 个这样的灯柱,如果油漆灯柱每平方米人工费 5 元,? ? ? ? ? ? ? ? ?一共需要人工费多少元?
(1) 12 ÷ 2 = 6(厘米)
(16 × 12 + 16 × 12 + 12 × 12)× 2 - 3.14 × 62 =(192 + 192 + 144)× 2 - 113.04 = 1056 - 113.04 = 942.96(平方厘米)
3.14 × 12 × 55 = 3.14 × 660 = 2072.4(平方厘米)
942.96 + 2072.4 = 3015.36(平方厘米)= 0.301536(平方米)
答:要漆 0.301536 平方米;
(2)
0.301536 × 30 × 5 = 0.301536 ×150 ≈ 45.23(元)
答:一共需要人工费 45.23 元.
练习四
12、一个圆柱的侧面积是188.4? ? ? ? ?,底面半径是 2 dm。它的高是多少?
底面周长:2 × 3.14 × 2 = 12.56(分米)
高:188.4 ÷ 12.56 = 15(分米)
答:它的高是 15 分米。
练习四
13、一根圆柱形木料的底面半径是 0.3 m,长是 2 m。如图所示,将它截成 4 段,这些木料的表面积比原来增加了多少平方米?
木料的底面积:0.3 × 0.3 × 3.14 = 0.2826(平方米)
增加的表面积:0.2826 × 2 × 3 = 1.6956(平方米)
答:这些木料的表面积比原来增加了 1.6956 平方米。
14.、一个圆柱的侧面展开图是一个正方形,求这个圆柱的底面直径与高的比。
练习四
因为,这个圆柱的侧面展开图是一个正方形,所以正方形的边长为? ? ? ?。?
也就是圆柱的高为? ? ? ? 。
这个圆柱的底面直径与高的比为? ? ? ? ? ? ? ? ? ? ? ? ? 。
圆柱表面积其他公式的推导
达芬奇化圆为方
化圆为方,与三等分角、倍立方体并称古希腊三大几何作图问题。给定一个圆,它要求我们用圆规和直尺画出一个面积相等的正方形。这个坑一挖开,从古希腊到现在不断有人往里跳。直到解析几何的出现,人们才从根本上证明了这个问题的不可能性:化圆为方相当于作出 π 的平方根,但尺规作图只能进行四则运算和开平方,对作为超越数的 π 无能为力。但这并不能阻挡某些“数学爱好者”的脚步。至今仍有人往这个大坑里跳,而且摔得乐此不疲。
达芬奇化圆为方
有人跳坑,也就肯定有人耍点小聪明绕道而行。达·芬奇这位聪明人就想了一个很简单的办法:假设圆半径为 r,造一个半径为 r 高度为? ? ?的圆柱体,它的侧面面积恰好就是? ? ? ? 。接下来就好办了,用绳子把圆柱体的“腰围”和“身高”量一下,放到纸上形成一个矩形,然后用直尺圆规来将这个矩形化为正方形就好了。? ? ??
这个方法相当狡猾,用“度量”的方法巧妙避开了“作出 π 的平方根”这个问题。当然,在欧几里德这些希腊人的眼中,这种方法只是取巧,因为一来不精确,二来太犯规,用了直尺圆规以外的工具。即使用直尺和圆规来度量也不行,尺规作图的规定就是,直尺只能拿来画直线,圆规则是画圆,它们不能有“度量”的功能。
达·芬奇的“解法”
