六年级下册数学课件-圆锥的体积 人教版(64张ppt)
文档属性
| 名称 | 六年级下册数学课件-圆锥的体积 人教版(64张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 00:00:00 | ||
图片预览







文档简介
圆锥的体积
(例2、例3)
能够正确运用圆锥体积计算公式解决实际有关圆锥体积的实际应用问题。
教学目标
在探作中完成圆锥体积公式的推导。在合作探究中探明等底等高圆柱体积与圆锥体积内在联系。
在探索合作中感受教学与我生活的密切联系,让学生感受探究成功的快乐。
教学重点
掌握圆锥体积的计算公式,并能灵活利用公式求圆锥的体积。
教学难点
理解圆锥体积公式的推导过程及解决生活中的实际问题。
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
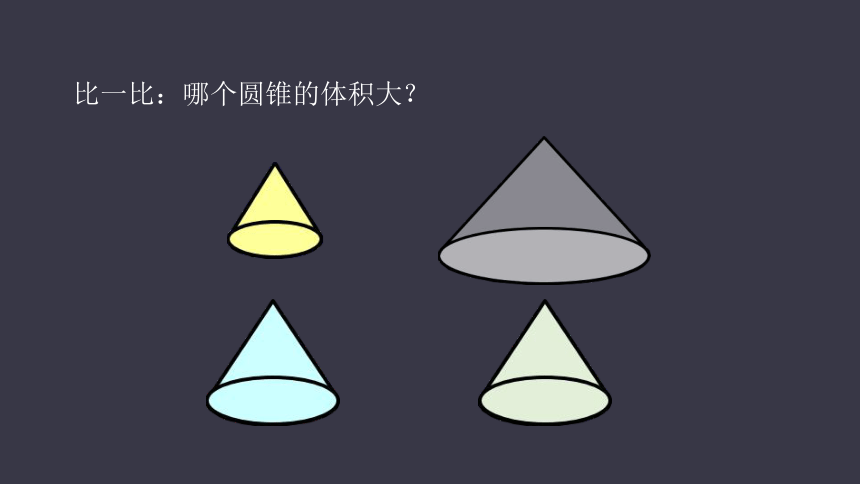
比一比:哪个圆锥的体积大?
1.怎样计算圆柱的体积?
V=Sh=πr??h
?
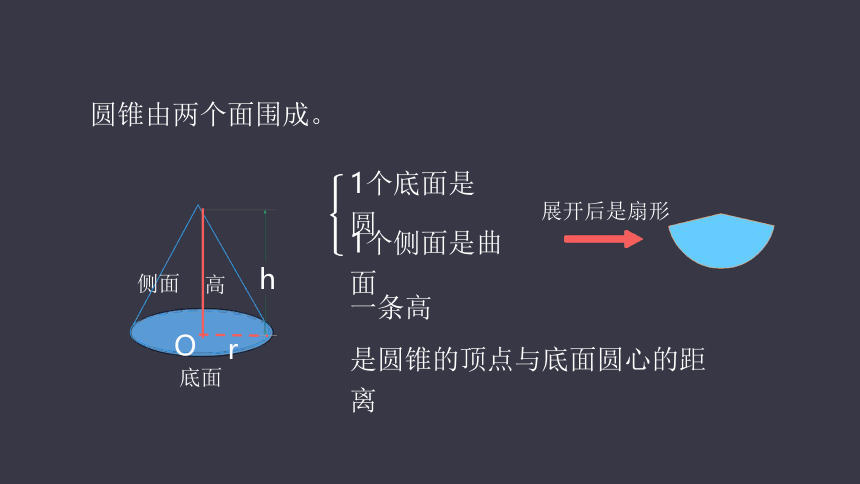
圆锥由两个面围成。
1个底面是圆
1个侧面是曲面
一条高
是圆锥的顶点与底面圆心的距离
展开后是扇形
底面
高
h
O
r
侧面
如何计算圆锥的体积呢?
圆柱的底面是圆,圆锥的底面也是圆。
你能猜测一下等底、等高的圆柱和圆锥的体积之间的关系吗?
圆锥的体积与圆柱的体积有没有关系呢?
例2
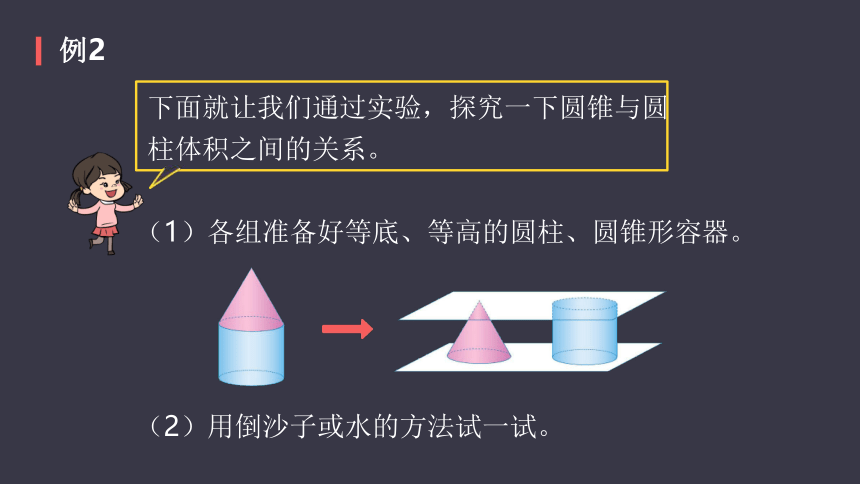
下面就让我们通过实验,探究一下圆锥与圆柱体积之间的关系。
例2
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
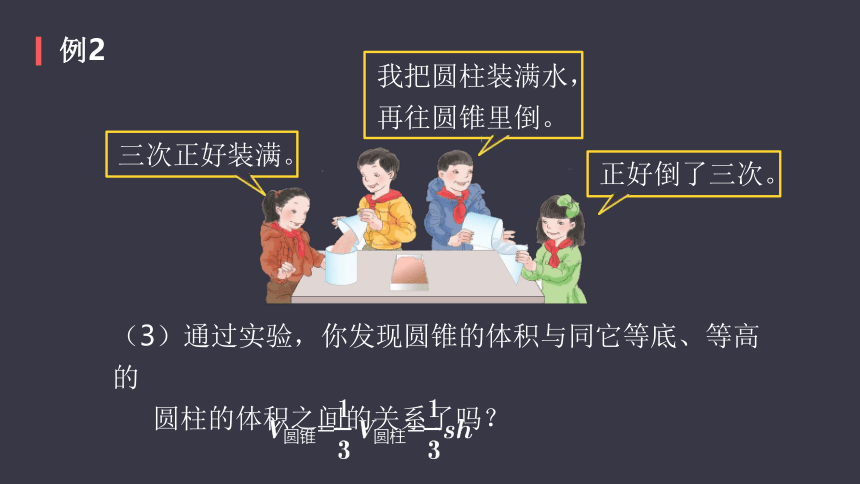
正好倒了三次。
我把圆柱装满水,
再往圆锥里倒。
三次正好装满。
例2
(3)通过实验,你发现圆锥的体积与同它等底、等高的
圆柱的体积之间的关系了吗?
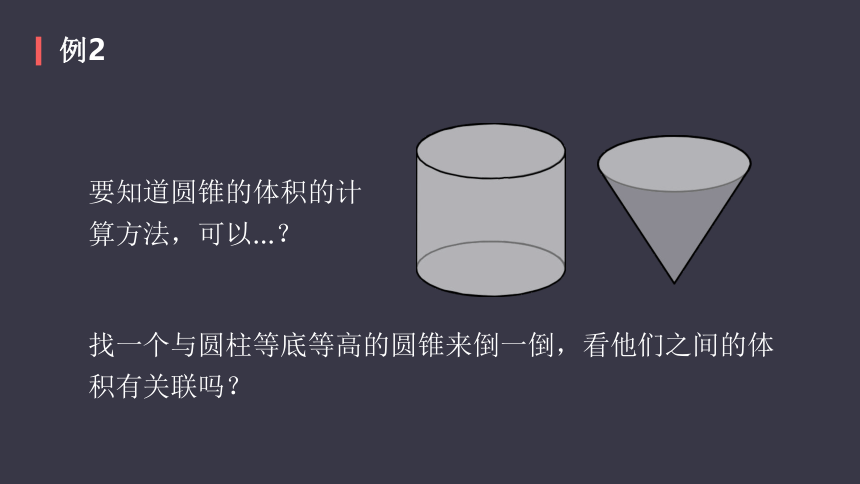
要知道圆锥的体积的计算方法,可以…?
找一个与圆柱等底等高的圆锥来倒一倒,看他们之间的体积有关联吗?
例2
找一个与圆柱等底等高的圆锥来倒一倒。
例2
例2
例2
例2
例2
例2
例2
例2
例2
例2
例2
结论:圆柱体积是等底等高圆锥体积的3倍 ,即圆锥体积是等底等高圆柱体积的? ? ?。
例2
等
高
等
底
V柱=Sh
V锥=? ? ?Sh
例2
推导公式:
小结
圆锥的体积等于和它等底等高的圆柱体积的三分之一
例2
问题
探究
练习
拓展
圆锥的体积
圆锥的体积
圆锥的体积
这堆小麦的体积是多少呢?
好大的一堆小麦
实际是求圆锥的体积
V=sh
?
按照下面方法做一做,你有什么发现?
圆锥的体积
圆柱的体积等于和它等底等高的圆锥的体积的3倍。
准备等底等高的圆柱形容器和圆锥形容器各一个。
将圆锥形容器装满沙子,再倒入圆柱形容器,看几次能倒满。
如果小麦堆的底面半径为2m,高为1.5m。小麦堆的体积是多少立方米?
圆锥的体积
答:小麦堆的体积是 ? ? ? ? ? ? ? 。
1.下图中,圆锥的体积与哪个圆柱的体积相等?说 说你是怎么想的。
练一练
2.计算下面各圆锥的体积。
练一练
3.如图,测量中经常使用铅锤。这个铅锤的体积是多少立方厘米?
练一练
4.有一座圆锥形帐篷,底面直径约5m,高约3.6m。
⑴ 它的占地面积约是多少平方米?
⑵ 它内部的空间约是多少立方米?
练一练
5.张大伯家有一堆小麦,堆成了圆锥形,张大伯量 得它的底面周长是9.42m,高是2m,这堆小麦的 体积是多少立方米?如果每立方米小麦的质量为 700kg,这堆小麦约重约重多少千克?
练一练
底面积:3.14×(9.42÷3.14÷2)
体积:
质量:
4.71×700=3297(kg)
6.一个圆柱形橡皮泥,底面积是12cm2,高是5cm。??
(1)如果把它捏成同样底面大小的圆锥,这个圆锥的高是多少???
(2) 如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
练一练
5×3=15(cm)
你学到了什么?
要求出这堆沙子大约重多少吨,就要先求什么?
就要先求出这堆沙的体积,也就是圆锥的体积。
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?(得数保留两位小数。)
例3
(1)沙堆底面积:
3.14 × ? ? ? ? ? ? ?=3.14×4=12.56
(2)沙堆的体积:
×12.56×1.2=5.024≈5.02
(3)沙堆重:
5.02×1.5=7.53(t)
答:这堆沙子大约重7.53吨。
1. 一个圆锥形的零件,底面积是19cm2,高是12cm, 这个零件的体积是多少?
做一做
答:这个零件的体积是76cm? 。
×19 ×12=76(cm )
?
?
2. 一个用钢铸造成的圆锥形铅锤,底面直径是4cm,?高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数)
做一做
(1)铅锤底面积:
3.14 × ? ? ? ? ? ? ?=3.14×4=12.56
(2)铅锤的体积:
×12.56×5≈21
(3)铅锤的质量:
21×7.8≈163(g)
答:这个铅锤大约重163克 。
判断:
1. 圆柱体的体积一定比圆锥体的体积大( ? ? ? )
2. 圆锥的体积等于和它等底等高的圆柱体积的_x0010_ 。 ( ? ? ?)
3. 正方体、长方体、圆锥体的体积都等于底面积×高。 ( ? ? ?)
4. 等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那
么圆锥的体积是9立方米( ? ? ? )
基础练习
2、只列式不计算:
求下面各圆锥的体积 .
基础练习
①底面面积是7.8平方米,高是1.8米。
列式:___________________
②底面半径是4厘米,高是21厘米。
③底面直径是6分米,高是6分米。
列式:___________________
列式:___________________
基础练习
填表:
已 知 条 件
体积
圆锥底面积15平方厘米,高8厘米
圆锥底面半径3分米,高5分米
圆锥底面直径4米,高6米
40立方厘米
47.1立方分米
25.12立方米
1、一个近似于圆锥的沙堆,测得底面直径是4米,高是1.5米。每立方米沙约重1.5吨,这堆沙约重多少吨?
提高练习
答:这堆沙约重9.42吨。
2.有一座圆锥形帐篷,底面直径约5m,高约3.6m。??
(1)它的占地面积约是多少平方米???
(2) 它内部的空间约是多少立方米?
提高练习
3.一个圆柱形橡皮泥,底面积是12cm ,高是5cm。??
(1)如果把它捏成同样底面大小的圆锥,这个圆锥的高是多少?
(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
提高练习
5×3=15(cm)
2
1.如下图,绿色部分的体积相当于整个物体体积的(? ? ? ?)分之(? ? ? ).
拓展练习
五
二
a
a
a
2、 一个圆锥体,如果高不变,底面积半径 扩大3倍,那么体积将( ? ? ? ? )。
A、扩大3倍 ? ? ? ? ?B、扩大9倍 ? ? ? ? ? ? ?C、扩大6倍
拓展练习
B
3、如图,三角形以AB为轴旋转后所得到的仿锤体的体积是多少?
拓展练习
(3.14×5×5×20+3.14×5×5×10)=785(立方厘米)
下边沙子体积是上边沙子体积的几倍?
拓展练习
下边沙子体积是上边
沙子体积的7倍。
3厘米
3厘米
4. 填空
练习六
(1)一个圆柱的体积是75.36m?,与它等底等高的圆锥的体积是( ? ? ? ? ? )m?。
25.12
(2)一个圆锥的体积是141.3m?,与它等底等高的圆柱的体积是( ? ? ? ? ? )m?。
423.9
5、判断下面的说法是不是正确。
练习六
(1)圆锥的体积等于圆柱体积的? ? ?。( ? ?)
(2)圆柱的体积大于与它等底等高的圆锥的体积。(? ? )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。(? ? )
6、一个圆锥的底面周长是31.4厘米,高是9厘米,它的体积
是多少?
练习六
半径:31.4÷3.14÷2=5(厘米)
体积:? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 235.5(立方厘米)
答:它的体积是235.5立方厘米。
7、一堆煤成圆锥形,高2m,底面周长为18.84m。这堆煤的
体积大约是多少?已知每立方米的煤越重1.4t,这堆煤大约重
多少吨?(得数保留整数)
练习六
半径:18.84÷3.14÷2=3(米)
体积:? ? ? ? ? ? ? ? ? ? ? ? ? ?=18.84(立方米)
大约重:1.4×18.84=26.376≈26(吨)
答:这堆煤的体积大约是18.84立方米,大约重26吨。
8、小明家去年秋季收获的稻谷堆成了圆锥形,高1m,底面直径2m。
(1)这堆稻谷的体积是多少?(保留两位小数)
(2)如果每立方米的稻谷重650kg,这堆稻谷重多少千克?
(3)小明家有0.25公顷稻田,平均每公顷产稻谷多少千克?
(4)如果每千克稻谷售价2.8元,这些稻谷能卖多少钱?
练习六
≈1.05(立方米)
(2)1.05×650=682.5(千克)
(3)682.5÷0.25=2730(千克)
(4)682.5×2.8=1911(元)
(1)
9. 一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
练习六
想一想,当一个圆柱与一个圆锥的底面积和体积分别相等时,圆锥的高与圆柱的高又是什么关系呢?
4×3=12(dm)
答:圆锥的高是12dm 。
10、一个圆柱与圆锥的体积和高分别相等,已知圆锥的底面积
是28.26平方米,圆柱的底面积是多少?
练习六
在等高等体积的前提下,圆柱底面积是圆锥底面积的三分之一,故而 28.26? ? ? ? ?=9.42(平方米)
11、一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失的情况下所积的深度,称为降水量(通常以毫米为单位)。
测定降水量常用的仪器包括雨量器和量筒.我国气象规定,按
24小时的降水量为标准,降水级别如表.
练习六
级别
降水量
/mm
小雨
中雨
大雨
暴雨
大暴雨
特大暴雨
10以下
10~24.9
25~49.9? ? ?50~99.9
100~199.9
200以上
练习六
某区的土地面积为 ? ? ? ? ? ? ? ? ?,2012年7月23日平均降水量为220mm,改日该地区总降水为多少亿立方米?该区一年绿化
用水 为0.4亿立方米,这些雨水的20%能满足绿化用说吗?
1000平方千米=1000000000(平方米)
220×1000000000=220000000000(立方毫米)=2.2(亿立方米)
2.2×20%=0.44(亿立方米)
0.44>0.4
答:这些雨水的20%能满足绿化用水.
度量棱锥的体积
棱锥的体积
将棱锥放入一个底面相同、高度相等的盒子里。棱锥体占据了
整个盒子体积的几分之几?
这是一个相当困难的问题,同时也是相当古老,其历史可以上
溯到古埃及。
? ? 首先,我们很聪明地注意到,如果连接立方体的中心和它的
八个顶点,那么我们就可以将立方体切分成几个棱锥体。
棱锥的体积
? ? 由于立方体的每一个面都对应着一个棱锥体,所以一共有六
个这样的棱锥体。又由于所有的棱锥体都是相同的,所以每一个
棱锥体的体积都是立方体的六分之一。
? ? 截得这个正方体的的一半,可以发现每一个棱锥体的体积都
是这个长方体体积的三分之一。
? ? 然而这一存在一个问题,那就是我们得到的结论仅仅适用于某些特殊形状的棱锥体(其高度正好是它的底面边长的一半)。而大部分的棱锥体并不能刚好组合成立方体或其他规整的形状,它们不是太尖锐就是太平缓。
棱锥的体积
? ? 这是否意味着我们只能度量某些特殊形状的棱锥体呢?幸运的是,实际上并不是这样!这里关键的一点是,如果对特殊的棱锥体进行适当的拉伸变换,我们就可以得到任何形状的棱锥体。例如,如果你想要一个比较尖锐的棱锥
体,我们就可以在垂直方向上对它进行任何
系数的拉伸变换,直到得到我们想要的高度。
这就是最有意思的事,那就是拉伸变换对棱锥体体积所造成的影响和所装盒子的体积的影响是一样的,两者的体积都扩大了拉伸系数倍。这说明两者的体积之比没有发生变化。既然对特殊形状的棱锥体来说,该比值是三分之一,那么对于任何形状的棱锥体来说,该比值也必然是三分之一。因此我们得到结论:任何棱锥体的体积都是刚好装载它的盒子体积的三分之一,也就是它等底等高柱体体积的三分之一。
棱锥的体积
这些知识将在我们中学的学习中继续学习的。
圆锥的体积
(例2、例3)
能够正确运用圆锥体积计算公式解决实际有关圆锥体积的实际应用问题。
教学目标
在探作中完成圆锥体积公式的推导。在合作探究中探明等底等高圆柱体积与圆锥体积内在联系。
在探索合作中感受教学与我生活的密切联系,让学生感受探究成功的快乐。
教学重点
掌握圆锥体积的计算公式,并能灵活利用公式求圆锥的体积。
教学难点
理解圆锥体积公式的推导过程及解决生活中的实际问题。
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
比一比:哪个圆锥的体积大?
1.怎样计算圆柱的体积?
V=Sh=πr??h
?
圆锥由两个面围成。
1个底面是圆
1个侧面是曲面
一条高
是圆锥的顶点与底面圆心的距离
展开后是扇形
底面
高
h
O
r
侧面
如何计算圆锥的体积呢?
圆柱的底面是圆,圆锥的底面也是圆。
你能猜测一下等底、等高的圆柱和圆锥的体积之间的关系吗?
圆锥的体积与圆柱的体积有没有关系呢?
例2
下面就让我们通过实验,探究一下圆锥与圆柱体积之间的关系。
例2
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
正好倒了三次。
我把圆柱装满水,
再往圆锥里倒。
三次正好装满。
例2
(3)通过实验,你发现圆锥的体积与同它等底、等高的
圆柱的体积之间的关系了吗?
要知道圆锥的体积的计算方法,可以…?
找一个与圆柱等底等高的圆锥来倒一倒,看他们之间的体积有关联吗?
例2
找一个与圆柱等底等高的圆锥来倒一倒。
例2
例2
例2
例2
例2
例2
例2
例2
例2
例2
例2
结论:圆柱体积是等底等高圆锥体积的3倍 ,即圆锥体积是等底等高圆柱体积的? ? ?。
例2
等
高
等
底
V柱=Sh
V锥=? ? ?Sh
例2
推导公式:
小结
圆锥的体积等于和它等底等高的圆柱体积的三分之一
例2
问题
探究
练习
拓展
圆锥的体积
圆锥的体积
圆锥的体积
这堆小麦的体积是多少呢?
好大的一堆小麦
实际是求圆锥的体积
V=sh
?
按照下面方法做一做,你有什么发现?
圆锥的体积
圆柱的体积等于和它等底等高的圆锥的体积的3倍。
准备等底等高的圆柱形容器和圆锥形容器各一个。
将圆锥形容器装满沙子,再倒入圆柱形容器,看几次能倒满。
如果小麦堆的底面半径为2m,高为1.5m。小麦堆的体积是多少立方米?
圆锥的体积
答:小麦堆的体积是 ? ? ? ? ? ? ? 。
1.下图中,圆锥的体积与哪个圆柱的体积相等?说 说你是怎么想的。
练一练
2.计算下面各圆锥的体积。
练一练
3.如图,测量中经常使用铅锤。这个铅锤的体积是多少立方厘米?
练一练
4.有一座圆锥形帐篷,底面直径约5m,高约3.6m。
⑴ 它的占地面积约是多少平方米?
⑵ 它内部的空间约是多少立方米?
练一练
5.张大伯家有一堆小麦,堆成了圆锥形,张大伯量 得它的底面周长是9.42m,高是2m,这堆小麦的 体积是多少立方米?如果每立方米小麦的质量为 700kg,这堆小麦约重约重多少千克?
练一练
底面积:3.14×(9.42÷3.14÷2)
体积:
质量:
4.71×700=3297(kg)
6.一个圆柱形橡皮泥,底面积是12cm2,高是5cm。??
(1)如果把它捏成同样底面大小的圆锥,这个圆锥的高是多少???
(2) 如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
练一练
5×3=15(cm)
你学到了什么?
要求出这堆沙子大约重多少吨,就要先求什么?
就要先求出这堆沙的体积,也就是圆锥的体积。
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?(得数保留两位小数。)
例3
(1)沙堆底面积:
3.14 × ? ? ? ? ? ? ?=3.14×4=12.56
(2)沙堆的体积:
×12.56×1.2=5.024≈5.02
(3)沙堆重:
5.02×1.5=7.53(t)
答:这堆沙子大约重7.53吨。
1. 一个圆锥形的零件,底面积是19cm2,高是12cm, 这个零件的体积是多少?
做一做
答:这个零件的体积是76cm? 。
×19 ×12=76(cm )
?
?
2. 一个用钢铸造成的圆锥形铅锤,底面直径是4cm,?高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数)
做一做
(1)铅锤底面积:
3.14 × ? ? ? ? ? ? ?=3.14×4=12.56
(2)铅锤的体积:
×12.56×5≈21
(3)铅锤的质量:
21×7.8≈163(g)
答:这个铅锤大约重163克 。
判断:
1. 圆柱体的体积一定比圆锥体的体积大( ? ? ? )
2. 圆锥的体积等于和它等底等高的圆柱体积的_x0010_ 。 ( ? ? ?)
3. 正方体、长方体、圆锥体的体积都等于底面积×高。 ( ? ? ?)
4. 等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那
么圆锥的体积是9立方米( ? ? ? )
基础练习
2、只列式不计算:
求下面各圆锥的体积 .
基础练习
①底面面积是7.8平方米,高是1.8米。
列式:___________________
②底面半径是4厘米,高是21厘米。
③底面直径是6分米,高是6分米。
列式:___________________
列式:___________________
基础练习
填表:
已 知 条 件
体积
圆锥底面积15平方厘米,高8厘米
圆锥底面半径3分米,高5分米
圆锥底面直径4米,高6米
40立方厘米
47.1立方分米
25.12立方米
1、一个近似于圆锥的沙堆,测得底面直径是4米,高是1.5米。每立方米沙约重1.5吨,这堆沙约重多少吨?
提高练习
答:这堆沙约重9.42吨。
2.有一座圆锥形帐篷,底面直径约5m,高约3.6m。??
(1)它的占地面积约是多少平方米???
(2) 它内部的空间约是多少立方米?
提高练习
3.一个圆柱形橡皮泥,底面积是12cm ,高是5cm。??
(1)如果把它捏成同样底面大小的圆锥,这个圆锥的高是多少?
(2)如果把它捏成同样高的圆锥,这个圆锥的底面积是多少?
提高练习
5×3=15(cm)
2
1.如下图,绿色部分的体积相当于整个物体体积的(? ? ? ?)分之(? ? ? ).
拓展练习
五
二
a
a
a
2、 一个圆锥体,如果高不变,底面积半径 扩大3倍,那么体积将( ? ? ? ? )。
A、扩大3倍 ? ? ? ? ?B、扩大9倍 ? ? ? ? ? ? ?C、扩大6倍
拓展练习
B
3、如图,三角形以AB为轴旋转后所得到的仿锤体的体积是多少?
拓展练习
(3.14×5×5×20+3.14×5×5×10)=785(立方厘米)
下边沙子体积是上边沙子体积的几倍?
拓展练习
下边沙子体积是上边
沙子体积的7倍。
3厘米
3厘米
4. 填空
练习六
(1)一个圆柱的体积是75.36m?,与它等底等高的圆锥的体积是( ? ? ? ? ? )m?。
25.12
(2)一个圆锥的体积是141.3m?,与它等底等高的圆柱的体积是( ? ? ? ? ? )m?。
423.9
5、判断下面的说法是不是正确。
练习六
(1)圆锥的体积等于圆柱体积的? ? ?。( ? ?)
(2)圆柱的体积大于与它等底等高的圆锥的体积。(? ? )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。(? ? )
6、一个圆锥的底面周长是31.4厘米,高是9厘米,它的体积
是多少?
练习六
半径:31.4÷3.14÷2=5(厘米)
体积:? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 235.5(立方厘米)
答:它的体积是235.5立方厘米。
7、一堆煤成圆锥形,高2m,底面周长为18.84m。这堆煤的
体积大约是多少?已知每立方米的煤越重1.4t,这堆煤大约重
多少吨?(得数保留整数)
练习六
半径:18.84÷3.14÷2=3(米)
体积:? ? ? ? ? ? ? ? ? ? ? ? ? ?=18.84(立方米)
大约重:1.4×18.84=26.376≈26(吨)
答:这堆煤的体积大约是18.84立方米,大约重26吨。
8、小明家去年秋季收获的稻谷堆成了圆锥形,高1m,底面直径2m。
(1)这堆稻谷的体积是多少?(保留两位小数)
(2)如果每立方米的稻谷重650kg,这堆稻谷重多少千克?
(3)小明家有0.25公顷稻田,平均每公顷产稻谷多少千克?
(4)如果每千克稻谷售价2.8元,这些稻谷能卖多少钱?
练习六
≈1.05(立方米)
(2)1.05×650=682.5(千克)
(3)682.5÷0.25=2730(千克)
(4)682.5×2.8=1911(元)
(1)
9. 一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
练习六
想一想,当一个圆柱与一个圆锥的底面积和体积分别相等时,圆锥的高与圆柱的高又是什么关系呢?
4×3=12(dm)
答:圆锥的高是12dm 。
10、一个圆柱与圆锥的体积和高分别相等,已知圆锥的底面积
是28.26平方米,圆柱的底面积是多少?
练习六
在等高等体积的前提下,圆柱底面积是圆锥底面积的三分之一,故而 28.26? ? ? ? ?=9.42(平方米)
11、一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失的情况下所积的深度,称为降水量(通常以毫米为单位)。
测定降水量常用的仪器包括雨量器和量筒.我国气象规定,按
24小时的降水量为标准,降水级别如表.
练习六
级别
降水量
/mm
小雨
中雨
大雨
暴雨
大暴雨
特大暴雨
10以下
10~24.9
25~49.9? ? ?50~99.9
100~199.9
200以上
练习六
某区的土地面积为 ? ? ? ? ? ? ? ? ?,2012年7月23日平均降水量为220mm,改日该地区总降水为多少亿立方米?该区一年绿化
用水 为0.4亿立方米,这些雨水的20%能满足绿化用说吗?
1000平方千米=1000000000(平方米)
220×1000000000=220000000000(立方毫米)=2.2(亿立方米)
2.2×20%=0.44(亿立方米)
0.44>0.4
答:这些雨水的20%能满足绿化用水.
度量棱锥的体积
棱锥的体积
将棱锥放入一个底面相同、高度相等的盒子里。棱锥体占据了
整个盒子体积的几分之几?
这是一个相当困难的问题,同时也是相当古老,其历史可以上
溯到古埃及。
? ? 首先,我们很聪明地注意到,如果连接立方体的中心和它的
八个顶点,那么我们就可以将立方体切分成几个棱锥体。
棱锥的体积
? ? 由于立方体的每一个面都对应着一个棱锥体,所以一共有六
个这样的棱锥体。又由于所有的棱锥体都是相同的,所以每一个
棱锥体的体积都是立方体的六分之一。
? ? 截得这个正方体的的一半,可以发现每一个棱锥体的体积都
是这个长方体体积的三分之一。
? ? 然而这一存在一个问题,那就是我们得到的结论仅仅适用于某些特殊形状的棱锥体(其高度正好是它的底面边长的一半)。而大部分的棱锥体并不能刚好组合成立方体或其他规整的形状,它们不是太尖锐就是太平缓。
棱锥的体积
? ? 这是否意味着我们只能度量某些特殊形状的棱锥体呢?幸运的是,实际上并不是这样!这里关键的一点是,如果对特殊的棱锥体进行适当的拉伸变换,我们就可以得到任何形状的棱锥体。例如,如果你想要一个比较尖锐的棱锥
体,我们就可以在垂直方向上对它进行任何
系数的拉伸变换,直到得到我们想要的高度。
这就是最有意思的事,那就是拉伸变换对棱锥体体积所造成的影响和所装盒子的体积的影响是一样的,两者的体积都扩大了拉伸系数倍。这说明两者的体积之比没有发生变化。既然对特殊形状的棱锥体来说,该比值是三分之一,那么对于任何形状的棱锥体来说,该比值也必然是三分之一。因此我们得到结论:任何棱锥体的体积都是刚好装载它的盒子体积的三分之一,也就是它等底等高柱体体积的三分之一。
棱锥的体积
这些知识将在我们中学的学习中继续学习的。
圆锥的体积
