六年级上册数学课件 圆的周长人教版(50张ppt)
文档属性
| 名称 | 六年级上册数学课件 圆的周长人教版(50张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 00:00:00 | ||
图片预览










文档简介
圆的周长
教学目标
理解圆周率的意义,推导出圆周长的计算公式,并能正确的进行简单的计算。
培养学生的观察、比较、分析、综合及动手操作能力。
结合圆周率的学习,对学生进行爱国主义教育。
教学重点
教学难点
推导并总结出圆周长的计算公式。
深入理解圆周率的意义。
圆的周长
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
分别需要多长的铁皮啊?
同学们,你们有办法解决吗?
车轮滚一圈的长度就是它的周长。
如何测量车轮的周长呢?
围成一个平面图形所有边长的总和叫做这个图形的周长。
绕绳法和滚动法
圆的周长与什么有关呢?
与圆的直径(半径)有关.
直径(半径)越长,圆就越大.
绕绳法和滚动法
探索
圆周长和直径的关系:
测圆的周长
⑴绕线法;
⑵滚动法;
⑶其它
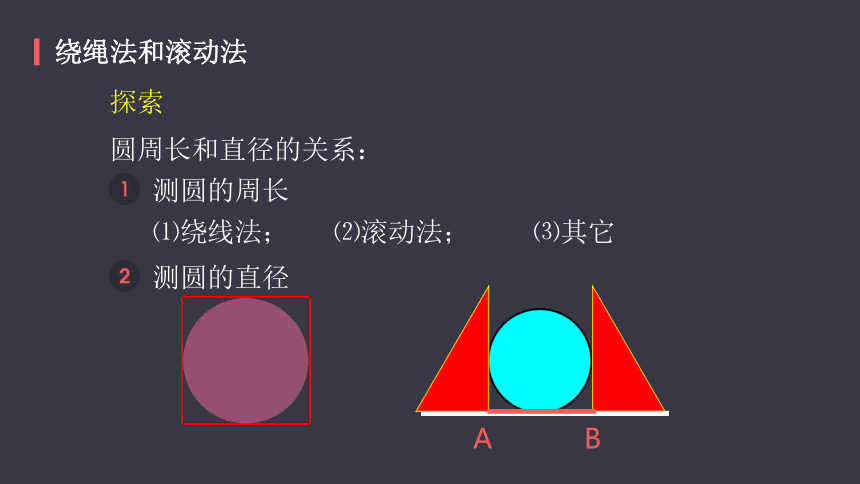
测圆的直径
A
B
绕绳法和滚动法
围成圆的曲线的长就是圆的周长
绕绳法和滚动法
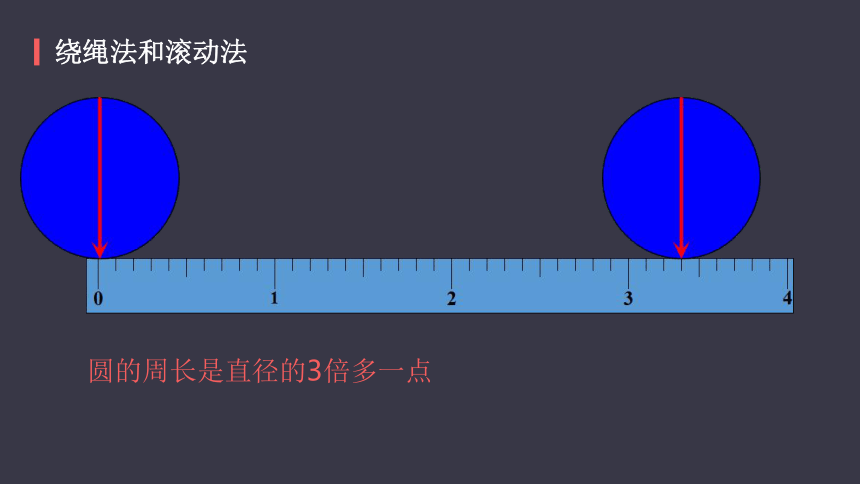
圆的周长是直径的3倍多一点
实验合作
实验活动:
4人一组,准备3个不同大小的圆,分别测量出周长和直径,做一做,再填一填。
物品名称
周长
直径
周长
直径
的比值
(保留两位小数)
实验合作
组
圆的周长
圆的直径
周长
直径
的比值
(保留两位小数)
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
第1组
第2组
第3组
第4组
你发现圆的周长和直径之间有什么关系?
圆周率与周长公式
一个圆的周长总是它的直径的3倍多一些。
? ? ? ?其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π表示。它是一个无限不循环小数,π=3.1415926535……但在实际应用中常常只取它的近似值,例如π≈3.14。
如果用C表示圆的周长,就有:
C =π 或 C=2πr
你知道吗?
你知道吗?
3.141 5926 5358 9793 2384 6264 3383 2795
圆周率
0238 4197 1693 9937 5105 8209 7494 4592
3078 1640 6286 2089 9862 8034 8753 4211
7067 9321 4808 6513 2823 0664 7093 8446
0955 0582 2317 2535 9408 1284 8113 7450...…
例1
这辆自行车后轮轮胎的半径大约是33 cm。
? ? ? ?这辆自行车后轮转一圈,大约可以走多远?小明家离学校1 km,后轮转480圈够吗?
C=2πr
2×3.14×33=207.24(cm)≈ 2.07(m)
1 km=1000 m
1000÷2.07 ≈483(圈)
答:这辆自行车后轮转一圈,大约可以走2.07 m。小明从家到学校,后轮转480圈不够。
做一做
求下面各圆的周长。
2×3.14×3=18.84(cm)
3.14×6=18.84(cm)
2×3.14×5=31.4(cm)
做一做
这个圆桌面的直径是多少?
我用卷尺量得圆桌面的周长是4.71 m。
4.71÷3.14=1.5(m)
答:这个圆桌面的直径是1.5 m。
提高练习
一辆自行车的车轮半径是35厘米,如果车轮平均每分钟转100周,这辆自行车每分钟能行驶_____米.
C=2πr
2×3.14×35=219.8(厘米)=2.198米,
每分钟行驶2.198×100=219.8(米).
提高练习
用一根长20米的绳子围绕一颗树的树干绕了6圈后,还余下1.16m,这棵树的树干的直径大约是____米.
20-1.16=18.84(米),
18.84÷6=3.14(米),
3.14÷3.14=1(米),
所以这棵树的直径是1米.
提高练习
汽车的轮胎外直径是1米,每分钟转335周,如果通过一座长4288米的大桥,大约需要____分钟(保留整数).
C=πd
3.14×1=3.14(米),
3.14×335=1051.9(米),
4288÷1051.9≈4(分),
所以大约需要4分钟.
拓展练习
一个直径是15米的半圆形花园,要在花园的周围围上栅栏,至少需要____米的栅栏.
15×3.14÷2+15=38.55(米),
所以至少需要38.55米的栅栏.
拓展练习
如图所示,有几个大小不一样的圆,圆心同在线段AB上。如果AB长1m,那么这几个圆的周长之和是_________m。
由于这几个圆的心在同一条直线上长,且这几个圆的直径之和等于1,所以这些圆的周长之和等于直径为1米的圆的周长,周长之和为3.14×1=3.14米.
拓展练习
伊丽莎白塔(旧称大本钟)——伦敦市的标志性建筑物。钟盘上时针的长度是2.75m,一昼夜大本钟时针的针尖走过的路程是____米.
C=2πr
2×3.14×2.75=17.27(米),
所以时针的尖端一昼夜所走的距离是17.27×2=34.54(米).
练习
一个圆形喷水池的半径是5m,它的周长是多少米?
2×3.14×3=
31.4(cm)
答:它的周长是31.4cm。
练习
在一个圆形亭子里,小丽沿着直径从一端走12步到达另一端,每步长大约是55cm,这个圆的周长大约是多少?
3.14x(55x12)=
2072.4cm=20.74m
2072.4(cm)
答:这个圆的周长大约是20.74m。
练习
小红量的一个古代建筑中的大红圆柱的周长是3.77m。这个圆柱的直径是多少米?(得数保留一位小数。)
3.77÷3.14≈
1.2(m)
答:这个圆柱的直径是1.2m。
练习
一只挂钟的分针长20co,经过30分钟后,分针的尖端所走过的路程是多少厘米?经过45分钟呢?
答:经过30分钟分针尖端走过62.8cm,经过45分尖端走过94.2cm。
练习
一个圆形牛栏的半径是15米,要用多长的粗铁丝才能把牛栏围上3圈?(接头处忽略不计)如果每隔两米达打一根木桩,大约要打多少根木桩?
2x3.14x15x3=
282.6(米)
2x3.14x15÷2≈
47(根)
答:要用282.6米长的粗铁丝才能把牛栏围上3圈。大约要打47根木桩.
练习
杂技演员表演独轮车走钢丝,车轮的直径为40cm,要骑过50.24m唱的钢丝,车轮大约要转动多少周?
3.14x40=
125.6(cm)
125.6cm=1.256m
50.24÷1.256=
40(周)
答:车轮大约要转动40周。
练习
看图填空(单位:cm)
正方形的周长是(? ? ? )cm
圆的周长是(? ? ? ? ? )cm
其中一个圆的周长是(? ? ? ? ? )cm
长方形的周长是(? ? ? )cm
16
12.56
9.42
21
练习
一个周长为100cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是多少厘米?
答:这个圆的半径是12.5m。
练习
李明家一扇门上要装上如右图所示的装饰木条,需要木条多少米?
50x4+3.14x50÷2=
278.5(cm)
278.5cm=2.785m
答:需要木条2.785m
练习
下面图形的周长是多少厘米?你是怎样算的?
2x3.15x5÷2+3.14x5=
31.4(m)
练习
把圆柱形物体分别捆成如下图(从底面方向看)的形状,如果接头处不计,每组至少需要多长的绳子?你发现了什么?
第一幅图:
7x2+3.14x7=35.98(m)
第二幅图:
第三幅图:
7x4+3.14x7=49.98(m)
7x8+3.14x7=77.98(m)
圆周率的历史
数学阅读
圆周率的历史
圆周率的历史
? ? ? ?轮子是古代的重要发明。由于轮子的普遍应用,人们很容易想到这样一个问题:一个轮子滚一圈可以滚多远?那么滚的距离与轮子的直径之间有什么关系呢?
圆周率的历史
? ? ? ?最早的解决方案是测量。当许多人多次测量之后,人们发现了圆的周长总是其直径的倍多。在我国,现存有关圆周率的最早记载是2000多年前的《周髀算经》。
? ? ? ?用测量的方法计算圆周率,圆周率的精确程度取决于测量的精确度,而有许多实际困难限制了测量的精度。
圆周率的历史
? ? ? ?在我国,首先是由魏晋时期杰出的数学家刘徽得出了较精确的圆周率的值。他采用“割圆术”一直算到圆内接正92边形, 得到圆周率的近似值是3.14。刘徽的方法是用圆内接正多边形从一个方向逐步逼近圆。
刘徽
圆周率的历史
? ? ? ?公元前3世纪,古希腊数学家阿基米德发现:当正多边形的边数增加时,它的形状就越来越接近圆。这一发现提供了计算圆周率的新途径,阿基米德用圆内接正多边形和圆外切正多边形从两个方向上同时逐步逼近圆,获得了圆周率的值介于? ? ?和? ? ?之间。
圆周率的历史
? ? ? ?恐怕大家更熟悉的是祖冲之所做的贡献吧!1500多年前,我国南北朝时期著名的数学家祖冲之算出 的值在3.1415926和3.1415927之间,并且得到了 的两个分数形式的近似值:约率为? ? ? ?,密率为? ? ? ?。
祖冲之
圆周率的历史
? ? ? ?这一成就在世界上领先了约1000年。祖冲之取得的这一非凡成果,正是基于刘徽割圆术的继承与发展。他自己是否还使用了其他的巧妙办法呢?这已经不得而知。祖冲之的这一研究成果享有世界声誉。巴黎“发现宫”科学博物馆的墙壁上介绍了祖冲之求得的圆周率,莫斯科大学礼堂的走廊上镶嵌有祖冲之的大理石像,月球上有以祖冲之命名的环形山……
祖冲之
圆周率的历史
利用“投针试验”求圆周率
? ? ? ?历史上,法国数学家布丰最早设计了投针试验,并于1777年给出了针于平行线相交的概率的计算公式P=2l/πa,由于它与π有关,于是人们想到利用投针试验来估计π的值。
圆周率的历史
? ? ? ?用正方边形逼近圆,计算量很大,再向前推进,必须在方法上有所突破。随着数学的不断发展,人类开始摆脱求正多边形周长的繁难计算,求圆周率的方法也日新月异。近代以来,很多数学家都进行了深入的研究,并取得了不同程度的成果。
圆周率的历史
? ? ? ?电子计算机的出现带来了计算方面的革命, 的小数点后面的精确数字越来越多。2000年,某研究小组使用最先进的超级计算机,将圆周率计算到了小数点后12411亿位。
? ? ? ?现在计算? ? 的值已经被人们用来测试或检验超级计算机的各项性能,特别是用来测试运算速度与计算过程的稳定性。
π
π
圆周率的历史
圆周率的计算历史
时间
前2000
前1200
前500?
前250??
前263
480?
1429?
古埃及
中国
圣经
Archimedes?
刘徽
祖冲之
Al-Kashi??
1
1
1
3
5
7
14
纪录创造者?
小数点后位数
…
…
…
圆周率的历史
圆周率的探索者
教学目标
理解圆周率的意义,推导出圆周长的计算公式,并能正确的进行简单的计算。
培养学生的观察、比较、分析、综合及动手操作能力。
结合圆周率的学习,对学生进行爱国主义教育。
教学重点
教学难点
推导并总结出圆周长的计算公式。
深入理解圆周率的意义。
圆的周长
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
分别需要多长的铁皮啊?
同学们,你们有办法解决吗?
车轮滚一圈的长度就是它的周长。
如何测量车轮的周长呢?
围成一个平面图形所有边长的总和叫做这个图形的周长。
绕绳法和滚动法
圆的周长与什么有关呢?
与圆的直径(半径)有关.
直径(半径)越长,圆就越大.
绕绳法和滚动法
探索
圆周长和直径的关系:
测圆的周长
⑴绕线法;
⑵滚动法;
⑶其它
测圆的直径
A
B
绕绳法和滚动法
围成圆的曲线的长就是圆的周长
绕绳法和滚动法
圆的周长是直径的3倍多一点
实验合作
实验活动:
4人一组,准备3个不同大小的圆,分别测量出周长和直径,做一做,再填一填。
物品名称
周长
直径
周长
直径
的比值
(保留两位小数)
实验合作
组
圆的周长
圆的直径
周长
直径
的比值
(保留两位小数)
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
cm
第1组
第2组
第3组
第4组
你发现圆的周长和直径之间有什么关系?
圆周率与周长公式
一个圆的周长总是它的直径的3倍多一些。
? ? ? ?其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π表示。它是一个无限不循环小数,π=3.1415926535……但在实际应用中常常只取它的近似值,例如π≈3.14。
如果用C表示圆的周长,就有:
C =π 或 C=2πr
你知道吗?
你知道吗?
3.141 5926 5358 9793 2384 6264 3383 2795
圆周率
0238 4197 1693 9937 5105 8209 7494 4592
3078 1640 6286 2089 9862 8034 8753 4211
7067 9321 4808 6513 2823 0664 7093 8446
0955 0582 2317 2535 9408 1284 8113 7450...…
例1
这辆自行车后轮轮胎的半径大约是33 cm。
? ? ? ?这辆自行车后轮转一圈,大约可以走多远?小明家离学校1 km,后轮转480圈够吗?
C=2πr
2×3.14×33=207.24(cm)≈ 2.07(m)
1 km=1000 m
1000÷2.07 ≈483(圈)
答:这辆自行车后轮转一圈,大约可以走2.07 m。小明从家到学校,后轮转480圈不够。
做一做
求下面各圆的周长。
2×3.14×3=18.84(cm)
3.14×6=18.84(cm)
2×3.14×5=31.4(cm)
做一做
这个圆桌面的直径是多少?
我用卷尺量得圆桌面的周长是4.71 m。
4.71÷3.14=1.5(m)
答:这个圆桌面的直径是1.5 m。
提高练习
一辆自行车的车轮半径是35厘米,如果车轮平均每分钟转100周,这辆自行车每分钟能行驶_____米.
C=2πr
2×3.14×35=219.8(厘米)=2.198米,
每分钟行驶2.198×100=219.8(米).
提高练习
用一根长20米的绳子围绕一颗树的树干绕了6圈后,还余下1.16m,这棵树的树干的直径大约是____米.
20-1.16=18.84(米),
18.84÷6=3.14(米),
3.14÷3.14=1(米),
所以这棵树的直径是1米.
提高练习
汽车的轮胎外直径是1米,每分钟转335周,如果通过一座长4288米的大桥,大约需要____分钟(保留整数).
C=πd
3.14×1=3.14(米),
3.14×335=1051.9(米),
4288÷1051.9≈4(分),
所以大约需要4分钟.
拓展练习
一个直径是15米的半圆形花园,要在花园的周围围上栅栏,至少需要____米的栅栏.
15×3.14÷2+15=38.55(米),
所以至少需要38.55米的栅栏.
拓展练习
如图所示,有几个大小不一样的圆,圆心同在线段AB上。如果AB长1m,那么这几个圆的周长之和是_________m。
由于这几个圆的心在同一条直线上长,且这几个圆的直径之和等于1,所以这些圆的周长之和等于直径为1米的圆的周长,周长之和为3.14×1=3.14米.
拓展练习
伊丽莎白塔(旧称大本钟)——伦敦市的标志性建筑物。钟盘上时针的长度是2.75m,一昼夜大本钟时针的针尖走过的路程是____米.
C=2πr
2×3.14×2.75=17.27(米),
所以时针的尖端一昼夜所走的距离是17.27×2=34.54(米).
练习
一个圆形喷水池的半径是5m,它的周长是多少米?
2×3.14×3=
31.4(cm)
答:它的周长是31.4cm。
练习
在一个圆形亭子里,小丽沿着直径从一端走12步到达另一端,每步长大约是55cm,这个圆的周长大约是多少?
3.14x(55x12)=
2072.4cm=20.74m
2072.4(cm)
答:这个圆的周长大约是20.74m。
练习
小红量的一个古代建筑中的大红圆柱的周长是3.77m。这个圆柱的直径是多少米?(得数保留一位小数。)
3.77÷3.14≈
1.2(m)
答:这个圆柱的直径是1.2m。
练习
一只挂钟的分针长20co,经过30分钟后,分针的尖端所走过的路程是多少厘米?经过45分钟呢?
答:经过30分钟分针尖端走过62.8cm,经过45分尖端走过94.2cm。
练习
一个圆形牛栏的半径是15米,要用多长的粗铁丝才能把牛栏围上3圈?(接头处忽略不计)如果每隔两米达打一根木桩,大约要打多少根木桩?
2x3.14x15x3=
282.6(米)
2x3.14x15÷2≈
47(根)
答:要用282.6米长的粗铁丝才能把牛栏围上3圈。大约要打47根木桩.
练习
杂技演员表演独轮车走钢丝,车轮的直径为40cm,要骑过50.24m唱的钢丝,车轮大约要转动多少周?
3.14x40=
125.6(cm)
125.6cm=1.256m
50.24÷1.256=
40(周)
答:车轮大约要转动40周。
练习
看图填空(单位:cm)
正方形的周长是(? ? ? )cm
圆的周长是(? ? ? ? ? )cm
其中一个圆的周长是(? ? ? ? ? )cm
长方形的周长是(? ? ? )cm
16
12.56
9.42
21
练习
一个周长为100cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是多少厘米?
答:这个圆的半径是12.5m。
练习
李明家一扇门上要装上如右图所示的装饰木条,需要木条多少米?
50x4+3.14x50÷2=
278.5(cm)
278.5cm=2.785m
答:需要木条2.785m
练习
下面图形的周长是多少厘米?你是怎样算的?
2x3.15x5÷2+3.14x5=
31.4(m)
练习
把圆柱形物体分别捆成如下图(从底面方向看)的形状,如果接头处不计,每组至少需要多长的绳子?你发现了什么?
第一幅图:
7x2+3.14x7=35.98(m)
第二幅图:
第三幅图:
7x4+3.14x7=49.98(m)
7x8+3.14x7=77.98(m)
圆周率的历史
数学阅读
圆周率的历史
圆周率的历史
? ? ? ?轮子是古代的重要发明。由于轮子的普遍应用,人们很容易想到这样一个问题:一个轮子滚一圈可以滚多远?那么滚的距离与轮子的直径之间有什么关系呢?
圆周率的历史
? ? ? ?最早的解决方案是测量。当许多人多次测量之后,人们发现了圆的周长总是其直径的倍多。在我国,现存有关圆周率的最早记载是2000多年前的《周髀算经》。
? ? ? ?用测量的方法计算圆周率,圆周率的精确程度取决于测量的精确度,而有许多实际困难限制了测量的精度。
圆周率的历史
? ? ? ?在我国,首先是由魏晋时期杰出的数学家刘徽得出了较精确的圆周率的值。他采用“割圆术”一直算到圆内接正92边形, 得到圆周率的近似值是3.14。刘徽的方法是用圆内接正多边形从一个方向逐步逼近圆。
刘徽
圆周率的历史
? ? ? ?公元前3世纪,古希腊数学家阿基米德发现:当正多边形的边数增加时,它的形状就越来越接近圆。这一发现提供了计算圆周率的新途径,阿基米德用圆内接正多边形和圆外切正多边形从两个方向上同时逐步逼近圆,获得了圆周率的值介于? ? ?和? ? ?之间。
圆周率的历史
? ? ? ?恐怕大家更熟悉的是祖冲之所做的贡献吧!1500多年前,我国南北朝时期著名的数学家祖冲之算出 的值在3.1415926和3.1415927之间,并且得到了 的两个分数形式的近似值:约率为? ? ? ?,密率为? ? ? ?。
祖冲之
圆周率的历史
? ? ? ?这一成就在世界上领先了约1000年。祖冲之取得的这一非凡成果,正是基于刘徽割圆术的继承与发展。他自己是否还使用了其他的巧妙办法呢?这已经不得而知。祖冲之的这一研究成果享有世界声誉。巴黎“发现宫”科学博物馆的墙壁上介绍了祖冲之求得的圆周率,莫斯科大学礼堂的走廊上镶嵌有祖冲之的大理石像,月球上有以祖冲之命名的环形山……
祖冲之
圆周率的历史
利用“投针试验”求圆周率
? ? ? ?历史上,法国数学家布丰最早设计了投针试验,并于1777年给出了针于平行线相交的概率的计算公式P=2l/πa,由于它与π有关,于是人们想到利用投针试验来估计π的值。
圆周率的历史
? ? ? ?用正方边形逼近圆,计算量很大,再向前推进,必须在方法上有所突破。随着数学的不断发展,人类开始摆脱求正多边形周长的繁难计算,求圆周率的方法也日新月异。近代以来,很多数学家都进行了深入的研究,并取得了不同程度的成果。
圆周率的历史
? ? ? ?电子计算机的出现带来了计算方面的革命, 的小数点后面的精确数字越来越多。2000年,某研究小组使用最先进的超级计算机,将圆周率计算到了小数点后12411亿位。
? ? ? ?现在计算? ? 的值已经被人们用来测试或检验超级计算机的各项性能,特别是用来测试运算速度与计算过程的稳定性。
π
π
圆周率的历史
圆周率的计算历史
时间
前2000
前1200
前500?
前250??
前263
480?
1429?
古埃及
中国
圣经
Archimedes?
刘徽
祖冲之
Al-Kashi??
1
1
1
3
5
7
14
纪录创造者?
小数点后位数
…
…
…
圆周率的历史
圆周率的探索者
