六年级上册数学课件-扇形 人教版(31张ppt)
文档属性
| 名称 | 六年级上册数学课件-扇形 人教版(31张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 17:40:56 | ||
图片预览









文档简介
扇形
教学目标
理解和建立扇形概念,认识圆心角和弧。
在认识圆心角的过程中,培养学生的观察能力。
学会欣赏数学之美,热爱生活。?
教学重点
教学难点
建立扇形的概念。
理解圆心角的大小与扇形大小的关系。
你能指出这个圆的圆心、半径和直径吗?
知识引入
O
d
r
知识引入
怎样计算圆的面积?
r
d
C
×
×
2
3.14
÷
÷
知识引入
一个底面是圆形的蒙古包,沿地面量得周长25.12 m,它的占地面积是多少平方米?
25.12÷3.14=8(m)
8÷2=4(m)
3.14×4?=50.24(m?)
答:它的占地面积是50.24 m?。
扇形
扇形进阶
扇形的认识
什么是扇形?
它们的外形都是扇形的。
这些物体的外形有什么相同的地方?
扇形的认识
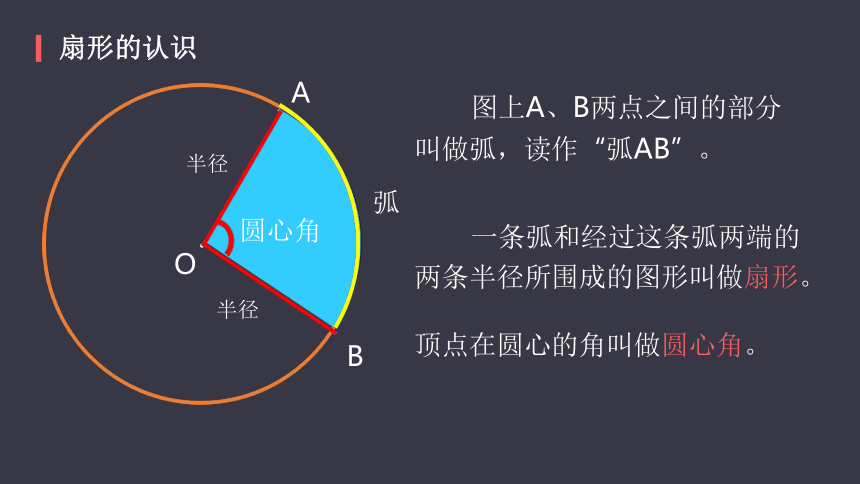
? ? ? ?图上A、B两点之间的部分
叫做弧,读作“弧AB”。
? ? ? ?一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
O
A
B
弧
半径
半径
圆心角
扇形的认识
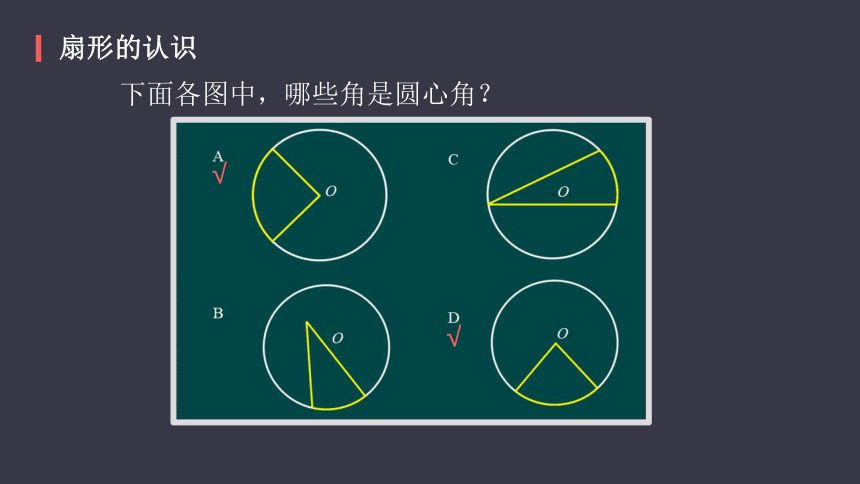
下面各图中,哪些角是圆心角?
√
√
扇形的认识
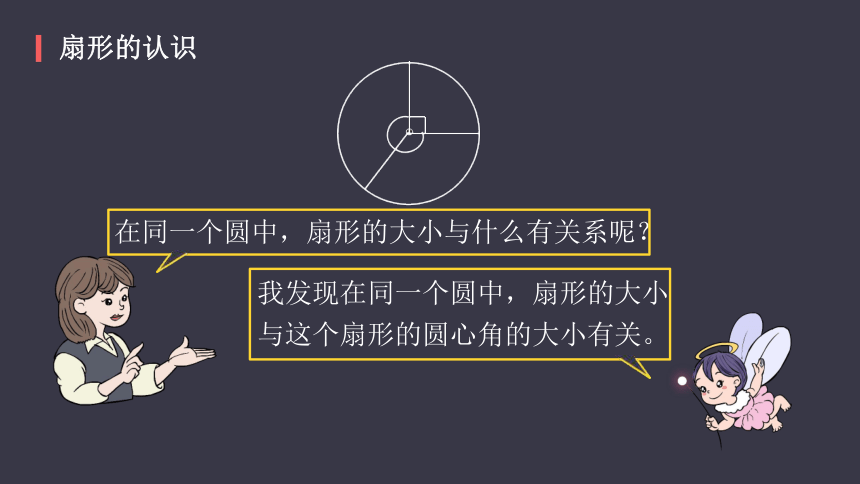
在同一个圆中,扇形的大小与什么有关系呢?
我发现在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
扇形的认识
以半圆为弧的扇形的圆心角是多少度?以? ? 圆为弧的扇形呢?
以半圆为弧的扇形的圆心角是180°。
以? ? 圆为弧的扇形的圆心角是90°。
180°
90°
生活中的扇形
生活中的扇形
练习
指出下列物体中的扇形。
参考答案
练习
下面图形中哪些角是圆心角?在( )里画“√”。
√
√
练习
画一个半径是2cm的圆,再在圆中画一个圆心角是100°的扇形。
练习
你在生活中见过下面这些图案吗?
像下面这样一个圆环被截得的部分叫做扇环。你能求出下面各扇环的面积吗?
答:
左图:3.14×[5?-(5-2)?]× =12.56(dm?)
右图:3.14×[4?-(4-1)?]× ×2=10.99(dm?)
提高练习
把一个圆平均分成4个扇形,每个扇形的周长和这个圆的直径的比是(? ? )
A.
B.
B
提高练习
把一张圆纸片三次对折后,每个小扇形的圆心角是(? ? ?)°。
45
提高练习
求图中等边三角形中阴影部分的面积。(单位:dm)
3.14×4?×? ? ? ?=25.12(dm?)
拓展练习
图中三个圆的周长都是25.12厘米,求阴影部分面积的总和。
扇形部分圆心角之和是:540-120-150=270(度)
扇形半径:25.12÷3.14÷2=4(cm)
阴影部分的面积总和:
3.14×4?×? ? ?=37.68(cm?)
拓展练习
草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见下图).这只羊能够活动的范围有____平方米.
所以这只羊能够活动的范围有2512平方米.
拓展练习
用铁丝将3根直径是1分米的圆柱捆绑一周,如下图。求铁丝的长度。(接头忽略不计)。
铁丝的长度:1×3+3.14×1=6.14(dm)
李冶与《测圆海镜》
? ? ? ?李冶(1192-1279)是中国古代数学家,字仁卿,号敬斋,真定府栾城县(今河北省栾城县)人,宋元数学四大家之一。
《测圆海镜》(1248)
《益古演段》(1259)
李冶与《测圆海镜》
? ? ? ?《测圆海镜》由中国金、元时期数学家李冶所著,成书于1248年。全书共有12卷,170问。这是中国古代论述容圆的一部专著,也是天元术的代表作。
? ? ? ?《测圆海镜》所讨论的问题大都是已知勾股形而求其内切圆、旁切圆等的直径一类的问题。勾股形的解法是古代传统数学的重要内容之一。?
李冶与《测圆海镜》
? ? ? ?此外,在中国古代数学的发展中,天元术起着重要的作用。在《测圆海镜》问世之前,我国虽有文字代表未知数用以布列方程和多项式的工作,但是没有留下很有系统的记载。李冶在《测圆海镜》中系统而概括地总结了天元术,使文词代数开始演变成符号代数。
? ? ? ?所谓天元术,就是设“天元一”为未知数,根据问题的已知条件,列出两个相等的多项式,经相减后得出一个高次方程式,称为天元开方式,这与现代设x为未知数列方程一样。欧洲的数学家,只有到了16世纪以后才完全作到这一点。《测圆海镜》全书170 题,基本上都是(依据《识别杂记》)列出天元式,求出勾股容圆问题的解。
李冶与《测圆海镜》
天元术
《测圆海镜》(1248)
天元术(一元高次方程)
列方程法
“立天元一为某某”
“设x为某某”
李冶与《测圆海镜》
李冶的天元术
李冶与《测圆海镜》
? ? ? ?《测圆海镜》数学上的成就有三点:“天元术”,即列方程解决问题的一种“机械化”程序,相当于现代设x为未知数列方程的方法,这是一项具有世界意义的创举;勾股形解法,把传统的勾股形研究推进到一个新的层次;数学抽象化的新起点:此书虽然形式上仍采用问题集的表述方式,但问题显然已不是从实际生活中得来的,而是出于数学研究的需要产生的,只是出于传统,披上了“实用”的外衣,这对中国古代数学无疑是一种重要的突破和补充,就内容看,给出了一些专门的概念和公式(“识别杂记”),采用了演绎推理的方法等,在中国数学思想发展中占有重要的地位。
教学目标
理解和建立扇形概念,认识圆心角和弧。
在认识圆心角的过程中,培养学生的观察能力。
学会欣赏数学之美,热爱生活。?
教学重点
教学难点
建立扇形的概念。
理解圆心角的大小与扇形大小的关系。
你能指出这个圆的圆心、半径和直径吗?
知识引入
O
d
r
知识引入
怎样计算圆的面积?
r
d
C
×
×
2
3.14
÷
÷
知识引入
一个底面是圆形的蒙古包,沿地面量得周长25.12 m,它的占地面积是多少平方米?
25.12÷3.14=8(m)
8÷2=4(m)
3.14×4?=50.24(m?)
答:它的占地面积是50.24 m?。
扇形
扇形进阶
扇形的认识
什么是扇形?
它们的外形都是扇形的。
这些物体的外形有什么相同的地方?
扇形的认识
? ? ? ?图上A、B两点之间的部分
叫做弧,读作“弧AB”。
? ? ? ?一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
O
A
B
弧
半径
半径
圆心角
扇形的认识
下面各图中,哪些角是圆心角?
√
√
扇形的认识
在同一个圆中,扇形的大小与什么有关系呢?
我发现在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
扇形的认识
以半圆为弧的扇形的圆心角是多少度?以? ? 圆为弧的扇形呢?
以半圆为弧的扇形的圆心角是180°。
以? ? 圆为弧的扇形的圆心角是90°。
180°
90°
生活中的扇形
生活中的扇形
练习
指出下列物体中的扇形。
参考答案
练习
下面图形中哪些角是圆心角?在( )里画“√”。
√
√
练习
画一个半径是2cm的圆,再在圆中画一个圆心角是100°的扇形。
练习
你在生活中见过下面这些图案吗?
像下面这样一个圆环被截得的部分叫做扇环。你能求出下面各扇环的面积吗?
答:
左图:3.14×[5?-(5-2)?]× =12.56(dm?)
右图:3.14×[4?-(4-1)?]× ×2=10.99(dm?)
提高练习
把一个圆平均分成4个扇形,每个扇形的周长和这个圆的直径的比是(? ? )
A.
B.
B
提高练习
把一张圆纸片三次对折后,每个小扇形的圆心角是(? ? ?)°。
45
提高练习
求图中等边三角形中阴影部分的面积。(单位:dm)
3.14×4?×? ? ? ?=25.12(dm?)
拓展练习
图中三个圆的周长都是25.12厘米,求阴影部分面积的总和。
扇形部分圆心角之和是:540-120-150=270(度)
扇形半径:25.12÷3.14÷2=4(cm)
阴影部分的面积总和:
3.14×4?×? ? ?=37.68(cm?)
拓展练习
草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见下图).这只羊能够活动的范围有____平方米.
所以这只羊能够活动的范围有2512平方米.
拓展练习
用铁丝将3根直径是1分米的圆柱捆绑一周,如下图。求铁丝的长度。(接头忽略不计)。
铁丝的长度:1×3+3.14×1=6.14(dm)
李冶与《测圆海镜》
? ? ? ?李冶(1192-1279)是中国古代数学家,字仁卿,号敬斋,真定府栾城县(今河北省栾城县)人,宋元数学四大家之一。
《测圆海镜》(1248)
《益古演段》(1259)
李冶与《测圆海镜》
? ? ? ?《测圆海镜》由中国金、元时期数学家李冶所著,成书于1248年。全书共有12卷,170问。这是中国古代论述容圆的一部专著,也是天元术的代表作。
? ? ? ?《测圆海镜》所讨论的问题大都是已知勾股形而求其内切圆、旁切圆等的直径一类的问题。勾股形的解法是古代传统数学的重要内容之一。?
李冶与《测圆海镜》
? ? ? ?此外,在中国古代数学的发展中,天元术起着重要的作用。在《测圆海镜》问世之前,我国虽有文字代表未知数用以布列方程和多项式的工作,但是没有留下很有系统的记载。李冶在《测圆海镜》中系统而概括地总结了天元术,使文词代数开始演变成符号代数。
? ? ? ?所谓天元术,就是设“天元一”为未知数,根据问题的已知条件,列出两个相等的多项式,经相减后得出一个高次方程式,称为天元开方式,这与现代设x为未知数列方程一样。欧洲的数学家,只有到了16世纪以后才完全作到这一点。《测圆海镜》全书170 题,基本上都是(依据《识别杂记》)列出天元式,求出勾股容圆问题的解。
李冶与《测圆海镜》
天元术
《测圆海镜》(1248)
天元术(一元高次方程)
列方程法
“立天元一为某某”
“设x为某某”
李冶与《测圆海镜》
李冶的天元术
李冶与《测圆海镜》
? ? ? ?《测圆海镜》数学上的成就有三点:“天元术”,即列方程解决问题的一种“机械化”程序,相当于现代设x为未知数列方程的方法,这是一项具有世界意义的创举;勾股形解法,把传统的勾股形研究推进到一个新的层次;数学抽象化的新起点:此书虽然形式上仍采用问题集的表述方式,但问题显然已不是从实际生活中得来的,而是出于数学研究的需要产生的,只是出于传统,披上了“实用”的外衣,这对中国古代数学无疑是一种重要的突破和补充,就内容看,给出了一些专门的概念和公式(“识别杂记”),采用了演绎推理的方法等,在中国数学思想发展中占有重要的地位。
