六年级上册数学课件-按比分配 人教版(37张ppt)
文档属性
| 名称 | 六年级上册数学课件-按比分配 人教版(37张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 17:43:30 | ||
图片预览










文档简介
比
例2 按比分配
教学目标
在自主探索中理解按比例分配的意义.
掌握按比例分配问题的结构特点以及解题方法,能正确解答按比例分配问题.
培养优化意识和平合作精神.
教学重点
教学难点
理解按一定比例来分配一个数量的意义,根据题中所给的比,掌握各部分量占总数量的几分之几,能熟练地求出各部分量.
理解并掌握按比分配应用题的数量关系.
年级班男生人数与女生人数的比是4 ∶5.
提示:可以把男生人数看作( ? ?)份,女生人数有( ? ? )份. 全班共有( ? ? )份.
男生人数是女生人数的( ? ? ),
女生人数是男生人数的( ? ? ?),
男生人数是全班总人数的( ? ? ),
女生人数是全班总人数的( ? ? ).
4
5
9
爸爸发送了一个100元的微信红包,小明抢到60元妈妈抢到40元。
小明抢到的金额与妈妈抢到的金额的比是( ? ? ? ? )。?
两个人互相说一说这个比的意义。?
3 : 2
按比分配
例2 这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液.
问题: (1)什么是稀释液?什么是浓缩液?
(2)浓度是1:2的稀释液怎么配制呢?
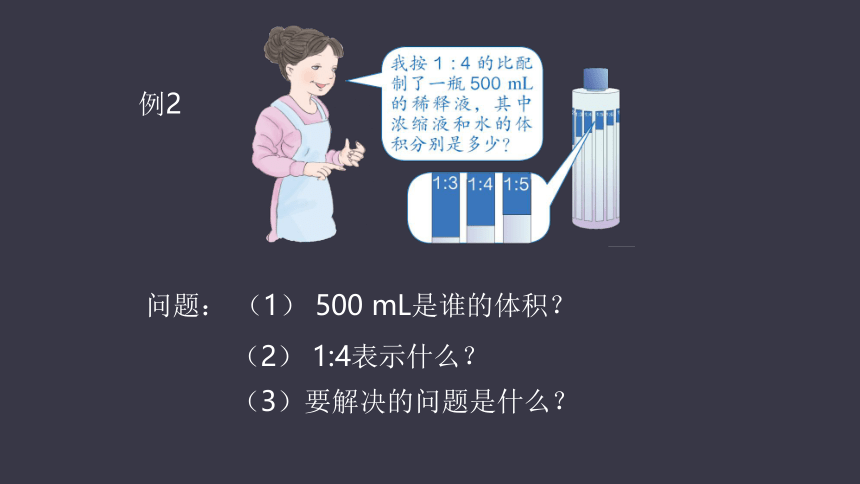
例2
问题: (1) 500 mL是谁的体积?
(2) 1:4表示什么?
(3)要解决的问题是什么?
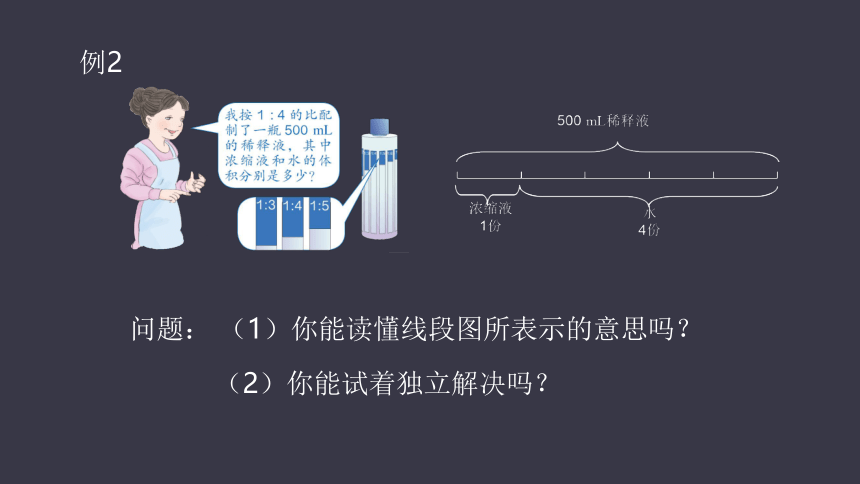
例2
问题: (1)你能读懂线段图所表示的意思吗?
(2)你能试着独立解决吗?
例2
方法1:
① 总份数:4+1=5
② 每份是:4÷1=5(mL)
③ 浓缩液有:100×1=100(mL)
④ 水有:100×4=400(mL)
问题: (3)你知道两种解法中每一步求的是什么吗?
(4)两种解法有什么联系和区别?
方法2:
① 总份数:4+1=5
例2
方法1:
① 总份数:4+1=5
② 每份是:4÷1=5(mL)
③ 浓缩液有:100×1=100(mL)
④ 水有:100×4=400(mL)
方法2:
① 总份数:4+1=5
问题:如何检验解答是否正确呢?
(1)浓缩液+水=500 mL ? ?(2)浓缩液︰水=1:4
在日常生活和工农业生产中,常常需要把一个数量按照一定的比来进行分配,这种分配方法通常叫做按比分配.
“按比分配”解决问题
特点:
已知两个数(三个数)的和与这两个数(三个数)的比.
求这两个数(三个数)各是多少?
按比分配解决问题一般步骤(份数法)
分什么,有多少?
总数量
怎样分?
( )︰( )或( )︰( )︰( )
求平均分的总份数(前项+后项)
求每份是多少?(总数量÷总份数)
再求出每部分是多少?
按比分配解决问题一般步骤:(分数乘法)
分什么,有多少?
总数量
怎样分?
( )︰( )或( )︰( )︰( )
求平均分的总份数(前项+后项)
求每部分占总数量的几分之几是多少?
用分数乘法求出每部分是多少
转化成
1.某妇产医院上月新生儿303名,男女婴儿人数之比是51:50.
上月新生男、女婴儿各有多少人?
303÷(51+50)=3(人)?
3×51=153(人)?
3×50=150(人)?
答:上月新生男婴儿153人,女婴儿150人.
2.
200÷(1+9)=20(mL)
20×1=20(mL)
20×9=180(mL)
答:需要蜂蜜20mL,水180mL.
3.
一共有多少名游客?多少名救生员?
7+1=8
答:一共有49名游客,7名救生员.
4. 学校把栽70棵树的任务按照六年级三个班的人数分配给各班,一班有46人,二班有44人,三班有50人. 三个班各应栽多少棵数?
答:一班应栽23棵树,二班应栽22棵树, 三班应栽25棵树.
5. 比和除法、分数有什么关系?比的基本性质是什么?请化简下列各比.
24:36
2:3
0.75:1
3:4
5:6
答:比的前项相当于除法中的被除数,分数中的分子;比的后项相当于除法中的除数,分数中的分母;比号相当于除法中的除号,分数中的分数线;比值相当于除法中的商,分数的分值;不同的是:比是指两个量之间的关系;除法是一种运算;分数是一个数。比的基本性质:比的前项和后项同时乘或除以(0除外)相同的数,比值不变,这叫做比的基本性质.
6. 填空.
4
50
0.8
1.25
4
5
9
4
(3)20kg:0.2t的比值是( ? ? ).
7.
三种蔬菜的面积分别是多少平方米?
800-320=480(m?)
答:西红柿的面积是320m?、黄瓜的面积是320m?、茄子的面积是160m?.
8. 请你根据下面的信息,寻找合适的量,写出这些量之间的比.
参考答案?
我和爸爸的年龄比是6:19;?
爸爸和妈妈一年的工资的比是3:2.
9. 某仓库里储存了150t大米、60t面粉和15t杂粮,求这个仓库里储存的大米、面粉和杂粮的比. 并把它化成最简单的整数比.
大米:面粉:杂粮=150t:60t:15t
=150:60:15
=10:4:1
答:这个仓库里储存的大米、面粉和杂粮的比是150:60:15,化成最简整数比是10:4:1.
10. 搅拌混凝土需要水泥、沙子和石子共20t. 三种原料分别需要多少吨?
2+3+5=10
答:需要水泥4t,沙子6t,石子10t.
11. 用120cm的铁丝做成一个长方体的框架. 长、宽、高的比是3:2:1. 这个长方体的长、宽、高分别是多少?
120÷4=30(cm)
3+2+1=6
答:这个长方体的长是15cm,宽是10cm,高是5cm.
1.长方形的周长是10厘米,长与宽的比是4:1,这个长方形的宽是____厘米,长是____厘米.
10÷2×(4+1)=1(厘米),所以这个长方形的宽是1×1=1(厘米),长是1×4=4(厘米).
提高练习
2.做一个长方体的木箱,它的所有棱长之和为112分米,它的长、宽、高之比为6∶5∶3,这个木箱的体积是____立方分米.
112÷4=28(分米),28÷(6+5+3)=2(分米),则长方体的长为2×6=12(分米),宽为2×5=10(分米),高为2×3=6(分米),所以这个木箱的体积是12×10×6=720(立方分米).
提高练习
3.被减数、减数与差的和是80,减数和差的比是3∶5,差是____.
80÷(3+5+8)=5,所以差是5×5=25.
提高练习
1.养殖场里兔子的只数在180~200之间,白兔和黑兔的只数比是9:7,养殖场里白兔比黑兔多____只.
180÷(9+7)=11.25,则兔子的总只数16×12=192(只),所以养殖场里白兔比黑兔多192÷(9+7)×(9-7)=24(只).
拓展练习
2.A、B两种商品的价格比是7:3.如果它们的价格分别上涨70元,那么它们现在的价格比是7:4,A种商品原来的价格是____元.
拓展练习
3.甲、乙两包糖的重量比为4:1.从甲包取出130克放入乙包后,甲、乙两包糖的重量比为7:5.原来甲包有____克糖.
拓展练习
艺术中的黄金比
雕塑高2.04米,从肚脐到脚底高1.26米.
1.26︰2.04≈0.618
爱与美之神“维纳斯”,表现出最美的人.
a
b
断臂女神维纳斯
项目
女神维纳斯
艺术中的黄金比
著名画家达?芬奇的蒙娜丽莎构图就完美的体现了黄金比在油画艺术上的应用. 通过上面三幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都体现了黄金比,使得这幅油画看起来是那么的和谐完美.?
“检阅”西方的一一幅优美油画,它的画杠结构比例也正是0.618的比值.
艺术中的黄金比
音乐中的黄金比
音乐家发现,二胡演奏中,“千金”分弦的比符合0.618∶1时,奏出来的音调最和谐、最悦耳.
肖邦的《降D大调夜曲》全曲不计前奏共76小节,理论计算黄金分割点应在46小节,而再现部恰恰位于46小节,是全曲力度最强的高潮所在,真是巧夺天工!
例2 按比分配
教学目标
在自主探索中理解按比例分配的意义.
掌握按比例分配问题的结构特点以及解题方法,能正确解答按比例分配问题.
培养优化意识和平合作精神.
教学重点
教学难点
理解按一定比例来分配一个数量的意义,根据题中所给的比,掌握各部分量占总数量的几分之几,能熟练地求出各部分量.
理解并掌握按比分配应用题的数量关系.
年级班男生人数与女生人数的比是4 ∶5.
提示:可以把男生人数看作( ? ?)份,女生人数有( ? ? )份. 全班共有( ? ? )份.
男生人数是女生人数的( ? ? ),
女生人数是男生人数的( ? ? ?),
男生人数是全班总人数的( ? ? ),
女生人数是全班总人数的( ? ? ).
4
5
9
爸爸发送了一个100元的微信红包,小明抢到60元妈妈抢到40元。
小明抢到的金额与妈妈抢到的金额的比是( ? ? ? ? )。?
两个人互相说一说这个比的意义。?
3 : 2
按比分配
例2 这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液.
问题: (1)什么是稀释液?什么是浓缩液?
(2)浓度是1:2的稀释液怎么配制呢?
例2
问题: (1) 500 mL是谁的体积?
(2) 1:4表示什么?
(3)要解决的问题是什么?
例2
问题: (1)你能读懂线段图所表示的意思吗?
(2)你能试着独立解决吗?
例2
方法1:
① 总份数:4+1=5
② 每份是:4÷1=5(mL)
③ 浓缩液有:100×1=100(mL)
④ 水有:100×4=400(mL)
问题: (3)你知道两种解法中每一步求的是什么吗?
(4)两种解法有什么联系和区别?
方法2:
① 总份数:4+1=5
例2
方法1:
① 总份数:4+1=5
② 每份是:4÷1=5(mL)
③ 浓缩液有:100×1=100(mL)
④ 水有:100×4=400(mL)
方法2:
① 总份数:4+1=5
问题:如何检验解答是否正确呢?
(1)浓缩液+水=500 mL ? ?(2)浓缩液︰水=1:4
在日常生活和工农业生产中,常常需要把一个数量按照一定的比来进行分配,这种分配方法通常叫做按比分配.
“按比分配”解决问题
特点:
已知两个数(三个数)的和与这两个数(三个数)的比.
求这两个数(三个数)各是多少?
按比分配解决问题一般步骤(份数法)
分什么,有多少?
总数量
怎样分?
( )︰( )或( )︰( )︰( )
求平均分的总份数(前项+后项)
求每份是多少?(总数量÷总份数)
再求出每部分是多少?
按比分配解决问题一般步骤:(分数乘法)
分什么,有多少?
总数量
怎样分?
( )︰( )或( )︰( )︰( )
求平均分的总份数(前项+后项)
求每部分占总数量的几分之几是多少?
用分数乘法求出每部分是多少
转化成
1.某妇产医院上月新生儿303名,男女婴儿人数之比是51:50.
上月新生男、女婴儿各有多少人?
303÷(51+50)=3(人)?
3×51=153(人)?
3×50=150(人)?
答:上月新生男婴儿153人,女婴儿150人.
2.
200÷(1+9)=20(mL)
20×1=20(mL)
20×9=180(mL)
答:需要蜂蜜20mL,水180mL.
3.
一共有多少名游客?多少名救生员?
7+1=8
答:一共有49名游客,7名救生员.
4. 学校把栽70棵树的任务按照六年级三个班的人数分配给各班,一班有46人,二班有44人,三班有50人. 三个班各应栽多少棵数?
答:一班应栽23棵树,二班应栽22棵树, 三班应栽25棵树.
5. 比和除法、分数有什么关系?比的基本性质是什么?请化简下列各比.
24:36
2:3
0.75:1
3:4
5:6
答:比的前项相当于除法中的被除数,分数中的分子;比的后项相当于除法中的除数,分数中的分母;比号相当于除法中的除号,分数中的分数线;比值相当于除法中的商,分数的分值;不同的是:比是指两个量之间的关系;除法是一种运算;分数是一个数。比的基本性质:比的前项和后项同时乘或除以(0除外)相同的数,比值不变,这叫做比的基本性质.
6. 填空.
4
50
0.8
1.25
4
5
9
4
(3)20kg:0.2t的比值是( ? ? ).
7.
三种蔬菜的面积分别是多少平方米?
800-320=480(m?)
答:西红柿的面积是320m?、黄瓜的面积是320m?、茄子的面积是160m?.
8. 请你根据下面的信息,寻找合适的量,写出这些量之间的比.
参考答案?
我和爸爸的年龄比是6:19;?
爸爸和妈妈一年的工资的比是3:2.
9. 某仓库里储存了150t大米、60t面粉和15t杂粮,求这个仓库里储存的大米、面粉和杂粮的比. 并把它化成最简单的整数比.
大米:面粉:杂粮=150t:60t:15t
=150:60:15
=10:4:1
答:这个仓库里储存的大米、面粉和杂粮的比是150:60:15,化成最简整数比是10:4:1.
10. 搅拌混凝土需要水泥、沙子和石子共20t. 三种原料分别需要多少吨?
2+3+5=10
答:需要水泥4t,沙子6t,石子10t.
11. 用120cm的铁丝做成一个长方体的框架. 长、宽、高的比是3:2:1. 这个长方体的长、宽、高分别是多少?
120÷4=30(cm)
3+2+1=6
答:这个长方体的长是15cm,宽是10cm,高是5cm.
1.长方形的周长是10厘米,长与宽的比是4:1,这个长方形的宽是____厘米,长是____厘米.
10÷2×(4+1)=1(厘米),所以这个长方形的宽是1×1=1(厘米),长是1×4=4(厘米).
提高练习
2.做一个长方体的木箱,它的所有棱长之和为112分米,它的长、宽、高之比为6∶5∶3,这个木箱的体积是____立方分米.
112÷4=28(分米),28÷(6+5+3)=2(分米),则长方体的长为2×6=12(分米),宽为2×5=10(分米),高为2×3=6(分米),所以这个木箱的体积是12×10×6=720(立方分米).
提高练习
3.被减数、减数与差的和是80,减数和差的比是3∶5,差是____.
80÷(3+5+8)=5,所以差是5×5=25.
提高练习
1.养殖场里兔子的只数在180~200之间,白兔和黑兔的只数比是9:7,养殖场里白兔比黑兔多____只.
180÷(9+7)=11.25,则兔子的总只数16×12=192(只),所以养殖场里白兔比黑兔多192÷(9+7)×(9-7)=24(只).
拓展练习
2.A、B两种商品的价格比是7:3.如果它们的价格分别上涨70元,那么它们现在的价格比是7:4,A种商品原来的价格是____元.
拓展练习
3.甲、乙两包糖的重量比为4:1.从甲包取出130克放入乙包后,甲、乙两包糖的重量比为7:5.原来甲包有____克糖.
拓展练习
艺术中的黄金比
雕塑高2.04米,从肚脐到脚底高1.26米.
1.26︰2.04≈0.618
爱与美之神“维纳斯”,表现出最美的人.
a
b
断臂女神维纳斯
项目
女神维纳斯
艺术中的黄金比
著名画家达?芬奇的蒙娜丽莎构图就完美的体现了黄金比在油画艺术上的应用. 通过上面三幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都体现了黄金比,使得这幅油画看起来是那么的和谐完美.?
“检阅”西方的一一幅优美油画,它的画杠结构比例也正是0.618的比值.
艺术中的黄金比
音乐中的黄金比
音乐家发现,二胡演奏中,“千金”分弦的比符合0.618∶1时,奏出来的音调最和谐、最悦耳.
肖邦的《降D大调夜曲》全曲不计前奏共76小节,理论计算黄金分割点应在46小节,而再现部恰恰位于46小节,是全曲力度最强的高潮所在,真是巧夺天工!
