六年级上册数学课件-比的意义与基本性质 人教版(63张ppt)
文档属性
| 名称 | 六年级上册数学课件-比的意义与基本性质 人教版(63张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 20:17:48 | ||
图片预览









文档简介
比的意义
比的基本性质
例1
化简比
教学目标
经历从具体情境中抽象出比的过程,理解比的意义。
理解比的基本性质,掌握化简比的方法。
体会比的思想在生活中的广泛应用,感受数学与生活的联系,激发学生学习数学的热情。
教学重点
教学难点
理解比的意义,掌握化简比的方法。
理解比的意义。
?
?
?
?2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空。在太空中执行此次任务的航天员杨利伟在飞船里向人们展示了联合国旗和中华人民共和国国旗。
问题:(1)这两面旗子的长和宽各是多少?
(2)怎样用算式表示它们长和宽之间的倍数关系?
(3)长和宽的比怎样表示?宽和长的比呢?
(4)这两个比一样吗?都是长与宽进行比较,有什么不同?
15
cm
15
cm
10
cm
?
?
?
“神舟”五号进入运行轨道后,在距地350
km
的高空作圆周运动,平均90
分钟绕地球一周,大约
运行42252
km。
问题:
(1)怎样用算式表示飞船进入轨道后平均每分钟飞行多少千米?
(2)
42252÷90求出的是什么?
(3)“神舟”五号的飞行路程和时间可以写成比的形式吗?
(4)“神舟”五号的飞行路程和时间的比怎样表示?
15:10
10:15
42252:90
问题:
(1)以上各组比有什么相同点与不同点?
(2)什么是比?
小结比的意义:两个数的比表示两个数相除。
你画过或者动手做过国旗吗?
是不是随便剪个长方形,画上5个五角星就是一个规范的国旗呢?
这四幅图让它们做国旗的底板,你们觉得它们合适吗?为什么?
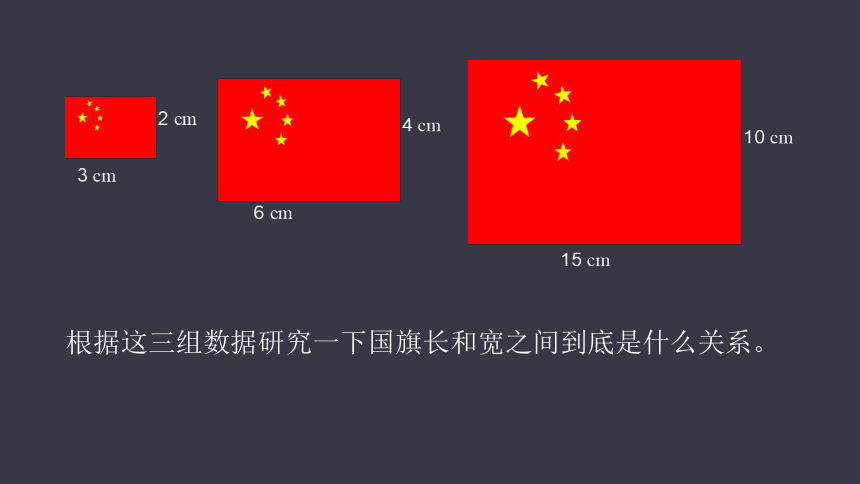
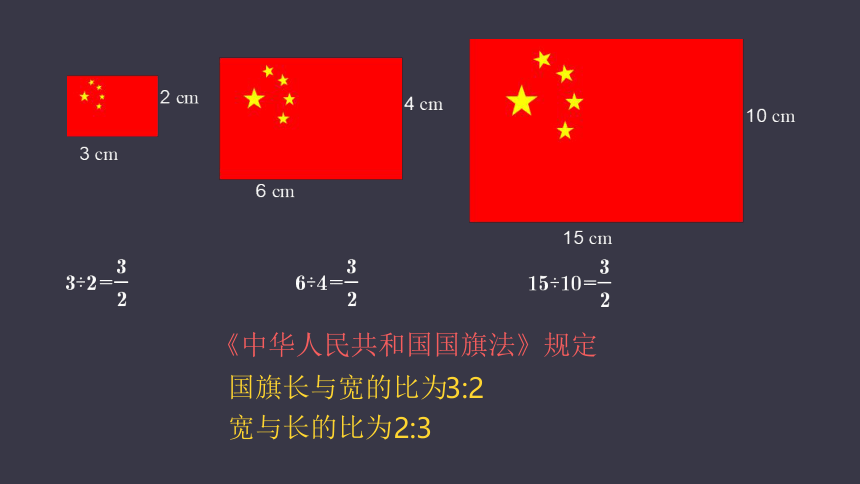
根据这三组数据研究一下国旗长和宽之间到底是什么关系。
《中华人民共和国国旗法》规定
国旗长与宽的比为
宽与长的比为
3:2
2:3
A
B
C
D
E
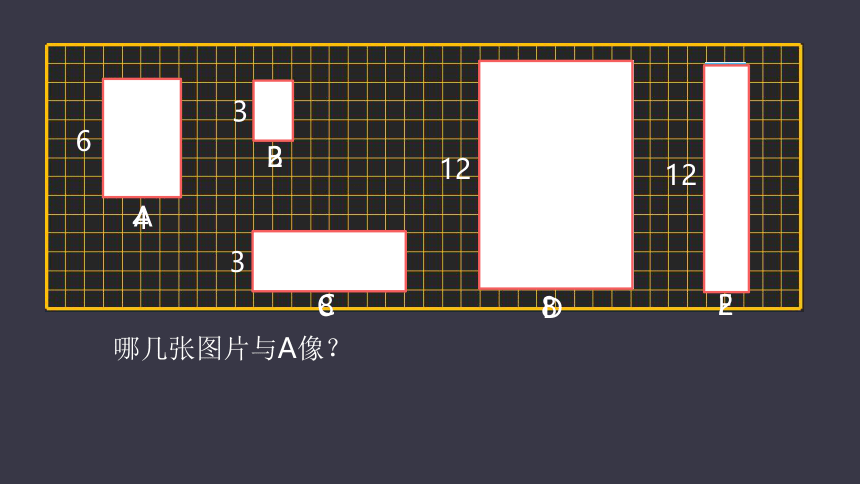
哪几张图片与A像?
6
4
3
2
8
12
2
12
3
8
两个数相除,又叫作这两个数的比。
6÷4
写作
6∶4
读作
6比4
比号
你能联系实际说说生活中有哪些比吗?
6∶4=6÷4=?
?
=1.5
.
.
.
生活中的脚印
脚长×6.876≈身高
问:你能根据这张脚印照片推断此人的身高吗?
案例中的脚印
问:你能根据这张脚印照片推断此人的身高吗?
依赖数据
关注关系
比?
比的认识
认识理解“比”
我是把10毫升蜂蜜加到90毫升水中的。
1份
蜂蜜
9份
水
蜂蜜的量和水的比是1:9
水的量和蜂蜜的比是9:1
蜂蜜和蜂蜜水的比是1:10
水的量和蜂蜜水的比是9:10
1毫升——160毫升
认识理解“比”
问:我们可以知道哪些信息?你是怎么理解这些比的?
1杯——160杯
1份——160份
2——?
认识理解“比”
4∶3
16∶9
问:你是怎么理解4∶3和16∶9的?
认识理解“比”
2杯香蕉原汁加3杯牛奶可以做成好喝的奶昔。
居里夫人提炼1克镭用了8吨沥青。
?
?
?
?在两个数的比中,“:”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
比的各部分名称
3
:
2
=
3
÷
2
=
前
项
比
号
后
项
比
值
比的后项可以是0吗?你的依据是什么?
比的价值
体会多个数量的连比。
?
?
?
?黑火药为中国古代四大发明之一。黑火药是由硝酸钾、硫磺和炭等组成的混合火药。10世纪中国《武经总要》所载三者配比为50︰25︰6.25(其他18.75)。
问:你是怎样理解这个比的?
用分数或除法容易表示它们之间的关系吗?
比的价值
一张照片引发的思考
?
?
?
?1964年《中国画报》封面刊出了一张照片。大庆油田的“铁人”王进喜头戴大狗皮帽,身穿厚棉袄,顶着鹅毛大雪,握着钻机手柄眺望远方,在他身后散布着星星点点的高大井架。
比的价值
日本有关部门
?
?
?
?通过照片中的扶手栏杆与反应塔的相对比例推断,该反应塔的直径大约为5米。
?
?
?
?根据反应塔的直径,推断出大庆炼油厂的年加工原油能力为100万吨。
?
?
?
?而据报道,当年大庆“已有820口油井出油”,年产原油360万吨,估计到1971年可增加到1200万吨。
比的价值
日本决策机构推断:
我国正需要日产一万吨的炼油设备。
?
?
?
?果不其然,没过多久,中国石油工业部就开始在全世界范围内购买,而日本的炼油设备以其有现货,价格低符合中国的实际生产能力而倍受欢迎,一举中标。(参王培智主编,《软科学知识词典》,中国展望出版社,1988)
比、除法、分数之间的联系
除法
比
分数
联?
?
?
?
系
前倾
后倾
比值
被除数
分子
除数
分母
商
分数值
不能为0
足球比赛中的比分3:0是数学中的比吗?
做一做
?
?
?
?小敏和小亮在文具店买同样的练习本。小敏买了6
本,共花了1.8
元。小亮买了8
本,共花了2.4
元。小敏和小亮的练习本数之比是(?
?
?):(?
?
?),比值是(?
?
?);花的钱数之比是(?
?
?
):(?
?
?
),比值是(?
?
?)。
3:(?
?
?)=24?
?
?
?
?
?
(?
?
?):
8=0.5
6
8
1.8
2.4
4
做一做
你还记得商不变的规律和分数的基本性质吗?
被除数和除数同时乘或除以相同的数(0除外),商的大小不变。
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
比的基本性质
小明、小强、小丽都喜欢玩折纸。有一天,他们三人在争论谁折纸鹤最快。
小明说:“我折的纸鹤数与时间(分)的比是6:8。”
小强说:“我折的纸鹤数与时间(分)的比是3:4。”
小丽说:“我折的纸鹤数与时间(分)的比是12:16。”
问题:小明、小强和小丽谁折得最快?
小明:6:8=6÷8=?
?
=
小强:3:4=3÷4=
小丽:12:16=12÷16=?
?
?=?
?
?
??
问题:(1)通过比较的过程你有什么发现?
(2)这三个比中有什么规律?
比的基本性质
比中有什么样的规律?请你借助学过的知识独立进行研究。
6÷8=(6×2)÷(8×2)=12÷16
6:8
=(6×2):(8×2)
=12:16
6:8
=(6÷2):(8÷2)
=3:4
6÷8=(6÷2)÷(8÷2)=3÷4
问题:你这样做的依据是什么?还可以借助哪些知识进行研究?
小结:比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
比的基本性质
?
?
?
?如
3:4
这样的前项和后项都是整数,而且又互质,这样的比就叫最简单整数比。
根据比的基本性质,可以把比化成最简单的整数比。
比的基本性质
记忆宝库
你还记得除法中有什么性质?分数中又有什么性质吗?
商不变的性质
2÷3=(2×2)÷(3×2)=4÷6
在除法里,被除数和除数同时乘以(或除以)
一个相同的数(0除外),商不变。
分数的基本性质
分数的分子和分母同时乘以(或除以)一个
相同的数(0除外),分数的大小不变。
比的基本性质
6︰8
=
6÷8
=?
?
?=?
?
?
??
6÷8=(6×2)÷(8×2)=12÷16
利用比和除法的关系来研究比中的规律。
6︰8
=(6×2)︰(8×2)=12︰16
6÷8=(6÷2)÷(8÷2)=
3÷4
6︰8
=(6÷2)︰(8÷2)=
3︰4
比的基本性质
4︰5
=
16︰20
=
40︰50
(4×4):(5×4)
(4×10):(5×10)
比的基本性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
比的基本性质
利用商不变性质,我们可以进行除法的简算。
根据分数的基本性质,我们可以把分数化成最简分数。
应用比的基本性质,我们可以把比化成最简单的整数比。
4︰6
=
2︰3?
前项、后项同时除以2
前、后项必须是整数,而且互质.
2
3
比的基本性质
例1
?
?
?
?(1)
“神舟”五号搭载了两面联合国旗,一面长15
cm,宽10
cm,另一面长180
cm,宽120
cm。这两面联合国旗的长和宽的最简单的整数比分别是多少?
例1
?
?
?
?(1)
“神舟”五号搭载了两面联合国旗,一面长15
cm,宽10
cm,另一面长180
cm,宽120
cm。这两面联合国旗的长和宽的最简单的整数比分别是多少?
15︰10
=
(15÷5)
︰(10÷5)
=3︰2
同时除以15和10的最大公约数
180︰120
=
(180÷60)
︰(120÷60)
=3︰2
同时除以180和120的最大公约数
例1
(2)把下面各比化成最简单的整数比。
0.75︰2
同时乘6和9的最小公倍数
=
0.75︰2
=
(0.75×100)︰(2×100)
=75︰200
=3︰400
=3︰8
不管哪种方法,最后的结果应该是一个最简的整数比,而不是一个数。
100
100
例1做一做
把下面各比化成最简单的整数比。
32:16
48:40
0.15:0.3
=(32÷16):
(16÷16)=2:1
=(48÷8):
(40÷8)=6:5
=(0.15×100):(0.3×100)=15︰30=1:2
=(?
?
?
×6):(?
?
?
×6)=5︰1
=(?
?
?
×24):(?
?
?
×24)=14︰9
=(0.125×1000):(?
?
?
×1000)=125︰625=1︰5
你知道吗?
?
?
?
?你听说过“黄金比”吗?
?
?
?
?把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为0.618:1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
a:b≈0.618:1
上图中的五角星内还有其他线段长度符合黄金比吗?
请你自己收集一下有关黄金比的信息与同学交流。
练习
(1)航海模型小组男女生人数的比是(?
?
?)
:(?
?
?),比值是(?
?
)。
(2)航空模型小组男女生人数的比是(?
?
?)
:(?
?
?),比值是(?
?
)。女生人数与小组总人数的比是(?
?):(?
?),比值是(?
?
)。
(3)汽车模型小组做的模型总数与人数的比是(?
?):(?
?),比值是(?
?
)。
7
4
5
8
5
13
3
2
练习
下面哪面红旗长与宽的比是3:2?
答:第②面红旗长与宽的比是3:2。
练习
求下面各比的比值。
5:9
0.6:0.1
练习
把下列各比化成后项是100的比。
(1)学校种植树苗,成活的棵树与种植总棵树的比是49:50。
(2)要配制一种药水,药剂的质量与药水总质量的比是0.12:1。
(3)某企业去年实际产值与计划产值的比是275万:250万。
49:50=98:100
0.12:1=12:100
275万:250万=275:250=(275÷2.5):(250÷2.5)=110:100
练习
不同蔬菜中钙和磷含量的比是不同的。
上面哪种蔬菜的钙、磷含量比较高?哪种最低?
芹菜:7:5=1.4
菠菜:2:1=2
茄子:23:20=1.15
1.15<1.4<2
答:菠菜的钙、磷含量比最高,茄子的钙、磷含量最低。
练习
小亮的说法对吗?正确的比应该是多少?你会化简吗?
我和表妹身高的比是155:1。
答:小亮的说法不对。
155cm:1m=155cm:100cm=31:20
练习
甲数和乙数的比是2:3,乙数和丙数的比是4:5。甲数和丙数的比是多少?
甲数:乙数=2:3=8:12
乙数:丙数=4:5=12:15
甲数:丙数=8:15
答:甲数和丙数的比是8:15。
练习
有一个两位数,十位上的数和个位上的数的比是2:3。十位上的数加上2,就和个位上的数相等。这个两位数是多少?
2÷(3-2)=2
2×2=4
2×3=6
4×10+6=46
答:这个两位数是46。
练习
答:如图,大、小长方形的面积比是6:4=3:2。
6:4=3:2
提高练习
把1克盐放入10克水中,盐和盐水的质量比是1:____.
两个正方形的边长比是1:2,这两个正方形面积比是____:____.
11
1
4
数a与数b的比是5:7,数b就比数a多百分之几?
提高练习
(7-5)÷5=40%
答:数b就比数a多40%。
提高练习
甲、乙、丙三名同学都向灾区同学捐了款.甲所捐的钱数与乙的比是3:2,乙所捐的钱数与丙的比是4:5,那么甲所捐的钱数与丙的比是____:____.
甲:乙=3:2=6:4,丙:乙=5:4,所以甲:丙=6:5,也就是甲所捐的钱数与丙的比是6:5.
拓展练行四边形ABCD被分成甲、乙、丙三个三角形,若BE=28,EC=16,那么甲、乙、丙的面积比是____:____:____.
由于三个三角形等高,所以甲、乙、丙的面积比是
28:(28+16):16=28:44:16=7:11:4.
拓展练习
减数相当于差的?
?
?,差与被减数的最简整数比是____:____.
根据题意,设减数是4份,差是9份,那被减数就是4+9=13份,所以差与被减数的最简整数比是9:13.
拓展练习
甲乙两圆相交,相交重合部分为阴影部分,非重合部分为空白部分?
?
.甲圆中空白部分的面积是甲圆的?
?
?,乙圆中空白部分的面积是乙圆的,甲圆与乙圆面积的比是____:____.
根据题意,得阴影部分面积占甲圆的1-?
?
=?
?
?,则S甲=3S阴,同理,可得阴影部分面积占乙圆的1-?
?
=?
?
,则S乙=?
?S阴,所以甲圆与乙圆的面积之比为3:?
?=9:7.
黄金比
埃及金字塔
巴黎圣母院
维纳斯
蒙娜丽莎
北京紫禁城
黄金比
a
b
著名的巴黎圣母院
建筑中的黄金比
≈0.673
项目
巴黎圣母院
黄金比
?
?
?
?实际中,它正面宽度和高度的比例是5∶8,它的每一扇窗户长宽比例也是如此,很接近0.618这个比值,因此它更显得庄严和谐,辉煌壮丽。
黄金比
巴台农神庙
a
b
≈0.673
项目
巴黎圣母院
黄金比
巴台农神庙
43︰69.5≈0.618
43米
69.5米
黄金比
115.2︰186.4≈0.618
顶点到底边中点的距离=186.4米
中心到底边的距离=115.2米
比的基本性质
例1
化简比
教学目标
经历从具体情境中抽象出比的过程,理解比的意义。
理解比的基本性质,掌握化简比的方法。
体会比的思想在生活中的广泛应用,感受数学与生活的联系,激发学生学习数学的热情。
教学重点
教学难点
理解比的意义,掌握化简比的方法。
理解比的意义。
?
?
?
?2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空。在太空中执行此次任务的航天员杨利伟在飞船里向人们展示了联合国旗和中华人民共和国国旗。
问题:(1)这两面旗子的长和宽各是多少?
(2)怎样用算式表示它们长和宽之间的倍数关系?
(3)长和宽的比怎样表示?宽和长的比呢?
(4)这两个比一样吗?都是长与宽进行比较,有什么不同?
15
cm
15
cm
10
cm
?
?
?
“神舟”五号进入运行轨道后,在距地350
km
的高空作圆周运动,平均90
分钟绕地球一周,大约
运行42252
km。
问题:
(1)怎样用算式表示飞船进入轨道后平均每分钟飞行多少千米?
(2)
42252÷90求出的是什么?
(3)“神舟”五号的飞行路程和时间可以写成比的形式吗?
(4)“神舟”五号的飞行路程和时间的比怎样表示?
15:10
10:15
42252:90
问题:
(1)以上各组比有什么相同点与不同点?
(2)什么是比?
小结比的意义:两个数的比表示两个数相除。
你画过或者动手做过国旗吗?
是不是随便剪个长方形,画上5个五角星就是一个规范的国旗呢?
这四幅图让它们做国旗的底板,你们觉得它们合适吗?为什么?
根据这三组数据研究一下国旗长和宽之间到底是什么关系。
《中华人民共和国国旗法》规定
国旗长与宽的比为
宽与长的比为
3:2
2:3
A
B
C
D
E
哪几张图片与A像?
6
4
3
2
8
12
2
12
3
8
两个数相除,又叫作这两个数的比。
6÷4
写作
6∶4
读作
6比4
比号
你能联系实际说说生活中有哪些比吗?
6∶4=6÷4=?
?
=1.5
.
.
.
生活中的脚印
脚长×6.876≈身高
问:你能根据这张脚印照片推断此人的身高吗?
案例中的脚印
问:你能根据这张脚印照片推断此人的身高吗?
依赖数据
关注关系
比?
比的认识
认识理解“比”
我是把10毫升蜂蜜加到90毫升水中的。
1份
蜂蜜
9份
水
蜂蜜的量和水的比是1:9
水的量和蜂蜜的比是9:1
蜂蜜和蜂蜜水的比是1:10
水的量和蜂蜜水的比是9:10
1毫升——160毫升
认识理解“比”
问:我们可以知道哪些信息?你是怎么理解这些比的?
1杯——160杯
1份——160份
2——?
认识理解“比”
4∶3
16∶9
问:你是怎么理解4∶3和16∶9的?
认识理解“比”
2杯香蕉原汁加3杯牛奶可以做成好喝的奶昔。
居里夫人提炼1克镭用了8吨沥青。
?
?
?
?在两个数的比中,“:”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
比的各部分名称
3
:
2
=
3
÷
2
=
前
项
比
号
后
项
比
值
比的后项可以是0吗?你的依据是什么?
比的价值
体会多个数量的连比。
?
?
?
?黑火药为中国古代四大发明之一。黑火药是由硝酸钾、硫磺和炭等组成的混合火药。10世纪中国《武经总要》所载三者配比为50︰25︰6.25(其他18.75)。
问:你是怎样理解这个比的?
用分数或除法容易表示它们之间的关系吗?
比的价值
一张照片引发的思考
?
?
?
?1964年《中国画报》封面刊出了一张照片。大庆油田的“铁人”王进喜头戴大狗皮帽,身穿厚棉袄,顶着鹅毛大雪,握着钻机手柄眺望远方,在他身后散布着星星点点的高大井架。
比的价值
日本有关部门
?
?
?
?通过照片中的扶手栏杆与反应塔的相对比例推断,该反应塔的直径大约为5米。
?
?
?
?根据反应塔的直径,推断出大庆炼油厂的年加工原油能力为100万吨。
?
?
?
?而据报道,当年大庆“已有820口油井出油”,年产原油360万吨,估计到1971年可增加到1200万吨。
比的价值
日本决策机构推断:
我国正需要日产一万吨的炼油设备。
?
?
?
?果不其然,没过多久,中国石油工业部就开始在全世界范围内购买,而日本的炼油设备以其有现货,价格低符合中国的实际生产能力而倍受欢迎,一举中标。(参王培智主编,《软科学知识词典》,中国展望出版社,1988)
比、除法、分数之间的联系
除法
比
分数
联?
?
?
?
系
前倾
后倾
比值
被除数
分子
除数
分母
商
分数值
不能为0
足球比赛中的比分3:0是数学中的比吗?
做一做
?
?
?
?小敏和小亮在文具店买同样的练习本。小敏买了6
本,共花了1.8
元。小亮买了8
本,共花了2.4
元。小敏和小亮的练习本数之比是(?
?
?):(?
?
?),比值是(?
?
?);花的钱数之比是(?
?
?
):(?
?
?
),比值是(?
?
?)。
3:(?
?
?)=24?
?
?
?
?
?
(?
?
?):
8=0.5
6
8
1.8
2.4
4
做一做
你还记得商不变的规律和分数的基本性质吗?
被除数和除数同时乘或除以相同的数(0除外),商的大小不变。
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
比的基本性质
小明、小强、小丽都喜欢玩折纸。有一天,他们三人在争论谁折纸鹤最快。
小明说:“我折的纸鹤数与时间(分)的比是6:8。”
小强说:“我折的纸鹤数与时间(分)的比是3:4。”
小丽说:“我折的纸鹤数与时间(分)的比是12:16。”
问题:小明、小强和小丽谁折得最快?
小明:6:8=6÷8=?
?
=
小强:3:4=3÷4=
小丽:12:16=12÷16=?
?
?=?
?
?
??
问题:(1)通过比较的过程你有什么发现?
(2)这三个比中有什么规律?
比的基本性质
比中有什么样的规律?请你借助学过的知识独立进行研究。
6÷8=(6×2)÷(8×2)=12÷16
6:8
=(6×2):(8×2)
=12:16
6:8
=(6÷2):(8÷2)
=3:4
6÷8=(6÷2)÷(8÷2)=3÷4
问题:你这样做的依据是什么?还可以借助哪些知识进行研究?
小结:比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
比的基本性质
?
?
?
?如
3:4
这样的前项和后项都是整数,而且又互质,这样的比就叫最简单整数比。
根据比的基本性质,可以把比化成最简单的整数比。
比的基本性质
记忆宝库
你还记得除法中有什么性质?分数中又有什么性质吗?
商不变的性质
2÷3=(2×2)÷(3×2)=4÷6
在除法里,被除数和除数同时乘以(或除以)
一个相同的数(0除外),商不变。
分数的基本性质
分数的分子和分母同时乘以(或除以)一个
相同的数(0除外),分数的大小不变。
比的基本性质
6︰8
=
6÷8
=?
?
?=?
?
?
??
6÷8=(6×2)÷(8×2)=12÷16
利用比和除法的关系来研究比中的规律。
6︰8
=(6×2)︰(8×2)=12︰16
6÷8=(6÷2)÷(8÷2)=
3÷4
6︰8
=(6÷2)︰(8÷2)=
3︰4
比的基本性质
4︰5
=
16︰20
=
40︰50
(4×4):(5×4)
(4×10):(5×10)
比的基本性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
比的基本性质
利用商不变性质,我们可以进行除法的简算。
根据分数的基本性质,我们可以把分数化成最简分数。
应用比的基本性质,我们可以把比化成最简单的整数比。
4︰6
=
2︰3?
前项、后项同时除以2
前、后项必须是整数,而且互质.
2
3
比的基本性质
例1
?
?
?
?(1)
“神舟”五号搭载了两面联合国旗,一面长15
cm,宽10
cm,另一面长180
cm,宽120
cm。这两面联合国旗的长和宽的最简单的整数比分别是多少?
例1
?
?
?
?(1)
“神舟”五号搭载了两面联合国旗,一面长15
cm,宽10
cm,另一面长180
cm,宽120
cm。这两面联合国旗的长和宽的最简单的整数比分别是多少?
15︰10
=
(15÷5)
︰(10÷5)
=3︰2
同时除以15和10的最大公约数
180︰120
=
(180÷60)
︰(120÷60)
=3︰2
同时除以180和120的最大公约数
例1
(2)把下面各比化成最简单的整数比。
0.75︰2
同时乘6和9的最小公倍数
=
0.75︰2
=
(0.75×100)︰(2×100)
=75︰200
=3︰400
=3︰8
不管哪种方法,最后的结果应该是一个最简的整数比,而不是一个数。
100
100
例1做一做
把下面各比化成最简单的整数比。
32:16
48:40
0.15:0.3
=(32÷16):
(16÷16)=2:1
=(48÷8):
(40÷8)=6:5
=(0.15×100):(0.3×100)=15︰30=1:2
=(?
?
?
×6):(?
?
?
×6)=5︰1
=(?
?
?
×24):(?
?
?
×24)=14︰9
=(0.125×1000):(?
?
?
×1000)=125︰625=1︰5
你知道吗?
?
?
?
?你听说过“黄金比”吗?
?
?
?
?把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为0.618:1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
a:b≈0.618:1
上图中的五角星内还有其他线段长度符合黄金比吗?
请你自己收集一下有关黄金比的信息与同学交流。
练习
(1)航海模型小组男女生人数的比是(?
?
?)
:(?
?
?),比值是(?
?
)。
(2)航空模型小组男女生人数的比是(?
?
?)
:(?
?
?),比值是(?
?
)。女生人数与小组总人数的比是(?
?):(?
?),比值是(?
?
)。
(3)汽车模型小组做的模型总数与人数的比是(?
?):(?
?),比值是(?
?
)。
7
4
5
8
5
13
3
2
练习
下面哪面红旗长与宽的比是3:2?
答:第②面红旗长与宽的比是3:2。
练习
求下面各比的比值。
5:9
0.6:0.1
练习
把下列各比化成后项是100的比。
(1)学校种植树苗,成活的棵树与种植总棵树的比是49:50。
(2)要配制一种药水,药剂的质量与药水总质量的比是0.12:1。
(3)某企业去年实际产值与计划产值的比是275万:250万。
49:50=98:100
0.12:1=12:100
275万:250万=275:250=(275÷2.5):(250÷2.5)=110:100
练习
不同蔬菜中钙和磷含量的比是不同的。
上面哪种蔬菜的钙、磷含量比较高?哪种最低?
芹菜:7:5=1.4
菠菜:2:1=2
茄子:23:20=1.15
1.15<1.4<2
答:菠菜的钙、磷含量比最高,茄子的钙、磷含量最低。
练习
小亮的说法对吗?正确的比应该是多少?你会化简吗?
我和表妹身高的比是155:1。
答:小亮的说法不对。
155cm:1m=155cm:100cm=31:20
练习
甲数和乙数的比是2:3,乙数和丙数的比是4:5。甲数和丙数的比是多少?
甲数:乙数=2:3=8:12
乙数:丙数=4:5=12:15
甲数:丙数=8:15
答:甲数和丙数的比是8:15。
练习
有一个两位数,十位上的数和个位上的数的比是2:3。十位上的数加上2,就和个位上的数相等。这个两位数是多少?
2÷(3-2)=2
2×2=4
2×3=6
4×10+6=46
答:这个两位数是46。
练习
答:如图,大、小长方形的面积比是6:4=3:2。
6:4=3:2
提高练习
把1克盐放入10克水中,盐和盐水的质量比是1:____.
两个正方形的边长比是1:2,这两个正方形面积比是____:____.
11
1
4
数a与数b的比是5:7,数b就比数a多百分之几?
提高练习
(7-5)÷5=40%
答:数b就比数a多40%。
提高练习
甲、乙、丙三名同学都向灾区同学捐了款.甲所捐的钱数与乙的比是3:2,乙所捐的钱数与丙的比是4:5,那么甲所捐的钱数与丙的比是____:____.
甲:乙=3:2=6:4,丙:乙=5:4,所以甲:丙=6:5,也就是甲所捐的钱数与丙的比是6:5.
拓展练行四边形ABCD被分成甲、乙、丙三个三角形,若BE=28,EC=16,那么甲、乙、丙的面积比是____:____:____.
由于三个三角形等高,所以甲、乙、丙的面积比是
28:(28+16):16=28:44:16=7:11:4.
拓展练习
减数相当于差的?
?
?,差与被减数的最简整数比是____:____.
根据题意,设减数是4份,差是9份,那被减数就是4+9=13份,所以差与被减数的最简整数比是9:13.
拓展练习
甲乙两圆相交,相交重合部分为阴影部分,非重合部分为空白部分?
?
.甲圆中空白部分的面积是甲圆的?
?
?,乙圆中空白部分的面积是乙圆的,甲圆与乙圆面积的比是____:____.
根据题意,得阴影部分面积占甲圆的1-?
?
=?
?
?,则S甲=3S阴,同理,可得阴影部分面积占乙圆的1-?
?
=?
?
,则S乙=?
?S阴,所以甲圆与乙圆的面积之比为3:?
?=9:7.
黄金比
埃及金字塔
巴黎圣母院
维纳斯
蒙娜丽莎
北京紫禁城
黄金比
a
b
著名的巴黎圣母院
建筑中的黄金比
≈0.673
项目
巴黎圣母院
黄金比
?
?
?
?实际中,它正面宽度和高度的比例是5∶8,它的每一扇窗户长宽比例也是如此,很接近0.618这个比值,因此它更显得庄严和谐,辉煌壮丽。
黄金比
巴台农神庙
a
b
≈0.673
项目
巴黎圣母院
黄金比
巴台农神庙
43︰69.5≈0.618
43米
69.5米
黄金比
115.2︰186.4≈0.618
顶点到底边中点的距离=186.4米
中心到底边的距离=115.2米
