五年级上册数学课件- 解方程(2)人教版( 49张PPT)
文档属性
| 名称 | 五年级上册数学课件- 解方程(2)人教版( 49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 21:22:34 | ||
图片预览









文档简介
解方程例4、例5
教学目标
经历解方程的过程,理解方程的解和解方程的意义。
能运用等式的性质解方程会正确解形如ax±b=c,a(x+b)=c的方程。
能运用所学知识解决简单的实际问题,感受数学与现实生活的密切联系。
解方程。
复习解方程
3.5x=10.5
解:3.5x÷3.5=10.5÷3.5
x=3
43-x=24
解:43-x+x=24+x
43=24+x
24+x=43
24+x-24=43-24
x=19
问题:你解方程的依据是什么?需要注意什么?
教学重点
理解在解方程过程中,把一个式子看作一个整体。
教学难点
理解解方程的方法。
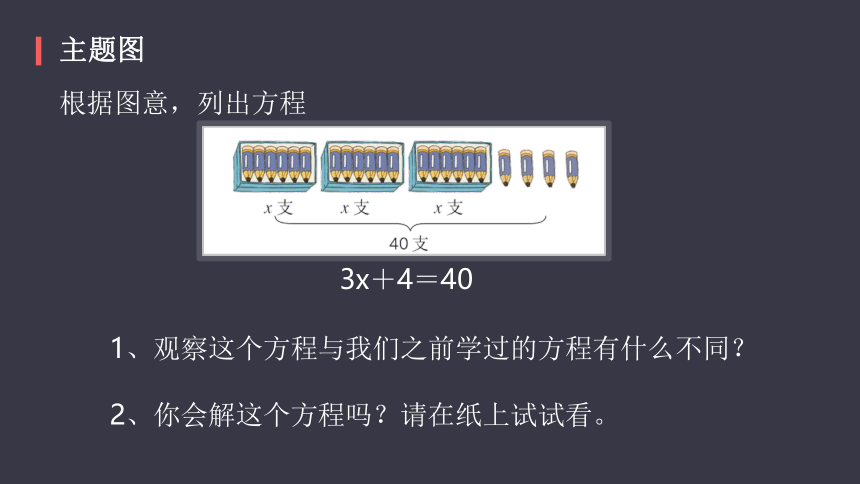
主题图
根据图意,列出方程
3x+4=40
1、观察这个方程与我们之前学过的方程有什么不同?
2、你会解这个方程吗?请在纸上试试看。
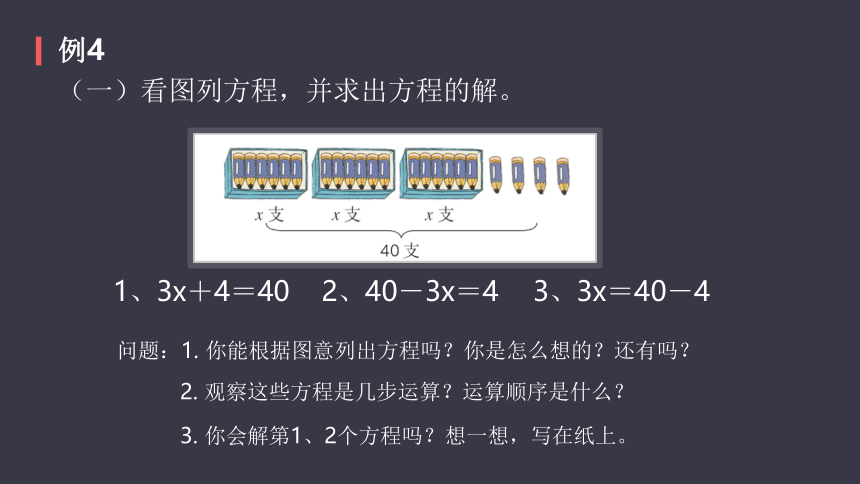
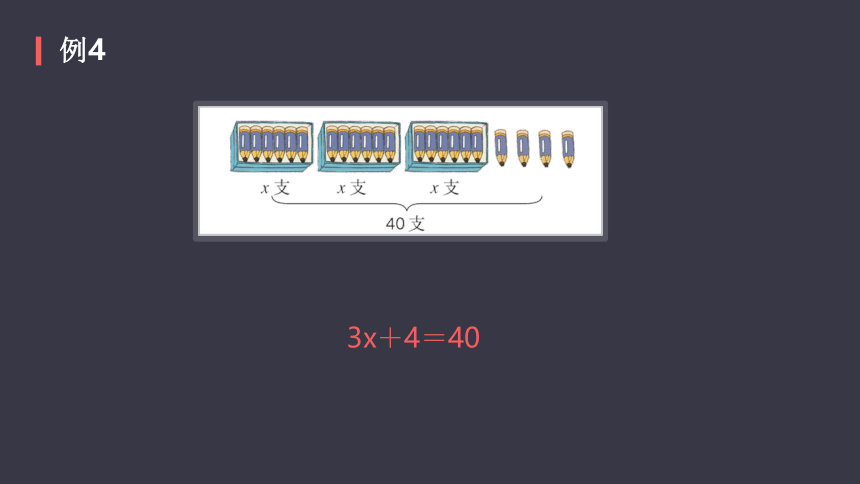
例4
1、3x+4=40
2、40-3x=4
3、3x=40-4
问题:1. 你能根据图意列出方程吗?你是怎么想的?还有吗?
2. 观察这些方程是几步运算?运算顺序是什么?
3. 你会解第1、2个方程吗?想一想,写在纸上。
(一)看图列方程,并求出方程的解。
(二)解决问题,分享方法
例4
3x+4=40
解:3x+4-4=40-4
3x=36
3x÷3=36÷3
x=12
问题:1. 观察这个方程,可以先把什么看成一个整体?
2. 说说你在解方程时分为几大步?依据什么?要达到什么目的?
例4
(二)解决问题,分享方法
40-3x=4
解:40-3x+3x=4+3x
40=4+3x
4+3x=40
4+3x-4=40-4
3x=36
3x÷3=36÷3
x=12
问题:1. 观察这个方程,可以先把什么看成一个整体?
2. 说说你在解方程时分为几大步?依据什么?要达到什么目的?
例4
(三)反思检验
3x+4=40
方程左边=3x+4
=3×12+4
=36+4
=40
=方程右边
所以,x =12是方程的解。
问题: x=12是不是方程的解?请你检验一下。
例4
3x+4=40
例4
3x+4=40
解:3x=40-4
3x=36
x=36÷3
x=12
第一步 加数=和-另一个加数
第二步 算出3x的积
第三步 因数=积÷另一个因数
第四步 得出x的解
1、观察这个方程的解题过程,在解方程时我们可以先把什么看成一个整体?
2、为什么?
因为方程左边的3x+4是个乘加综合算式,运算顺序是先算乘3x ,最后算加,所以等是最后的和,所以先把3x看作一个整体.也就是先把3x看作一个加数.号右边的40?
先把3x看作一个整体.也就是先把3x看作一个加数.
加数=和-另一个加数,就可以算出3x 的积。
例4
3x+4=40
解:3x=40-4
3x=36
x=36÷3
x=12
第一步 加数=和-另一个加数
第二步 算出3x的积
第三步 因数=积÷另一个因数
第四步 得出x的解
1、第一步中为什么方程右边-4?这是根据什么来做的?
2、第三步中为什么方程右边÷3?这又是根据什么来做的?
先把3x看作一个整体.也就是先把3x看作一个加数.
再用“加数=和-另一个加数” 算出3x的积。
因数=积÷另一个因数
例4
(三)反思检验
x=12是不是方程的解?请你检验一下。
3x+4=40
方程左边=3x+4
=3×12+4
=36+4
=40
= 方程右边
所以,x =12是方程的解。
检验:
最后总结由你完成:
例4
之前学的都是一步就能解决的方程题,今天学习的是解两步、三步,甚至更多步的方程时,你有什么感悟?和大家分享一下。
①方程左边是乘加或乘减算式,先把乘法ax看做整体,先得出这个整体ax是多少,再求出x的值。
例4
方程变形,你还会吗?请你尝试,并能说说你是如何做的?
因为方程左边的40-3x是个乘减综合算式,运算顺序是先算乘3x ,最后算减,所以等号右边的4是最后的差,所以先把3x看作一个整体.也就是先把3x看作一个减数.
40-3x=4
解:3x=40-4
3x =36
x=36÷3
x=12
第一步 减数=被减数-差
第二步算出3x的积
第三步因数=积÷另一个因数
第四步 得出x的解
5x+1.5=7.5??
做一做
x=1.2
例5
解方程 2(x-16)=8
预设1:
预设2:
解:2(x-16)÷2=8÷2
x-16=4
x-16+16=4+16
x=20
解:2 x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
解方程 2(x-16)=8
例5
1. 观察这个方程有几步运算?可以把什么看做一个整体?你还能想到什么?
2. 你能运用等式的性质解方程吗?请你写一写。
问题:
请你自己把这个方程解完。
例5
解方程 2(x-16)=8
预设1:
预设2:
解:2(x-16)÷2=8÷2
x-16=4
x-16+16=4+16
x=20
解:2 x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
问题:
你能说说他们的想法吗?他们分别把什么看做一个整体?分几大步解决?运用了什么运算定律?
例5
(三)反思检验
2(x-16)=8
方程左边=2(x-16)?
=2×4
=方程右边
所以,x=20是方程的解。
=2×(20-16)
=8
别忘了检验!
问题: x=20是不是方程的解?请你检验一下。
做一做
2. 解方程。
6x-35=13
解: 6x-35+35=13+35
6x=48
6x÷6=48÷6
x=8
3x-42×6=6
解:3x-252=6
3x-252+252=6+252
3x=258
3x÷3=258÷3
x=86
1. 你能说说他们的想法吗?分别把什么看做一个整体?分几大步解决?依据是什么??
2. 请你检验一下。
小结:在解两步、三步方程时,你有什么感悟?和大家分享一下。
问题:
(5x-12)×8=24
做一做
解:(5x-12)×8÷8=24÷8
5x-12=3
5x-12+12=3+12
5x=15
5x÷5=15÷5
x=3
(100-3x)÷2=8
解:(100-3x)÷2×2=8×2
100-3x+3x=16+3x
100=16+3x
16+3x=100
16+3x-16=100-16
3x=84
x=28
1. 你能说说他们的想法吗?分几大步解决?分别把什么看做一个整体?依据是什么?
2. 请你检验一下。
小结:在解两步、三步方程时,你有什么感悟?和大家分享一下。
问题:
做一做
方程左边=(5x-12)×8
=(5×3-12)×8
=3×8
=24
=方程右边
所以,x=3是方程的解。
方程左边=(100-3x)÷2
=(100-3×28)÷2
=16÷2
=8
=方程右边
所以,x=28是方程的解。
检验:
检验:
练习十五
8. 看图列方程,并求出方程的解。
x+50=200
x=200-50
x=150
60+2x=158
2x=158-60
x=98÷2
x=49
解:
解:
(1)
(2)
9. 解下列方程。
练习十五
6x+3=9
4x-2=10
5x-39=56
18+5x=21
8x-4×14=0
7x÷3=8.19
6x=9-3
x=6÷6
x=1
4x=10+2
x=12÷4
x=3
5x=56+39
x=95÷5
x=19
5x=21-18
x=3÷5
x=0.6
8x=56
x=56÷8
x=7
7x=8.19×3
x=24.57÷7
x=3.51
解:
解:
解:
解:
解:
解:
练习十五
x+13=33
7(x-20)=140
1.8x=54
6.7x-60.3=6.7
9x+x=0
x=0
x=10
x=20
x=30
x=40
10. 把下面每个方程和它的解连起来。
练习十五
周长36m
xm
5m
共80人
成人:
儿童:
x
x
x
x
(x+5)×2=36
x+5=36÷2
x=13
3x+x=80
4x=80
x=20
解
解
11. 看图列方程并求解。
练习十五
12. 解下列方程。
4(6x+3)=60
2x+23×4=134
(3x-4)×5=4
2x+1.5x=17.5
8x-3x=105
3x+x+6=26
6x+3=60÷4
x=2
6x=15-3
2x+92=134
2x=134-92
x=21
3x-4=4÷5
x=1.6
3x=0.8+4
3.5x=17.5
x=17.5÷3.5
x=5
5x=105
x=105÷5
x=21
4x+6=26
4x=26-6
x=5
解
解
解
解
解
解
练习十五
13. 在○里填上“>”“<”或“=”。
(1)当x=50时,2x-16?
(2)当x=5时,4x+3x
(3)当x=2.5时,7x-3x
(4)当x=15时,(5x-12)÷3?
(5x+12)÷3
>
<
=
>
>
=
<
>
68,2x+16
68。
35,4+3x
35。
10,7x+3x
10。
25,
25。
练习十五
14. 在□里填上适当的数,使每个方程的解都是x=5。
+x=13
=2.3
x-
×x=7
=50
x÷
8
2.7
1.4
0.1
数学游戏
1、选择
提高练习
演出服原价x元,降价了19元,现价89元,求原价的正确方程是:( )
A x+19=89
B 89-19=x
C x-19=89
D 89-x=19
C
2. 已知算式:x-a=( ),求
提高练习
(1)当x=( )时,算式的结果是0。
(2)当x=( )时,算式的结果是a。
可以怎样想?
x-a=0,我可以求出方程的解。
预设1:x-a=0
x-a+a=0+a
x=a
我想到:相等的两个数相减等于0。
预设2:因为a-a=0
所以x=a
你能想到什么?
a
2a
提高练习
3、在○里填上合适的数,使x=5。
-x=2.88
÷x=3.1
7.88
15.5
拓展练习
1、填空。
问题:说说你是怎么想的?
已知
+
+
=16
+
=12
那么
=( )
=( )
4
8
拓展练习
不计算,下列方程中代表数值最大的字母是( ),
最小的字母是( )。
A ×20=160
B÷2=80
C+12=80
D-234=12
当X=6时,4(X+□)=80时,□表示( )
A 16
B 20
C 14
D
A
C
拓展练习
3. 猜数游戏:你会猜数吗?把你的想法表示出来。
你先想一个数,再乘以6,减去5.只要告诉我结果,我就能猜出你想的数
结果是139
24
方程史
方程的思想可追溯到伟大的数学家笛卡儿,他在《指导思维的法则》一书中提出了一种解决一切问题的“万能方法”,其模式是:
1.把任何种类的问题转化为数学问题;
2.把任何种类的数学问题转化为代数问题;
3.把任何种类的代数问题转化为方程(组)问题;然后讨论方程(组)的问题,得到解之后再对其进行
方程史
今有上禾三秉,中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾实一秉各几何?”依术文列出方程如下
方程史
方程史
方程史
《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
3x+2y=19
x+4y=23.
类似地,图2所示的算筹图我们可以表述为?
方程史
我国古代数学家刘微注释“方程”的含义时,曾解释“方”字与上述数字方阵有密切关系,而“程”字则 指列出含有未知数的等式。所以说汉语中“方程”一词最早来源于列一组含有未知数的等式解决实际问题的方法
方程史
刘徽从事数学研究时,中国创造的十进位记数法和计算工具“算筹”已经使用一千多年了。在世界各种各样的记数法中,十进位记数法是最先进、最方便的。中国古代数学知识的结晶“九章算术”也成书三百多年了。“九章算术”反映的是中国先民在生产劳动、丈量土地和测量容积等实践活动中所创造的数学知识,包括方田、粟米、哀分、少广、商功、均输、盈不足、方程、勾股九章,是中国古代算法的基础,它含有上百个计算公式和246个应用问题,有完整的分数四则运算法则,比例和比例分配算法,若干面积、体积公式,开平方、开立方程序,方程术--线性方程组解法,正负数加减法则,解勾股形公式和简单的测望问题算法。其中许多成就处于世界领先地位。公元元年前年,盛极一时的古希腊数学走向衰微,“九章算术”的出现,标志着世界数学研究中心从地中海沿岸转到了中国,开创了东方以应用数学为中心占据世界数学舞台主导地位千余年的局面。
方程史
1914年美国总统威尔逊提请国会将每年五月份的第二星期天定母亲节
2012年5曰13日是第98个母亲节小明班很多同学都给妈妈准备了鲜花和礼物,求一朵鲜花的价格要用一元一次方程解一束鲜花和两个礼盒55元,两束鲜花和三个礼盒90元,用一元一次方程解
方程史
方程是一种数学工具
可以通过列方程来求解“鸡兔同笼”问题,相比较小学学的凑数办法及奥数中的假设归一的办法,哪种方法更易理解授受.
方程史
小学学过奥数,奥数学的较好的学生中,会有一部分学生排斥列方程解题,甚至觉得奥数的方法才是最简洁的方法.对于初一所涉及到一些方程应用题来说,的确如此,但在初二的《勾股定理》、初三的《相似》这两章中,会涉及较多有关几何图形的计算问题(线段长度、角度),而利用方程则使解答过程清晰明了,直接式计算则难度极大.
利用等式性质解方程拓展(一)
利用等式性质解方程拓展(二)
教学目标
经历解方程的过程,理解方程的解和解方程的意义。
能运用等式的性质解方程会正确解形如ax±b=c,a(x+b)=c的方程。
能运用所学知识解决简单的实际问题,感受数学与现实生活的密切联系。
解方程。
复习解方程
3.5x=10.5
解:3.5x÷3.5=10.5÷3.5
x=3
43-x=24
解:43-x+x=24+x
43=24+x
24+x=43
24+x-24=43-24
x=19
问题:你解方程的依据是什么?需要注意什么?
教学重点
理解在解方程过程中,把一个式子看作一个整体。
教学难点
理解解方程的方法。
主题图
根据图意,列出方程
3x+4=40
1、观察这个方程与我们之前学过的方程有什么不同?
2、你会解这个方程吗?请在纸上试试看。
例4
1、3x+4=40
2、40-3x=4
3、3x=40-4
问题:1. 你能根据图意列出方程吗?你是怎么想的?还有吗?
2. 观察这些方程是几步运算?运算顺序是什么?
3. 你会解第1、2个方程吗?想一想,写在纸上。
(一)看图列方程,并求出方程的解。
(二)解决问题,分享方法
例4
3x+4=40
解:3x+4-4=40-4
3x=36
3x÷3=36÷3
x=12
问题:1. 观察这个方程,可以先把什么看成一个整体?
2. 说说你在解方程时分为几大步?依据什么?要达到什么目的?
例4
(二)解决问题,分享方法
40-3x=4
解:40-3x+3x=4+3x
40=4+3x
4+3x=40
4+3x-4=40-4
3x=36
3x÷3=36÷3
x=12
问题:1. 观察这个方程,可以先把什么看成一个整体?
2. 说说你在解方程时分为几大步?依据什么?要达到什么目的?
例4
(三)反思检验
3x+4=40
方程左边=3x+4
=3×12+4
=36+4
=40
=方程右边
所以,x =12是方程的解。
问题: x=12是不是方程的解?请你检验一下。
例4
3x+4=40
例4
3x+4=40
解:3x=40-4
3x=36
x=36÷3
x=12
第一步 加数=和-另一个加数
第二步 算出3x的积
第三步 因数=积÷另一个因数
第四步 得出x的解
1、观察这个方程的解题过程,在解方程时我们可以先把什么看成一个整体?
2、为什么?
因为方程左边的3x+4是个乘加综合算式,运算顺序是先算乘3x ,最后算加,所以等是最后的和,所以先把3x看作一个整体.也就是先把3x看作一个加数.号右边的40?
先把3x看作一个整体.也就是先把3x看作一个加数.
加数=和-另一个加数,就可以算出3x 的积。
例4
3x+4=40
解:3x=40-4
3x=36
x=36÷3
x=12
第一步 加数=和-另一个加数
第二步 算出3x的积
第三步 因数=积÷另一个因数
第四步 得出x的解
1、第一步中为什么方程右边-4?这是根据什么来做的?
2、第三步中为什么方程右边÷3?这又是根据什么来做的?
先把3x看作一个整体.也就是先把3x看作一个加数.
再用“加数=和-另一个加数” 算出3x的积。
因数=积÷另一个因数
例4
(三)反思检验
x=12是不是方程的解?请你检验一下。
3x+4=40
方程左边=3x+4
=3×12+4
=36+4
=40
= 方程右边
所以,x =12是方程的解。
检验:
最后总结由你完成:
例4
之前学的都是一步就能解决的方程题,今天学习的是解两步、三步,甚至更多步的方程时,你有什么感悟?和大家分享一下。
①方程左边是乘加或乘减算式,先把乘法ax看做整体,先得出这个整体ax是多少,再求出x的值。
例4
方程变形,你还会吗?请你尝试,并能说说你是如何做的?
因为方程左边的40-3x是个乘减综合算式,运算顺序是先算乘3x ,最后算减,所以等号右边的4是最后的差,所以先把3x看作一个整体.也就是先把3x看作一个减数.
40-3x=4
解:3x=40-4
3x =36
x=36÷3
x=12
第一步 减数=被减数-差
第二步算出3x的积
第三步因数=积÷另一个因数
第四步 得出x的解
5x+1.5=7.5??
做一做
x=1.2
例5
解方程 2(x-16)=8
预设1:
预设2:
解:2(x-16)÷2=8÷2
x-16=4
x-16+16=4+16
x=20
解:2 x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
解方程 2(x-16)=8
例5
1. 观察这个方程有几步运算?可以把什么看做一个整体?你还能想到什么?
2. 你能运用等式的性质解方程吗?请你写一写。
问题:
请你自己把这个方程解完。
例5
解方程 2(x-16)=8
预设1:
预设2:
解:2(x-16)÷2=8÷2
x-16=4
x-16+16=4+16
x=20
解:2 x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
问题:
你能说说他们的想法吗?他们分别把什么看做一个整体?分几大步解决?运用了什么运算定律?
例5
(三)反思检验
2(x-16)=8
方程左边=2(x-16)?
=2×4
=方程右边
所以,x=20是方程的解。
=2×(20-16)
=8
别忘了检验!
问题: x=20是不是方程的解?请你检验一下。
做一做
2. 解方程。
6x-35=13
解: 6x-35+35=13+35
6x=48
6x÷6=48÷6
x=8
3x-42×6=6
解:3x-252=6
3x-252+252=6+252
3x=258
3x÷3=258÷3
x=86
1. 你能说说他们的想法吗?分别把什么看做一个整体?分几大步解决?依据是什么??
2. 请你检验一下。
小结:在解两步、三步方程时,你有什么感悟?和大家分享一下。
问题:
(5x-12)×8=24
做一做
解:(5x-12)×8÷8=24÷8
5x-12=3
5x-12+12=3+12
5x=15
5x÷5=15÷5
x=3
(100-3x)÷2=8
解:(100-3x)÷2×2=8×2
100-3x+3x=16+3x
100=16+3x
16+3x=100
16+3x-16=100-16
3x=84
x=28
1. 你能说说他们的想法吗?分几大步解决?分别把什么看做一个整体?依据是什么?
2. 请你检验一下。
小结:在解两步、三步方程时,你有什么感悟?和大家分享一下。
问题:
做一做
方程左边=(5x-12)×8
=(5×3-12)×8
=3×8
=24
=方程右边
所以,x=3是方程的解。
方程左边=(100-3x)÷2
=(100-3×28)÷2
=16÷2
=8
=方程右边
所以,x=28是方程的解。
检验:
检验:
练习十五
8. 看图列方程,并求出方程的解。
x+50=200
x=200-50
x=150
60+2x=158
2x=158-60
x=98÷2
x=49
解:
解:
(1)
(2)
9. 解下列方程。
练习十五
6x+3=9
4x-2=10
5x-39=56
18+5x=21
8x-4×14=0
7x÷3=8.19
6x=9-3
x=6÷6
x=1
4x=10+2
x=12÷4
x=3
5x=56+39
x=95÷5
x=19
5x=21-18
x=3÷5
x=0.6
8x=56
x=56÷8
x=7
7x=8.19×3
x=24.57÷7
x=3.51
解:
解:
解:
解:
解:
解:
练习十五
x+13=33
7(x-20)=140
1.8x=54
6.7x-60.3=6.7
9x+x=0
x=0
x=10
x=20
x=30
x=40
10. 把下面每个方程和它的解连起来。
练习十五
周长36m
xm
5m
共80人
成人:
儿童:
x
x
x
x
(x+5)×2=36
x+5=36÷2
x=13
3x+x=80
4x=80
x=20
解
解
11. 看图列方程并求解。
练习十五
12. 解下列方程。
4(6x+3)=60
2x+23×4=134
(3x-4)×5=4
2x+1.5x=17.5
8x-3x=105
3x+x+6=26
6x+3=60÷4
x=2
6x=15-3
2x+92=134
2x=134-92
x=21
3x-4=4÷5
x=1.6
3x=0.8+4
3.5x=17.5
x=17.5÷3.5
x=5
5x=105
x=105÷5
x=21
4x+6=26
4x=26-6
x=5
解
解
解
解
解
解
练习十五
13. 在○里填上“>”“<”或“=”。
(1)当x=50时,2x-16?
(2)当x=5时,4x+3x
(3)当x=2.5时,7x-3x
(4)当x=15时,(5x-12)÷3?
(5x+12)÷3
>
<
=
>
>
=
<
>
68,2x+16
68。
35,4+3x
35。
10,7x+3x
10。
25,
25。
练习十五
14. 在□里填上适当的数,使每个方程的解都是x=5。
+x=13
=2.3
x-
×x=7
=50
x÷
8
2.7
1.4
0.1
数学游戏
1、选择
提高练习
演出服原价x元,降价了19元,现价89元,求原价的正确方程是:( )
A x+19=89
B 89-19=x
C x-19=89
D 89-x=19
C
2. 已知算式:x-a=( ),求
提高练习
(1)当x=( )时,算式的结果是0。
(2)当x=( )时,算式的结果是a。
可以怎样想?
x-a=0,我可以求出方程的解。
预设1:x-a=0
x-a+a=0+a
x=a
我想到:相等的两个数相减等于0。
预设2:因为a-a=0
所以x=a
你能想到什么?
a
2a
提高练习
3、在○里填上合适的数,使x=5。
-x=2.88
÷x=3.1
7.88
15.5
拓展练习
1、填空。
问题:说说你是怎么想的?
已知
+
+
=16
+
=12
那么
=( )
=( )
4
8
拓展练习
不计算,下列方程中代表数值最大的字母是( ),
最小的字母是( )。
A ×20=160
B÷2=80
C+12=80
D-234=12
当X=6时,4(X+□)=80时,□表示( )
A 16
B 20
C 14
D
A
C
拓展练习
3. 猜数游戏:你会猜数吗?把你的想法表示出来。
你先想一个数,再乘以6,减去5.只要告诉我结果,我就能猜出你想的数
结果是139
24
方程史
方程的思想可追溯到伟大的数学家笛卡儿,他在《指导思维的法则》一书中提出了一种解决一切问题的“万能方法”,其模式是:
1.把任何种类的问题转化为数学问题;
2.把任何种类的数学问题转化为代数问题;
3.把任何种类的代数问题转化为方程(组)问题;然后讨论方程(组)的问题,得到解之后再对其进行
方程史
今有上禾三秉,中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾实一秉各几何?”依术文列出方程如下
方程史
方程史
方程史
《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
3x+2y=19
x+4y=23.
类似地,图2所示的算筹图我们可以表述为?
方程史
我国古代数学家刘微注释“方程”的含义时,曾解释“方”字与上述数字方阵有密切关系,而“程”字则 指列出含有未知数的等式。所以说汉语中“方程”一词最早来源于列一组含有未知数的等式解决实际问题的方法
方程史
刘徽从事数学研究时,中国创造的十进位记数法和计算工具“算筹”已经使用一千多年了。在世界各种各样的记数法中,十进位记数法是最先进、最方便的。中国古代数学知识的结晶“九章算术”也成书三百多年了。“九章算术”反映的是中国先民在生产劳动、丈量土地和测量容积等实践活动中所创造的数学知识,包括方田、粟米、哀分、少广、商功、均输、盈不足、方程、勾股九章,是中国古代算法的基础,它含有上百个计算公式和246个应用问题,有完整的分数四则运算法则,比例和比例分配算法,若干面积、体积公式,开平方、开立方程序,方程术--线性方程组解法,正负数加减法则,解勾股形公式和简单的测望问题算法。其中许多成就处于世界领先地位。公元元年前年,盛极一时的古希腊数学走向衰微,“九章算术”的出现,标志着世界数学研究中心从地中海沿岸转到了中国,开创了东方以应用数学为中心占据世界数学舞台主导地位千余年的局面。
方程史
1914年美国总统威尔逊提请国会将每年五月份的第二星期天定母亲节
2012年5曰13日是第98个母亲节小明班很多同学都给妈妈准备了鲜花和礼物,求一朵鲜花的价格要用一元一次方程解一束鲜花和两个礼盒55元,两束鲜花和三个礼盒90元,用一元一次方程解
方程史
方程是一种数学工具
可以通过列方程来求解“鸡兔同笼”问题,相比较小学学的凑数办法及奥数中的假设归一的办法,哪种方法更易理解授受.
方程史
小学学过奥数,奥数学的较好的学生中,会有一部分学生排斥列方程解题,甚至觉得奥数的方法才是最简洁的方法.对于初一所涉及到一些方程应用题来说,的确如此,但在初二的《勾股定理》、初三的《相似》这两章中,会涉及较多有关几何图形的计算问题(线段长度、角度),而利用方程则使解答过程清晰明了,直接式计算则难度极大.
利用等式性质解方程拓展(一)
利用等式性质解方程拓展(二)
