1.2 图形的全等 课件(共29张PPT)
文档属性
| 名称 | 1.2 图形的全等 课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-27 00:00:00 | ||
图片预览






文档简介
第一章 三角形
2 图形的全等
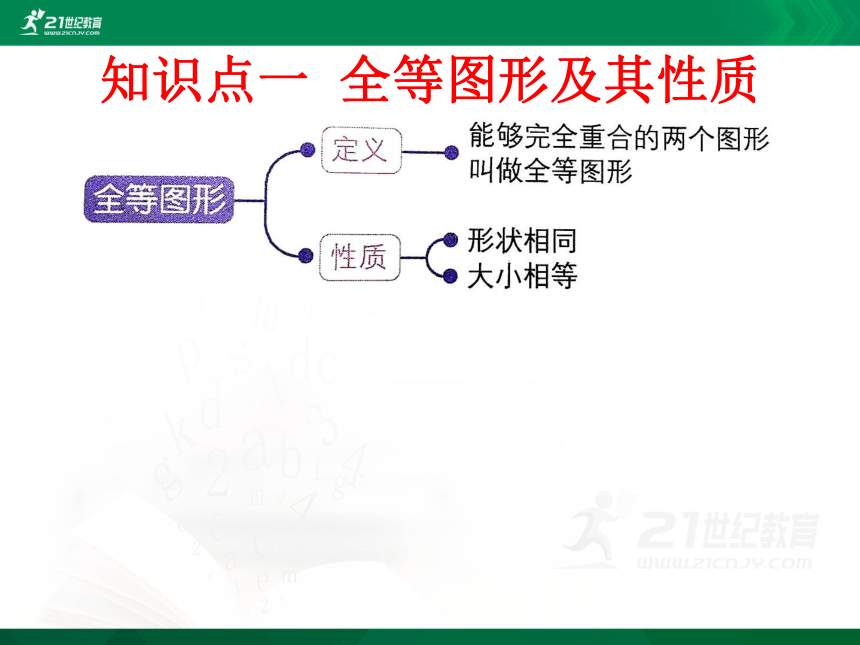
知识点一 全等图形及其性质
知识点一 全等图形及其性质
知识详解
(1)全等图形关注的是两个图形的形状和大小,而不是图形所在的位置,即把两个图形叠合在一起,看是否能够完全重合,能够完全重合则为全等图形.
(2)一个图形经过平移、旋转、翻折后,位置发生了变化,但形状和大小没有发生变化,因此平移、旋转、翻折前后的两个图形是全等图形.
(3)全等图形的面积、周长均相等,但面积或周长相等的两个图形不一定是全等图形.
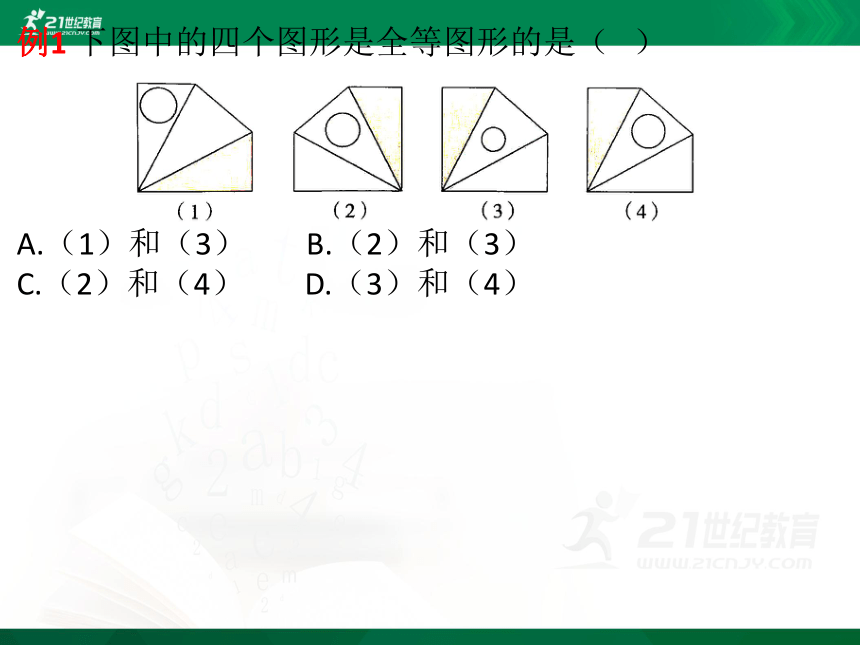
例1 下图中的四个图形是全等图形的是( )
A.(1)和(3) B.(2)和(3)
C.(2)和(4) D.(3)和(4)
例1 下图中的四个图形是全等图形的是( )
A.(1)和(3) B.(2)和(3)
C.(2)和(4) D.(3)和(4)
解析 能够完全重合的两个图形叫做全等图形.由图可得,(2)、(3)、(4)中的圆形在中间的三角形上,(1)中的圆形在一边,所以排除(1);观察(2)、(3)、(4)中的圆,很明显(3)中的圆小于(2)、(4)中的圆,所以排除(3);所以能够完全重合的两个图形是(2)和(4).故选C.
例1 下图中的四个图形是全等图形的是( C )
A.(1)和(3) B.(2)和(3)
C.(2)和(4) D.(3)和(4)
解析 能够完全重合的两个图形叫做全等图形.由图可得,(2)、(3)、(4)中的圆形在中间的三角形上,(1)中的圆形在一边,所以排除(1);观察(2)、(3)、(4)中的圆,很明显(3)中的圆小于(2)、(4)中的圆,所以排除(3);所以能够完全重合的两个图形是(2)和(4).故选C.
例1 下图中的四个图形是全等图形的是( C )
A.(1)和(3) B.(2)和(3)
C.(2)和(4) D.(3)和(4)
解析 能够完全重合的两个图形叫做全等图形.由图可得,(2)、(3)、(4)中的圆形在中间的三角形上,(1)中的圆形在一边,所以排除(1);观察(2)、(3)、(4)中的圆,很明显(3)中的圆小于(2)、(4)中的圆,所以排除(3);所以能够完全重合的两个图形是(2)和(4).故选C.
点拨 做题时要认真观察图形,若两个图形能完全重合,则它们是全等图形.
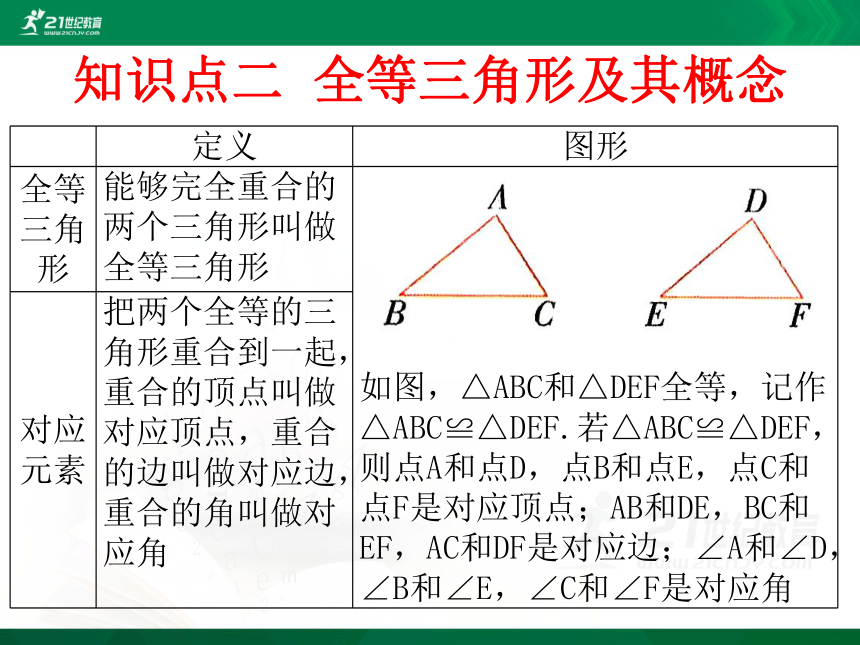
知识点二 全等三角形及其概念
定义
图形
全等
三角形
能够完全重合的两个三角形叫做全等三角形
如图,△ABC和△DEF全等,记作△ABC≌△DEF.若△ABC≌△DEF,则点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角
对应
元素
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角
技巧点拨
寻找全等三角形的对应元素的方法:一般地,在两个全等的三角形中,最大的角是对应角,最小的角是对应角;最长的边是对应边,最短的边是对应边;公共角、对顶角是对应角,公共边是对应边.
定义
图形
全等三角形的基本类型
平移型全等
对称型全等
旋转型全等
温馨提示
(1)全等三角形是全等图形中的一种.
(2)全等三角形用全等符号表示时,要把对应顶点的字母写在对应的位置上.
(3)对应边和对应角是相对于两个图形而言的,而对边和对角是指同一个三角形中的边角关系,对边指三角形中某个角(或顶点)所对的边,对角指三角形中某条边所对的角.
例2 如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他的对应边和对应角.
例2 如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他的对应边和对应角.
解析 ∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,∴其他的对应边有AN与AM,BN与CM,其他的对应角有∠BAN与∠CAM,∠ANB与∠AMC.
例2 如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他的对应边和对应角.
解析 ∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,∴其他的对应边有AN与AM,BN与CM,其他的对应角有∠BAN与∠CAM,∠ANB与∠AMC.
点拨 全等三角形中,对应边所对的角是对应角,对应角所对的边是对应边.
知识点三 全等三角形的性质
知识点三 全等三角形的性质
知识详解
(1)全等三角形的周长及面积相等;
(2)全等三角形对应的角平分线相等,对应边上的高相等,对应边上的中线相等.
例3 如图所示,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
例3 如图所示,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
解析(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,∴AB∥DE.
(2)∵△ABC≌△DEF,∴AB=DE=6,
∵OE=4,∴OD=DE-OE=6-4=2.
例3 如图所示,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
解析(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,∴AB∥DE.
(2)∵△ABC≌△DEF,∴AB=DE=6,
∵OE=4,∴OD=DE-OE=6-4=2.
点拨 在说明线段相等、角相等或求线段长、角的度数的这类问题时,常会用到全等三角形的性质.
经典例题
题型 运用全等三角形的性质求角度及线段长
例题 如图所示,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小;
(2)若AD=11cm,BC=5cm,求AB的长.
题型 运用全等三角形的性质求角度及线段长
例题 如图所示,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小;
(2)若AD=11cm,BC=5cm,求AB的长.
解析 (1)∵BE⊥AD,∴∠EBD=90°,
∵△ACF≌△DBE,∴∠FCA=∠EBD=90°,
∴∠A=90°-∠F=27°.
(2)∵△ACF≌△DBE,∴CA=BD,
∴ CA-CB=BD-BC,即AB=CD,
∵AD=11 cm, BC=5 cm,∴AB+CD=11-5=6cm,∴AB=3cm.
题型 运用全等三角形的性质求角度及线段长
例题 如图所示,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小;
(2)若AD=11cm,BC=5cm,求AB的长.
解析 (1)∵BE⊥AD,∴∠EBD=90°,
∵△ACF≌△DBE,∴∠FCA=∠EBD=90°,
∴∠A=90°-∠F=27°.
(2)∵△ACF≌△DBE,∴CA=BD,
∴ CA-CB=BD-BC,即AB=CD,
∵AD=11 cm, BC=5 cm,∴AB+CD=11-5=6cm,∴AB=3cm.
点拨 利用全等三角形的性质求线段长和角的度数,关键是找准对应边和对应角.
易错易混
易错点 在全等三角形中,找错对对应边
在确定全等三角形的对应边、对应角时,受思维定式的影响而找错对应边、对应角,导致出错.
例题 已知△ABC与△A’B’C’全等,其中∠A=60°,∠B’=40°,∠A’=80°,BC=3,则A’B’的值( )
A.为3 B.为4 C.为5 D.不确定
例题 已知△ABC与△A’B’C’全等,其中∠A=60°,∠B’=40°,∠A’=80°,BC=3,则A’B’的值( )
A.为3 B.为4 C.为5 D.不确定
解析 因为∠A’+∠B’+∠C’=180°,∠B’=40°,∠A’=80°,所以∠C’=180°-80°-40°=60°,所以∠C’=∠A,即∠C’与∠A是对应角,所以它们的对边A’B’与BC是对应边.因为BC=3,所以AB=3.
例题 已知△ABC与△A’B’C’全等,其中∠A=60°,∠B’=40°,∠A’=80°,BC=3,则A’B’的值( B )
A.为3 B.为4 C.为5 D.不确定
解析 因为∠A’+∠B’+∠C’=180°,∠B’=40°,∠A’=80°,所以∠C’=180°-80°-40°=60°,所以∠C’=∠A,即∠C’与∠A是对应角,所以它们的对边A’B’与BC是对应边.因为BC=3,所以AB=3.
例题 已知△ABC与△A’B’C’全等,其中∠A=60°,∠B’=40°,∠A’=80°,BC=3,则A’B’的值( B )
A.为3 B.为4 C.为5 D.不确定
解析 因为∠A’+∠B’+∠C’=180°,∠B’=40°,∠A’=80°,所以∠C’=180°-80°-40°=60°,所以∠C’=∠A,即∠C’与∠A是对应角,所以它们的对边A’B’与BC是对应边.因为BC=3,所以AB=3.
易错分析
全等三角形中,对应角的对边是对应边,本题易受思维定式的影响,误认为A’B’=AB.
2 图形的全等
知识点一 全等图形及其性质
知识点一 全等图形及其性质
知识详解
(1)全等图形关注的是两个图形的形状和大小,而不是图形所在的位置,即把两个图形叠合在一起,看是否能够完全重合,能够完全重合则为全等图形.
(2)一个图形经过平移、旋转、翻折后,位置发生了变化,但形状和大小没有发生变化,因此平移、旋转、翻折前后的两个图形是全等图形.
(3)全等图形的面积、周长均相等,但面积或周长相等的两个图形不一定是全等图形.
例1 下图中的四个图形是全等图形的是( )
A.(1)和(3) B.(2)和(3)
C.(2)和(4) D.(3)和(4)
例1 下图中的四个图形是全等图形的是( )
A.(1)和(3) B.(2)和(3)
C.(2)和(4) D.(3)和(4)
解析 能够完全重合的两个图形叫做全等图形.由图可得,(2)、(3)、(4)中的圆形在中间的三角形上,(1)中的圆形在一边,所以排除(1);观察(2)、(3)、(4)中的圆,很明显(3)中的圆小于(2)、(4)中的圆,所以排除(3);所以能够完全重合的两个图形是(2)和(4).故选C.
例1 下图中的四个图形是全等图形的是( C )
A.(1)和(3) B.(2)和(3)
C.(2)和(4) D.(3)和(4)
解析 能够完全重合的两个图形叫做全等图形.由图可得,(2)、(3)、(4)中的圆形在中间的三角形上,(1)中的圆形在一边,所以排除(1);观察(2)、(3)、(4)中的圆,很明显(3)中的圆小于(2)、(4)中的圆,所以排除(3);所以能够完全重合的两个图形是(2)和(4).故选C.
例1 下图中的四个图形是全等图形的是( C )
A.(1)和(3) B.(2)和(3)
C.(2)和(4) D.(3)和(4)
解析 能够完全重合的两个图形叫做全等图形.由图可得,(2)、(3)、(4)中的圆形在中间的三角形上,(1)中的圆形在一边,所以排除(1);观察(2)、(3)、(4)中的圆,很明显(3)中的圆小于(2)、(4)中的圆,所以排除(3);所以能够完全重合的两个图形是(2)和(4).故选C.
点拨 做题时要认真观察图形,若两个图形能完全重合,则它们是全等图形.
知识点二 全等三角形及其概念
定义
图形
全等
三角形
能够完全重合的两个三角形叫做全等三角形
如图,△ABC和△DEF全等,记作△ABC≌△DEF.若△ABC≌△DEF,则点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角
对应
元素
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角
技巧点拨
寻找全等三角形的对应元素的方法:一般地,在两个全等的三角形中,最大的角是对应角,最小的角是对应角;最长的边是对应边,最短的边是对应边;公共角、对顶角是对应角,公共边是对应边.
定义
图形
全等三角形的基本类型
平移型全等
对称型全等
旋转型全等
温馨提示
(1)全等三角形是全等图形中的一种.
(2)全等三角形用全等符号表示时,要把对应顶点的字母写在对应的位置上.
(3)对应边和对应角是相对于两个图形而言的,而对边和对角是指同一个三角形中的边角关系,对边指三角形中某个角(或顶点)所对的边,对角指三角形中某条边所对的角.
例2 如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他的对应边和对应角.
例2 如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他的对应边和对应角.
解析 ∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,∴其他的对应边有AN与AM,BN与CM,其他的对应角有∠BAN与∠CAM,∠ANB与∠AMC.
例2 如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他的对应边和对应角.
解析 ∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,∴其他的对应边有AN与AM,BN与CM,其他的对应角有∠BAN与∠CAM,∠ANB与∠AMC.
点拨 全等三角形中,对应边所对的角是对应角,对应角所对的边是对应边.
知识点三 全等三角形的性质
知识点三 全等三角形的性质
知识详解
(1)全等三角形的周长及面积相等;
(2)全等三角形对应的角平分线相等,对应边上的高相等,对应边上的中线相等.
例3 如图所示,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
例3 如图所示,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
解析(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,∴AB∥DE.
(2)∵△ABC≌△DEF,∴AB=DE=6,
∵OE=4,∴OD=DE-OE=6-4=2.
例3 如图所示,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
解析(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,∴AB∥DE.
(2)∵△ABC≌△DEF,∴AB=DE=6,
∵OE=4,∴OD=DE-OE=6-4=2.
点拨 在说明线段相等、角相等或求线段长、角的度数的这类问题时,常会用到全等三角形的性质.
经典例题
题型 运用全等三角形的性质求角度及线段长
例题 如图所示,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小;
(2)若AD=11cm,BC=5cm,求AB的长.
题型 运用全等三角形的性质求角度及线段长
例题 如图所示,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小;
(2)若AD=11cm,BC=5cm,求AB的长.
解析 (1)∵BE⊥AD,∴∠EBD=90°,
∵△ACF≌△DBE,∴∠FCA=∠EBD=90°,
∴∠A=90°-∠F=27°.
(2)∵△ACF≌△DBE,∴CA=BD,
∴ CA-CB=BD-BC,即AB=CD,
∵AD=11 cm, BC=5 cm,∴AB+CD=11-5=6cm,∴AB=3cm.
题型 运用全等三角形的性质求角度及线段长
例题 如图所示,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小;
(2)若AD=11cm,BC=5cm,求AB的长.
解析 (1)∵BE⊥AD,∴∠EBD=90°,
∵△ACF≌△DBE,∴∠FCA=∠EBD=90°,
∴∠A=90°-∠F=27°.
(2)∵△ACF≌△DBE,∴CA=BD,
∴ CA-CB=BD-BC,即AB=CD,
∵AD=11 cm, BC=5 cm,∴AB+CD=11-5=6cm,∴AB=3cm.
点拨 利用全等三角形的性质求线段长和角的度数,关键是找准对应边和对应角.
易错易混
易错点 在全等三角形中,找错对对应边
在确定全等三角形的对应边、对应角时,受思维定式的影响而找错对应边、对应角,导致出错.
例题 已知△ABC与△A’B’C’全等,其中∠A=60°,∠B’=40°,∠A’=80°,BC=3,则A’B’的值( )
A.为3 B.为4 C.为5 D.不确定
例题 已知△ABC与△A’B’C’全等,其中∠A=60°,∠B’=40°,∠A’=80°,BC=3,则A’B’的值( )
A.为3 B.为4 C.为5 D.不确定
解析 因为∠A’+∠B’+∠C’=180°,∠B’=40°,∠A’=80°,所以∠C’=180°-80°-40°=60°,所以∠C’=∠A,即∠C’与∠A是对应角,所以它们的对边A’B’与BC是对应边.因为BC=3,所以AB=3.
例题 已知△ABC与△A’B’C’全等,其中∠A=60°,∠B’=40°,∠A’=80°,BC=3,则A’B’的值( B )
A.为3 B.为4 C.为5 D.不确定
解析 因为∠A’+∠B’+∠C’=180°,∠B’=40°,∠A’=80°,所以∠C’=180°-80°-40°=60°,所以∠C’=∠A,即∠C’与∠A是对应角,所以它们的对边A’B’与BC是对应边.因为BC=3,所以AB=3.
例题 已知△ABC与△A’B’C’全等,其中∠A=60°,∠B’=40°,∠A’=80°,BC=3,则A’B’的值( B )
A.为3 B.为4 C.为5 D.不确定
解析 因为∠A’+∠B’+∠C’=180°,∠B’=40°,∠A’=80°,所以∠C’=180°-80°-40°=60°,所以∠C’=∠A,即∠C’与∠A是对应角,所以它们的对边A’B’与BC是对应边.因为BC=3,所以AB=3.
易错分析
全等三角形中,对应角的对边是对应边,本题易受思维定式的影响,误认为A’B’=AB.
