七年级数学多边形内角和
图片预览


文档简介
(共19张PPT)
多边形的内角和
多边形的内角和
凤凰中学:
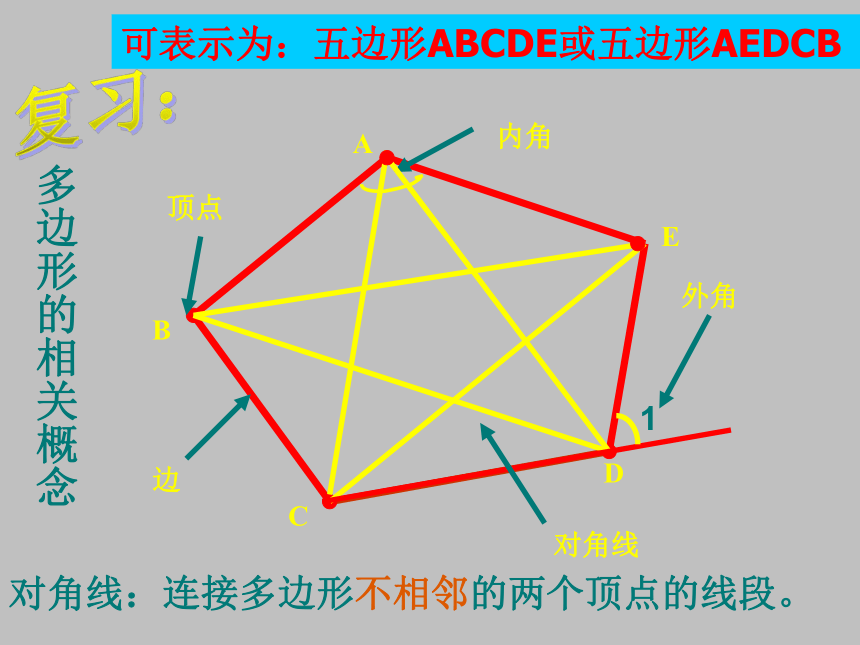
内角
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
多边形的相关概念
顶点
边
问题2:你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度?
(三角形内角和 180°)
(都是360°)
想一想
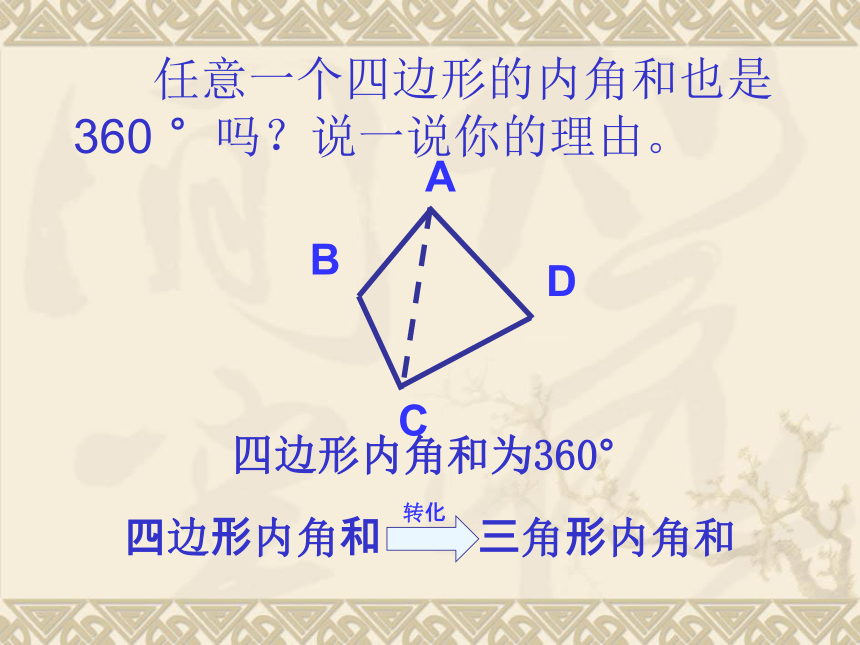
任意一个四边形的内角和也是360 °吗?说一说你的理由。
四边形内角和为360°
四边形内角和 三角形内角和
转化
A
B
C
D
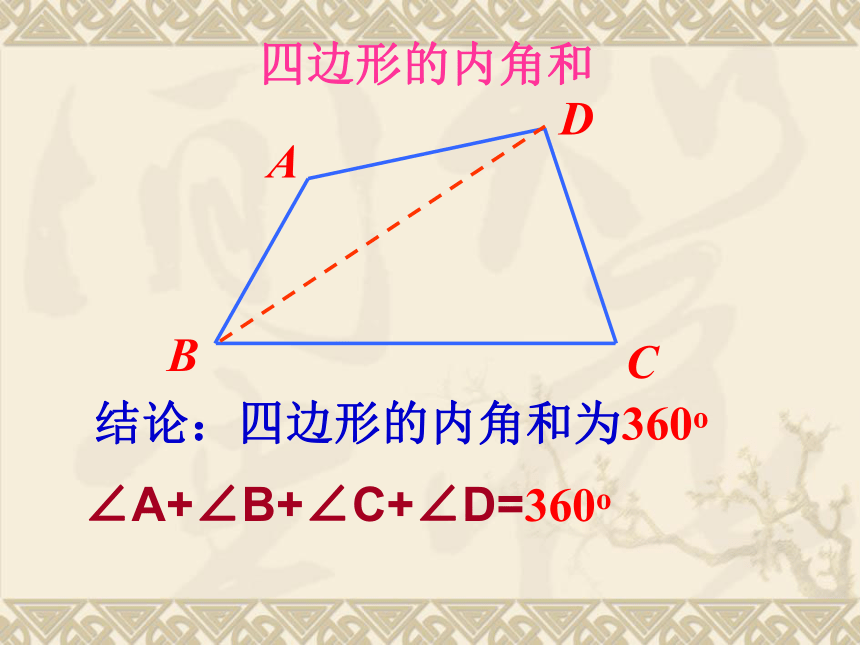
四边形的内角和
A
D
C
B
结论:四边形的内角和为360o
∠A+∠B+∠C+∠D=360o
B
A
C
D
E
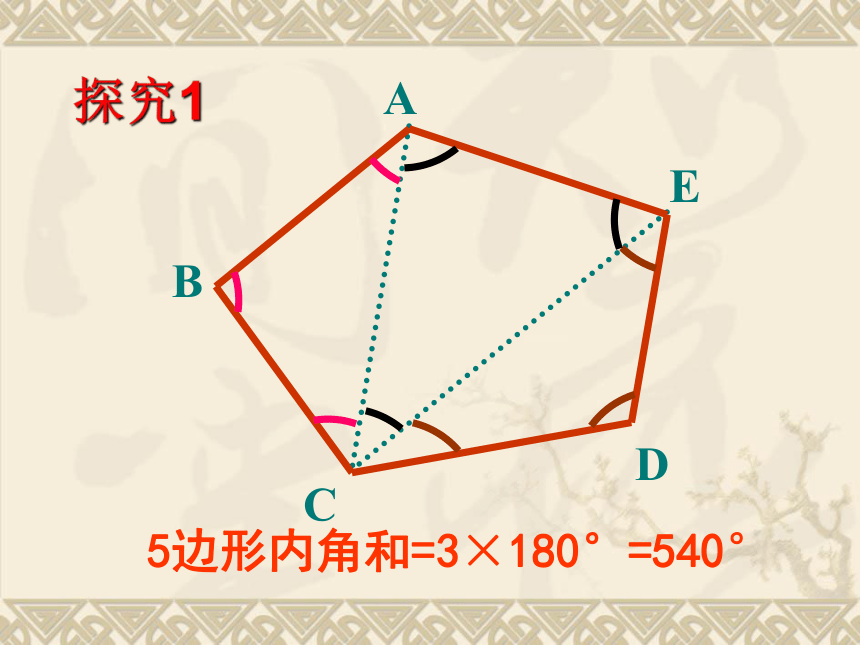
探究1
5边形内角和=3×180°=540°
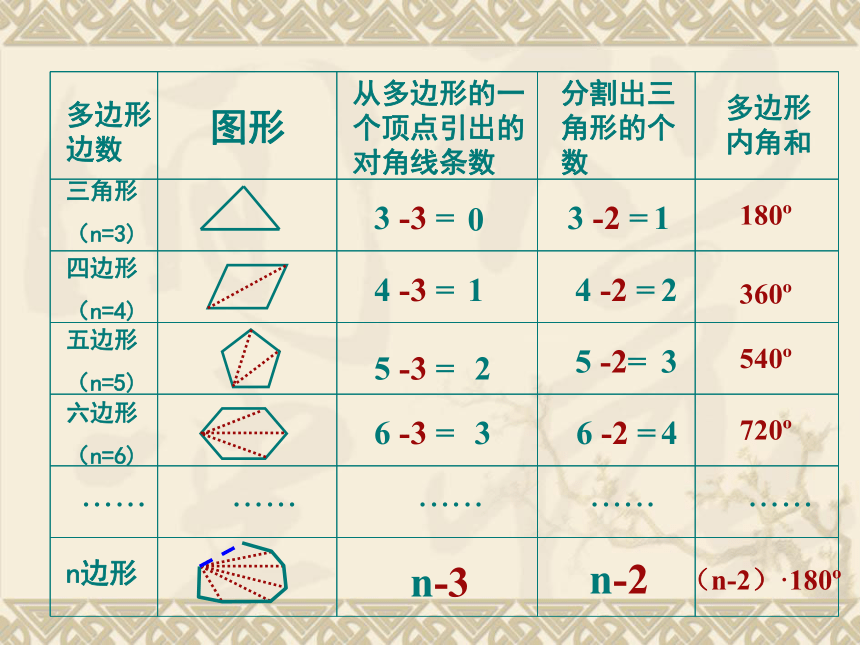
多边形边数
图形
从多边形的一个顶点引出的对角线条数
分割出三角形的个数
多边形内角和
三角形
(n=3)
四边形
(n=4)
五边形
(n=5)
六边形
(n=6)
n边形
······
······
······
······
······
0
3 -3 =
4 -3 =
5 -3 =
6 -3 =
n-3
1
2
3
3 -2 =
1
4 -2 =
2
5 -2=
3
6 -2 =
4
n-2
(n-2)·180
180
360
540
720
结论:n边形内角和公式为:_________。
B
A
C
D
G
F
E
(n-2)·180°
①n代表什么?
② n-2表示什么含义?
③为什么要乘以180°
应用新知
1、求八边形的内角和的度数。
解:八边形的内角和是
(n-2)×1800
= (8-2)×1800
= 10800
答:八边形的内角和的度数是1080o。
2、一个多边形内角和等于1260°,它是几边形?
解:设它是n边形,根据题意,得
(n-2)· 180= 1260
解得 n =9
所以它是九边形。
3.求下列图形中x的值:
∟
(1)
∟
(2)
(3)
C
A
B
D
E
(4)
AB∥CD
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?
D
A
B
C
解: 如右图,四边形ABCD中,
∠A+∠C=180°.
∵ ∠A+∠B+∠C+∠D
=(4-2) ×180°
=360 °
∴ ∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补.
布置作业:
习题7.3 5 、7 、 8
感悟与收获
这堂课你收获了什么?
把一个多边形分成几个三角形,还有其他分法吗?由新的分法能得出多边形内角和公式吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °= (n-2)×180 °
多边形的内角和
多边形的内角和
凤凰中学:
内角
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
多边形的相关概念
顶点
边
问题2:你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度?
(三角形内角和 180°)
(都是360°)
想一想
任意一个四边形的内角和也是360 °吗?说一说你的理由。
四边形内角和为360°
四边形内角和 三角形内角和
转化
A
B
C
D
四边形的内角和
A
D
C
B
结论:四边形的内角和为360o
∠A+∠B+∠C+∠D=360o
B
A
C
D
E
探究1
5边形内角和=3×180°=540°
多边形边数
图形
从多边形的一个顶点引出的对角线条数
分割出三角形的个数
多边形内角和
三角形
(n=3)
四边形
(n=4)
五边形
(n=5)
六边形
(n=6)
n边形
······
······
······
······
······
0
3 -3 =
4 -3 =
5 -3 =
6 -3 =
n-3
1
2
3
3 -2 =
1
4 -2 =
2
5 -2=
3
6 -2 =
4
n-2
(n-2)·180
180
360
540
720
结论:n边形内角和公式为:_________。
B
A
C
D
G
F
E
(n-2)·180°
①n代表什么?
② n-2表示什么含义?
③为什么要乘以180°
应用新知
1、求八边形的内角和的度数。
解:八边形的内角和是
(n-2)×1800
= (8-2)×1800
= 10800
答:八边形的内角和的度数是1080o。
2、一个多边形内角和等于1260°,它是几边形?
解:设它是n边形,根据题意,得
(n-2)· 180= 1260
解得 n =9
所以它是九边形。
3.求下列图形中x的值:
∟
(1)
∟
(2)
(3)
C
A
B
D
E
(4)
AB∥CD
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?
D
A
B
C
解: 如右图,四边形ABCD中,
∠A+∠C=180°.
∵ ∠A+∠B+∠C+∠D
=(4-2) ×180°
=360 °
∴ ∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补.
布置作业:
习题7.3 5 、7 、 8
感悟与收获
这堂课你收获了什么?
把一个多边形分成几个三角形,还有其他分法吗?由新的分法能得出多边形内角和公式吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °= (n-2)×180 °
