1.3 探索三角形全等的条件 同步练习(含答案)
文档属性
| 名称 | 1.3 探索三角形全等的条件 同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-27 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一章 三角形
3 探索三角形全等的条件
知识能力全练
知识点一 用“边边边(Sss)”判定两个三角形全等
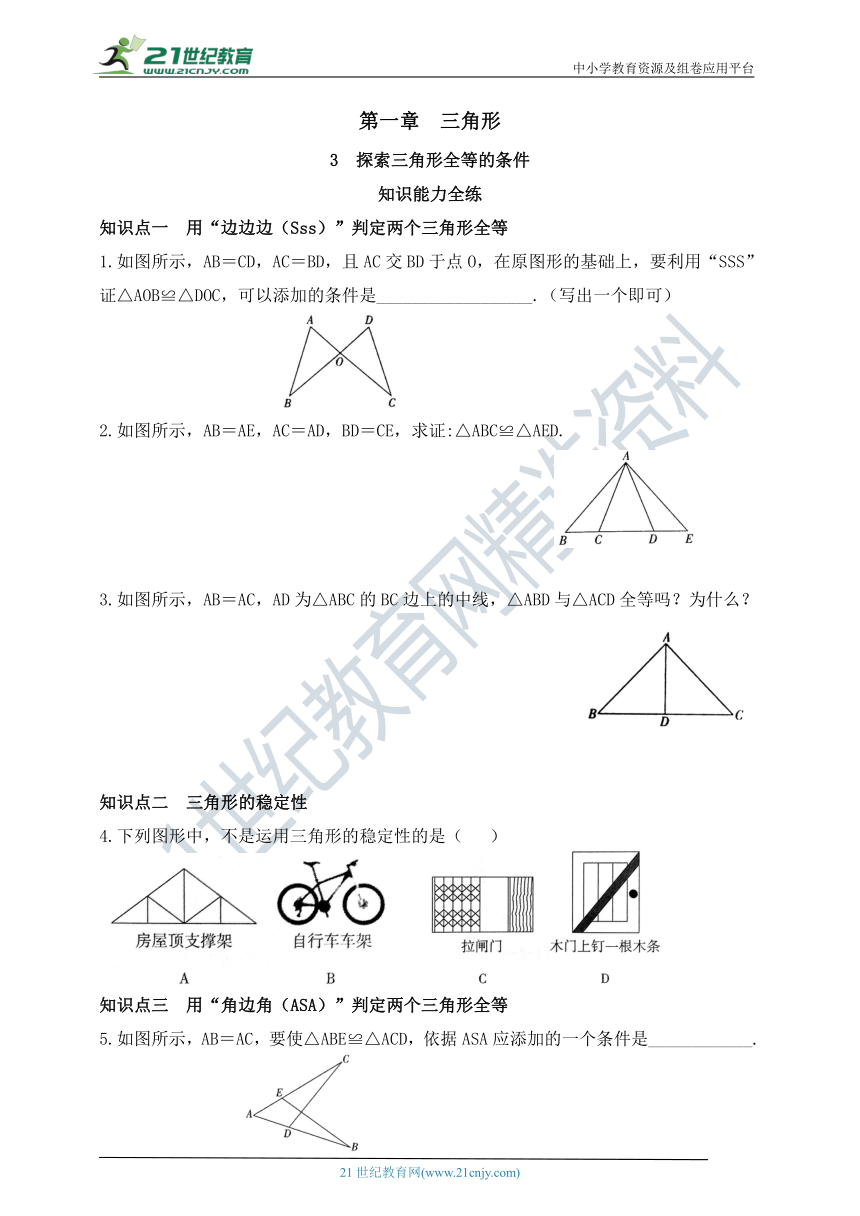
1.如图所示,AB=CD,AC=BD,且AC交BD于点O,在原图形的基础上,要利用“SSS”证△AOB≌△DOC,可以添加的条件是__________________.(写出一个即可)
2.如图所示,AB=AE,AC=AD,BD=CE,求证:△ABC≌△AED.
3.如图所示,AB=AC,AD为△ABC的BC边上的中线,△ABD与△ACD全等吗?为什么?
知识点二 三角形的稳定性
4.下列图形中,不是运用三角形的稳定性的是( )
知识点三 用“角边角(ASA)”判定两个三角形全等
5.如图所示,AB=AC,要使△ABE≌△ACD,依据ASA应添加的一个条件是____________.
6.如图所示,在△ABC中,AB=AC、AD⊥BC于点D,CE⊥AB于点E,AE=CE,AD与CE相交于点F.求证:△AEF≌△CEB.
7.如图所示,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC,求证:△ABD≌△EDC.
知识点四 用“角角边(AAS)”判定两个三角形全等
8.如图所示,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,求证:AB=DC.
9.如图所示,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与线段AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.
(1)线段BF与图中现有的哪一条线段相等?你得出的结论是BF=___________;
(2)证明你的结论.
知识点五 用“边角边(SAS)”判定两三角形全等
10.已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:
∠E=∠C.
11.已知:如图所示,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.求证:∠BED=∠C.
知识点六 三角形全等条件的灵活选用
12.如图所示,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
13.如图所示,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,D在BM上,△ABC和△ABD不全等,这个试验说明_______________________________________.
巩固提高全练
14.给出下列四组条件:
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.
其中能使△ABC≌△DEF的共有( )
A.1组 B.2组 C.3组 D.4组
15.如图所示,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4 m,Q点从B向D运动,每分钟走2 m,P点从B向A运动,PQ两点同时出发,P点每分钟走________m时,△CAP与△PQB全等.
16.如图所示,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2求证:
(1)△ABE≌△CBD;
(2)∠1=∠3.
17.如图所示,在△ABC中,∠ABC=∠ACB,BE=CF,E为BC边上一点,以E为顶点作∠AEF,∠AEF的一边交AC于点F,使∠AEF=∠B,请猜想AC与EC之间有怎样的数量关系,并说明理由.
18.如图所示,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
19.如图所示,已知∠ABC=∠DCB、添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,其中不能判定△ABC≌△DCB的是____________.(只填序号)
20.如图所示,CA平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为____________.
21.如图所示,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
22.如图所示,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
23.如图①,△ABC中,H是高AD和高BE的交点,且AD=BD.
(1)请你猜想BH和AC的数量关系,并说明理由;
(2)若将图①中的∠BAC改成钝角,请你在图②中画出该题的图形,此时(1)中的结论还成立吗?
参考答案
1.0A=OD(或OB=0C)
2.证明:∵BD=CE,∴BC=DE.
在△ABC和△AED中,∵AB=AE, AC=AD, BC=DE,∴△ABC≌△AED(SSS).
3.全等,理由如下:
∵AD为△ABC的BC边上的中线,∴BD=CD,
在△ABD与△ACD中,∴△ABD≌△ACD(SSS).
4.C 5.∠B=∠C
6.证明:∵AD⊥BC,∴∠B+∠BAD=90°,
∵CE⊥AB,∴∠BEC=∠FEA=90°,∴∠B+∠BCE=90°,∴∠EAF=∠ECB,
在△AEF和△CEB中,∴△AEF≌△CEB(ASA).
7.证明:∵AB∥CD,∴∠ABD=∠EDC,
在△ABD和△EDC中,∴△ABD≌△EDC(ASA).
8.证明:∵点E,F在BC上,BE=CF,∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,∴△ABF≌△DCE(AAS).∴AB=DC.
9.解析(1)AE.
(2)证明:∵CF⊥BE,∴∠BFC=90°,∴∠A=∠BFC,
∵AD∥BC,∴∠AEB=∠FBC,
由题意,得BE=BC,
在△AEB和△FBC中,∴△AEB≌△FBC(AAS),∴BF=AE.
10.证明:∵∠BAE=∠DAC,∴∠BAE+∠CAE=∠DAC+∠CAE,
∴∠CAB=∠EAD,又∵AB=AD,AC=AE,∴△ABC≌△ADE(SAS),∴∠C=∠E.
11.证明:∵AD⊥BC∴∠BDE=∠ADC=90°.
在△BDE和△ADC中,∴△BDE≌△ADC(SAS),∴∠BED=∠C.
12.C
13.有两边和其中一边的对角分别相等的两个三角形不一定全等
14.C 15.1或3
16.证明 (1)∵∠1=∠2,∴∠1+∠CBE=∠2+∠CBE,即∠ABE=∠CBD.
在△ABE和△CBD中,∴△ABE≌△CBD(SAS).
(2)∵△ABE≌△CBD,∴∠A=∠C.
∵∠AFB=∠CFE,∴∠1=∠3.
17.AC=EC,理由如下:
∵∠ABC=∠ACB,∴AB=AC,
∥∠BEA+∠B+∠BAE=180°,∠BEA+∠AEF+∠CEF=180°,
∴∠B+∠BAE=∠AEF+∠CEF,
又∵∠AEF=∠B,∴∠BAE=∠CEF,
在△ABE和△ECF中,∴△ABE≌△ECF(AAS),∴AB=EC.
又∵AB=AC,∴AC=EC.
18.B 19.② 20.82°
21.证明: ∵DE∥AC,∴∠EDB=∠A.
在△DEB与△ABC中,∴△DEB≌△ABC(SAS).
22.解析(1)证明:在△BEF和△CDA中,
∴△BEF≌△CDA(SAS),∴∠D=∠2.
(2)∵∠D=∠2,∠D=78°,∴∠2=78°,
∵EF∥AC,∴∠BAC=∠2=78°.
23.(1)BH=AC.
理由:∵AD和BE是△ABC的高,
∴∠BDH=∠ADC=90°,∠DBH+∠C=∠CAD+∠C=90°,∴∠DBH=∠DAC,
在△BDH和△ADC中,∴△BDH≌△ADC(ASA),∴BH=AC.
(2)成立如图,
∵AD和BE是△ABC的高,∴∠BDH=∠ADC=∠BEC=90°,
∴∠DBH+∠H=∠DBH+∠C=90°,∴∠H=∠C,
在△BDH和△ADC中,∴△BDH≌△ADC(AAS),∴BH=AC.
_21?????????è?????(www.21cnjy.com)_
第一章 三角形
3 探索三角形全等的条件
知识能力全练
知识点一 用“边边边(Sss)”判定两个三角形全等
1.如图所示,AB=CD,AC=BD,且AC交BD于点O,在原图形的基础上,要利用“SSS”证△AOB≌△DOC,可以添加的条件是__________________.(写出一个即可)
2.如图所示,AB=AE,AC=AD,BD=CE,求证:△ABC≌△AED.
3.如图所示,AB=AC,AD为△ABC的BC边上的中线,△ABD与△ACD全等吗?为什么?
知识点二 三角形的稳定性
4.下列图形中,不是运用三角形的稳定性的是( )
知识点三 用“角边角(ASA)”判定两个三角形全等
5.如图所示,AB=AC,要使△ABE≌△ACD,依据ASA应添加的一个条件是____________.
6.如图所示,在△ABC中,AB=AC、AD⊥BC于点D,CE⊥AB于点E,AE=CE,AD与CE相交于点F.求证:△AEF≌△CEB.
7.如图所示,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC,求证:△ABD≌△EDC.
知识点四 用“角角边(AAS)”判定两个三角形全等
8.如图所示,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,求证:AB=DC.
9.如图所示,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与线段AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.
(1)线段BF与图中现有的哪一条线段相等?你得出的结论是BF=___________;
(2)证明你的结论.
知识点五 用“边角边(SAS)”判定两三角形全等
10.已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:
∠E=∠C.
11.已知:如图所示,在△ABC中,AD⊥BC,垂足是D,E是线段AD上的点,且AD=BD,DE=DC.求证:∠BED=∠C.
知识点六 三角形全等条件的灵活选用
12.如图所示,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
13.如图所示,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,D在BM上,△ABC和△ABD不全等,这个试验说明_______________________________________.
巩固提高全练
14.给出下列四组条件:
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.
其中能使△ABC≌△DEF的共有( )
A.1组 B.2组 C.3组 D.4组
15.如图所示,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4 m,Q点从B向D运动,每分钟走2 m,P点从B向A运动,PQ两点同时出发,P点每分钟走________m时,△CAP与△PQB全等.
16.如图所示,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2求证:
(1)△ABE≌△CBD;
(2)∠1=∠3.
17.如图所示,在△ABC中,∠ABC=∠ACB,BE=CF,E为BC边上一点,以E为顶点作∠AEF,∠AEF的一边交AC于点F,使∠AEF=∠B,请猜想AC与EC之间有怎样的数量关系,并说明理由.
18.如图所示,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
19.如图所示,已知∠ABC=∠DCB、添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,其中不能判定△ABC≌△DCB的是____________.(只填序号)
20.如图所示,CA平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为____________.
21.如图所示,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
22.如图所示,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
23.如图①,△ABC中,H是高AD和高BE的交点,且AD=BD.
(1)请你猜想BH和AC的数量关系,并说明理由;
(2)若将图①中的∠BAC改成钝角,请你在图②中画出该题的图形,此时(1)中的结论还成立吗?
参考答案
1.0A=OD(或OB=0C)
2.证明:∵BD=CE,∴BC=DE.
在△ABC和△AED中,∵AB=AE, AC=AD, BC=DE,∴△ABC≌△AED(SSS).
3.全等,理由如下:
∵AD为△ABC的BC边上的中线,∴BD=CD,
在△ABD与△ACD中,∴△ABD≌△ACD(SSS).
4.C 5.∠B=∠C
6.证明:∵AD⊥BC,∴∠B+∠BAD=90°,
∵CE⊥AB,∴∠BEC=∠FEA=90°,∴∠B+∠BCE=90°,∴∠EAF=∠ECB,
在△AEF和△CEB中,∴△AEF≌△CEB(ASA).
7.证明:∵AB∥CD,∴∠ABD=∠EDC,
在△ABD和△EDC中,∴△ABD≌△EDC(ASA).
8.证明:∵点E,F在BC上,BE=CF,∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,∴△ABF≌△DCE(AAS).∴AB=DC.
9.解析(1)AE.
(2)证明:∵CF⊥BE,∴∠BFC=90°,∴∠A=∠BFC,
∵AD∥BC,∴∠AEB=∠FBC,
由题意,得BE=BC,
在△AEB和△FBC中,∴△AEB≌△FBC(AAS),∴BF=AE.
10.证明:∵∠BAE=∠DAC,∴∠BAE+∠CAE=∠DAC+∠CAE,
∴∠CAB=∠EAD,又∵AB=AD,AC=AE,∴△ABC≌△ADE(SAS),∴∠C=∠E.
11.证明:∵AD⊥BC∴∠BDE=∠ADC=90°.
在△BDE和△ADC中,∴△BDE≌△ADC(SAS),∴∠BED=∠C.
12.C
13.有两边和其中一边的对角分别相等的两个三角形不一定全等
14.C 15.1或3
16.证明 (1)∵∠1=∠2,∴∠1+∠CBE=∠2+∠CBE,即∠ABE=∠CBD.
在△ABE和△CBD中,∴△ABE≌△CBD(SAS).
(2)∵△ABE≌△CBD,∴∠A=∠C.
∵∠AFB=∠CFE,∴∠1=∠3.
17.AC=EC,理由如下:
∵∠ABC=∠ACB,∴AB=AC,
∥∠BEA+∠B+∠BAE=180°,∠BEA+∠AEF+∠CEF=180°,
∴∠B+∠BAE=∠AEF+∠CEF,
又∵∠AEF=∠B,∴∠BAE=∠CEF,
在△ABE和△ECF中,∴△ABE≌△ECF(AAS),∴AB=EC.
又∵AB=AC,∴AC=EC.
18.B 19.② 20.82°
21.证明: ∵DE∥AC,∴∠EDB=∠A.
在△DEB与△ABC中,∴△DEB≌△ABC(SAS).
22.解析(1)证明:在△BEF和△CDA中,
∴△BEF≌△CDA(SAS),∴∠D=∠2.
(2)∵∠D=∠2,∠D=78°,∴∠2=78°,
∵EF∥AC,∴∠BAC=∠2=78°.
23.(1)BH=AC.
理由:∵AD和BE是△ABC的高,
∴∠BDH=∠ADC=90°,∠DBH+∠C=∠CAD+∠C=90°,∴∠DBH=∠DAC,
在△BDH和△ADC中,∴△BDH≌△ADC(ASA),∴BH=AC.
(2)成立如图,
∵AD和BE是△ABC的高,∴∠BDH=∠ADC=∠BEC=90°,
∴∠DBH+∠H=∠DBH+∠C=90°,∴∠H=∠C,
在△BDH和△ADC中,∴△BDH≌△ADC(AAS),∴BH=AC.
_21?????????è?????(www.21cnjy.com)_
