2021-2022学年鲁教五四新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 482.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-26 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教五四新版九年级上册数学《第1章
反比例函数》单元测试卷
一.选择题
1.如图,A、B是双曲线y=上关于原点对称的任意两点,AC∥y轴,BD∥y轴,则四边形ACBD的面积S满足( )
A.S=1
B.1<S<2
C.S=2
D.S>2
2.反比例函数的图象在第一、第三象限,则m可能取的一个值为( )
A.0
B.1
C.2
D.3
3.在反比例函数y=图象上的点是( )
A.(2,3)
B.(4,2)
C.(﹣6,1)
D.(﹣2,3)
4.下列关系式中,y是x的反比例函数的是( )
A.y=4x
B.=3
C.y=﹣
D.y=x2﹣1
5.已知函数y=kx中y随x的增大而减小,那么它和函数y=在同一直角坐标系内的大致图象可能是( )
A.
B.
C.
D.
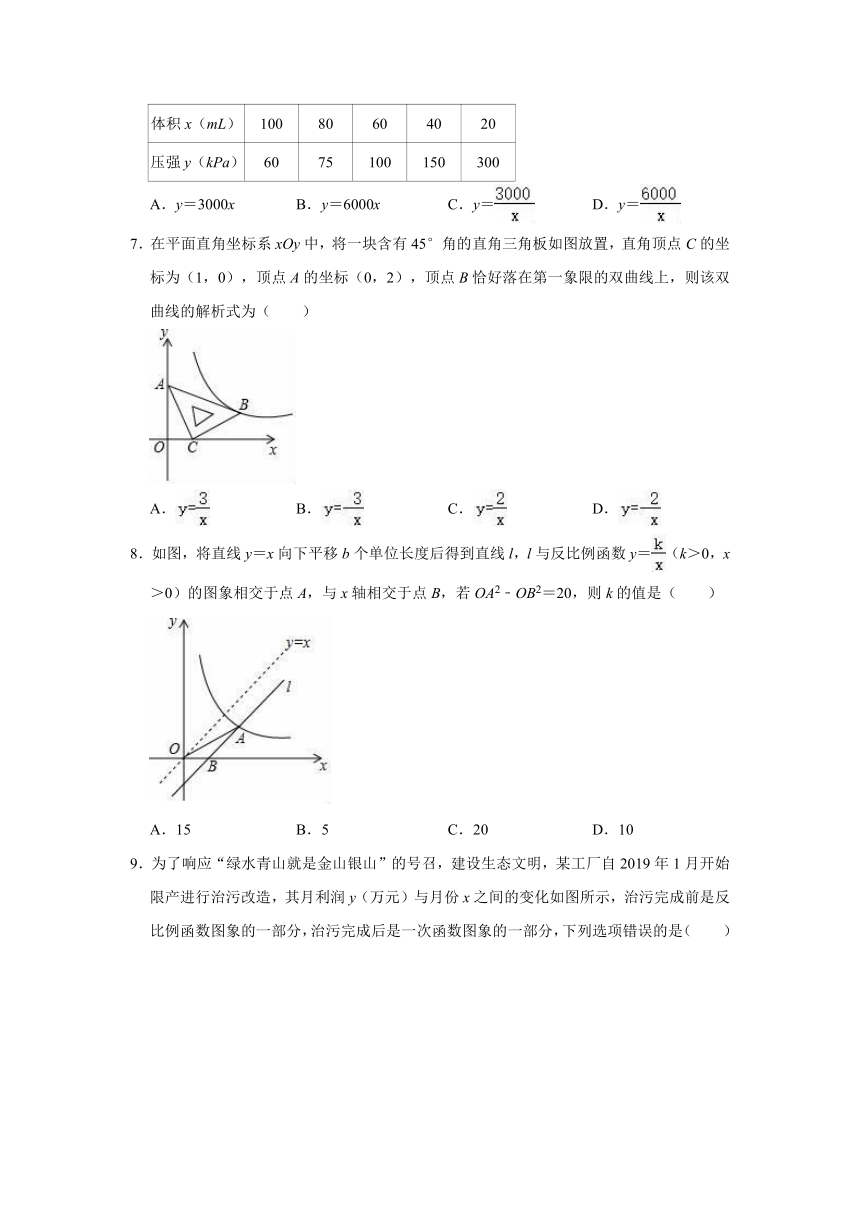
6.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积x(mL)
100
80
60
40
20
压强y(kPa)
60
75
100
150
300
A.y=3000x
B.y=6000x
C.y=
D.y=
7.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,则该双曲线的解析式为( )
A.
B.
C.
D.
8.如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=(k>0,x>0)的图象相交于点A,与x轴相交于点B,若OA2﹣OB2=20,则k的值是( )
A.15
B.5
C.20
D.10
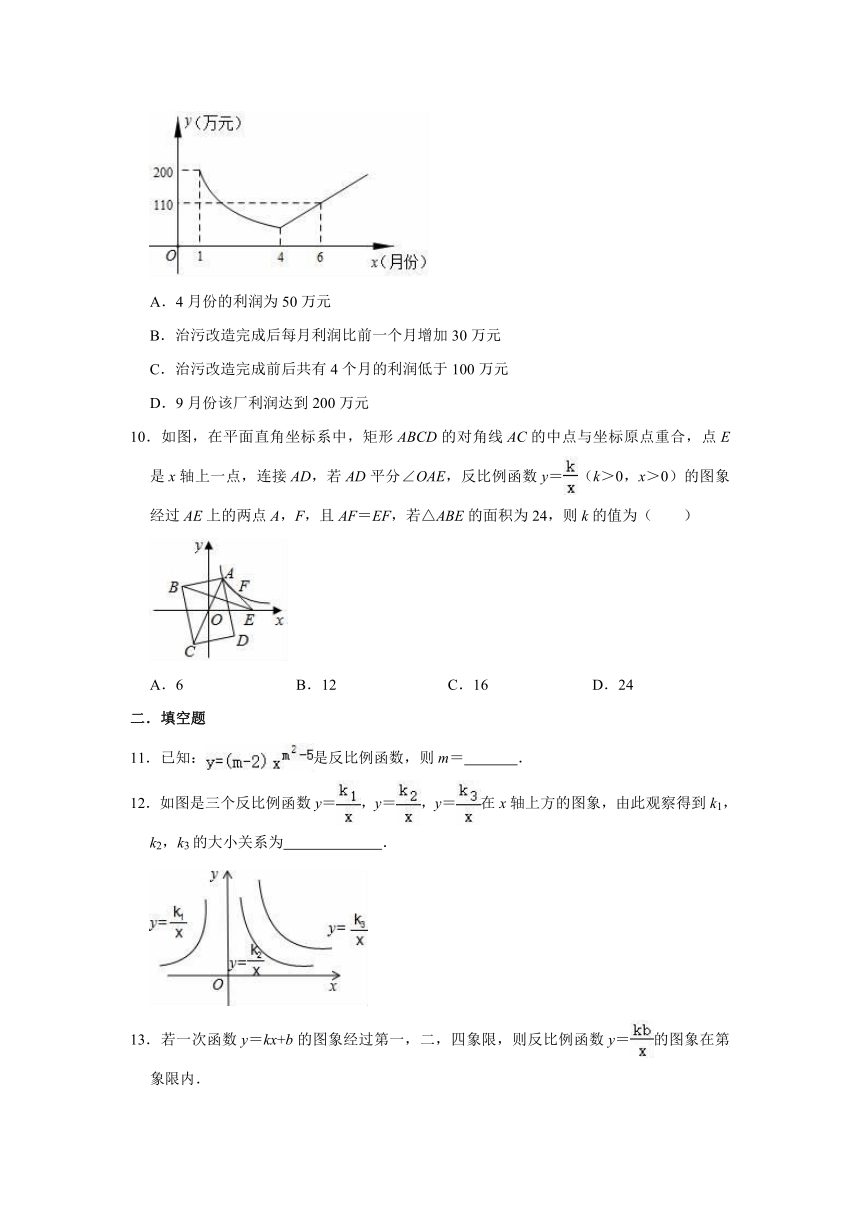
9.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
10.如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AD,若AD平分∠OAE,反比例函数y=(k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,若△ABE的面积为24,则k的值为( )
A.6
B.12
C.16
D.24
二.填空题
11.已知:是反比例函数,则m=
.
12.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为
.
13.若一次函数y=kx+b的图象经过第一,二,四象限,则反比例函数y=的图象在第
象限内.
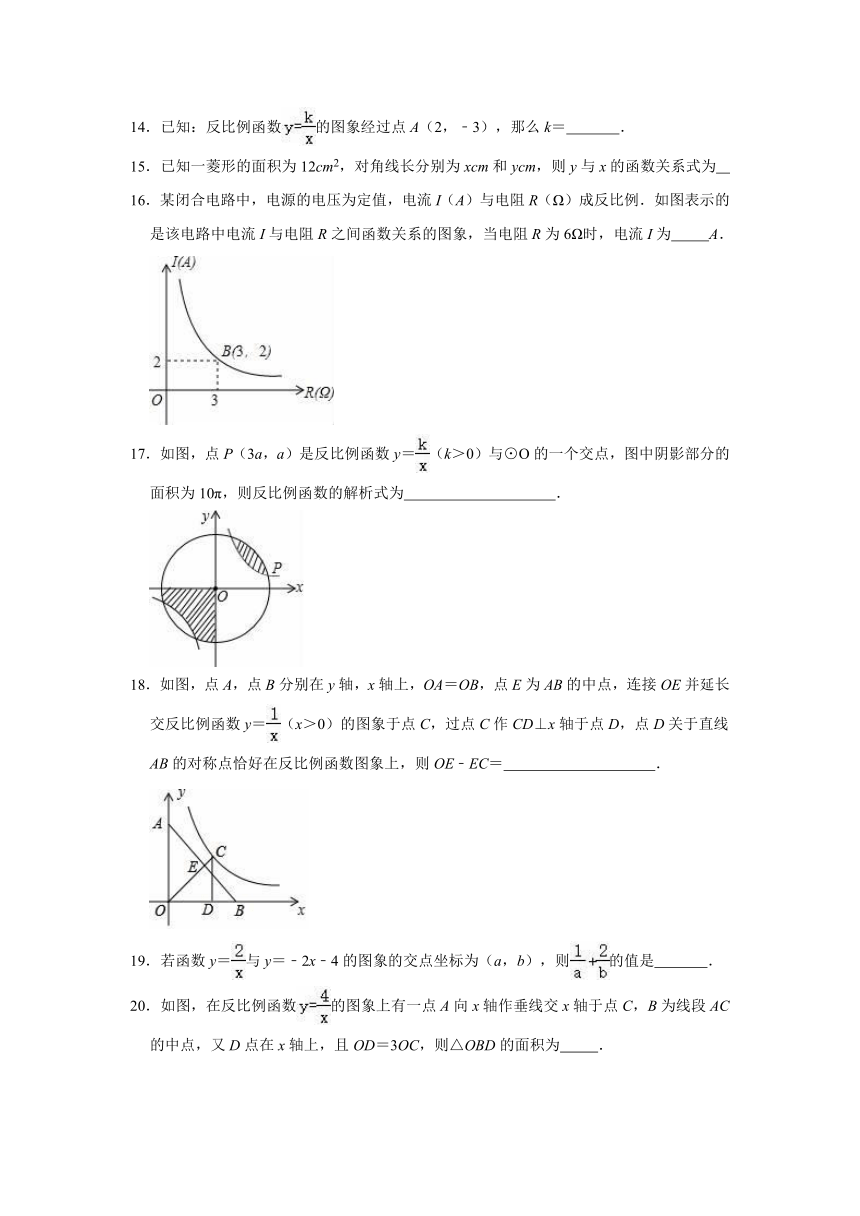
14.已知:反比例函数的图象经过点A(2,﹣3),那么k=
.
15.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
16.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图表示的是该电路中电流I与电阻R之间函数关系的图象,当电阻R为6Ω时,电流I为
A.
17.如图,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为
.
18.如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC=
.
19.若函数y=与y=﹣2x﹣4的图象的交点坐标为(a,b),则的值是
.
20.如图,在反比例函数的图象上有一点A向x轴作垂线交x轴于点C,B为线段AC的中点,又D点在x轴上,且OD=3OC,则△OBD的面积为
.
三.解答题
21.有这样一个问题:探究函数的图象与性质并解决问题.
小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数的自变量x的取值范围是x≠2;
(2)取几组y与x的对应值,填写在下表中.
x
…
﹣4
﹣2
﹣1
0
1
1.2
1.25
2.75
2.8
3
4
5
6
8
…
y
…
1
1.5
2
3
6
7.5
8
8
7.5
6
3
m
1.5
1
…
m的值为
;
(3)如图,在平面直角坐标系xOy中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数的图象是轴对称图形,它的对称轴是
;
②过点P(﹣1,n)(0<n<2)作直线l∥x轴,与函数的图象交于点M,N(点M在点N的左侧),则PN﹣PM的值为
.
22.如图,在平行四边形OABC中,OC=2,∠AOC=45°,点A在x轴上,点D是AB的中点,反比例函数y=(k>0,x>0)的图象经过C、D两点.
(1)求k的值;
(2)求点D的坐标.
23.已知函数是反比例函数,求k的值.
24.小明在学习过程中遇到了一个函数y=+1,小明根据学习反比例函数y=的经验,对函数y=+1的图象和性质进行了探究.
(1)画函数图象:[问题1]函数y=+1的自变量x的取值范围是
;
①列表:如表.
x
…
﹣6
﹣2
1
0
3
4
6
10
…
y
…
0
﹣3
﹣1
﹣7
9
5
3
2
…
②描点:点已描出,如图所示.
③连线:[问题2]请你根据描出的点,西出该函数的图象.
(2)探究性质:根据反比例函数y=的图象和性质,结合画出的函数y=+1图象,回答下列问题:
[问题3]①该函数的图象是具有轴对称性和中心对称性,其对称中心的坐标是
;
[问题4]②该函数图象可以看成是由y=的图象平移得到的,其平移方式为
;
[问题5]③结合函数图象,请直接写出+1≥﹣1时x的取值范围
.
25.如图,在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(4,),点B在y轴的负半轴上,AB交x轴于点C,C为线段AB的中点.
(1)m=
,点C的坐标为
;
(2)若点D为线段AB上的一个动点,过点D作DE∥y轴,交反比例函数图象于点E,求△ODE面积的最大值.
26.如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF=AD,求出点E的坐标.
参考答案与试题解析
一.选择题
1.解:∵A,B是函数y=的图象上关于原点O对称的任意两点,且AC平行于y轴,BD平行于y轴,
∴S△AOC=S△BOD=,
假设A点坐标为(x,y),则B点坐标为(﹣x,﹣y),
则OC=OD=x,
∴S△AOD=S△AOC=,S△BOC=S△BOD=,
∴四边形ABCD面积=S△AOD+S△AOC+S△BOC+S△BOD=×4=2.
故选:C.
2.解:∵反比例函数的图象在第一、第三象限,
∴1﹣m>0,
∴m<1,
符合条件的答案只有A,
故选:A.
3.解:∵2×3=6,4×2=8,﹣6×1=﹣6,﹣2×3=﹣6,
∴点(2,3)在反比例函数y=图象上,点(4,2),(﹣6,1),(﹣2,3)不在反比例函数y=图象上.
故选:A.
4.解:A、y=4x是正比例函数;
B、=3,可以化为y=3x,是正比例函数;
C、y=﹣是反比例函数;
D、y=x2﹣1是二次函数;
故选:C.
5.解:∵函数y=kx中y随x的增大而减小,
∴k<0,
∴函数y=kx的图象经过二、四象限,故可排除A、B;
∵k<0,
∴函数y=的图象在二、四象限,故C错误,D正确.
故选:D.
6.解:由表格数据可得:此函数是反比例函数,设解析式为:y=,
则xy=k=6000,
故y与x之间的关系的式子是y=,
故选:D.
7.解:过点B作BD⊥x轴于点D,
∵∠ACO+∠BCD=90°,
∠OAC+∠ACO=90°,
∴∠OAC=∠BCD,
在△ACO与△BCD中,
,
∴△ACO≌△BCD(AAS)
∴OC=BD,OA=CD,
∵A(0,2),C(1,0)
∴OD=3,BD=1,
∴B(3,1),
∴设反比例函数的解析式为y=,
将B(3,1)代入y=,
∴k=3,
∴该双曲线的解析式为y=,
故选:A.
8.解:直线y=x向下平移b个单位后得直线l:y=x﹣b,
∴B(b,0),
∵l与反比例函数y=(k>0,x>0)的图象相交于点A,
∴x﹣b=,则x2﹣bx﹣k=0.
∴x2=bx+k.
设点A的坐标为(x,x﹣b),
∵OA2﹣OB2=x2+(x﹣b)2﹣b2=2x2﹣2bx=2(bx+k)﹣2bx=2k,OA2﹣OB2=20,
∴2k=20,
∴k=10.
故选:D.
9.解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
10.解:连接BD,
∵四边形ABCD为矩形,
∴O为对角线AC,BD交点,OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠OAE,
∴∠OAD=∠EAD,
∴∠ODA=∠EAD,
∴BD∥AE,
∴S△ABE=S△AOE=24.
设点A坐标为(m,),
∵AF=EF,即F为AE中点,
∴点F纵坐标为,
将y=代入y=得x=2m,
∴点F坐标为(2m,),
∴点E横坐标为2×2m﹣m=3m,
即点E坐标为(3m,0).
∴S△AOE=OE?yA=×3m×=24,
解得k=16.
故选:C.
二.填空题
11.解:因为是反比例函数,
所以x的指数m2﹣5=﹣1,
即m2=4,解得:m=2或﹣2;
又m﹣2≠0,
所以m≠2,即m=﹣2.
故答案为:﹣2.
12.解:读图可知:三个反比例函数y=的图象在第二象限;故k1<0;y=,y=在第一象限;且y=的图象距原点较远,故有:k1<k2<k3;综合可得:k1<k2<k3.故填k1<k2<k3.
13.解:y=kx+b的图象经过第一、二、四象限,
则k<0,b>0,
得kb<0,
所以y=的图象在第二、四象限.
14.解:根据题意,得
﹣3=,
解得,k=﹣6.
故答案是:﹣6.
15.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
16.解:设I=,那么点(3,2)适合这个函数解析式,则k=3×2=6,
∴I=.
令R=6,
解得:I==1.
故答案为1.
17.解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:
πr2=10π
解得:r=2.
∵点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点.
∴3a2=k.
=r
∴a2=×(2)2=4.
∴k=3×4=12,
则反比例函数的解析式是:y=.
故答案是:y=.
18.解:∵点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,
∴直线OC的解析式为y=x,
设C(a,a),
∵点C在反比例函数y=(x>0)的图象上,
∴a2=1,
∴a=1,
∴C(1,1),
∴D(1,0),
∴设直线AB的解析式为y=﹣x+b,则B(b,0),BD=b﹣1.
∵点D和点F关于直线AB对称,
∴BF=BD=b﹣1,
∴F(b,b﹣1),
∵F在反比例函数y=的图象上,
∴b(b﹣1)=1,
解得b1=,b2=(舍去),
∴B(,0),
∵C(1,1),
∴OD=CD=1,
∴OC=,
易证△ODC∽△OEB,
∴=,即=,
∴OE=,
∴OE﹣EC=OE﹣(OC﹣OE)=2OE﹣OC=﹣=.
故答案为:.
19.解:联立两个函数表达式得,
整理得:x2+2x+1=0,
解得:x=﹣1,
∴y=﹣2,
交点坐标是(﹣1,﹣2),
∴a=﹣1,b=﹣2,
则=﹣1﹣1=﹣2.
故答案为﹣2.
20.解:设A(x、y),由反比例函数可知xy=4,
BC=AC=y,OD=3OC=3x,
∴S△OBD=BC×OD=×y×3x=xy=×4=3.
故答案为:3.
三.解答题
21.解:(2)由题意x=5时,y==2,
∴m=2,
故答案为2.
(3)函数图象如图所示:
(4)①观察图象可知图象是轴对称图形,对称轴x=2.
故答案为x=2.
②由题意,M(﹣+2,n),N(+2,n),
∴PN=+2+1=+3,PM=﹣1﹣(﹣+2)=﹣3,
∴PN﹣PM=+3﹣(﹣3)=6,
故答案为6.
22.解:(1)过C作CE⊥OA于E,
∵OC=2,∠AOC=45°,
∴OE=OC=sin45°×2=2,
∴C(2,2),
∵反比例函数y=(k>0,x>0)的图象经过C,
∴k=2×2=4,
(2)作DF⊥OA于F,
由平行四边形OABC可知:BC∥OA,
∴B的纵坐标等于C的纵坐标2,
∴DF=1,
∵反比例函数y=(k>0,x>0)的图象经过D,
∴1=,
∴x=4,
∴D(4,1).
23.解:∵是反比例函数,
∴k2﹣k﹣3=﹣1且k﹣2≠0,
解得:k=﹣1.
24.解:(1)函数y=+1的自变量x的取值范围是:x≠2,
故答案为:x≠2;
如图所示,
(2)根据反比例函数y=的图象和性质,结合画出的函数y=+1图象可知:
①该函数的图象是具有轴对称性和中心对称性,其对称中心的坐标是
(2,1);
②该函数图象可以看成是由y=的图象平移得到的,其平移方式为:向右平移2个单位,再向上平移1个单位;
③结合函数图象,
+1≥﹣1时x的取值范围是x≤0或x>2.
故答案为(2,1);向右平移2个单位,再向上平移1个单位;x≤0或x>2.
25.解:(1)∵反比例函数y=(x>0)的图象经过点A(4,),
∴m==6,
∵AB交x轴于点C,C为线段AB的中点.
∴C(2,0);
故答案为6,(2,0);
(2)设直线AB的解析式为y=kx+b,
把A(4,),C(2,0)代入得,解得,
∴直线AB的解析式为y=x﹣;
∵点D为线段AB上的一个动点,
∴设D(x,
x﹣)(0<x≤4),
∵DE∥y轴,
∴E(x,),
∴S△ODE=x?(﹣x+)=﹣x2+x+3=﹣(x﹣1)2+,
∴当x=1时,△ODE的面积的最大值为.
26.解:(1)设反比例函数的解析式为y=,
把(n,1)代入得:k=n,
即y=,
∵点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5,
∴,
解得:m=1,n=6,
即A(1,6),B(6,1);
反比例函数的解析式为:y=;
(2)设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入得:,
解得:a=﹣1,b=7,
即直线AB的解析式为:y=﹣x+7,
设E点的横坐标为m,则E(m,﹣m+7),F(m,),
∴EF=﹣m+7﹣,
∵EF=AD,
∴﹣m+7﹣=,
解得:m1=2,m2=3,
经检验都是原方程的解,
即E的坐标为(2,5)或(3,4).
反比例函数》单元测试卷
一.选择题
1.如图,A、B是双曲线y=上关于原点对称的任意两点,AC∥y轴,BD∥y轴,则四边形ACBD的面积S满足( )
A.S=1
B.1<S<2
C.S=2
D.S>2
2.反比例函数的图象在第一、第三象限,则m可能取的一个值为( )
A.0
B.1
C.2
D.3
3.在反比例函数y=图象上的点是( )
A.(2,3)
B.(4,2)
C.(﹣6,1)
D.(﹣2,3)
4.下列关系式中,y是x的反比例函数的是( )
A.y=4x
B.=3
C.y=﹣
D.y=x2﹣1
5.已知函数y=kx中y随x的增大而减小,那么它和函数y=在同一直角坐标系内的大致图象可能是( )
A.
B.
C.
D.
6.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积x(mL)
100
80
60
40
20
压强y(kPa)
60
75
100
150
300
A.y=3000x
B.y=6000x
C.y=
D.y=
7.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,则该双曲线的解析式为( )
A.
B.
C.
D.
8.如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=(k>0,x>0)的图象相交于点A,与x轴相交于点B,若OA2﹣OB2=20,则k的值是( )
A.15
B.5
C.20
D.10
9.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
10.如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AD,若AD平分∠OAE,反比例函数y=(k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,若△ABE的面积为24,则k的值为( )
A.6
B.12
C.16
D.24
二.填空题
11.已知:是反比例函数,则m=
.
12.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为
.
13.若一次函数y=kx+b的图象经过第一,二,四象限,则反比例函数y=的图象在第
象限内.
14.已知:反比例函数的图象经过点A(2,﹣3),那么k=
.
15.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
16.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图表示的是该电路中电流I与电阻R之间函数关系的图象,当电阻R为6Ω时,电流I为
A.
17.如图,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为
.
18.如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC=
.
19.若函数y=与y=﹣2x﹣4的图象的交点坐标为(a,b),则的值是
.
20.如图,在反比例函数的图象上有一点A向x轴作垂线交x轴于点C,B为线段AC的中点,又D点在x轴上,且OD=3OC,则△OBD的面积为
.
三.解答题
21.有这样一个问题:探究函数的图象与性质并解决问题.
小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数的自变量x的取值范围是x≠2;
(2)取几组y与x的对应值,填写在下表中.
x
…
﹣4
﹣2
﹣1
0
1
1.2
1.25
2.75
2.8
3
4
5
6
8
…
y
…
1
1.5
2
3
6
7.5
8
8
7.5
6
3
m
1.5
1
…
m的值为
;
(3)如图,在平面直角坐标系xOy中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数的图象是轴对称图形,它的对称轴是
;
②过点P(﹣1,n)(0<n<2)作直线l∥x轴,与函数的图象交于点M,N(点M在点N的左侧),则PN﹣PM的值为
.
22.如图,在平行四边形OABC中,OC=2,∠AOC=45°,点A在x轴上,点D是AB的中点,反比例函数y=(k>0,x>0)的图象经过C、D两点.
(1)求k的值;
(2)求点D的坐标.
23.已知函数是反比例函数,求k的值.
24.小明在学习过程中遇到了一个函数y=+1,小明根据学习反比例函数y=的经验,对函数y=+1的图象和性质进行了探究.
(1)画函数图象:[问题1]函数y=+1的自变量x的取值范围是
;
①列表:如表.
x
…
﹣6
﹣2
1
0
3
4
6
10
…
y
…
0
﹣3
﹣1
﹣7
9
5
3
2
…
②描点:点已描出,如图所示.
③连线:[问题2]请你根据描出的点,西出该函数的图象.
(2)探究性质:根据反比例函数y=的图象和性质,结合画出的函数y=+1图象,回答下列问题:
[问题3]①该函数的图象是具有轴对称性和中心对称性,其对称中心的坐标是
;
[问题4]②该函数图象可以看成是由y=的图象平移得到的,其平移方式为
;
[问题5]③结合函数图象,请直接写出+1≥﹣1时x的取值范围
.
25.如图,在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(4,),点B在y轴的负半轴上,AB交x轴于点C,C为线段AB的中点.
(1)m=
,点C的坐标为
;
(2)若点D为线段AB上的一个动点,过点D作DE∥y轴,交反比例函数图象于点E,求△ODE面积的最大值.
26.如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF=AD,求出点E的坐标.
参考答案与试题解析
一.选择题
1.解:∵A,B是函数y=的图象上关于原点O对称的任意两点,且AC平行于y轴,BD平行于y轴,
∴S△AOC=S△BOD=,
假设A点坐标为(x,y),则B点坐标为(﹣x,﹣y),
则OC=OD=x,
∴S△AOD=S△AOC=,S△BOC=S△BOD=,
∴四边形ABCD面积=S△AOD+S△AOC+S△BOC+S△BOD=×4=2.
故选:C.
2.解:∵反比例函数的图象在第一、第三象限,
∴1﹣m>0,
∴m<1,
符合条件的答案只有A,
故选:A.
3.解:∵2×3=6,4×2=8,﹣6×1=﹣6,﹣2×3=﹣6,
∴点(2,3)在反比例函数y=图象上,点(4,2),(﹣6,1),(﹣2,3)不在反比例函数y=图象上.
故选:A.
4.解:A、y=4x是正比例函数;
B、=3,可以化为y=3x,是正比例函数;
C、y=﹣是反比例函数;
D、y=x2﹣1是二次函数;
故选:C.
5.解:∵函数y=kx中y随x的增大而减小,
∴k<0,
∴函数y=kx的图象经过二、四象限,故可排除A、B;
∵k<0,
∴函数y=的图象在二、四象限,故C错误,D正确.
故选:D.
6.解:由表格数据可得:此函数是反比例函数,设解析式为:y=,
则xy=k=6000,
故y与x之间的关系的式子是y=,
故选:D.
7.解:过点B作BD⊥x轴于点D,
∵∠ACO+∠BCD=90°,
∠OAC+∠ACO=90°,
∴∠OAC=∠BCD,
在△ACO与△BCD中,
,
∴△ACO≌△BCD(AAS)
∴OC=BD,OA=CD,
∵A(0,2),C(1,0)
∴OD=3,BD=1,
∴B(3,1),
∴设反比例函数的解析式为y=,
将B(3,1)代入y=,
∴k=3,
∴该双曲线的解析式为y=,
故选:A.
8.解:直线y=x向下平移b个单位后得直线l:y=x﹣b,
∴B(b,0),
∵l与反比例函数y=(k>0,x>0)的图象相交于点A,
∴x﹣b=,则x2﹣bx﹣k=0.
∴x2=bx+k.
设点A的坐标为(x,x﹣b),
∵OA2﹣OB2=x2+(x﹣b)2﹣b2=2x2﹣2bx=2(bx+k)﹣2bx=2k,OA2﹣OB2=20,
∴2k=20,
∴k=10.
故选:D.
9.解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
10.解:连接BD,
∵四边形ABCD为矩形,
∴O为对角线AC,BD交点,OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠OAE,
∴∠OAD=∠EAD,
∴∠ODA=∠EAD,
∴BD∥AE,
∴S△ABE=S△AOE=24.
设点A坐标为(m,),
∵AF=EF,即F为AE中点,
∴点F纵坐标为,
将y=代入y=得x=2m,
∴点F坐标为(2m,),
∴点E横坐标为2×2m﹣m=3m,
即点E坐标为(3m,0).
∴S△AOE=OE?yA=×3m×=24,
解得k=16.
故选:C.
二.填空题
11.解:因为是反比例函数,
所以x的指数m2﹣5=﹣1,
即m2=4,解得:m=2或﹣2;
又m﹣2≠0,
所以m≠2,即m=﹣2.
故答案为:﹣2.
12.解:读图可知:三个反比例函数y=的图象在第二象限;故k1<0;y=,y=在第一象限;且y=的图象距原点较远,故有:k1<k2<k3;综合可得:k1<k2<k3.故填k1<k2<k3.
13.解:y=kx+b的图象经过第一、二、四象限,
则k<0,b>0,
得kb<0,
所以y=的图象在第二、四象限.
14.解:根据题意,得
﹣3=,
解得,k=﹣6.
故答案是:﹣6.
15.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
16.解:设I=,那么点(3,2)适合这个函数解析式,则k=3×2=6,
∴I=.
令R=6,
解得:I==1.
故答案为1.
17.解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:
πr2=10π
解得:r=2.
∵点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点.
∴3a2=k.
=r
∴a2=×(2)2=4.
∴k=3×4=12,
则反比例函数的解析式是:y=.
故答案是:y=.
18.解:∵点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,
∴直线OC的解析式为y=x,
设C(a,a),
∵点C在反比例函数y=(x>0)的图象上,
∴a2=1,
∴a=1,
∴C(1,1),
∴D(1,0),
∴设直线AB的解析式为y=﹣x+b,则B(b,0),BD=b﹣1.
∵点D和点F关于直线AB对称,
∴BF=BD=b﹣1,
∴F(b,b﹣1),
∵F在反比例函数y=的图象上,
∴b(b﹣1)=1,
解得b1=,b2=(舍去),
∴B(,0),
∵C(1,1),
∴OD=CD=1,
∴OC=,
易证△ODC∽△OEB,
∴=,即=,
∴OE=,
∴OE﹣EC=OE﹣(OC﹣OE)=2OE﹣OC=﹣=.
故答案为:.
19.解:联立两个函数表达式得,
整理得:x2+2x+1=0,
解得:x=﹣1,
∴y=﹣2,
交点坐标是(﹣1,﹣2),
∴a=﹣1,b=﹣2,
则=﹣1﹣1=﹣2.
故答案为﹣2.
20.解:设A(x、y),由反比例函数可知xy=4,
BC=AC=y,OD=3OC=3x,
∴S△OBD=BC×OD=×y×3x=xy=×4=3.
故答案为:3.
三.解答题
21.解:(2)由题意x=5时,y==2,
∴m=2,
故答案为2.
(3)函数图象如图所示:
(4)①观察图象可知图象是轴对称图形,对称轴x=2.
故答案为x=2.
②由题意,M(﹣+2,n),N(+2,n),
∴PN=+2+1=+3,PM=﹣1﹣(﹣+2)=﹣3,
∴PN﹣PM=+3﹣(﹣3)=6,
故答案为6.
22.解:(1)过C作CE⊥OA于E,
∵OC=2,∠AOC=45°,
∴OE=OC=sin45°×2=2,
∴C(2,2),
∵反比例函数y=(k>0,x>0)的图象经过C,
∴k=2×2=4,
(2)作DF⊥OA于F,
由平行四边形OABC可知:BC∥OA,
∴B的纵坐标等于C的纵坐标2,
∴DF=1,
∵反比例函数y=(k>0,x>0)的图象经过D,
∴1=,
∴x=4,
∴D(4,1).
23.解:∵是反比例函数,
∴k2﹣k﹣3=﹣1且k﹣2≠0,
解得:k=﹣1.
24.解:(1)函数y=+1的自变量x的取值范围是:x≠2,
故答案为:x≠2;
如图所示,
(2)根据反比例函数y=的图象和性质,结合画出的函数y=+1图象可知:
①该函数的图象是具有轴对称性和中心对称性,其对称中心的坐标是
(2,1);
②该函数图象可以看成是由y=的图象平移得到的,其平移方式为:向右平移2个单位,再向上平移1个单位;
③结合函数图象,
+1≥﹣1时x的取值范围是x≤0或x>2.
故答案为(2,1);向右平移2个单位,再向上平移1个单位;x≤0或x>2.
25.解:(1)∵反比例函数y=(x>0)的图象经过点A(4,),
∴m==6,
∵AB交x轴于点C,C为线段AB的中点.
∴C(2,0);
故答案为6,(2,0);
(2)设直线AB的解析式为y=kx+b,
把A(4,),C(2,0)代入得,解得,
∴直线AB的解析式为y=x﹣;
∵点D为线段AB上的一个动点,
∴设D(x,
x﹣)(0<x≤4),
∵DE∥y轴,
∴E(x,),
∴S△ODE=x?(﹣x+)=﹣x2+x+3=﹣(x﹣1)2+,
∴当x=1时,△ODE的面积的最大值为.
26.解:(1)设反比例函数的解析式为y=,
把(n,1)代入得:k=n,
即y=,
∵点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5,
∴,
解得:m=1,n=6,
即A(1,6),B(6,1);
反比例函数的解析式为:y=;
(2)设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入得:,
解得:a=﹣1,b=7,
即直线AB的解析式为:y=﹣x+7,
设E点的横坐标为m,则E(m,﹣m+7),F(m,),
∴EF=﹣m+7﹣,
∵EF=AD,
∴﹣m+7﹣=,
解得:m1=2,m2=3,
经检验都是原方程的解,
即E的坐标为(2,5)或(3,4).
