8.3简单几何体的表面积与体积-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案)
文档属性
| 名称 | 8.3简单几何体的表面积与体积-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 223.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 23:45:17 | ||
图片预览


文档简介
1285875-3028958.3简单几何体的表面积与体积
8.3简单几何体的表面积与体积
1.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,底面菱形的对角线的长分别是 214 和 102 ,则这个棱柱的侧面积是(???? )???????
A.?130??????????????????????????????????????B.?140??????????????????????????????????????C.?150??????????????????????????????????????D.?160
2.在三楼锥 P?ABC 中, D 为 BC 的中点, PA⊥ 底面 ABC , AB⊥AC , AB=4 , AC=2 ,若 PD 与底面 ABC 所成角为45°,则三棱锥 P?ABC 的体积为(??? )
A.?5?????????????????????????????????????B.?453?????????????????????????????????????C.?45?????????????????????????????????????D.?554
3.运用祖暅原理计算球的体积时,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆 x24+y29=1 绕 y 轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于(??? ).
A.?8π??????????????????????????????????????B.?16π??????????????????????????????????????C.?24π??????????????????????????????????????D.?32π
4.现有一批大小不同的球体原材料,某工厂要加工出一个四棱锥零件,要求零件底面 ABCD 为正方形, AB=2 ,侧面 △PAD 为等边三角形,线段 BC 的中点为 E ,若 PE=1 ,则所需球体原材料的最小体积为(??? )
A.?82π3???????????????????????????????????B.?28π3 C.?9π???????????????????????????????????D.?143π3
5.已知正方体 ABCD?A1B1C1D1 的棱长为a , 点 E,F,G 分别为棱 AB,AA1,C1D1 的中点,下列结论中正确的个数是( ??)
①过 E,F,G 三点作正方体的截面,所得截面为正六边形;② B1D1// 平面 EFG ;③异面直线 EF 与 BD1 所成角的正切值为 2 ;④四面体 ACB1D1 的体积等于等 a33 .
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
6.在直三棱柱 ABC?A1B1C1 中, AB=BC=2 , ∠ABC=π2 ,若该直三棱柱的外接球表面积为 16π ,则此直三棱柱的高为(? ??).
A.?4????????????????????????????????????????B.?3????????????????????????????????????????C.?42????????????????????????????????????????D.?22
7.已知四棱锥 P?ABCD 中,底面 ABCD 是矩形,侧面 PAD 是正三角形,且侧面 PAD⊥ 底面 ABCD , AB=2 ,若四棱锥 P?ABCD 外接球的体积为 82π3 ,则该四棱锥的表面积为(??? )
A.?43????????????????????????????????????B.?63????????????????????????????????????C.?83????????????????????????????????????D.?103
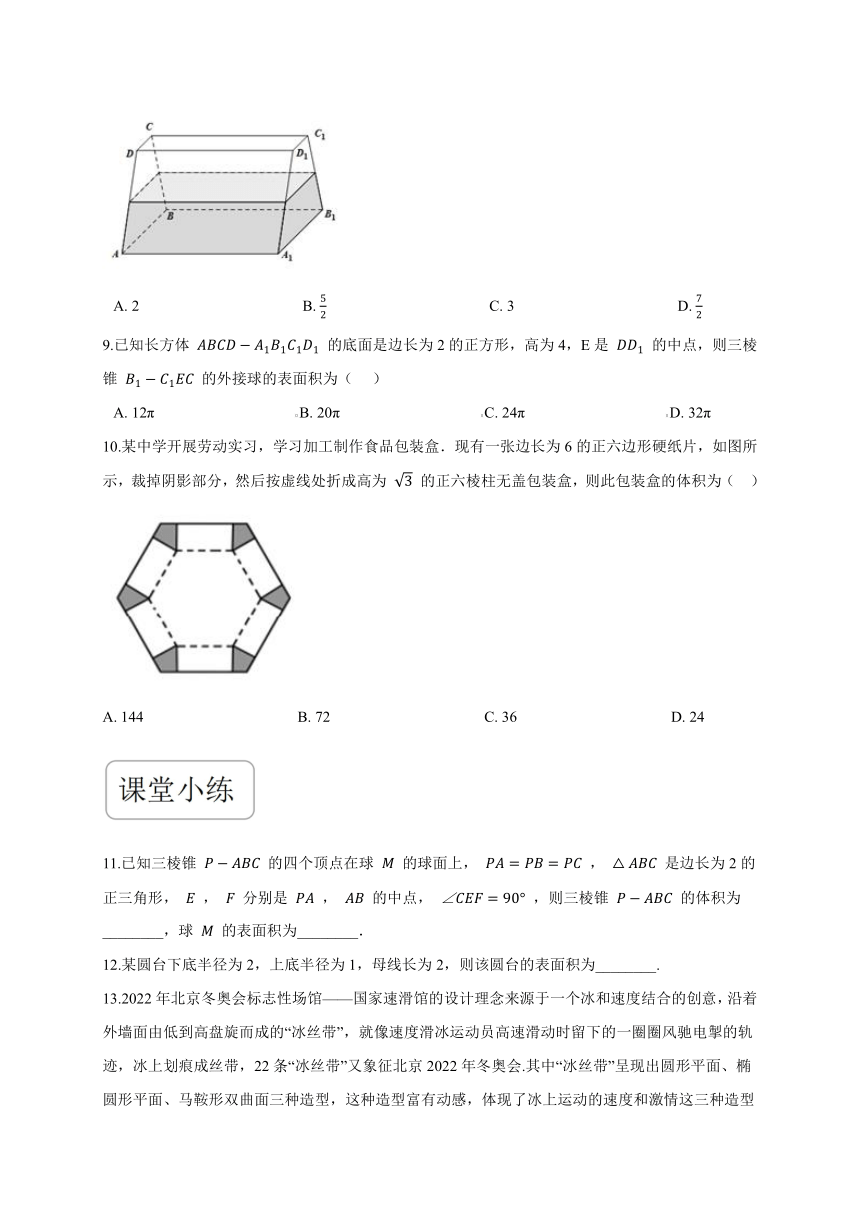
8.如图,一个四棱柱形容器中盛有水,在底面 ABCD 中, AB//CD , AB=3 , CD=1 ,侧棱 AA1=4 ,若侧面 AA1B1B 水平放置时,水面恰好过 AD,BC,B1C1,A1D1 的中点,那么当底面 ABCD 水平放置时,水面高为(??? )
A.?2???????????????????????????????????????????B.?52???????????????????????????????????????????C.?3???????????????????????????????????????????D.?72
9.已知长方体 ABCD?A1B1C1D1 的底面是边长为2的正方形,高为4,E是 DD1 的中点,则三棱锥 B1?C1EC 的外接球的表面积为(??? )
A.?12π?????????????????????????????????????B.?20π?????????????????????????????????????C.?24π?????????????????????????????????????D.?32π
10.某中学开展劳动实习,学习加工制作食品包装盒.现有一张边长为6的正六边形硬纸片,如图所示,裁掉阴影部分,然后按虚线处折成高为 3 的正六棱柱无盖包装盒,则此包装盒的体积为( ??)
A.?144????????????????????????????????????????B.?72????????????????????????????????????????C.?36????????????????????????????????????????D.?24
11.已知三棱锥 P?ABC 的四个顶点在球 M 的球面上, PA=PB=PC , △ABC 是边长为2的正三角形, E , F 分别是 PA , AB 的中点, ∠CEF=90° ,则三棱锥 P?ABC 的体积为________,球 M 的表面积为________.
12.某圆台下底半径为2,上底半径为1,母线长为2,则该圆台的表面积为________.
13.2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意,沿着外墙面由低到高盘旋而成的“冰丝带”,就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹,冰上划痕成丝带,22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型,这种造型富有动感,体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体,其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就,如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式,但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理:“幂势既同,则积不容异”,才利用牟合方盖的体积推导出球的体积公式原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
(Ⅰ)利用祖暅原理推导半径为 R 的球的体积公式时,可以构造如图②所示的几何体 M ,几何体 M 的底面半径和高都为 R ,其底面和半球体的底面同在平面 α 内.设与平面 α 平行且距离为 d 的平面 β 截两个几何体得到两个截面,请在图②中用阴影画出与图①中阴影截面面积相等的图形并给出证明;
(Ⅱ)现将椭圆 x2a2+y2b2=1(a>b>0) 所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球 A , B (如图),类比(Ⅰ)中的方法,探究椭球 A 的体积公式,并写出椭球 A , B 的体积之比.
14.长方体 ABCD?A1B1C1D1 中, AB =12, BC =10, AA1 =6,过 A1D1 作长方体的截面 A1D1EF 使它成为正方形,
(1)求截面 A1D1EF 将正方体分成的两部分的体积比;
(2)求 VB?A1D1EF
15.已知 ΔABC 的三边分别是 AC=3,BC=4,AB=5 ,以 AB 所在直线为轴将此三角形旋转一周,求所得旋转体的表面积
1.【答案】 D 2.【答案】 B 3.【答案】 B 4.【答案】 A 5.【答案】 B 6.【答案】 D 7.【答案】 B 8.【答案】 B 9.【答案】 B 10.【答案】 B
11.【答案】 23;6π 12.【答案】 11π
13.【答案】 解:(Ⅰ)由图可知,图①几何体的为半径为 R 的半球,图②几何体为底面半径和高都为 R 的圆柱中挖掉了一个圆锥,与图①截面面积相等的图形是圆环(如阴影部分)
证明如下:
在图①中,设截面圆的圆心为 O1 ,易得截面圆 O1 的面积为 π(R2?d2) ,
在图②中,截面截圆锥得到的小圆的半径为 d ,所以,圆环的面积为 π(R2?d2) ,所以,截得的截面的面积相等
(Ⅱ)类比(Ⅰ)可知,椭圆的长半轴为 a ,短半轴为 b ,构造一个底面半径为 b ,高为 a 的圆柱,把半椭球与圆柱放在同一个平面上(如图),在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,即挖去的圆锥底面半径为 b ,高为 a ;
在半椭球截面圆的面积 πb2a2(a2?d2) ,
在圆柱内圆环的面积为 πb2?πb2a2d2=πb2a2(a2?d2)
∴距离平面 α 为 d 的平面截取两个几何体的平面面积相等,
根据祖暅原理得出椭球 A 的体积为:
VA=2(V圆柱?V圆锥)=2(π?b2?a?13π?b2?a)=4π3ab2 ,
同理:椭球 B 的体积为 VB=4π3a2b
所以,两个椭球 A , B 的体积之比为 ba .
14.【答案】 (1)解: ∵ A1D1EF 是正方形, AB =12, BC =10, AA1 =6
∴ A1F=10 , AF=8 , BF=4
∵ 截面 A1D1EF 将正方体分成的两部分为三棱柱和四棱柱,且高 ? 相等均为长方体侧棱长
∴ VA1AF?D1DF=sA1AF? , VA1FBB1?D1ECC1=sA1FBB1?
∴VA1AF?D1DFVA1FBB1?D1ECC1=sA1AFsA1FBB1=12×8×6(12+4)×62=12
(2)解:过点B作直线BG平行于 A1F 交 A1B1 于点G,过G作 A1F 的垂线交 A1F 于H,如图:
则BG平行于平面 A1D1EF ,则点B到面 A1D1EF 的距离即为点G到面 A1D1EF 的距离,
易证 GH⊥ 平面 A1D1EF ,即GH即为点G到面 A1D1EF 的距离
∵△A1HG?△A1AF
∴HGAA1=GA1A1F
∴HG6=410
∴HG=2.4
∴HGAA1=GA1AF
VB?A1D1EF=s?=13×10×10×2.4=80
15.【答案】 解:由题意得以 AB 所在直线为轴将此三角形旋转一周,得两个圆锥,底面半径为 3×45=125 ,
母线长分别为 3,4, 因此所得旋转体的表面积为 π125×3+π125×4=84π5
8.3简单几何体的表面积与体积
1.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,底面菱形的对角线的长分别是 214 和 102 ,则这个棱柱的侧面积是(???? )???????
A.?130??????????????????????????????????????B.?140??????????????????????????????????????C.?150??????????????????????????????????????D.?160
2.在三楼锥 P?ABC 中, D 为 BC 的中点, PA⊥ 底面 ABC , AB⊥AC , AB=4 , AC=2 ,若 PD 与底面 ABC 所成角为45°,则三棱锥 P?ABC 的体积为(??? )
A.?5?????????????????????????????????????B.?453?????????????????????????????????????C.?45?????????????????????????????????????D.?554
3.运用祖暅原理计算球的体积时,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆 x24+y29=1 绕 y 轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于(??? ).
A.?8π??????????????????????????????????????B.?16π??????????????????????????????????????C.?24π??????????????????????????????????????D.?32π
4.现有一批大小不同的球体原材料,某工厂要加工出一个四棱锥零件,要求零件底面 ABCD 为正方形, AB=2 ,侧面 △PAD 为等边三角形,线段 BC 的中点为 E ,若 PE=1 ,则所需球体原材料的最小体积为(??? )
A.?82π3???????????????????????????????????B.?28π3 C.?9π???????????????????????????????????D.?143π3
5.已知正方体 ABCD?A1B1C1D1 的棱长为a , 点 E,F,G 分别为棱 AB,AA1,C1D1 的中点,下列结论中正确的个数是( ??)
①过 E,F,G 三点作正方体的截面,所得截面为正六边形;② B1D1// 平面 EFG ;③异面直线 EF 与 BD1 所成角的正切值为 2 ;④四面体 ACB1D1 的体积等于等 a33 .
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
6.在直三棱柱 ABC?A1B1C1 中, AB=BC=2 , ∠ABC=π2 ,若该直三棱柱的外接球表面积为 16π ,则此直三棱柱的高为(? ??).
A.?4????????????????????????????????????????B.?3????????????????????????????????????????C.?42????????????????????????????????????????D.?22
7.已知四棱锥 P?ABCD 中,底面 ABCD 是矩形,侧面 PAD 是正三角形,且侧面 PAD⊥ 底面 ABCD , AB=2 ,若四棱锥 P?ABCD 外接球的体积为 82π3 ,则该四棱锥的表面积为(??? )
A.?43????????????????????????????????????B.?63????????????????????????????????????C.?83????????????????????????????????????D.?103
8.如图,一个四棱柱形容器中盛有水,在底面 ABCD 中, AB//CD , AB=3 , CD=1 ,侧棱 AA1=4 ,若侧面 AA1B1B 水平放置时,水面恰好过 AD,BC,B1C1,A1D1 的中点,那么当底面 ABCD 水平放置时,水面高为(??? )
A.?2???????????????????????????????????????????B.?52???????????????????????????????????????????C.?3???????????????????????????????????????????D.?72
9.已知长方体 ABCD?A1B1C1D1 的底面是边长为2的正方形,高为4,E是 DD1 的中点,则三棱锥 B1?C1EC 的外接球的表面积为(??? )
A.?12π?????????????????????????????????????B.?20π?????????????????????????????????????C.?24π?????????????????????????????????????D.?32π
10.某中学开展劳动实习,学习加工制作食品包装盒.现有一张边长为6的正六边形硬纸片,如图所示,裁掉阴影部分,然后按虚线处折成高为 3 的正六棱柱无盖包装盒,则此包装盒的体积为( ??)
A.?144????????????????????????????????????????B.?72????????????????????????????????????????C.?36????????????????????????????????????????D.?24
11.已知三棱锥 P?ABC 的四个顶点在球 M 的球面上, PA=PB=PC , △ABC 是边长为2的正三角形, E , F 分别是 PA , AB 的中点, ∠CEF=90° ,则三棱锥 P?ABC 的体积为________,球 M 的表面积为________.
12.某圆台下底半径为2,上底半径为1,母线长为2,则该圆台的表面积为________.
13.2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意,沿着外墙面由低到高盘旋而成的“冰丝带”,就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹,冰上划痕成丝带,22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型,这种造型富有动感,体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体,其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就,如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式,但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理:“幂势既同,则积不容异”,才利用牟合方盖的体积推导出球的体积公式原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
(Ⅰ)利用祖暅原理推导半径为 R 的球的体积公式时,可以构造如图②所示的几何体 M ,几何体 M 的底面半径和高都为 R ,其底面和半球体的底面同在平面 α 内.设与平面 α 平行且距离为 d 的平面 β 截两个几何体得到两个截面,请在图②中用阴影画出与图①中阴影截面面积相等的图形并给出证明;
(Ⅱ)现将椭圆 x2a2+y2b2=1(a>b>0) 所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球 A , B (如图),类比(Ⅰ)中的方法,探究椭球 A 的体积公式,并写出椭球 A , B 的体积之比.
14.长方体 ABCD?A1B1C1D1 中, AB =12, BC =10, AA1 =6,过 A1D1 作长方体的截面 A1D1EF 使它成为正方形,
(1)求截面 A1D1EF 将正方体分成的两部分的体积比;
(2)求 VB?A1D1EF
15.已知 ΔABC 的三边分别是 AC=3,BC=4,AB=5 ,以 AB 所在直线为轴将此三角形旋转一周,求所得旋转体的表面积
1.【答案】 D 2.【答案】 B 3.【答案】 B 4.【答案】 A 5.【答案】 B 6.【答案】 D 7.【答案】 B 8.【答案】 B 9.【答案】 B 10.【答案】 B
11.【答案】 23;6π 12.【答案】 11π
13.【答案】 解:(Ⅰ)由图可知,图①几何体的为半径为 R 的半球,图②几何体为底面半径和高都为 R 的圆柱中挖掉了一个圆锥,与图①截面面积相等的图形是圆环(如阴影部分)
证明如下:
在图①中,设截面圆的圆心为 O1 ,易得截面圆 O1 的面积为 π(R2?d2) ,
在图②中,截面截圆锥得到的小圆的半径为 d ,所以,圆环的面积为 π(R2?d2) ,所以,截得的截面的面积相等
(Ⅱ)类比(Ⅰ)可知,椭圆的长半轴为 a ,短半轴为 b ,构造一个底面半径为 b ,高为 a 的圆柱,把半椭球与圆柱放在同一个平面上(如图),在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,即挖去的圆锥底面半径为 b ,高为 a ;
在半椭球截面圆的面积 πb2a2(a2?d2) ,
在圆柱内圆环的面积为 πb2?πb2a2d2=πb2a2(a2?d2)
∴距离平面 α 为 d 的平面截取两个几何体的平面面积相等,
根据祖暅原理得出椭球 A 的体积为:
VA=2(V圆柱?V圆锥)=2(π?b2?a?13π?b2?a)=4π3ab2 ,
同理:椭球 B 的体积为 VB=4π3a2b
所以,两个椭球 A , B 的体积之比为 ba .
14.【答案】 (1)解: ∵ A1D1EF 是正方形, AB =12, BC =10, AA1 =6
∴ A1F=10 , AF=8 , BF=4
∵ 截面 A1D1EF 将正方体分成的两部分为三棱柱和四棱柱,且高 ? 相等均为长方体侧棱长
∴ VA1AF?D1DF=sA1AF? , VA1FBB1?D1ECC1=sA1FBB1?
∴VA1AF?D1DFVA1FBB1?D1ECC1=sA1AFsA1FBB1=12×8×6(12+4)×62=12
(2)解:过点B作直线BG平行于 A1F 交 A1B1 于点G,过G作 A1F 的垂线交 A1F 于H,如图:
则BG平行于平面 A1D1EF ,则点B到面 A1D1EF 的距离即为点G到面 A1D1EF 的距离,
易证 GH⊥ 平面 A1D1EF ,即GH即为点G到面 A1D1EF 的距离
∵△A1HG?△A1AF
∴HGAA1=GA1A1F
∴HG6=410
∴HG=2.4
∴HGAA1=GA1AF
VB?A1D1EF=s?=13×10×10×2.4=80
15.【答案】 解:由题意得以 AB 所在直线为轴将此三角形旋转一周,得两个圆锥,底面半径为 3×45=125 ,
母线长分别为 3,4, 因此所得旋转体的表面积为 π125×3+π125×4=84π5
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
