8.5空间直线、平面的平行-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案)
文档属性
| 名称 | 8.5空间直线、平面的平行-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 23:46:21 | ||
图片预览


文档简介
1285875-3028958.5空间直线、平面的平行
8.5空间直线、平面的平行
1.已知 α,β,γ 是三个不同的平面,a , b是两条不同的直线,下列命题中正确的是(??? )
A.?若 α⊥γ,β⊥γ ,则 α//βB.?若 a⊥α,b⊥α ,则 a//b
C.?若 a//α,b//α ,则 a//b
D.?若 a//α,a//β ,则 α//β
2.如图,在正方体 ABCD?A1B1C1D1 中, E 为棱 CC1 的中点, F 为底面 ABCD 内一点,则“ F 为棱 BC 的中点”是“ EF// 平面 ABC1D1 ”的(??? )
A.?充分不必要条件?????????????B.?必要不充分条件?????????????C.?充要条件?????????????D.?既不充分也不必要条件
3.已知 α , β 表示不同平面,则 α//β 的充分条件是(??? )
A.?存在直线 a , b ,且 a,b?α , a//β , b//β
B.?存在直线 a , b ,且 a?α , b?β , a//β , b//α
C.?存在平面 γ , α⊥γ , β⊥γ
D.?存在直线 a,a⊥α , a⊥β
4.设 α,β,γ 为三个不同的平面,若 α⊥β ,则“ γ//β 是“ α⊥γ ”的(??? )
A.?充分不必要条件?????????????B.?充要条件?????????????C.?必要不充分条件?????????????D.?既不充分也不必要条件
5.在空间中,下列命题是真命题的是(??? )
A.?经过三个点有且只有一个平面
B.?平行于同一平面的两直线相互平行
C.?如果两个角的两条边分别对应平行,那么这两个角相等
D.?如果两个相交平面垂直于同一个平面,那么它们的交线也垂直于这个平面
6.已知下列四个命题,其中真命题的个数为(??? )
①空间三条互相平行的直线 a , b , c ,都与直线 d 相交,则 a , b , c 三条直线共面;②若直线 m⊥ 平面 α ,直线 n// 平面 α ,则 m⊥n ;③平面 α∩ 平面 β= 直线 m ,直线 a// 平面 α ,直线 a// 平面 β ,则 a//m ;④垂直于同一个平面的两个平面互相平行.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
7.在空间直角坐标系中,已知 A(1,2,3) , , C(3,2,1) , D(4,3,0) ,则直线 AB 与 CD 的位置关系是(???? )
A.?垂直????????????????????????????????B.?平行????????????????????????????????C.?异面????????????????????????????????D.?相交但不垂直
8.如果直线l的方向向量是 a=(?2,0,1) ,且直线l上有一点P不在平面 α 内,平面 α 的法向量是 b=(2,0,4) ,那么(??? ).
A.?直线l与平面 α 垂直
B.?直线l与平面 α 平行
C.?直线l在平面 α 内
D.?直线l与平面 α 相交但不垂直
9.α 、 β 为不重合的平面, a 、 b 为两条直线,下列命题正确的为(??? )
A.?若 a?α , b?β , α//β ,则 a//b
B.?若 a//b , b?β ,则 a//β
C.?若 α⊥β , a?α ,则 a⊥β
D.?若 a⊥α , b⊥β , a⊥b ,则 α⊥β
10.若直线 l 与平面 α 不平行,且直线 l 也不在平面 α 内,则 (??? )
A.?α 内不存在与 l 异面的直线?????????????????????????????????B.?α 内存在与 l 平行的直线
C.?α 内存在唯一的直线与 l 相交?????????????????????????????D.?α 内存在无数条与 l 垂直的直线
11.给出下列命题:
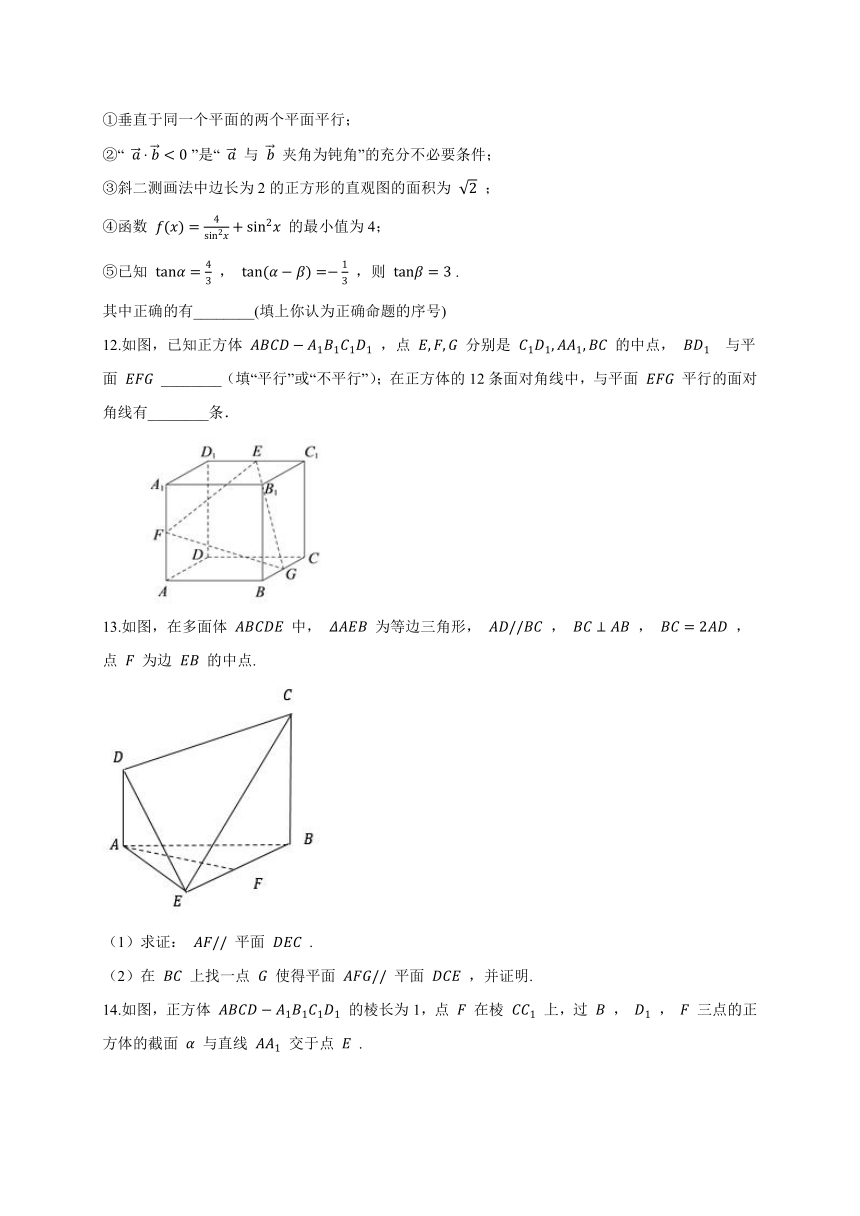
①垂直于同一个平面的两个平面平行;
②“ a?b<0 ”是“ a 与 b 夹角为钝角”的充分不必要条件;
③斜二测画法中边长为2的正方形的直观图的面积为 2 ;
④函数 f(x)=4sin2x+sin2x 的最小值为4;
⑤已知 tanα=43 , tan(α?β)=?13 ,则 tanβ=3 .
其中正确的有________(填上你认为正确命题的序号)
12.如图,已知正方体 ABCD?A1B1C1D1 ,点 E,F,G 分别是 C1D1,AA1,BC 的中点, BD1 与平面 EFG ________(填“平行”或“不平行”);在正方体的12条面对角线中,与平面 EFG 平行的面对角线有________条.
13.如图,在多面体 ABCDE 中, ΔAEB 为等边三角形, AD//BC , BC⊥AB , BC=2AD ,点 F 为边 EB 的中点.
(1)求证: AF// 平面 DEC .
(2)在 BC 上找一点 G 使得平面 AFG// 平面 DCE ,并证明.
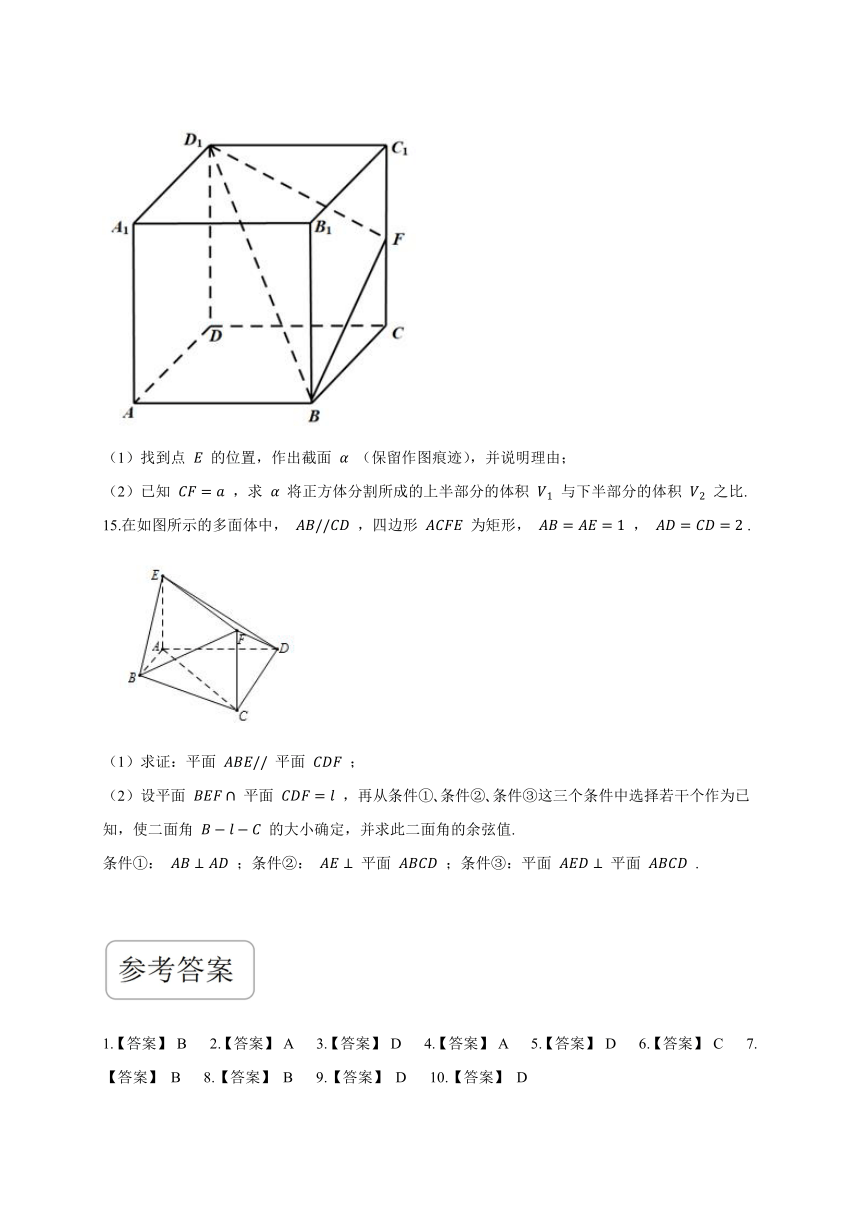
14.如图,正方体 ABCD?A1B1C1D1 的棱长为1,点 F 在棱 CC1 上,过 B , D1 , F 三点的正方体的截面 α 与直线 AA1 交于点 E .
(1)找到点 E 的位置,作出截面 α (保留作图痕迹),并说明理由;
(2)已知 CF=a ,求 α 将正方体分割所成的上半部分的体积 V1 与下半部分的体积 V2 之比.
15.在如图所示的多面体中, AB//CD ,四边形 ACFE 为矩形, AB=AE=1 , AD=CD=2 .
(1)求证:平面 ABE// 平面 CDF ;
(2)设平面 BEF∩ 平面 CDF=l ,再从条件①?条件②?条件③这三个条件中选择若干个作为已知,使二面角 B?l?C 的大小确定,并求此二面角的余弦值.
条件①: AB⊥AD ;条件②: AE⊥ 平面 ABCD ;条件③:平面 AED⊥ 平面 ABCD .
1.【答案】 B 2.【答案】 A 3.【答案】 D 4.【答案】 A 5.【答案】 D 6.【答案】 C 7.【答案】 B 8.【答案】 B 9.【答案】 D 10.【答案】 D
11.【答案】 ③⑤ 12.【答案】 不平行;6
13.【答案】 (1)取 EC 中点 M ,连接 FM , DM ,
∵ AD//BC//FM , AD=12BC=MF ,
∴ ADMF 是平行四边形,∴ AF//DM ,
∵ AF? 平面 DEC , DM? 平面 DEC ,∴ AF// 平面 DEC .
(2)点 G 为 BC 的中点.
证:连接 FG , AG ,
因为 G 、 F 分别是 BC , BE 的中点,所以 GF//CE ,
又 GF? 平面 DCE , CE? 平面 DCE ,所以 GF// 平面 DCE ,
又因为 AD//BC , AD=12BC ,所以 AD//GC 且 AD=GC ,
即四边形 ADCG 是平行四边形,所以 DC//AG ,
因为 AG? 平面 DCE ,所以 AG// 平面 DCE .
又因为 AG∩GF=G ,所以平面 AFG// 平面 DCE .
14.【答案】 (1)解:在正方形 CDD1C1 中,过 F 作 FG//DC ,且交棱 DD1 于点 G ,
连接 AG ,在正方形 ADD1A1 内过 D1 作 D1E//AG ,且交棱 AA1 于点 E ,
连接 EB , ED1 ,则四边形 BED1F 就是要作的截面 α .
理由:由题意,平面 α∩ 平面 AD1=D1E ,
α∩ 平面 BC1=BF ,平面 AD1// 平面 BC1 ,
应有 D1E//BF ,
同理, BE//FD1 ,所以四边形 BED1F 应是平行四边形,
由作图过程, FG//DC , FG=DC ,又 AB//DC , AB=DC ,
所以 AB//FG , AB=FG ,所以四边形 ABFG 是平行四边形,
所以 AG//BF , AG=BF ,
由作图过程, D1E//AG .又 EA//D1G ,
所以四边形 EAGD1 是平行四边形,所以 D1E//AG , D1E=AG ,
又 AG//BF , AG=BF ,所以 D1E//BF ,且 D1E=BF ,
所以 BED1F 是平行四边形,四边形 BED1F 就是要作的截面
(2)解:由题意, CF=a(0由(1)的证明过程,可得 A1E=a ,
连接 D1B1 ,则平面 α 将正方体分割所成的上半部分的几何体可视为四棱锥 D1?A1EBB1 与四棱锥 D1?B1BFC1 的组合体,
V1=VD1?A1EBB1+VD1?B1BFC1 =13×(a+1)×12×1+13×[(1?a)+1]×12×1 =12 ,
而该正方体的体积 V=1 , V2=V?V1=1?12=12 .所以 V1:V2=1
15.【答案】 (1)证明:因为四边形 ACFE 为矩形,所以 AE//CF ,
又 AE? 平面 CDF ; CF? 平面 CDF ;
所以 AE// 平面 CDF ;
又 AB//CD , AB? 平面 CDF ; CD? 平面 CDF ;
所以 AB// 平面 CDF ;
又 AB∩AE=A ,
所以平面 ABE// 平面 CDF ;
(2)解:选条件①: AB⊥AD ;条件②: AE⊥ 平面 ABCD ;
以A为原点,以AB,AD,AE分别为x,y,z轴建立如图所示空间直角坐标系;
则 A(0,0,0),B(1,0,0),E(1,0,0),F(2,2,1),D(0,2,0),C(2,2,0) ,
所以 EB=(1,0?1),EF=(2,2?1) ,
设平面CDF的一个法向量为 n=(x,y,z) ,即 n=(0,1,0) ,
设平面EBF的一个法向量为 m=(x,y,z) ,
则 {EB?m=0EF?m=0 ,即 {x?z=02x+2y=0 ,
令 x=1 ,则 y=?1,z=1 ,则 m=(1,?1,1) ,
设二面角 B?l?C 为 θ ,
所以 cosθ=n?m|n|?|m|=?13=?33
选条件①: AB⊥AD ;条件③:平面 AED⊥ 平面 ABCD .
因为 AB⊥AD ,平面 AED⊥ 平面 ABCD .
所以 AB⊥ 平面 AED
因为 AB//CD ,
所以 CD⊥ 平面 AED ,
所以 CD⊥DE
因为 CD=2,EC=AE2+AC2=3 ,
所以 ED=EC2?CD2=5 ,即 AE2+AD2=ED2 ,
所以 AE⊥AD ,
因为平面 AED⊥ 平面 ABCD .
所以 AE⊥ 平面 ABCD ,
以A为原点,以AB,AD,AE分别为x,y,z轴建立如图所示空间直角坐标系;
则 A(0,0,0),B(1,0,0),E(1,0,0),F(2,2,1),D(0,2,0),C(2,2,0) ,
所以 EB=(1,0?1),EF=(2,2?1) ,
设平面CDF的一个法向量为 n=(x,y,z) ,即 n=(0,1,0) ,
设平面EBF的一个法向量为 m=(x,y,z) ,
则 {EB?m=0EF?m=0 ,即 {x?z=02x+2y=0 ,
令 x=1 ,则 y=?1,z=1 ,则 m=(1,?1,1) ,
设二面角 B?l?C 为 θ ,
所以 cosθ=n?m|n|?|m|=?13=?33
8.5空间直线、平面的平行
1.已知 α,β,γ 是三个不同的平面,a , b是两条不同的直线,下列命题中正确的是(??? )
A.?若 α⊥γ,β⊥γ ,则 α//βB.?若 a⊥α,b⊥α ,则 a//b
C.?若 a//α,b//α ,则 a//b
D.?若 a//α,a//β ,则 α//β
2.如图,在正方体 ABCD?A1B1C1D1 中, E 为棱 CC1 的中点, F 为底面 ABCD 内一点,则“ F 为棱 BC 的中点”是“ EF// 平面 ABC1D1 ”的(??? )
A.?充分不必要条件?????????????B.?必要不充分条件?????????????C.?充要条件?????????????D.?既不充分也不必要条件
3.已知 α , β 表示不同平面,则 α//β 的充分条件是(??? )
A.?存在直线 a , b ,且 a,b?α , a//β , b//β
B.?存在直线 a , b ,且 a?α , b?β , a//β , b//α
C.?存在平面 γ , α⊥γ , β⊥γ
D.?存在直线 a,a⊥α , a⊥β
4.设 α,β,γ 为三个不同的平面,若 α⊥β ,则“ γ//β 是“ α⊥γ ”的(??? )
A.?充分不必要条件?????????????B.?充要条件?????????????C.?必要不充分条件?????????????D.?既不充分也不必要条件
5.在空间中,下列命题是真命题的是(??? )
A.?经过三个点有且只有一个平面
B.?平行于同一平面的两直线相互平行
C.?如果两个角的两条边分别对应平行,那么这两个角相等
D.?如果两个相交平面垂直于同一个平面,那么它们的交线也垂直于这个平面
6.已知下列四个命题,其中真命题的个数为(??? )
①空间三条互相平行的直线 a , b , c ,都与直线 d 相交,则 a , b , c 三条直线共面;②若直线 m⊥ 平面 α ,直线 n// 平面 α ,则 m⊥n ;③平面 α∩ 平面 β= 直线 m ,直线 a// 平面 α ,直线 a// 平面 β ,则 a//m ;④垂直于同一个平面的两个平面互相平行.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
7.在空间直角坐标系中,已知 A(1,2,3) , , C(3,2,1) , D(4,3,0) ,则直线 AB 与 CD 的位置关系是(???? )
A.?垂直????????????????????????????????B.?平行????????????????????????????????C.?异面????????????????????????????????D.?相交但不垂直
8.如果直线l的方向向量是 a=(?2,0,1) ,且直线l上有一点P不在平面 α 内,平面 α 的法向量是 b=(2,0,4) ,那么(??? ).
A.?直线l与平面 α 垂直
B.?直线l与平面 α 平行
C.?直线l在平面 α 内
D.?直线l与平面 α 相交但不垂直
9.α 、 β 为不重合的平面, a 、 b 为两条直线,下列命题正确的为(??? )
A.?若 a?α , b?β , α//β ,则 a//b
B.?若 a//b , b?β ,则 a//β
C.?若 α⊥β , a?α ,则 a⊥β
D.?若 a⊥α , b⊥β , a⊥b ,则 α⊥β
10.若直线 l 与平面 α 不平行,且直线 l 也不在平面 α 内,则 (??? )
A.?α 内不存在与 l 异面的直线?????????????????????????????????B.?α 内存在与 l 平行的直线
C.?α 内存在唯一的直线与 l 相交?????????????????????????????D.?α 内存在无数条与 l 垂直的直线
11.给出下列命题:
①垂直于同一个平面的两个平面平行;
②“ a?b<0 ”是“ a 与 b 夹角为钝角”的充分不必要条件;
③斜二测画法中边长为2的正方形的直观图的面积为 2 ;
④函数 f(x)=4sin2x+sin2x 的最小值为4;
⑤已知 tanα=43 , tan(α?β)=?13 ,则 tanβ=3 .
其中正确的有________(填上你认为正确命题的序号)
12.如图,已知正方体 ABCD?A1B1C1D1 ,点 E,F,G 分别是 C1D1,AA1,BC 的中点, BD1 与平面 EFG ________(填“平行”或“不平行”);在正方体的12条面对角线中,与平面 EFG 平行的面对角线有________条.
13.如图,在多面体 ABCDE 中, ΔAEB 为等边三角形, AD//BC , BC⊥AB , BC=2AD ,点 F 为边 EB 的中点.
(1)求证: AF// 平面 DEC .
(2)在 BC 上找一点 G 使得平面 AFG// 平面 DCE ,并证明.
14.如图,正方体 ABCD?A1B1C1D1 的棱长为1,点 F 在棱 CC1 上,过 B , D1 , F 三点的正方体的截面 α 与直线 AA1 交于点 E .
(1)找到点 E 的位置,作出截面 α (保留作图痕迹),并说明理由;
(2)已知 CF=a ,求 α 将正方体分割所成的上半部分的体积 V1 与下半部分的体积 V2 之比.
15.在如图所示的多面体中, AB//CD ,四边形 ACFE 为矩形, AB=AE=1 , AD=CD=2 .
(1)求证:平面 ABE// 平面 CDF ;
(2)设平面 BEF∩ 平面 CDF=l ,再从条件①?条件②?条件③这三个条件中选择若干个作为已知,使二面角 B?l?C 的大小确定,并求此二面角的余弦值.
条件①: AB⊥AD ;条件②: AE⊥ 平面 ABCD ;条件③:平面 AED⊥ 平面 ABCD .
1.【答案】 B 2.【答案】 A 3.【答案】 D 4.【答案】 A 5.【答案】 D 6.【答案】 C 7.【答案】 B 8.【答案】 B 9.【答案】 D 10.【答案】 D
11.【答案】 ③⑤ 12.【答案】 不平行;6
13.【答案】 (1)取 EC 中点 M ,连接 FM , DM ,
∵ AD//BC//FM , AD=12BC=MF ,
∴ ADMF 是平行四边形,∴ AF//DM ,
∵ AF? 平面 DEC , DM? 平面 DEC ,∴ AF// 平面 DEC .
(2)点 G 为 BC 的中点.
证:连接 FG , AG ,
因为 G 、 F 分别是 BC , BE 的中点,所以 GF//CE ,
又 GF? 平面 DCE , CE? 平面 DCE ,所以 GF// 平面 DCE ,
又因为 AD//BC , AD=12BC ,所以 AD//GC 且 AD=GC ,
即四边形 ADCG 是平行四边形,所以 DC//AG ,
因为 AG? 平面 DCE ,所以 AG// 平面 DCE .
又因为 AG∩GF=G ,所以平面 AFG// 平面 DCE .
14.【答案】 (1)解:在正方形 CDD1C1 中,过 F 作 FG//DC ,且交棱 DD1 于点 G ,
连接 AG ,在正方形 ADD1A1 内过 D1 作 D1E//AG ,且交棱 AA1 于点 E ,
连接 EB , ED1 ,则四边形 BED1F 就是要作的截面 α .
理由:由题意,平面 α∩ 平面 AD1=D1E ,
α∩ 平面 BC1=BF ,平面 AD1// 平面 BC1 ,
应有 D1E//BF ,
同理, BE//FD1 ,所以四边形 BED1F 应是平行四边形,
由作图过程, FG//DC , FG=DC ,又 AB//DC , AB=DC ,
所以 AB//FG , AB=FG ,所以四边形 ABFG 是平行四边形,
所以 AG//BF , AG=BF ,
由作图过程, D1E//AG .又 EA//D1G ,
所以四边形 EAGD1 是平行四边形,所以 D1E//AG , D1E=AG ,
又 AG//BF , AG=BF ,所以 D1E//BF ,且 D1E=BF ,
所以 BED1F 是平行四边形,四边形 BED1F 就是要作的截面
(2)解:由题意, CF=a(0
连接 D1B1 ,则平面 α 将正方体分割所成的上半部分的几何体可视为四棱锥 D1?A1EBB1 与四棱锥 D1?B1BFC1 的组合体,
V1=VD1?A1EBB1+VD1?B1BFC1 =13×(a+1)×12×1+13×[(1?a)+1]×12×1 =12 ,
而该正方体的体积 V=1 , V2=V?V1=1?12=12 .所以 V1:V2=1
15.【答案】 (1)证明:因为四边形 ACFE 为矩形,所以 AE//CF ,
又 AE? 平面 CDF ; CF? 平面 CDF ;
所以 AE// 平面 CDF ;
又 AB//CD , AB? 平面 CDF ; CD? 平面 CDF ;
所以 AB// 平面 CDF ;
又 AB∩AE=A ,
所以平面 ABE// 平面 CDF ;
(2)解:选条件①: AB⊥AD ;条件②: AE⊥ 平面 ABCD ;
以A为原点,以AB,AD,AE分别为x,y,z轴建立如图所示空间直角坐标系;
则 A(0,0,0),B(1,0,0),E(1,0,0),F(2,2,1),D(0,2,0),C(2,2,0) ,
所以 EB=(1,0?1),EF=(2,2?1) ,
设平面CDF的一个法向量为 n=(x,y,z) ,即 n=(0,1,0) ,
设平面EBF的一个法向量为 m=(x,y,z) ,
则 {EB?m=0EF?m=0 ,即 {x?z=02x+2y=0 ,
令 x=1 ,则 y=?1,z=1 ,则 m=(1,?1,1) ,
设二面角 B?l?C 为 θ ,
所以 cosθ=n?m|n|?|m|=?13=?33
选条件①: AB⊥AD ;条件③:平面 AED⊥ 平面 ABCD .
因为 AB⊥AD ,平面 AED⊥ 平面 ABCD .
所以 AB⊥ 平面 AED
因为 AB//CD ,
所以 CD⊥ 平面 AED ,
所以 CD⊥DE
因为 CD=2,EC=AE2+AC2=3 ,
所以 ED=EC2?CD2=5 ,即 AE2+AD2=ED2 ,
所以 AE⊥AD ,
因为平面 AED⊥ 平面 ABCD .
所以 AE⊥ 平面 ABCD ,
以A为原点,以AB,AD,AE分别为x,y,z轴建立如图所示空间直角坐标系;
则 A(0,0,0),B(1,0,0),E(1,0,0),F(2,2,1),D(0,2,0),C(2,2,0) ,
所以 EB=(1,0?1),EF=(2,2?1) ,
设平面CDF的一个法向量为 n=(x,y,z) ,即 n=(0,1,0) ,
设平面EBF的一个法向量为 m=(x,y,z) ,
则 {EB?m=0EF?m=0 ,即 {x?z=02x+2y=0 ,
令 x=1 ,则 y=?1,z=1 ,则 m=(1,?1,1) ,
设二面角 B?l?C 为 θ ,
所以 cosθ=n?m|n|?|m|=?13=?33
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
