9.1随机抽样-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案)
文档属性
| 名称 | 9.1随机抽样-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 122.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 00:00:00 | ||
图片预览



文档简介
1285875-3028959.1 随机抽样
9.1 随机抽样
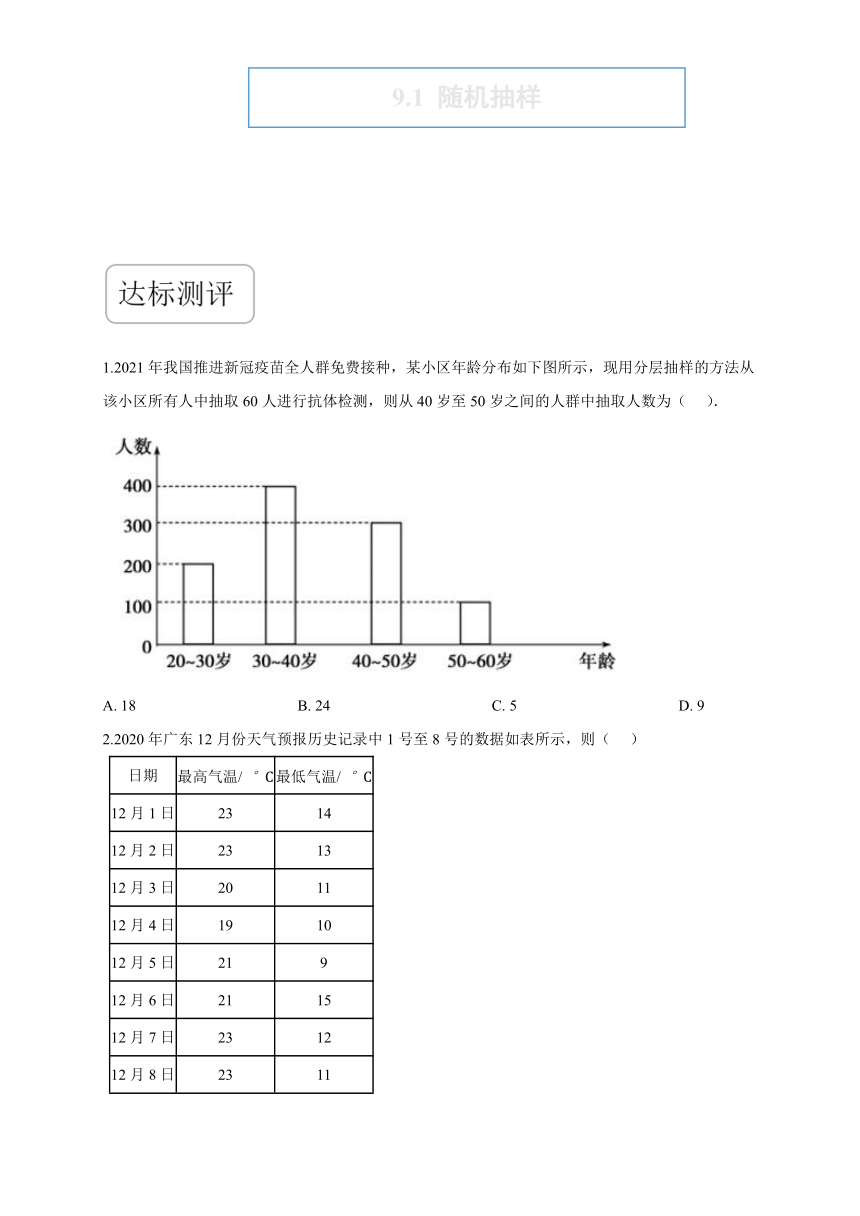
1.2021年我国推进新冠疫苗全人群免费接种,某小区年龄分布如下图所示,现用分层抽样的方法从该小区所有人中抽取60人进行抗体检测,则从40岁至50岁之间的人群中抽取人数为(??? ).
A.?18??????????????????????????????????????????B.?24??????????????????????????????????????????C.?5??????????????????????????????????????????D.?9
2.2020年广东12月份天气预报历史记录中1号至8号的数据如表所示,则(??? )
日期
最高气温/ °C
最低气温/ °C
12月1日
23
14
12月2日
23
13
12月3日
20
11
12月4日
19
10
12月5日
21
9
12月6日
21
15
12月7日
23
12
12月8日
23
11
A.?这8天的最高气温的极差为 5°C
B.?这8天的最高气温的中位数为 23°C
C.?这8天的最低气温的极差为 5°C
D.?这8天的最低气温的中位数为 11.5°C
3.构建德智体美劳全面培养的教育体系是我国教育一直以来努力的方向.某中学积极响应党的号召,开展各项有益于德智体美劳全面发展的活动.如图所示的是该校高三(1)、(2)班两个班级在某次活动中的德智体美劳的评价得分对照图(得分越高,说明该项教育越好).下列说法正确的是(??? )
A.?高三(2)班五项评价得分的极差为1.5
B.?除体育外,高三(1)班的各项评价得分均高于高三(2)班对应的得分
C.?高三(1)班五项评价得分的平均数比高三(2)班五项评价得分的平均数要高
D.?各项评价得分中,这两班的体育得分相差最大
4.某中学高一?高二和高三各年级人数见下表.采用分层抽样的方法调查学生的健康状况,在抽取的样本中,高二年级有20人,那么该样本中高三年级的人数为(??? )
年级
人数
高一
550
高二
500
高三
450
合计
1500
A.?18?????????????????????????????????????????B.?22?????????????????????????????????????????C.?40?????????????????????????????????????????D.?60
5.某企业有职工150人,其中高级职称有15人,中级职称有45人,一般职员有90人,现抽取30人,进行分层抽样,则各职称人数分别为(??? )
A.?5,10,15?????????????????????????B.?3,9,18?????????????????????????C.?3,10,17?????????????????????????D.?5,9,16
6.现有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为(?? )
A.?5,10,15,20,25
B.?5,15,20,35,40
C.?5,11,17,23,29
D.?10,20,30,40,50
7.数据12,12,12,14,15的平均数与众数的差为(??? )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.?-1??????????????????????????????????????????D.?-2
8.某校要调查该校1200名学生的身体健康情况,中男生700名,女生500名,现按性别用分层抽样的方法从中抽取120名学生的体检报告,下列说法错误的是(?? )
A.?总体容量是1200?????????????B.?样本容量是120
C.?男生应抽取70名?????????????D.?女生应抽取40名
9.一位高三学生在半年时间里经历了七次大考,他把这七次考试的历史成绩统计为如图所示的茎叶图,则该学生成绩的平均数和中位数分别为(??? )
7983454793
A.?84,83???????????????????????????????B.?84,84???????????????????????????????C.?85,84???????????????????????????????D.?85,85
10.某服装生产厂家研发了甲、乙、丙三种新式时装准备投入市场销售.甲时装共加工了1900件,乙时装共加工了1400件,丙时装共加工了900件.在投入市场前,厂家采用分层抽样的方式从三种新式时装中选取210件在小范围内试销售,则应从乙时装中选取开始(??? )
A.?90件????????????????????????????????????B.?70件????????????????????????????????????C.?60件????????????????????????????????????D.?50件
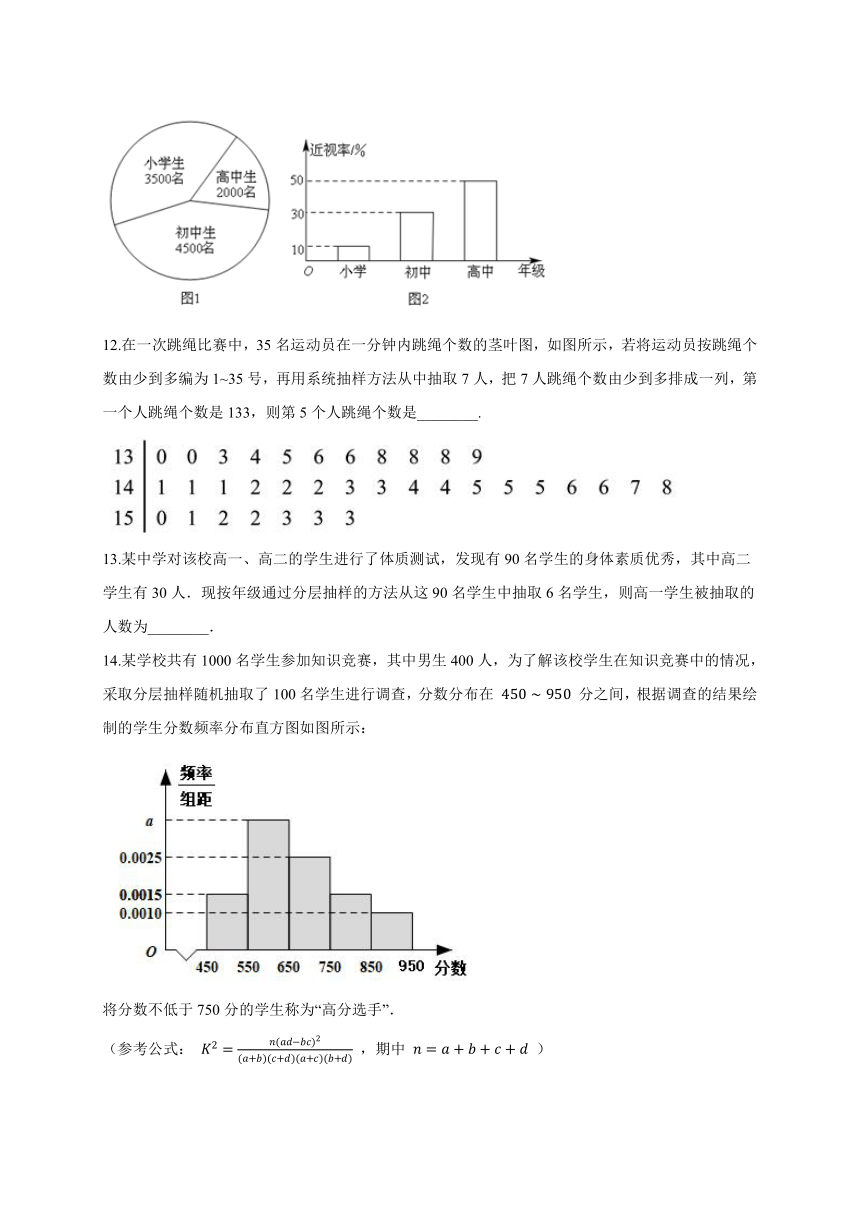
11.已知某地区中小学生的人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则抽取的高中生中近视的人数为________.
12.在一次跳绳比赛中,35名运动员在一分钟内跳绳个数的茎叶图,如图所示,若将运动员按跳绳个数由少到多编为1~35号,再用系统抽样方法从中抽取7人,把7人跳绳个数由少到多排成一列,第一个人跳绳个数是133,则第5个人跳绳个数是________.
13.某中学对该校高一、高二的学生进行了体质测试,发现有90名学生的身体素质优秀,其中高二学生有30人.现按年级通过分层抽样的方法从这90名学生中抽取6名学生,则高一学生被抽取的人数为________.
14.某学校共有1000名学生参加知识竞赛,其中男生400人,为了解该校学生在知识竞赛中的情况,采取分层抽样随机抽取了100名学生进行调查,分数分布在 450?950 分之间,根据调查的结果绘制的学生分数频率分布直方图如图所示:
将分数不低于750分的学生称为“高分选手”.
(参考公式: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ,期中 n=a+b+c+d )
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)求 a 的值,并估计该校学生分数的平均数、中位数和众数(同一组中的数据用该组区间的中点值作代表);
(2)现采用分层抽样的方式从分数落在 [550,650) , [750,850) 内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高分选手”的学生人数为随机变量 X ,求 X 的分布列及数学期望;
(3)若样本中属于“高分选手”的女生有10人,完成下列 2×2 列联表,并判断是否有97.5%%的把握认为该校学生属于“高分选手”与“性别”有关?
?
属于“高分选手”
不属于“高分选手”
合计
男生
?
?
?
女生
?
?
?
合计
?
?
?
15.“工资条里显红利,个税新政人民心”,随着2021年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革至2019年实施以来发挥巨大作用.个税新政主要内容包括:
⑴个税起征点为5000元;
⑵每月应纳税所得额(含税) = 收入-个税起征点-专项附加扣除;
⑶专项附加扣除包括住房?子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如表:
旧个税税率表(税起征点3500元)
新个税税率表(个税起征点5000元)
缴税级数
每月应纳税所得额(含税) = 收入-个税起征点
税率(%)
每月应纳税所得额(含税)=收入-个税起征点 ? 专项附加扣除
税率(%)
1
不超过1500元部分
3
不超过3000元部分
3
2
超过1500元至4500元部分
10
超过3000元至12000元部分
10
3
超过4500元至9000元的部分
20
超过12000元至25000元的部分
20
4
超过9000元至35000元的部分
25
超过25000元至35000元的部分
25
5
超过35000元至55000元部分
30
超过35000元至55000元部分
30
?
?
?
?
?
随机抽取某市1000名同一收入层级的IT从业者的相关资料,经统计分析,预估他们2021年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是 2:1:1:1 ;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的IT从业者都独自享受专项附加扣除,将预估的该市该收入层级的IT从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)求该市该收入层级的IT从业者2021年月缴个税的所有可能及其概率.
(2)根据新旧个税方案,估计从2021年1月开始,经过多少个月,该市该收入层级的 IT 从业者各月少缴交的个税之和就超过2019年的月收入?
16.学校为了制定培养学生阅读习惯,指导学生提高阅读能力的方案,需了解全校学生的阅读情况,现随机调查了200名学生每周阅读时间 X (单位:小时)并绘制如图所示的频率分布直方图.
(1)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为 [6.5,7.5) , [7.5,8.5) 的学生中抽取6名参加座谈会,你认为6个名额应该怎么分配?
(2)利用样本估计总体的方法,估计全校每周阅读时间的中位数 a ( a 的值精确到0.01).
1.【答案】 A 2.【答案】 D 3.【答案】 C 4.【答案】 A 5.【答案】 B 6.【答案】 D 7.【答案】 B 8.【答案】 D 9.【答案】 C 10.【答案】 B
11.【答案】 20 12.【答案】 145 13.【答案】 4
14.【答案】 (1)解:由题意知 100×(0.0015+a+0.0025+0.0015+0.001)=1 ,
解得 a=0.0035 ,
样本平均数为 x=500×0.15+600×0.35+700×0.25+800×0.15+900×0.10=670 ,
中位数650,众数600
(2)解:由题意,从 [550,650) 中抽取7人,从 [750,850) 中抽取3人,
随机变量 x 的所有可能取值有0,1,2,3.
P(x=k)=C3kC73?kC103(k=0,1,2,3) ,
所以随机变量 X 的分布列为:
P
0
1
2
3
X
35120
63120
21120
1120
随机变量 X 的数学期望 E(X)=63120+2×21120+3×1120=910
(3)解:由题可知,样本中男生40人,女姓60人,属于“高分选手”的25人,其中女姓10人;得出以下 2×2 列联表;
?
属于“高分选手”
不属于“高分选手”
合计
男生
15
25
40
女生
10
50
60
合计
25
75
100
K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)=100(10×25?15×50)225×75×40×60=509>5.024 ,
所以有97.5%%的把握认为该校学生属于“高分选手”与性别有关
15.【答案】 (1)解:由题意,既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是 2:1:1:1 .
①既不符合子女教育扣除又不符合赡养老人扣除的人群每月应纳税所得额为
24000?5000?1000=18000 元,
月缴个税为 3000×0.03+9000×0.1+6000×0.2=2190 元,其概率为 25 ;
②只符合子女教育扣除但不符合赡养老人扣除的人群每月应纳税所得额为
24000?5000?1000?1000=17000 元,
月缴个税为 3000×0.03+9000×0.1+5000×0.2=1990 元,其概率为 15 ;
③只符合赡养老人扣除但不符合子女教育扣除的人群每月应纳税所得额为 24000?5000?1000?2000=16000 元,
月缴个税为 3000×0.03+9000×0.1+4000×0.2=1790 元,其概率为 15 ;
④既符合子女教育扣除又符合赡养老人扣除的人群每月应纳税所得额为 24000?5000?1000?1000?2000=15000 元,
月缴个税为 3000×0.03+9000×0.1+3000×0.2=1590 元,其概率为 15 ;
(2)解:在旧政策下,该收入阶层的 IT 从业者每月应纳税所得额为 24000?3500=20500 元,
故月缴个税为 1500×0.03+3000×0.1+4500×0.2+11500×0.25=4120 元,
在新政策下,该收入阶层的 IT 从业者每月应纳税所得额为 2190×25+(1990+1790+1590)×15=1950 元,
每月少缴个税 4120?1950=2170 元,
设经过 x 个月该市该收入阶层的 IT 从业者各月少缴交的个税之和就超过2019年的月收入,
则 2170x≥24000 ,又 x∈N ,解得 x≥12(x∈N) ,
所以经过12个月,该市该收入阶层的 IT 从业者各月少缴交的个税之和就超过2019年的月收入.
16.【答案】 (1)解:每周阅读时间为 [6.5,7.5) 的学生中抽取2名,
每周阅读时间为 [7.5,8.5) 的学生中抽取4名.
理由:每周阅读时间为 [6.5,7.5) 与每周阅读时间为 [7.5,8.5) 是差异明显的两层,
为保持样本结构与总体结构的一致性,提高样本的代表性,
宜采用分层抽样的方法抽取样本,
∵两者频率分别为0.1,0.2,∴按照1:2进行名额分配.
(2)解:∵ 0.03+0.1+0.2+0.35=0.68>0.5 ,
∴中位数 a∈[8.5,9.5) ,
由 0.03+0.1+0.2+(a?8.5)×0.35=0.5 ,
解得 a=0.5?0.330.35+8.5≈8.99 .
9.1 随机抽样
1.2021年我国推进新冠疫苗全人群免费接种,某小区年龄分布如下图所示,现用分层抽样的方法从该小区所有人中抽取60人进行抗体检测,则从40岁至50岁之间的人群中抽取人数为(??? ).
A.?18??????????????????????????????????????????B.?24??????????????????????????????????????????C.?5??????????????????????????????????????????D.?9
2.2020年广东12月份天气预报历史记录中1号至8号的数据如表所示,则(??? )
日期
最高气温/ °C
最低气温/ °C
12月1日
23
14
12月2日
23
13
12月3日
20
11
12月4日
19
10
12月5日
21
9
12月6日
21
15
12月7日
23
12
12月8日
23
11
A.?这8天的最高气温的极差为 5°C
B.?这8天的最高气温的中位数为 23°C
C.?这8天的最低气温的极差为 5°C
D.?这8天的最低气温的中位数为 11.5°C
3.构建德智体美劳全面培养的教育体系是我国教育一直以来努力的方向.某中学积极响应党的号召,开展各项有益于德智体美劳全面发展的活动.如图所示的是该校高三(1)、(2)班两个班级在某次活动中的德智体美劳的评价得分对照图(得分越高,说明该项教育越好).下列说法正确的是(??? )
A.?高三(2)班五项评价得分的极差为1.5
B.?除体育外,高三(1)班的各项评价得分均高于高三(2)班对应的得分
C.?高三(1)班五项评价得分的平均数比高三(2)班五项评价得分的平均数要高
D.?各项评价得分中,这两班的体育得分相差最大
4.某中学高一?高二和高三各年级人数见下表.采用分层抽样的方法调查学生的健康状况,在抽取的样本中,高二年级有20人,那么该样本中高三年级的人数为(??? )
年级
人数
高一
550
高二
500
高三
450
合计
1500
A.?18?????????????????????????????????????????B.?22?????????????????????????????????????????C.?40?????????????????????????????????????????D.?60
5.某企业有职工150人,其中高级职称有15人,中级职称有45人,一般职员有90人,现抽取30人,进行分层抽样,则各职称人数分别为(??? )
A.?5,10,15?????????????????????????B.?3,9,18?????????????????????????C.?3,10,17?????????????????????????D.?5,9,16
6.现有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为(?? )
A.?5,10,15,20,25
B.?5,15,20,35,40
C.?5,11,17,23,29
D.?10,20,30,40,50
7.数据12,12,12,14,15的平均数与众数的差为(??? )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.?-1??????????????????????????????????????????D.?-2
8.某校要调查该校1200名学生的身体健康情况,中男生700名,女生500名,现按性别用分层抽样的方法从中抽取120名学生的体检报告,下列说法错误的是(?? )
A.?总体容量是1200?????????????B.?样本容量是120
C.?男生应抽取70名?????????????D.?女生应抽取40名
9.一位高三学生在半年时间里经历了七次大考,他把这七次考试的历史成绩统计为如图所示的茎叶图,则该学生成绩的平均数和中位数分别为(??? )
7983454793
A.?84,83???????????????????????????????B.?84,84???????????????????????????????C.?85,84???????????????????????????????D.?85,85
10.某服装生产厂家研发了甲、乙、丙三种新式时装准备投入市场销售.甲时装共加工了1900件,乙时装共加工了1400件,丙时装共加工了900件.在投入市场前,厂家采用分层抽样的方式从三种新式时装中选取210件在小范围内试销售,则应从乙时装中选取开始(??? )
A.?90件????????????????????????????????????B.?70件????????????????????????????????????C.?60件????????????????????????????????????D.?50件
11.已知某地区中小学生的人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则抽取的高中生中近视的人数为________.
12.在一次跳绳比赛中,35名运动员在一分钟内跳绳个数的茎叶图,如图所示,若将运动员按跳绳个数由少到多编为1~35号,再用系统抽样方法从中抽取7人,把7人跳绳个数由少到多排成一列,第一个人跳绳个数是133,则第5个人跳绳个数是________.
13.某中学对该校高一、高二的学生进行了体质测试,发现有90名学生的身体素质优秀,其中高二学生有30人.现按年级通过分层抽样的方法从这90名学生中抽取6名学生,则高一学生被抽取的人数为________.
14.某学校共有1000名学生参加知识竞赛,其中男生400人,为了解该校学生在知识竞赛中的情况,采取分层抽样随机抽取了100名学生进行调查,分数分布在 450?950 分之间,根据调查的结果绘制的学生分数频率分布直方图如图所示:
将分数不低于750分的学生称为“高分选手”.
(参考公式: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ,期中 n=a+b+c+d )
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)求 a 的值,并估计该校学生分数的平均数、中位数和众数(同一组中的数据用该组区间的中点值作代表);
(2)现采用分层抽样的方式从分数落在 [550,650) , [750,850) 内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高分选手”的学生人数为随机变量 X ,求 X 的分布列及数学期望;
(3)若样本中属于“高分选手”的女生有10人,完成下列 2×2 列联表,并判断是否有97.5%%的把握认为该校学生属于“高分选手”与“性别”有关?
?
属于“高分选手”
不属于“高分选手”
合计
男生
?
?
?
女生
?
?
?
合计
?
?
?
15.“工资条里显红利,个税新政人民心”,随着2021年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革至2019年实施以来发挥巨大作用.个税新政主要内容包括:
⑴个税起征点为5000元;
⑵每月应纳税所得额(含税) = 收入-个税起征点-专项附加扣除;
⑶专项附加扣除包括住房?子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如表:
旧个税税率表(税起征点3500元)
新个税税率表(个税起征点5000元)
缴税级数
每月应纳税所得额(含税) = 收入-个税起征点
税率(%)
每月应纳税所得额(含税)=收入-个税起征点 ? 专项附加扣除
税率(%)
1
不超过1500元部分
3
不超过3000元部分
3
2
超过1500元至4500元部分
10
超过3000元至12000元部分
10
3
超过4500元至9000元的部分
20
超过12000元至25000元的部分
20
4
超过9000元至35000元的部分
25
超过25000元至35000元的部分
25
5
超过35000元至55000元部分
30
超过35000元至55000元部分
30
?
?
?
?
?
随机抽取某市1000名同一收入层级的IT从业者的相关资料,经统计分析,预估他们2021年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是 2:1:1:1 ;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的IT从业者都独自享受专项附加扣除,将预估的该市该收入层级的IT从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)求该市该收入层级的IT从业者2021年月缴个税的所有可能及其概率.
(2)根据新旧个税方案,估计从2021年1月开始,经过多少个月,该市该收入层级的 IT 从业者各月少缴交的个税之和就超过2019年的月收入?
16.学校为了制定培养学生阅读习惯,指导学生提高阅读能力的方案,需了解全校学生的阅读情况,现随机调查了200名学生每周阅读时间 X (单位:小时)并绘制如图所示的频率分布直方图.
(1)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为 [6.5,7.5) , [7.5,8.5) 的学生中抽取6名参加座谈会,你认为6个名额应该怎么分配?
(2)利用样本估计总体的方法,估计全校每周阅读时间的中位数 a ( a 的值精确到0.01).
1.【答案】 A 2.【答案】 D 3.【答案】 C 4.【答案】 A 5.【答案】 B 6.【答案】 D 7.【答案】 B 8.【答案】 D 9.【答案】 C 10.【答案】 B
11.【答案】 20 12.【答案】 145 13.【答案】 4
14.【答案】 (1)解:由题意知 100×(0.0015+a+0.0025+0.0015+0.001)=1 ,
解得 a=0.0035 ,
样本平均数为 x=500×0.15+600×0.35+700×0.25+800×0.15+900×0.10=670 ,
中位数650,众数600
(2)解:由题意,从 [550,650) 中抽取7人,从 [750,850) 中抽取3人,
随机变量 x 的所有可能取值有0,1,2,3.
P(x=k)=C3kC73?kC103(k=0,1,2,3) ,
所以随机变量 X 的分布列为:
P
0
1
2
3
X
35120
63120
21120
1120
随机变量 X 的数学期望 E(X)=63120+2×21120+3×1120=910
(3)解:由题可知,样本中男生40人,女姓60人,属于“高分选手”的25人,其中女姓10人;得出以下 2×2 列联表;
?
属于“高分选手”
不属于“高分选手”
合计
男生
15
25
40
女生
10
50
60
合计
25
75
100
K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)=100(10×25?15×50)225×75×40×60=509>5.024 ,
所以有97.5%%的把握认为该校学生属于“高分选手”与性别有关
15.【答案】 (1)解:由题意,既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是 2:1:1:1 .
①既不符合子女教育扣除又不符合赡养老人扣除的人群每月应纳税所得额为
24000?5000?1000=18000 元,
月缴个税为 3000×0.03+9000×0.1+6000×0.2=2190 元,其概率为 25 ;
②只符合子女教育扣除但不符合赡养老人扣除的人群每月应纳税所得额为
24000?5000?1000?1000=17000 元,
月缴个税为 3000×0.03+9000×0.1+5000×0.2=1990 元,其概率为 15 ;
③只符合赡养老人扣除但不符合子女教育扣除的人群每月应纳税所得额为 24000?5000?1000?2000=16000 元,
月缴个税为 3000×0.03+9000×0.1+4000×0.2=1790 元,其概率为 15 ;
④既符合子女教育扣除又符合赡养老人扣除的人群每月应纳税所得额为 24000?5000?1000?1000?2000=15000 元,
月缴个税为 3000×0.03+9000×0.1+3000×0.2=1590 元,其概率为 15 ;
(2)解:在旧政策下,该收入阶层的 IT 从业者每月应纳税所得额为 24000?3500=20500 元,
故月缴个税为 1500×0.03+3000×0.1+4500×0.2+11500×0.25=4120 元,
在新政策下,该收入阶层的 IT 从业者每月应纳税所得额为 2190×25+(1990+1790+1590)×15=1950 元,
每月少缴个税 4120?1950=2170 元,
设经过 x 个月该市该收入阶层的 IT 从业者各月少缴交的个税之和就超过2019年的月收入,
则 2170x≥24000 ,又 x∈N ,解得 x≥12(x∈N) ,
所以经过12个月,该市该收入阶层的 IT 从业者各月少缴交的个税之和就超过2019年的月收入.
16.【答案】 (1)解:每周阅读时间为 [6.5,7.5) 的学生中抽取2名,
每周阅读时间为 [7.5,8.5) 的学生中抽取4名.
理由:每周阅读时间为 [6.5,7.5) 与每周阅读时间为 [7.5,8.5) 是差异明显的两层,
为保持样本结构与总体结构的一致性,提高样本的代表性,
宜采用分层抽样的方法抽取样本,
∵两者频率分别为0.1,0.2,∴按照1:2进行名额分配.
(2)解:∵ 0.03+0.1+0.2+0.35=0.68>0.5 ,
∴中位数 a∈[8.5,9.5) ,
由 0.03+0.1+0.2+(a?8.5)×0.35=0.5 ,
解得 a=0.5?0.330.35+8.5≈8.99 .
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
