9.2用样本估计总体-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案)
文档属性
| 名称 | 9.2用样本估计总体-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 198.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 00:00:00 | ||
图片预览


文档简介
1285875-3028959.2 用样本估计总体
9.2 用样本估计总体
1.某高中高一、高二、高三年级的人数分别为1200、900、900人.现按照分层抽样的方法抽取300名学生,调查学生每周平均参加体育运动的时间.样本数据(单位:小时)整理后得到如图所示的频率分布直方图.下列说法错误的是(?? )
A.?每个年级抽取的人数分别为120、90、90人
B.?估计高一年级每周平均体育运动时间不足4小时的人数约为300人
C.?估计该校学生每周平均体育运动时间不少于8小时的人数约为600人
D.?估计该校学生每周平均体育运动时间不少于8小时的百分比为10%
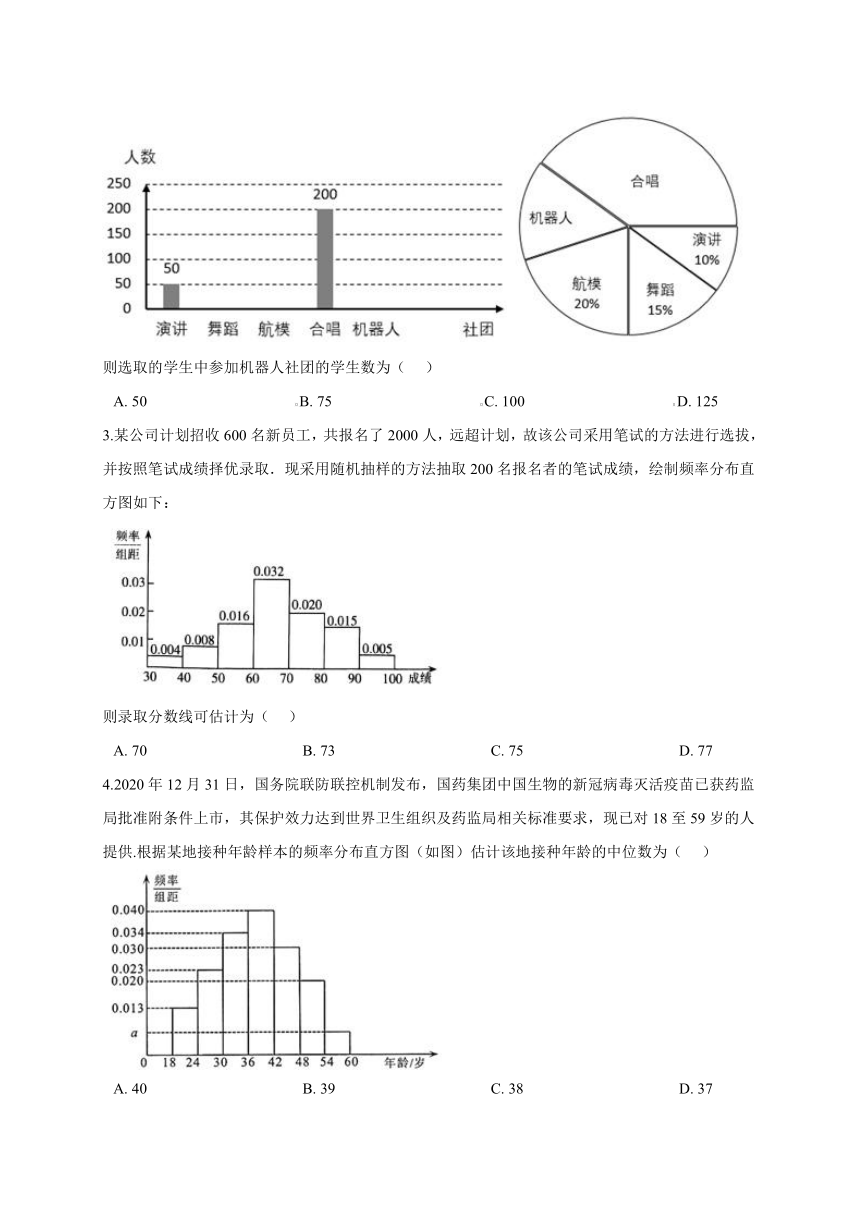
2.某学校组建了演讲,舞蹈?航模?合唱,机器人五个社团,全校 3000 名学生每人都参加且只参加其中一个社团,校团委从这 3000 名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为(??? )
A.?50???????????????????????????????????????B.?75???????????????????????????????????????C.?100???????????????????????????????????????D.?125
3.某公司计划招收600名新员工,共报名了2000人,远超计划,故该公司采用笔试的方法进行选拔,并按照笔试成绩择优录取.现采用随机抽样的方法抽取200名报名者的笔试成绩,绘制频率分布直方图如下:
则录取分数线可估计为(??? )
A.?70?????????????????????????????????????????B.?73?????????????????????????????????????????C.?75?????????????????????????????????????????D.?77
4.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如图)估计该地接种年龄的中位数为(??? )
A.?40?????????????????????????????????????????B.?39?????????????????????????????????????????C.?38?????????????????????????????????????????D.?37
5.甲、乙两名射击运动爱好者在相同条件下各射击10次,中靶环数情况如图所示.则甲、乙两人中靶环数的方差分别为(?? )
A.?7,7???????????????????????????????B.?7,1.2???????????????????????????????C.?1.1,2.3???????????????????????????????D.?1.2,5.4
6.某校抽取100名学生做体能测认,其中百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成五组:第一组 [13,14) ,第二组 [14,15) , ? ,第五组 [17,18] .如图是按上述分组方法得到的频率分布直方图,若成绩低于 a 即为优秀,如果优秀的人数为14人,则 a 的估计值是( ??)
A.?14???????????????????????????????????????B.?14.5???????????????????????????????????????C.?15???????????????????????????????????????D.?15.5
7.某校对高三年级800名学生的数学成绩进行统计分析.全年级同学的成绩全部介于80分与150分之间,将他们的成绩按照 [80,90) , [90,100) , [100,110) , [110,120) , [120,130) , [130,140) , [140,150] 分组,整理得到如下频率分布直方图,则成绩在 [120,130) 内的学生人数为(??? )
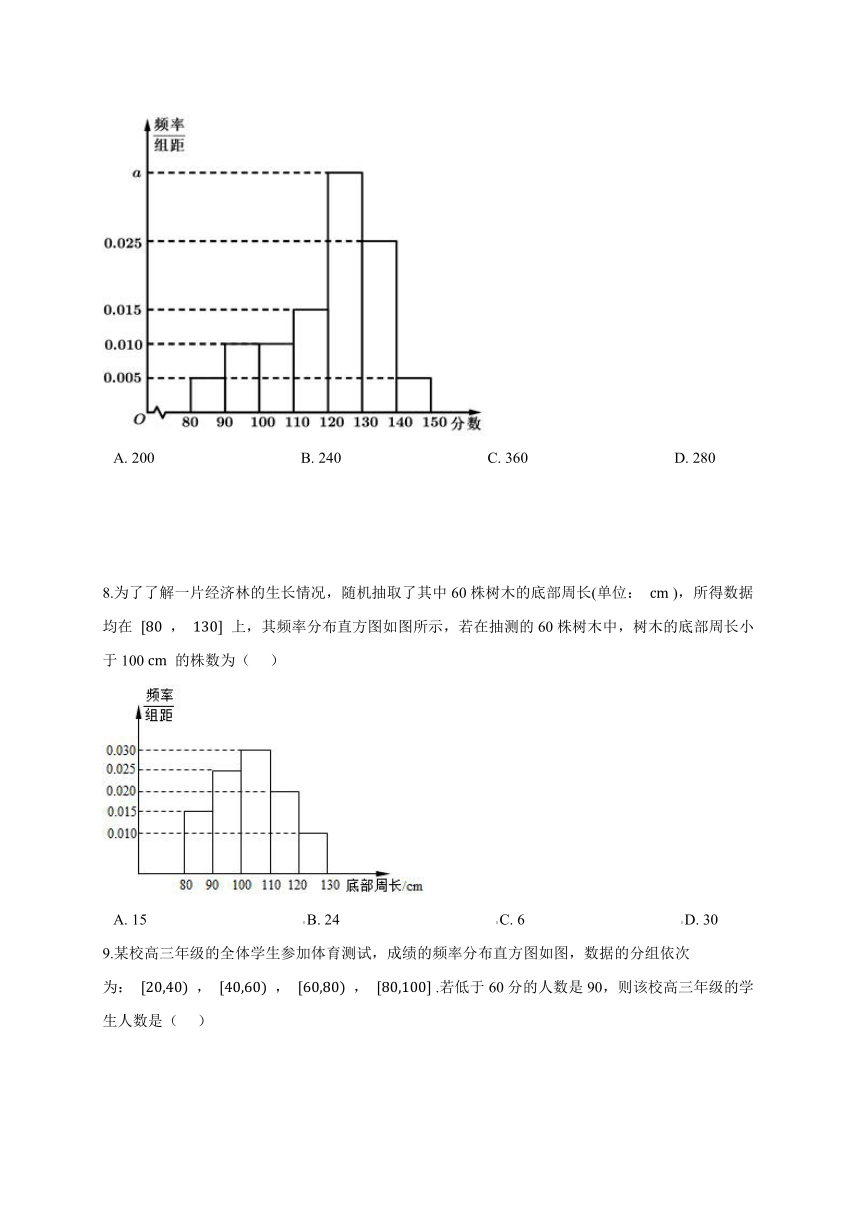
A.?200??????????????????????????????????????B.?240??????????????????????????????????????C.?360??????????????????????????????????????D.?280
8.为了了解一片经济林的生长情况,随机抽取了其中60株树木的底部周长(单位: cm ),所得数据均在 [80 , 130] 上,其频率分布直方图如图所示,若在抽测的60株树木中,树木的底部周长小于100 cm 的株数为(??? )
A.?15?????????????????????????????????????????B.?24?????????????????????????????????????????C.?6?????????????????????????????????????????D.?30
9.某校高三年级的全体学生参加体育测试,成绩的频率分布直方图如图,数据的分组依次为: [20,40) , [40,60) , [60,80) , [80,100] .若低于60分的人数是90,则该校高三年级的学生人数是(??? )
A.?270??????????????????????????????????????B.?300??????????????????????????????????????C.?330??????????????????????????????????????D.?360
10.天津市某中学组织高二年级学生参加普法知识考试(满分100分),考试成绩的频率分布直方图如图,数据(成绩)的分组依次为 [20,40) , [40,60) , [60,80) , [80,100] ,若成绩低于60分的人数是180,则考试成绩在区间 [60,80) 内的人数是(??? )
A.?180??????????????????????????????????????B.?240??????????????????????????????????????C.?280??????????????????????????????????????D.?320
11.某班40名学生,在一次考试中统计所得平均分为80分,方差为70,后来发现有两名同学的成绩有损,甲实得80分错记为60分,乙实得70分错记为90分,则更正后的方差为________.
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是________.
①平均数 x≤3 ;??? ②标准差 S≤2 ;??? ③平均数 x≤3 且标准差 S≤2 ;
④平均数 x≤3 且极差小于或等于2;????? ⑤众数等于1且极差小于或等于4.
13.2020年10月,中共中央办公厅、国务院办公厅印发了《关于全面加强和改进新时代学校体育工作的意见》,某地积极开展中小学健康促进行动,发挥以体育智、以体育心功能,决定在2021年体育中考中再增加一定的分数,规定:考生须参加立定跳远、掷实心球、一分钟跳绳三项测试,其中一分钟跳绳满分20分.学校为掌握九年级学生一分钟跳绳情况,随机抽取了100名学生测试,其成绩均在 [165,215] 间,并得到如图所示频率分布直方图,计分规则如下表:
一分钟跳绳个数
[165,175)
[175,185)
[185,195)
[195,205)
[205,215]
得分
16
17
18
19
20
(1)补全频率分布直方图,并根据频率分布直方图估计样本中位数;
(2)若两人可组成一个小队,并且两人得分之和小于35分,则称该小队为“潜力队”,用频率估计概率,求从进行测试的100名学生中任意选取2人,恰好选到“潜力队”的概率.
14.某教练统计了甲、乙两名三级跳远运动员连续5次的跳远成绩(单位:米),统计数据如图所示.
(1)分别求甲、乙跳远成绩的平均数;
(2)通过平均数和方差分析甲、乙两名运动员的平均水平和发挥的稳定性.
15.自从新冠肺炎疫情暴发以来,各地都采取积极有效的防控措施,使疫情得到了有效的控制.某地对100名年龄在 [20,45] 岁,患病后已经康复的居民做了数据统计,绘成如图所示不完整的频率分布直方图.统计员在绘制频率分布直方图的过程中所搜集的数据只能确定年龄在 [30,35) 与 [40,45] 的新冠肺炎康复人数之和是年龄在 [35,40) 的新冠肺炎康复人数的3倍,且 [30,35) 组的频率比 [40,45] 组的频率多0.15.
(1)分别求 [30,35) , [35,40) , [40,45] 组对应的频率;
(2)求年龄在 [35,45] 的新冠肺炎康复人数.
1.【答案】 D 2.【答案】 B 3.【答案】 C 4.【答案】 C 5.【答案】 D 6.【答案】 B 7.【答案】 B 8.【答案】 B 9.【答案】 B 10.【答案】 B
11.【答案】 60 12.【答案】 (4)(5)
13.【答案】 (1)解:如图,在 [195,205) 的频率为 1?10×(0.005+0.006+0.009+0.050)=0.3 ,
则频率/组距 =0.030 ;
[165,175) 的频率为: 0.005×10=0.05 ;
[175,185) 的频率为: 0.009×10=0.09 ;
[185,195) 的频率为: 0.050×10=0.5 ,
则样本中位数一定落在 [185,195) ,
则中位数为 185+0.5?0.05?0.090.050=192.2
(2)解:根据频率分布直方图,一分钟跳绳个数在 [165,175) 则可得16分,
人数为: 100×0.005×10=5 (人);
一分钟跳绳个数在 [175,185) 则可得17分,人数为: 100×0.009×10=9 (人);
一分钟跳绳个数在 [185,195) 则可得18分,人数为: 100×0.050×10=50 (人).
则“潜力队”的两人构成有4种情况,分别得分之和为 32 , 33 , 34 , 34 .
则恰好选到“潜力队”的概率 P=C52C1002+C51C91C1002 +C92C1002+C51C501C1002=3414950
14.【答案】 (1)解:根据题意可知 x甲=15(8+9+12+12+14)=11 ,
x乙=15(7+9+11+13+15)=11
(2)解: s甲2=15[(8?11)2+(9?11)2+(12?11)2 +(12?11)2+(14?11)2]=4.8 ,
s乙2=15[(7?11)2+(9?11)2+(11?11)2 +(13?11)2+(15?11)2]=8 .
∵x甲=x乙 , s甲2∴ 甲、乙两名运动员的平均水平相当,甲的发挥更稳定
15.【答案】 (1)解:由频率分布直方图,得 [20,25) 组对应的频率为 0.01×5=0.05 , [25,30) 组对应的频率为 0.07×5=0.35 .
设 [30,35) , [35,40) , [40,45] 组对应的频率分别为 x , y , z ,则
{x+y+z=1?0.05?0.35x+z=3yx?z=0.15 ,解得 {x=0.3y=0.15z=0.15
(2)解:因为 [35,45] 对应的频率为 0.15+0.15=0.3 ,
所以年龄在 [35,45] 的新冠肺炎康复人数为 100×0.3=30
9.2 用样本估计总体
1.某高中高一、高二、高三年级的人数分别为1200、900、900人.现按照分层抽样的方法抽取300名学生,调查学生每周平均参加体育运动的时间.样本数据(单位:小时)整理后得到如图所示的频率分布直方图.下列说法错误的是(?? )
A.?每个年级抽取的人数分别为120、90、90人
B.?估计高一年级每周平均体育运动时间不足4小时的人数约为300人
C.?估计该校学生每周平均体育运动时间不少于8小时的人数约为600人
D.?估计该校学生每周平均体育运动时间不少于8小时的百分比为10%
2.某学校组建了演讲,舞蹈?航模?合唱,机器人五个社团,全校 3000 名学生每人都参加且只参加其中一个社团,校团委从这 3000 名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为(??? )
A.?50???????????????????????????????????????B.?75???????????????????????????????????????C.?100???????????????????????????????????????D.?125
3.某公司计划招收600名新员工,共报名了2000人,远超计划,故该公司采用笔试的方法进行选拔,并按照笔试成绩择优录取.现采用随机抽样的方法抽取200名报名者的笔试成绩,绘制频率分布直方图如下:
则录取分数线可估计为(??? )
A.?70?????????????????????????????????????????B.?73?????????????????????????????????????????C.?75?????????????????????????????????????????D.?77
4.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如图)估计该地接种年龄的中位数为(??? )
A.?40?????????????????????????????????????????B.?39?????????????????????????????????????????C.?38?????????????????????????????????????????D.?37
5.甲、乙两名射击运动爱好者在相同条件下各射击10次,中靶环数情况如图所示.则甲、乙两人中靶环数的方差分别为(?? )
A.?7,7???????????????????????????????B.?7,1.2???????????????????????????????C.?1.1,2.3???????????????????????????????D.?1.2,5.4
6.某校抽取100名学生做体能测认,其中百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成五组:第一组 [13,14) ,第二组 [14,15) , ? ,第五组 [17,18] .如图是按上述分组方法得到的频率分布直方图,若成绩低于 a 即为优秀,如果优秀的人数为14人,则 a 的估计值是( ??)
A.?14???????????????????????????????????????B.?14.5???????????????????????????????????????C.?15???????????????????????????????????????D.?15.5
7.某校对高三年级800名学生的数学成绩进行统计分析.全年级同学的成绩全部介于80分与150分之间,将他们的成绩按照 [80,90) , [90,100) , [100,110) , [110,120) , [120,130) , [130,140) , [140,150] 分组,整理得到如下频率分布直方图,则成绩在 [120,130) 内的学生人数为(??? )
A.?200??????????????????????????????????????B.?240??????????????????????????????????????C.?360??????????????????????????????????????D.?280
8.为了了解一片经济林的生长情况,随机抽取了其中60株树木的底部周长(单位: cm ),所得数据均在 [80 , 130] 上,其频率分布直方图如图所示,若在抽测的60株树木中,树木的底部周长小于100 cm 的株数为(??? )
A.?15?????????????????????????????????????????B.?24?????????????????????????????????????????C.?6?????????????????????????????????????????D.?30
9.某校高三年级的全体学生参加体育测试,成绩的频率分布直方图如图,数据的分组依次为: [20,40) , [40,60) , [60,80) , [80,100] .若低于60分的人数是90,则该校高三年级的学生人数是(??? )
A.?270??????????????????????????????????????B.?300??????????????????????????????????????C.?330??????????????????????????????????????D.?360
10.天津市某中学组织高二年级学生参加普法知识考试(满分100分),考试成绩的频率分布直方图如图,数据(成绩)的分组依次为 [20,40) , [40,60) , [60,80) , [80,100] ,若成绩低于60分的人数是180,则考试成绩在区间 [60,80) 内的人数是(??? )
A.?180??????????????????????????????????????B.?240??????????????????????????????????????C.?280??????????????????????????????????????D.?320
11.某班40名学生,在一次考试中统计所得平均分为80分,方差为70,后来发现有两名同学的成绩有损,甲实得80分错记为60分,乙实得70分错记为90分,则更正后的方差为________.
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是________.
①平均数 x≤3 ;??? ②标准差 S≤2 ;??? ③平均数 x≤3 且标准差 S≤2 ;
④平均数 x≤3 且极差小于或等于2;????? ⑤众数等于1且极差小于或等于4.
13.2020年10月,中共中央办公厅、国务院办公厅印发了《关于全面加强和改进新时代学校体育工作的意见》,某地积极开展中小学健康促进行动,发挥以体育智、以体育心功能,决定在2021年体育中考中再增加一定的分数,规定:考生须参加立定跳远、掷实心球、一分钟跳绳三项测试,其中一分钟跳绳满分20分.学校为掌握九年级学生一分钟跳绳情况,随机抽取了100名学生测试,其成绩均在 [165,215] 间,并得到如图所示频率分布直方图,计分规则如下表:
一分钟跳绳个数
[165,175)
[175,185)
[185,195)
[195,205)
[205,215]
得分
16
17
18
19
20
(1)补全频率分布直方图,并根据频率分布直方图估计样本中位数;
(2)若两人可组成一个小队,并且两人得分之和小于35分,则称该小队为“潜力队”,用频率估计概率,求从进行测试的100名学生中任意选取2人,恰好选到“潜力队”的概率.
14.某教练统计了甲、乙两名三级跳远运动员连续5次的跳远成绩(单位:米),统计数据如图所示.
(1)分别求甲、乙跳远成绩的平均数;
(2)通过平均数和方差分析甲、乙两名运动员的平均水平和发挥的稳定性.
15.自从新冠肺炎疫情暴发以来,各地都采取积极有效的防控措施,使疫情得到了有效的控制.某地对100名年龄在 [20,45] 岁,患病后已经康复的居民做了数据统计,绘成如图所示不完整的频率分布直方图.统计员在绘制频率分布直方图的过程中所搜集的数据只能确定年龄在 [30,35) 与 [40,45] 的新冠肺炎康复人数之和是年龄在 [35,40) 的新冠肺炎康复人数的3倍,且 [30,35) 组的频率比 [40,45] 组的频率多0.15.
(1)分别求 [30,35) , [35,40) , [40,45] 组对应的频率;
(2)求年龄在 [35,45] 的新冠肺炎康复人数.
1.【答案】 D 2.【答案】 B 3.【答案】 C 4.【答案】 C 5.【答案】 D 6.【答案】 B 7.【答案】 B 8.【答案】 B 9.【答案】 B 10.【答案】 B
11.【答案】 60 12.【答案】 (4)(5)
13.【答案】 (1)解:如图,在 [195,205) 的频率为 1?10×(0.005+0.006+0.009+0.050)=0.3 ,
则频率/组距 =0.030 ;
[165,175) 的频率为: 0.005×10=0.05 ;
[175,185) 的频率为: 0.009×10=0.09 ;
[185,195) 的频率为: 0.050×10=0.5 ,
则样本中位数一定落在 [185,195) ,
则中位数为 185+0.5?0.05?0.090.050=192.2
(2)解:根据频率分布直方图,一分钟跳绳个数在 [165,175) 则可得16分,
人数为: 100×0.005×10=5 (人);
一分钟跳绳个数在 [175,185) 则可得17分,人数为: 100×0.009×10=9 (人);
一分钟跳绳个数在 [185,195) 则可得18分,人数为: 100×0.050×10=50 (人).
则“潜力队”的两人构成有4种情况,分别得分之和为 32 , 33 , 34 , 34 .
则恰好选到“潜力队”的概率 P=C52C1002+C51C91C1002 +C92C1002+C51C501C1002=3414950
14.【答案】 (1)解:根据题意可知 x甲=15(8+9+12+12+14)=11 ,
x乙=15(7+9+11+13+15)=11
(2)解: s甲2=15[(8?11)2+(9?11)2+(12?11)2 +(12?11)2+(14?11)2]=4.8 ,
s乙2=15[(7?11)2+(9?11)2+(11?11)2 +(13?11)2+(15?11)2]=8 .
∵x甲=x乙 , s甲2
15.【答案】 (1)解:由频率分布直方图,得 [20,25) 组对应的频率为 0.01×5=0.05 , [25,30) 组对应的频率为 0.07×5=0.35 .
设 [30,35) , [35,40) , [40,45] 组对应的频率分别为 x , y , z ,则
{x+y+z=1?0.05?0.35x+z=3yx?z=0.15 ,解得 {x=0.3y=0.15z=0.15
(2)解:因为 [35,45] 对应的频率为 0.15+0.15=0.3 ,
所以年龄在 [35,45] 的新冠肺炎康复人数为 100×0.3=30
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
