10.3频率与概率-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案)
文档属性
| 名称 | 10.3频率与概率-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 126.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 00:00:00 | ||
图片预览


文档简介
1285875-30289510.3频率与概率
10.3频率与概率
1.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率;先由计算器给出0到9之间取整数值的随机数,指定0、1、2、3表示没有击中目标, 4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数,根据以下数据估计该射击运动员射击4次至少击中3次的概率为(?? )
7527? 0293? 7140? 9857? 0347? 4373? 8636? 6947? 1417? 4698
0371? 6233? 2616? 8045? 6011? 3661? 9597? 7424? 7610? 4281
A.?0.4??????????????????????????????????????B.?0.45??????????????????????????????????????C.?0.5??????????????????????????????????????D.?0.55
2.已知P是△ABC所在平面内﹣点, PB+PC+2PA=0 ,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是(?? )
A.?23??????????????????????????????????????????B.?12??????????????????????????????????????????C.?13??????????????????????????????????????????D.?14
3.从区间[0,1]内随机抽取2n个数 x1 , x2 ,… xn , y1 ,.. , yn 构成n个数对( x1 , y1 ),…,( xn , yn ),其中两数的平方和不小于1的数对共有m个,则用随机模拟的方法得到圆周率π的近似值为(?? )
A.?mn????????????????????????????????????B.?4mn????????????????????????????????????C.?n?mn????????????????????????????????????D.?4(n?m)n
4.为了了解奥运五环及其内部所占面积与单独五个圆环及其内部面积之和的比值P , 某同学设计了如右图所示的数学模型,通过随机模拟的方法,在长为8,宽为5的矩形内随机取了 N 个点,经统计落入五环及其内部的点的个数为 n ,若圆环的半径为1,则比值 P 的近似值为(?? )
A.?32n5πN???????????????????????????????????B.?32nπN???????????????????????????????????C.?8nπN???????????????????????????????????D.?5n32πN
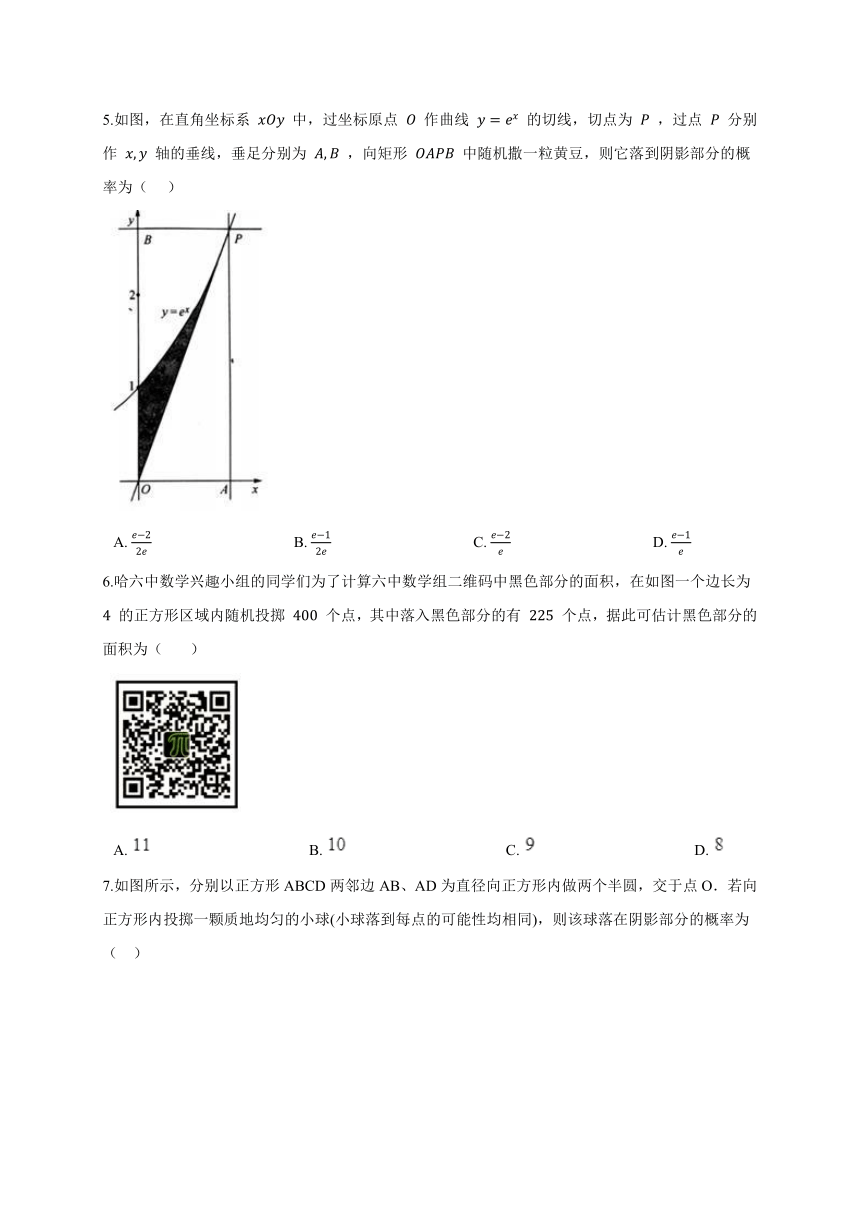
5.如图,在直角坐标系 xOy 中,过坐标原点 O 作曲线 y=ex 的切线,切点为 P ,过点 P 分别作 x,y 轴的垂线,垂足分别为 A,B ,向矩形 OAPB 中随机撒一粒黄豆,则它落到阴影部分的概率为(??? )
A.?e?22e?????????????????????????????????????B.?e?12e?????????????????????????????????????C.?e?2e?????????????????????????????????????D.?e?1e
6.哈六中数学兴趣小组的同学们为了计算六中数学组二维码中黑色部分的面积,在如图一个边长为 4 的正方形区域内随机投掷 400 个点,其中落入黑色部分的有 225 个点,据此可估计黑色部分的面积为(????? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.如图所示,分别以正方形ABCD两邻边AB、AD为直径向正方形内做两个半圆,交于点O.若向正方形内投掷一颗质地均匀的小球(小球落到每点的可能性均相同),则该球落在阴影部分的概率为( ??)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
8.分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域所示,若向该正方形内随机投一点,则该点落在阴影区域的概率为(?? )
A.?4?π2????????????????????????????????????B.?π?22????????????????????????????????????C.?4?π4????????????????????????????????????D.?π?24
9.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为5的正方形将其包含在内,并向该正方形内随机投掷1000个点,己知恰有400个点落在阴影部分,据此可估计阴影部分的面积是(?? )
A.?2??????????????????????????????????????????B.?3??????????????????????????????????????????C.?10??????????????????????????????????????????D.?15
10.下列关于用转盘进行随机模拟的说法中正确的是( ??)
A.?旋转的次数的多少不会影响估计的结果???????????????B.?旋转的次数越多,估计的结果越精确
C.?旋转时可以按规律旋转???????????????????????????????????????D.?转盘的半径越大,估计的结果越精确
11.如图,在平放的边长为1的正方形中随机撒1000粒豆子,有380粒落到红心阴影部分上,据此估计红心阴影部分的面积为________.
12.如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为400颗,以此实验数据为依据可以估计出该不规则图形的面积为________平方米.(用分数作答)
13.用随机模拟方法求函数 y=x ?与x轴和直线x=1围成的图形的面积.
14.一份测试题包括6道选择题,每题只有一个选项是正确的.如果一个学生对每一道题都随机猜一个答案,用随机模拟方法估计该学生至少答对3道题的概率.
15.如图,面积为 S 的正方形 ABCD 中有一个不规则的图形 M ,可按下面方法估计 M 的面积:在正方形 ABCD 中随机投掷 n 个点,若 n 个点中有 m 个点落入 M 中,则 M 的面积的估计值为 mnS ,假设正方形 ABCD 的边长为2, M 的面积为1,并向正方形 ABCD 中随机投掷 10000 个点,以 X 表示落入 M 中的点的数目.
(I)求 X 的均值 EX ;
(II)求用以上方法估计 M 的面积时, M 的面积的估计值与实际值之差在区间 (?0.03,0.03) 内的概率.
附表: P(k)=t=0kC10000t×0.25t×0.7510000?t
1.【答案】 A 2.【答案】 B 3.【答案】 D 4.【答案】 C 5.【答案】 A 6.【答案】 C 7.【答案】 C 8.【答案】 B 9.【答案】 C 10.【答案】 B
11.【答案】 0.38 12.【答案】 52
13.【答案】 解:如图,阴影部分是函数y= x 的图象与x轴和直线x=1围成的图形.设阴影部分的面积为S.
随机模拟的步骤:
⑴利用计算机产生两组[0,1]内的均匀随机数,x1=RAND,y1=RAND;
⑵统计试验总次数N和落在阴影内的点数N1(满足条件y< x x 的点(x,y)的个数);
⑶计算频率 N1N ,即为点落在阴影部分的概率的近似值;
⑷直线x=1,y=1和x,y轴围成的正方形面积是1,由几何概型公式得点落在阴影部分的概率为 s1 =S.
则S≈ N1N ,即阴影部分面积的近似值为 N1N .
14.【答案】 解: 我们通过设计模拟试验的方法来解决问题.利用计算机或计算器可以产生0到3之间取整数值的随机数.我们用0表示猜的选项正确,1,2,3表示猜的选项错误,这样可以体现猜对的概率是25%.因为共猜6道题,所以每6个随机数作为一组.例如,产生25组随机数:
330130 302220 133020 022011 313121 222330
231022 001003 213322 030032 100211 022210
231330 321202 031210 232111 210010 212020
230331 112000 102330 200313 303321 012033
321230
就相当于做了25次试验,在每组数中,如果恰有3个或3个以上的数是0,则表示至少答对3道题,它们分别是001003,030032,210010,112000,即共有4组数,我们得到该同学6道选择题至少答对3道题的概率近似为 425 =0.16.
15.【答案】 解:(I) EX=10000×14=2500 (II)依题意所求概率为 P(?0.03
10.3频率与概率
1.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率;先由计算器给出0到9之间取整数值的随机数,指定0、1、2、3表示没有击中目标, 4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数,根据以下数据估计该射击运动员射击4次至少击中3次的概率为(?? )
7527? 0293? 7140? 9857? 0347? 4373? 8636? 6947? 1417? 4698
0371? 6233? 2616? 8045? 6011? 3661? 9597? 7424? 7610? 4281
A.?0.4??????????????????????????????????????B.?0.45??????????????????????????????????????C.?0.5??????????????????????????????????????D.?0.55
2.已知P是△ABC所在平面内﹣点, PB+PC+2PA=0 ,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是(?? )
A.?23??????????????????????????????????????????B.?12??????????????????????????????????????????C.?13??????????????????????????????????????????D.?14
3.从区间[0,1]内随机抽取2n个数 x1 , x2 ,… xn , y1 ,.. , yn 构成n个数对( x1 , y1 ),…,( xn , yn ),其中两数的平方和不小于1的数对共有m个,则用随机模拟的方法得到圆周率π的近似值为(?? )
A.?mn????????????????????????????????????B.?4mn????????????????????????????????????C.?n?mn????????????????????????????????????D.?4(n?m)n
4.为了了解奥运五环及其内部所占面积与单独五个圆环及其内部面积之和的比值P , 某同学设计了如右图所示的数学模型,通过随机模拟的方法,在长为8,宽为5的矩形内随机取了 N 个点,经统计落入五环及其内部的点的个数为 n ,若圆环的半径为1,则比值 P 的近似值为(?? )
A.?32n5πN???????????????????????????????????B.?32nπN???????????????????????????????????C.?8nπN???????????????????????????????????D.?5n32πN
5.如图,在直角坐标系 xOy 中,过坐标原点 O 作曲线 y=ex 的切线,切点为 P ,过点 P 分别作 x,y 轴的垂线,垂足分别为 A,B ,向矩形 OAPB 中随机撒一粒黄豆,则它落到阴影部分的概率为(??? )
A.?e?22e?????????????????????????????????????B.?e?12e?????????????????????????????????????C.?e?2e?????????????????????????????????????D.?e?1e
6.哈六中数学兴趣小组的同学们为了计算六中数学组二维码中黑色部分的面积,在如图一个边长为 4 的正方形区域内随机投掷 400 个点,其中落入黑色部分的有 225 个点,据此可估计黑色部分的面积为(????? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.如图所示,分别以正方形ABCD两邻边AB、AD为直径向正方形内做两个半圆,交于点O.若向正方形内投掷一颗质地均匀的小球(小球落到每点的可能性均相同),则该球落在阴影部分的概率为( ??)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
8.分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域所示,若向该正方形内随机投一点,则该点落在阴影区域的概率为(?? )
A.?4?π2????????????????????????????????????B.?π?22????????????????????????????????????C.?4?π4????????????????????????????????????D.?π?24
9.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为5的正方形将其包含在内,并向该正方形内随机投掷1000个点,己知恰有400个点落在阴影部分,据此可估计阴影部分的面积是(?? )
A.?2??????????????????????????????????????????B.?3??????????????????????????????????????????C.?10??????????????????????????????????????????D.?15
10.下列关于用转盘进行随机模拟的说法中正确的是( ??)
A.?旋转的次数的多少不会影响估计的结果???????????????B.?旋转的次数越多,估计的结果越精确
C.?旋转时可以按规律旋转???????????????????????????????????????D.?转盘的半径越大,估计的结果越精确
11.如图,在平放的边长为1的正方形中随机撒1000粒豆子,有380粒落到红心阴影部分上,据此估计红心阴影部分的面积为________.
12.如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为400颗,以此实验数据为依据可以估计出该不规则图形的面积为________平方米.(用分数作答)
13.用随机模拟方法求函数 y=x ?与x轴和直线x=1围成的图形的面积.
14.一份测试题包括6道选择题,每题只有一个选项是正确的.如果一个学生对每一道题都随机猜一个答案,用随机模拟方法估计该学生至少答对3道题的概率.
15.如图,面积为 S 的正方形 ABCD 中有一个不规则的图形 M ,可按下面方法估计 M 的面积:在正方形 ABCD 中随机投掷 n 个点,若 n 个点中有 m 个点落入 M 中,则 M 的面积的估计值为 mnS ,假设正方形 ABCD 的边长为2, M 的面积为1,并向正方形 ABCD 中随机投掷 10000 个点,以 X 表示落入 M 中的点的数目.
(I)求 X 的均值 EX ;
(II)求用以上方法估计 M 的面积时, M 的面积的估计值与实际值之差在区间 (?0.03,0.03) 内的概率.
附表: P(k)=t=0kC10000t×0.25t×0.7510000?t
1.【答案】 A 2.【答案】 B 3.【答案】 D 4.【答案】 C 5.【答案】 A 6.【答案】 C 7.【答案】 C 8.【答案】 B 9.【答案】 C 10.【答案】 B
11.【答案】 0.38 12.【答案】 52
13.【答案】 解:如图,阴影部分是函数y= x 的图象与x轴和直线x=1围成的图形.设阴影部分的面积为S.
随机模拟的步骤:
⑴利用计算机产生两组[0,1]内的均匀随机数,x1=RAND,y1=RAND;
⑵统计试验总次数N和落在阴影内的点数N1(满足条件y< x x 的点(x,y)的个数);
⑶计算频率 N1N ,即为点落在阴影部分的概率的近似值;
⑷直线x=1,y=1和x,y轴围成的正方形面积是1,由几何概型公式得点落在阴影部分的概率为 s1 =S.
则S≈ N1N ,即阴影部分面积的近似值为 N1N .
14.【答案】 解: 我们通过设计模拟试验的方法来解决问题.利用计算机或计算器可以产生0到3之间取整数值的随机数.我们用0表示猜的选项正确,1,2,3表示猜的选项错误,这样可以体现猜对的概率是25%.因为共猜6道题,所以每6个随机数作为一组.例如,产生25组随机数:
330130 302220 133020 022011 313121 222330
231022 001003 213322 030032 100211 022210
231330 321202 031210 232111 210010 212020
230331 112000 102330 200313 303321 012033
321230
就相当于做了25次试验,在每组数中,如果恰有3个或3个以上的数是0,则表示至少答对3道题,它们分别是001003,030032,210010,112000,即共有4组数,我们得到该同学6道选择题至少答对3道题的概率近似为 425 =0.16.
15.【答案】 解:(I) EX=10000×14=2500 (II)依题意所求概率为 P(?0.03
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
